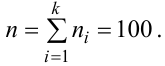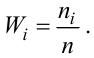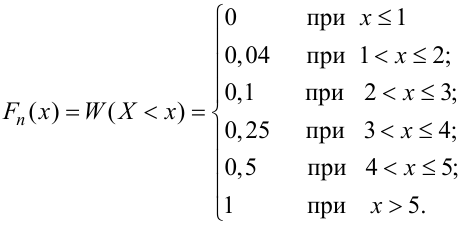Содержание:
- Числовые характеристики типичных законов распределения
- Биномиальный закон
- Закон Пуассона
- Геометрический закон
Дисперсия суммы случайных величин
Пусть 

Вычитая это равенство из предыдущего, получим:
где 

Найдем теперь дисперсию величины 

Число 
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Его называют ковариацией или корреляционным моментом случайных величин 

Формула (4.16) принимает теперь следующий вид:
– дисперсия суммы равна сумме дисперсий плюс удвоенная ковариация.
Ковариация или корреляционный момент, как свидетельствует его название (от латинского слова correlatio – соответствие, взаимосвязь), играет определенную роль при оценке зависимости 
Возможно вам будут полезны данные страницы:
Основное свойство ковариации выражается следующим предложением. Если величины 
Действительно, пусть 


Из доказанного предложения следует: если 

Из формулы (4.17) и доказанного выше свойства ковариации получаем важное следствие, носящее название теоремы сложения дисперсий для независимых случайных величин.
Теорема 4.3. Если величины 
Числовые характеристики типичных законов распределения
Теперь мы готовы к тому, чтобы найти математическое ожидание и дисперсию основных законов распределения: биномиального, пуассоновского и геометрического. Но прежде мы рассмотрим числовые характеристики простейшего закона распределения – индикатора случайного события
Пример с решением 4.4.
Пусть закон распределения случайной величины 
Найти математическое ожидание и дисперсию
Решение:
Очевидно, что 

Таким образом, для индикатора случайного события
Биномиальный закон
Пусть производится 








Непосредственное нахождение числовых характеристик в данном случае, используя закон распределения, является делом возможным, но затруднительным. Применим теорему сложения математических ожиданий и дисперсий для независимых величин. Для этого представим случайную величину 

Согласно примеру 4.4 математическое ожидание и дисперсия каждого слагаемого находится по формуле (4.18):
По теореме сложений математических ожиданий 

Окончательно имеем
Закон Пуассона
Закон Пуассона задается таблицей:
Отсюда имеем:
Таким образом, параметр 








Действительно, непосредственный подсчет дисперсии подтверждает это предположение, однако мы не приводим его здесь из-за сложности выкладок. Ниже мы выведем эти формулы более простым способом. Таким образом, для закона Пуассона
Геометрический закон
Напомним, что геометрический закон распределения связан с последовательностью испытаний Бернулли, которые проводятся до первого появления события 




Запишем выражение для математического ожидания
Ряд, записанный в скобках, получается почленным дифференцированием геометрической прогрессии
Следовательно,
Формула для дисперсии 
Пример с решением 4.5.
Проводится 160 независимых испытаний, в каждом из которых подбрасывается 5 монет. Пусть 
Решение:
Очевидно, что величина 
Согласно формуле (4.19)
Пример с решением 4.6.
В спортивной лотерее каждую неделю на 100 билетов разыгрывается 5 палаток и 5 рюкзаков. Турист решил каждую неделю покупать по одному билету до тех пор, пока он не выиграет палатку и рюкзак. Найти среднее время (в неделях) реализации этого намерения.
Решение:
Обозначим через 








Пример с решением 4.7.
Игральная кость подбрасывается до тех пор, пока не выпадут все грани. Найти математическое ожидание и дисперсию числа бросаний.
Решение:
Случайная величина 
Здесь 



Применяя теорему сложения для математических ожиданий и дисперсий, а также формулы 6
(4.21), имеем
Лекции:
- Дисперсия формула
- Математическое ожидание: пример решения
- Законы распределения случайных величин
- Моменты случайной величины
- Моменты высших порядков
- Мат ожидание: примеры с решением
- Непрерывные случайные величины примеры с решением
- Числовые характеристики непрерывной случайной величины
- Функция случайной величины
- Математическая дисперсия случайной величины
Дисперсия и ее свойства.
Среднее квадратическое отклонение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дисперсия и формула для ее вычисления
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией называется
математическое ожидание квадрата отклонения случайной величины
от
:
Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:
Свойства дисперсии
Свойство 1.
Дисперсия равна разности между
математическим ожиданием квадрата случайной величины
и
квадратом ее математического ожидания.
Свойство 2.
Дисперсия константы
равна нулю:
Свойство 3.
Постоянный множитель
выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы
случайных величин:
где
–
ковариация случайных величин
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Следствия из свойств дисперсии.
В частности, если
и
независимы, то
Прибавление константы
в
случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
Среднеквадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Стандартное (среднее
квадратичное) отклонение случайной величины
определяется
как корень из дисперсии и обозначается
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X – в квадратных метрах.
Смежные темы решебника:
- Математическое ожидание и его свойства
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число конфет с вареньем, может принимать
значения 0,1,2
Найдем
соответствующие вероятности:
Проверка:
Получаем
следующий закон распределения СВ
:
Математическое
ожидание:
Дисперсию
можно вычислить по формуле:
Искомая
дисперсия:
Пример 2
Даны
законы распределения независимых случайных величин X и Y:
и
Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение суммы
:
Окончательно получаем:
|
|
2 | 3 | 4 | Итого |
|
|
0.2 | 0.5 | 0.3 | 1 |
Вычислим математические ожидания:
Вычислим
дисперсии:
Проверим
равенство
:
Равенство
выполняется.
Пример 3
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
Решение
Математическое
ожидание биномиального распределения:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 1-м станке:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 2-м станке:
Дисперсия:
Математическое
ожидание числа бракованных деталей:
Дисперсия
числа бракованных деталей:
Ответ:
;
.
Пример 4
Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)2}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку
случайные величины
и
распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:
Пользуясь
свойствами математического ожидания и дисперсии:
Подставляя
числовые значения, получаем:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Независимые случайные величины X и Y
заданы следующими законами:
| x | 2.3 | 2.5 | 2.7 | 2.9 |
| p | 0.4 | 0.3 | 0.2 | 0.1 |
Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.
Задача 2
Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.
| x | -5 | 2 | 3 | 4 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
Написать F(x) и построить ее график.
Задача 3
Случайная
величина X имеет плотность вероятности
Требуется
найти дисперсию Dx.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.
Задача 5
Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Задача 6
Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
Задача 7
Дискретная
случайная величина X имеет только два возможных значения: x1 и x2, причем x2>x1. Вероятность того, что X
примет значение x1, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
Задача 8
Закон
распределения случайной величины ξ имеет вид:
| ξ | -1 | 2 | 3 | 5 |
| P | 1/4 | 1/2 | 1/8 | 1/8 |
Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.
Задача 9
Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.
Задача 10
Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности
при
и
в остальных точках.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
-
Дисперсия суммы случайных величин. Корреляционный момент.
Пусть
и
случайные величины.
Рассмотрим их сумму.
Математическое ожидание этой суммы
будет равно сумме математических
ожиданий.
Найдем дисперсию суммы случайных величин
Вычтем из первого уравнения второе и
возведем в квадрат.
Для сокращения записи введем обозначения:
Тогда,
Величину
принято обозначать
и называть корреляционным моментом,
или моментом связи случайных величини
.
Тогда дисперсии суммы равна сумме
дисперсий плюс удвоенный корреляционный
момент.
Основное свойство корреляционного
момента.
Если величины
и
независимы, то их корреляционный момент
равен нулю.
Обратное утверждение неверно.
-
Теорема сложения дисперсий.
Из последнего свойства следует, что
если величины
и
независимы, то дисперсия их суммы
равна сумме их дисперсий.
.
Этой теоремой широко пользуются в теории
погрешностей при обработке результатов
косвенных измерений, так как входящие
в расчетные формулы величины в большинстве
случаев являются независимыми, и поэтому
подсчитывая среднеквадратичную
погрешность вы суммируете квадраты
всех погрешностей.
-
Коэффициент корреляции.
Полученный выше корреляционный момент
зависит от выбора единиц измерения
и
.Это затрудняет сравнение
корреляционных моментов различных
случайных величин. Поэтому удобнее
пользоваться безразмерной величинойкоэффициентом
корреляции:
где
среднеквадратичные
отклонения случайных величин
и
.
Без доказательства дадим следующие
свойства коэффициента корреляции:
-
Коэффициент корреляции
;
-
Если
близко к 1, зависимость между
и
близка к линейной; если
,
то корреляция положительна, еслиотрицательная.
-
Когда
,
величины
и
связаны функциональной линейной
зависимостью.
-
Оценка значимости коэффициента корреляции.
При проведении корреляционного анализа
часто возникает вопрос, являются ли
полученные из наблюдений коэффициенты
значимыми и не объясняется ли их появление
случайным характером выборки.
Фактически, полученный коэффициент
корреляции всегда является выборочным,
так как он вычисляется на основе
ограниченной совокупности, представляющей
выборку из генеральной. Поэтому он имеет
ошибку выборочности, которая является
мерой расхождения между
и коэффициентом корреляции для
генеральной совокупности.
Определив среднюю ошибку, можно
судить о степени достоверности.
Принимается нулевая гипотеза, согласно
которой
,
то есть считается, что в генеральной
совокупности нет корреляции между
варьирующими признаками. Тогда критерий
Стьюдента рассчитывается по
формуле:
Если выборка достаточно велика
,
то
Т.к. распределение
при малых
выборках
может значительно отличаться от
нормального, для расчета критерия
Стьюдента пользуются формулой:
Если найденное значение превышает
табличное
для заданного уровня значимости и числа
степеней свободы,
можно считать нулевую гипотезу
отвергнутой, т.е. признать данное значениедостоверным. Если же
,
то нулевая гипотеза принимается и
найденный коэффициент корреляции нельзя
считать достоверным, т.е. корреляции
между варьирующими признаками нет.
-
Измерение связи. Регрессия.
-
Понятие о регрессии. Уравнение регрессии.
-
Коэффициент корреляции указывает лишь
на степень связи в вариации двух
переменных величин, но не дает
возможности судить о том, как количественно
меняется одна величина по мере изменения
другой. На этот вопрос отвечает метод
регрессии. Регрессия может быть
двусторонней: определение изменения
по изменению
,
и определение измененияпо изменению
.
Эмпирическая линия регрессии обычно
представляет собой ломаную линию. Если
в силу каких-либо причин мы можем
предположить, что исследуемая зависимость
является линейной, то мы можем заменить
ломаную линию прямой. Уравнение прямой
линии имеет вид:
Задача состоит в определении
коэффициентов регрессииВ общем случае они определяют наклон
прямой линии и пересечение с осью У.
Для двусторонней регрессии следует
различать
Коэффициент
можно найти по известным значениям
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 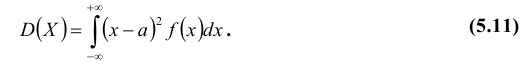
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
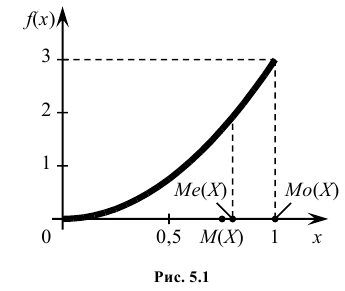
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 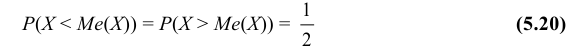
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 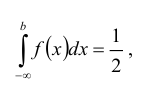
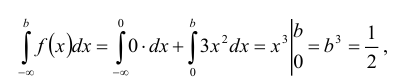
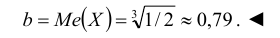
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 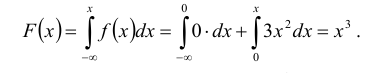
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
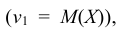
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 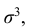
Полученная величина А называется коэффициентом асимметрии случайной величины: 
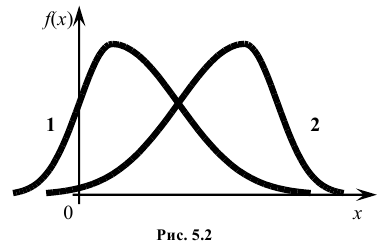
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
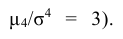
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 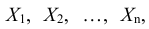
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 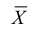
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
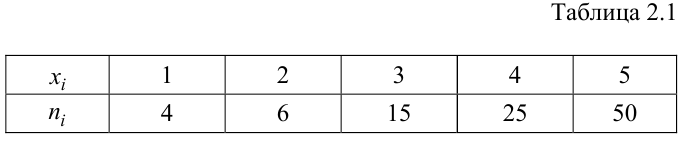
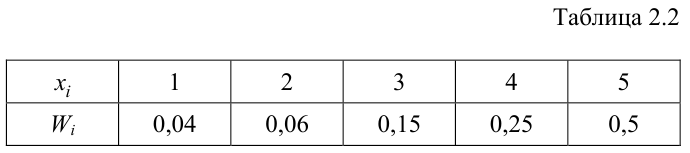
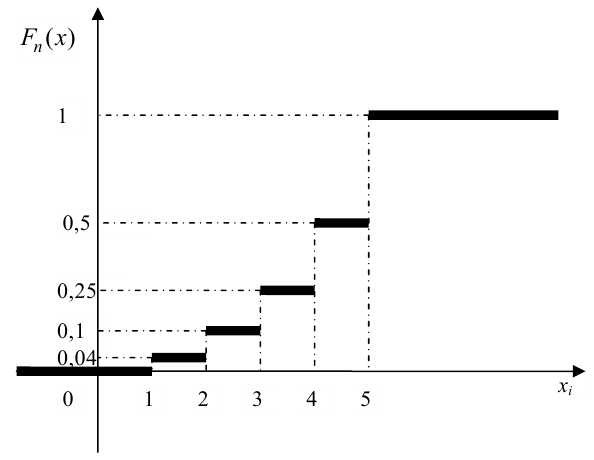
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 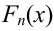
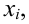
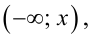
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение
- Закон распределения дискретной случайной величины
- Математическое ожидание
- Дисперсия
- Среднее квадратичное отклонение
- Правило трёх сигм
- Примеры
п.1. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют соответствие между полученными на опыте значениями этой величины X= {xi} и их вероятностями pi = P(xi).
При этом сумма всех вероятностей равна 1: (mathrm{sum_{i=1}^n p_i=1})
Закон распределения можно задать таблицей, графиком или аналитически (в виде формулы).
Например:
Закон распределения случайной величины X = {0;1;2;3}, равной числу выпадения орлов при 3 бросках монеты, аналитически задаётся формулой: $$ mathrm{ p_i=P(x_i)=P_3(i)=frac{C_3^{i}}{2^3}, i={0;1;2;3} } $$
В табличном виде:
|
xi |
pi |
|
0 |
1/8 |
|
1 |
3/8 |
|
2 |
3/8 |
|
3 |
1/8 |
В виде графика:
п.2. Математическое ожидание
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ mathrm{ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} } $$ Математическое ожидание является средним значением величины X.
Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
M(C) = C
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
M(X + Y) = M(X) + M(Y)
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
M(XY) = M(X) · M(Y)
6) Постоянный множитель можно вынести за знак математического ожидания:
M(CX) = C · M(X)
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):
| Число белых шаров, xi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | (mathrm{C_5^0q^5}) | (mathrm{C_5^1pq^4}) | (mathrm{C_5^2p^2q^3}) | (mathrm{C_5^3p^3q^2}) | (mathrm{C_5^4p^4q}) | (mathrm{C_5^5p^5}) |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Найдём математическое ожидание для данного распределения:
M(X) = 0 · 0,0074 + 1 · 0,0618 + … + 5 · 0,0954 = 3,125
п.3. Дисперсия
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ mathrm{ D(X)=M(X-M(X))^2 } $$ На практике дисперсия рассчитывается по формуле: $$ mathrm{ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) } $$
Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
D(C) = 0
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
D(X + Y) = D(X) + D(Y)
5) Постоянный множитель можно вынести за знак дисперсии:
D(CX) = C2 · D(X)
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
pi
0,0074
0,0618
0,2060
0,3433
0,2861
0,0954
1
xip1
0
0,0618
0,4120
1,0300
1,1444
0,4768
3,125
(mathrm{x_i^2})
0
1
4
9
16
25
–
(mathrm{x_i^2p_i})
0
0,0618
0,8240
3,0899
4,5776
2,3842
10,9375
Получаем: D(X) = 10,9375 – 3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ mathrm{ sigma(X)=sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
σ(C) = 0
4) Постоянный множитель можно вынести за знак СКО:
σ(CX) = C · σ(X)
п.5. Правило трёх сигм
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и (mathrm{sigma(X)=sqrt{npq}}).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
pi
1/6
1/6
1/6
1/6
1/6
1/6
1
xip1
1/6
1/3
1/2
2/3
5/6
1
3,5
(mathrm{x_i^2})
1
4
9
16
25
36
–
(mathrm{x_i^2p_i})
(mathrm{frac16})
(mathrm{frac23})
(mathrm{1frac12})
(mathrm{2frac23})
(mathrm{4frac16})
6
(mathrm{15frac16})
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=1}^6 x_ip_i=3,5 }\ mathrm{ D(X)=sum_{i=1}^6 x_i^2p_i-M^2(X)=15frac16-3,5^3=2frac{11}{12} }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{2frac{11}{12}}approx 1,7 } end{gather*} Ответ: (mathrm{M(X)=3,5; D(X)=2frac{11}{12}; sigma(X)approx 1,7}).
Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.
Используем свойства мат.ожиданий и дисперсий.
Пусть X – очки на первом кубике, Y – на втором.
Параметры распределения для каждого из кубиков рассчитаны в примере 1.
(mathrm{M(X)=M(Y)=3,5, D(X)=D(Y)=2frac{11}{12}}).
Для суммы очков получаем:
(mathrm{M(X+Y)=M(X)+M(Y)=3,5+3,5=7})
(mathrm{D(X+Y)=D(X)+D(Y)=2frac{11}{12}+2frac{11}{12}=5frac56})
(mathrm{sigma(X+Y)=sqrt{D(X+Y)}=sqrt{5frac56}approx 2,4})
Ответ: (mathrm{M(X+Y)=7; D(X+Y)=5frac56; sigma(X+Y)approx 2,4}).
Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.
Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:
(mathrm{x_i^2p_i})
0
p
p
Мат.ожидание первого опыта (mathrm{M(X)=sum x_ip_i=p}).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (mathrm{X=X_1+X_2+…+X_n}). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: begin{gather*} mathrm{ M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)= }\ mathrm{=underbrace{p+p+…+p}_{n text{раз}}=np } end{gather*} Дисперсия первого опыта (mathrm{D(X)=sum x_i^2p_i-M(X)=p-p^2=p(1-p)=pq})
По свойству дисперсии суммы независимых событий: begin{gather*} mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\ mathrm{=underbrace{pq+pq+…+pq}_{n text{раз}}=npq } end{gather*} Что и требовалось доказать.
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. begin{gather*} mathrm{ M(X)=np=100cdot 0,4=40 }\ mathrm{D(X)=npq=100cdot 0,4cdot 0,6=24 }\ mathrm{sigma(X)=sqrt{D(X)}=sqrt{24}approx 4,9} end{gather*} Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X)lt Xlt M(X)+3sigma(X) }\ mathrm{40-3cdot 4,9lt Xlt 40+3cdot 4,9 }\ mathrm{25,3lt Xlt 54,7}\ mathrm{26leq Xleq 54} end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: (mathrm{M(X)=40; D(X)=24; sigma(X)approx 4,9; 26leq Xleq 54})
Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?
По условию: (mathrm{n=10, p=frac14, q=frac34}).
Для каждого ответа может быть два исхода: «угадал»/ «не угадал».
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. $$ mathrm{ P_{10}(k)=C_{10}^kp^kq^{10-k}=C_{10}^kfrac{3^{10-k}}{4^{10}}=left(frac34right)^{10}frac{C_{10}^k}{3^k} } $$ Строим расчётную таблицу. Для (mathrm{C_{10}^k}) используем рекуррентную формулу (см. §36 данного справочника): $$ mathrm{ C_{n}^k=frac{n-k+1}{k}C_n^{k-1} } $$
| (mathrm{x_i=k}) | (mathrm{C_k}) | (mathrm{3^k}) | (mathrm{p_i(x_i)}) | (mathrm{x_icdot p_i}) | (mathrm{x_i^2}) | (mathrm{x_i^2cdot p_i}) |
| 0 | 1 | 1 | 0,0563135 | 0,0000000 | 0 | 0,0000000 |
| 1 | 10 | 3 | 0,1877117 | 0,1877117 | 1 | 0,1877117 |
| 2 | 45 | 9 | 0,2815676 | 0,5631351 | 4 | 1,1262703 |
| 3 | 120 | 27 | 0,2502823 | 0,7508469 | 9 | 2,2525406 |
| 4 | 210 | 81 | 0,1459980 | 0,5839920 | 16 | 2,3359680 |
| 5 | 252 | 243 | 0,0583992 | 0,2919960 | 25 | 1,4599800 |
| 6 | 210 | 729 | 0,0162220 | 0,0973320 | 36 | 0,5839920 |
| 7 | 120 | 2187 | 0,0030899 | 0,0216293 | 49 | 0,1514053 |
| 8 | 45 | 6561 | 0,0003862 | 0,0030899 | 64 | 0,0247192 |
| 9 | 10 | 19683 | 0,0000286 | 0,0002575 | 81 | 0,0023174 |
| 10 | 1 | 59049 | 0,0000010 | 0,0000095 | 100 | 0,0000954 |
| Σ | 1 | 2,5 | 8,125 |
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=0}^{10} x_ip_i=2,5 }\ mathrm{ D(X)=sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{1,875}approx 1,37 } end{gather*}
Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X) lt Xlt M(X)+3sigma(X) }\ mathrm{ 2,5-3cdot 1,37lt X lt 2,5+3cdot 1,37 }\ mathrm{ -1,61lt Xlt 6,61 }\ mathrm{ 0leq Xleq 6 } end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.
Вероятность угадать хотя бы один ответ: begin{gather*} mathrm{ P(Xgeq 1)=1-p_0approx 1-0,0563=0,9437 }end{gather*} Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: begin{gather*} mathrm{ P(Xgeq 5)=1-left(sum_{i=0}^{4}{p_i} right)approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.





































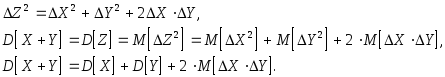



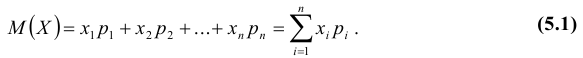
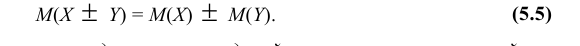


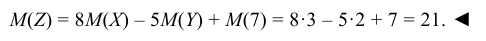







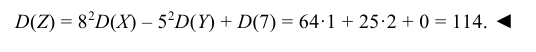
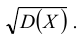

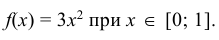




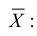
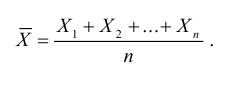

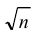 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: