Как найти дисперсию в r studio

Как найти дисперсию в r studio

Благодаря наличию специально созданных для этого функций, расчет параметров описательной статистики в R не составляет никакого труда. Ниже я продемонстрирую использование этих функций на примере ранее рассмотренных данных по характеристикам 32 моделей автомобилей (таблица mtcars, входящая в стандартный набор данных R):

data(mtcars)
mtcars
                     mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Mazda RX4           21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag       21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
Datsun 710          22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive      21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout   18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Valiant             18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
Duster 360          14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
Merc 240D           24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
Merc 230            22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
Merc 280            19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
...
...

Каждая модель описана по 11 признакам, два из которых (vs и am) являются номинальными переменными (факторами) c уровнями, закодированными в виде 0 и 1 (подробнее см. ?mtcars).

Для расчета  арифметической средней, медианы, дисперсии, стандартного отклонения, а также минимального и максимального значений в R служат функции mean(), median(), var(), sd(), min() и max() соответственно. Используем эти функции в отношении, например, параметра mpg (пробег автомобиля (в милях) в расчете на один галлон топлива):

# Минимальное значение:
min(mtcars$mpg)
[1] 10.4
 
# Максимальное значение:
max(mtcars$mpg)
[1] 33.9

Специальной функции для расчета стандартной ошибки средней в R нет, однако для этого вполне подойдут уже имеющиеся функции. Как известно, стандартная ошибка средней рассчитывается как отношение стандартного отклонения к квадратному корню из объема выборки:
[S_{bar{x}} = frac{S}{sqrt{n}}]

На языке R мы можем записать это следующим образом:

SEmpg = sd(mtcars$mpg)/sqrt(length(mtcars$mpg))
# функция length() возвращает число элементов в векторе mpg

Получаем:

Квантили рассчитываются в R при помощи функции quantile():

quantile(mtcars$mpg)
    0%    25%    50%    75%   100% 
10.400 15.425 19.200 22.800 33.900

При настройках, заданных по умолчанию, выполнение указанной команды приведет к расчету минимального (10.4) и максимального (33.9) значений, а также трех квартилей, т.е. значений, которые делят совокупность на четыре равные части – 15.4, 19.2 и 22.8. Разница между первым и третим квартилями носит название интерквартильный размах (ИКР; англ. interquartile range). ИКР является робастным аналогом дисперсии и может быть рассчитан в R при помощи функции IQR():

Функция quantile() позволяет рассчитать и другие квантили. Например, децили (т.е. значения, делящие совокупность на десять частей) можно получить следующим образом:

quantile(mtcars$mpg, p = seq(0, 1, 0.1))
   0%   10%   20%   30%   40%   50%   60%   70%   80%   90%  100% 
10.40 14.34 15.20 15.98 17.92 19.20 21.00 21.47 24.08 30.09 33.90

В приведенной команде важен аргумент p (от probability – вероятность), при помощи которого был задан вектор чисел от 0 до 1 с шагом 0.1.

Обратите внимание на то, что существует несколько способов оценки квантилей по выборочным данным. Подробнее об этом можно узнать в справочном файле по функции quantile() (доступен по команде ?quantile).

Отсутствующие значения в данных могут несколько усложнить вычисления. В качестве демонстрации заменим 3-е значение переменной mpg на NA (от not available – не доступно) – обозначение, используемое в R для отсутствующих наблюдений, – а затем попытаемся вычислить среднее значение:

mtcars$mpg[3] <- NA
 
# Просмотрим результат:
head(mtcars$mpg)
[1] 21.0 21.0   NA 21.4 18.7 18.1
 
# Попробуем рассчитать среднее значение для mpg:
mean(mtcars$mpg)
[1] NA

Ничего не вышло – вместо среднего значения программа выдала NA, что вполне логично. R не будет пропускать отсутствующие значения автоматически, если мы не включим соответствующую опцию – na.rm (от not available и remove – удалить):

Рассмотренный прием срабатывает в большинстве случаев. Одним из немногих исключений является функция length(), используемая для определения размера вектора. Аргумент na.rm у этой функции отсутствует, так что подсчитаны будут и имеющиеся, и отсутствующие значения:

Если все же стоит задача подсчитать количество неотсутствующих значений, то можно воспользоваться следующим приемом:

Ключом здесь является использование команды is.na(mtcars$mpg), которая проверяет каждое значение mpg и возвращает FALSE, если это значение не равно NA, и TRUE иначе. В сочетании с логическим оператором ! (“не”), команда sum далее подсчитывает только те значения mpg, которые не равны NA (логические TRUE здесь конвертируются в 1, которые можно суммировать).

Существуют еще две функции, которые могут оказаться полезными при анализе свойств совокупностей – which.min() и which.max(). Как следует из названий, эти функции позволяют выяснить порядковые номера элементов, обладающих минимальным и максимальным значениями соответственно. Если минимальное/максимальное значение принимают несколько элементов в векторе, то будет возвращен порядковый номер первого элемента с этим значением. В случае с mpg имеем:

Видим, что минимальный и максимальный пробег в расчете на галлон топлива имеют модели под номерами 15 и 20 соответственно. Выяснить названия этих моделей мы можем, совместив команды which.min() и which.max() с командой rownames() (от row – строка, и

names

– имена):

Подробнее о приемах индексирования векторов в R см. здесь.

Использование функции summary()

В системе R имеется возможность и более быстрого расчета основных параметров описательной статистики. Для этого, в частности, служит функция общего назначения summary():

summary(mtcars$mpg)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
  10.40   15.35   19.20   20.00   22.15   33.90    1.00

Всего одной строки кода оказалось достаточно для получения минимального (Min) и максимального (Max) значений переменной mpg, медианы (Median), арифметической средней (Mean), первого (1st Qu.) и третьего (3rd Qu.) квартилей, а также для выяснения количества отсутствующих значений (NA’s). Более того, подобную сводку мы можем получить сразу для всей таблицы данных:

summary(mtcars)
      mpg             cyl             disp             hp       
 Min.   :10.40   Min.   :4.000   Min.   : 71.1   Min.   : 52.0  
 1st Qu.:15.35   1st Qu.:4.000   1st Qu.:120.8   1st Qu.: 96.5  
 Median :19.20   Median :6.000   Median :196.3   Median :123.0  
 Mean   :20.00   Mean   :6.188   Mean   :230.7   Mean   :146.7  
 3rd Qu.:22.15   3rd Qu.:8.000   3rd Qu.:326.0   3rd Qu.:180.0  
 Max.   :33.90   Max.   :8.000   Max.   :472.0   Max.   :335.0  
 NA's   : 1.00                                                  
      drat             wt             qsec             vs        
 Min.   :2.760   Min.   :1.513   Min.   :14.50   Min.   :0.0000  
 1st Qu.:3.080   1st Qu.:2.581   1st Qu.:16.89   1st Qu.:0.0000  
 Median :3.695   Median :3.325   Median :17.71   Median :0.0000  
 Mean   :3.597   Mean   :3.217   Mean   :17.85   Mean   :0.4375  
 3rd Qu.:3.920   3rd Qu.:3.610   3rd Qu.:18.90   3rd Qu.:1.0000  
 Max.   :4.930   Max.   :5.424   Max.   :22.90   Max.   :1.0000  
 
       am              gear            carb      
 Min.   :0.0000   Min.   :3.000   Min.   :1.000  
 1st Qu.:0.0000   1st Qu.:3.000   1st Qu.:2.000  
 Median :0.0000   Median :4.000   Median :2.000  
 Mean   :0.4062   Mean   :3.688   Mean   :2.812  
 3rd Qu.:1.0000   3rd Qu.:4.000   3rd Qu.:4.000  
 Max.   :1.0000   Max.   :5.000   Max.   :8.000

Результат выглядел бы замечательно, если бы не одно “но”. Переменные vs и am являются факторами, но уровни их закодированы при помощи чисел 0 и 1. К сожалению, система R не распознала эти две переменные как факторы и рассчитала соответствующие параметры описательной статистики, как для обычных числовых переменных. Однако мы можем изменить такое поведение R, самостоятельно преобразовав vs и am в факторы при помощи функции as.factor():

Теперь результат действия функции summary() в отношении таблицы mtcars будет выглядеть так:

summary(mtcars)
      mpg             cyl             disp             hp       
 Min.   :10.40   Min.   :4.000   Min.   : 71.1   Min.   : 52.0  
 1st Qu.:15.35   1st Qu.:4.000   1st Qu.:120.8   1st Qu.: 96.5  
 Median :19.20   Median :6.000   Median :196.3   Median :123.0  
 Mean   :20.00   Mean   :6.188   Mean   :230.7   Mean   :146.7  
 3rd Qu.:22.15   3rd Qu.:8.000   3rd Qu.:326.0   3rd Qu.:180.0  
 Max.   :33.90   Max.   :8.000   Max.   :472.0   Max.   :335.0  
 NA's   : 1.00
      drat             wt             qsec       vs     am    
 Min.   :2.760   Min.   :1.513   Min.   :14.50   0:18   0:19  
 1st Qu.:3.080   1st Qu.:2.581   1st Qu.:16.89   1:14   1:13  
 Median :3.695   Median :3.325   Median :17.71                
 Mean   :3.597   Mean   :3.217   Mean   :17.85                
 3rd Qu.:3.920   3rd Qu.:3.610   3rd Qu.:18.90                
 Max.   :4.930   Max.   :5.424   Max.   :22.90                
 
      gear            carb      
 Min.   :3.000   Min.   :1.000  
 1st Qu.:3.000   1st Qu.:2.000  
 Median :4.000   Median :2.000  
 Mean   :3.688   Mean   :2.812

Обратите внимание на сводки по vs и am: поскольку эти переменные теперь распознаны программой как факторы, единственный способ описать их – это подсчитать количество наблюдений для каждого уровня.

Использование функции tapply()

Функция tapply() принадлежит к важному “apply-семейству” R-функций. Эти функции позволяют выполнять математические вычисления над определенными элементами таблиц данных, матриц, или массивов (например, быстро вычислять среднее значение для каждого столбца или строки таблицы, и т.п.).

Предположим, мы хотим выяснить средний объем двигателя (переменная disp, в кубических дюймах) у моделей с автоматической и ручной коробкой передач (переменная am; 1 – ручная коробка, 0 – автоматическая коробка). Функция tapply() позволяет сделать это следующим образом:

Как видно из приведенной команды, основными аргументами функции tapply() являются:

  • Х – числовой вектор
  • INDEX – список факторов, для уровней которых рассчитываются значения функции FUN
  • FUN – любая, в том числе пользовательская, функция

Поскольку аргумент INDEX способен принимать список из нескольких факторов, мы можем усложнить приведенную выше команду:

Аргумент FUN, как уже было отмечено, может принимать любые, в том числе и пользовательские функции. Рассмотрим, например, расчет стандартных ошибок для средних значений объема двигателя у автомобилей с автоматической и ручной коробкой передач. Для начала создадим функцию SE для расчета стандартных ошибок (см. пример выше):

Теперь совместим эту новую функцию с tapply():

Таким образом, объем двигателя у моделей с автоматической коробкой передач составляет в среднем 290.4 ± 25.3, а у автомобилей с механической коробкой – 143.5 ± 24.2 кубических дюймов.

Использование дополнительных пакетов

Рассмотренные выше функции позволяют получить достаточно полное представление об анализируемых выборках и таблицах данных. Однако специальные функции для расчета некоторых параметров описательной статистики не входят в базовую версию R. С одним из таких параметров мы уже столкнулись – стандартная ошибка арифметической средней. Другие примеры включают коэффициенты эксцесса (англ. kurtosis) и асимметрии (skewness) – параметры, характеризующие форму распределения. Конечно, мы можем рассчитать эти величины по соответствующим формулам или даже написать собственные функции для этих целей. Однако это уже было сделано до нас – достаточно воспользоваться имеющимися дополнительными пакетами для R, например, пакетом moments. Если этот пакет не установлен на Вашем компьютере, выполните следующую команду (естественно, Ваш компьютер должен быть при этом подключен к Internet):

Рассчитать коэффициенты эксцесса и асимметрии теперь очень просто:

Многие R-пакеты имеют собственные функции, аналогичные стандартной summary(), для вывода компактных описательных сводок по таблицам данных. Ниже приведены несколько примеров таких пакетов и функций (предполагается, что соответствующий пакет уже установлен на Вашем копьютере и загружен в рабочее пространство R; подробности вывода результатов анализа здесь не обсуждаются – см. справочные материалы по соответствующим командам).

# Пакет Hmisc, функция describe():
 
describe(mtcars)
mtcars 
 
 11  Variables      32  Observations
--------------------------------------------------------------------------------------------
mpg 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     31       1      25      20   11.85   14.30   15.35   19.20   22.15   30.40   31.40 
 
lowest : 10.4 13.3 14.3 14.7 15.0, highest: 26.0 27.3 30.4 32.4 33.9 
--------------------------------------------------------------------------------------------
cyl 
      n missing  unique    Mean 
     32       0       3   6.188 
 
4 (11, 34%), 6 (7, 22%), 8 (14, 44%) 
--------------------------------------------------------------------------------------------
disp 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     32       0      27   230.7   77.35   80.61  120.83  196.30  326.00  396.00  449.00 
 
lowest :  71.1  75.7  78.7  79.0  95.1, highest: 360.0 400.0 440.0 460.0 472.0 
--------------------------------------------------------------------------------------------
hp 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     32       0      22   146.7   63.65   66.00   96.50  123.00  180.00  243.50  253.55 
 
lowest :  52  62  65  66  91, highest: 215 230 245 264 335 
--------------------------------------------------------------------------------------------
drat 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     32       0      22   3.597   2.853   3.007   3.080   3.695   3.920   4.209   4.314 
 
lowest : 2.76 2.93 3.00 3.07 3.08, highest: 4.08 4.11 4.22 4.43 4.93 
--------------------------------------------------------------------------------------------
wt 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     32       0      29   3.217   1.736   1.956   2.581   3.325   3.610   4.048   5.293 
 
lowest : 1.513 1.615 1.835 1.935 2.140, highest: 3.845 4.070 5.250 5.345 5.424 
--------------------------------------------------------------------------------------------
qsec 
      n missing  unique    Mean     .05     .10     .25     .50     .75     .90     .95 
     32       0      30   17.85   15.05   15.53   16.89   17.71   18.90   19.99   20.10 
 
lowest : 14.50 14.60 15.41 15.50 15.84, highest: 19.90 20.00 20.01 20.22 22.90 
--------------------------------------------------------------------------------------------
vs 
      n missing  unique 
     32       0       2 
 
0 (18, 56%), 1 (14, 44%) 
--------------------------------------------------------------------------------------------
am 
      n missing  unique 
     32       0       2 
 
0 (19, 59%), 1 (13, 41%) 
--------------------------------------------------------------------------------------------
gear 
      n missing  unique    Mean 
     32       0       3   3.688 
 
3 (15, 47%), 4 (12, 38%), 5 (5, 16%) 
--------------------------------------------------------------------------------------------
carb 
      n missing  unique    Mean 
     32       0       6   2.812 
 
           1  2 3  4 6 8
Frequency  7 10 3 10 1 1
%         22 31 9 31 3 3
--------------------------------------------------------------------------------------------
# Пакет pastecs, функция stat.desc()
 
stat.desc(mtcars) 
                mpg    cyl    disp      hp    drat     wt   qsec
nbr.val       31.00  32.00 3.2e+01   32.00  32.000  32.00  32.00
nbr.null       0.00   0.00 0.0e+00    0.00   0.000   0.00   0.00
nbr.na         1.00   0.00 0.0e+00    0.00   0.000   0.00   0.00
min           10.40   4.00 7.1e+01   52.00   2.760   1.51  14.50
max           33.90   8.00 4.7e+02  335.00   4.930   5.42  22.90
range         23.50   4.00 4.0e+02  283.00   2.170   3.91   8.40
sum          620.10 198.00 7.4e+03 4694.00 115.090 102.95 571.16
median        19.20   6.00 2.0e+02  123.00   3.695   3.33  17.71
mean          20.00   6.19 2.3e+02  146.69   3.597   3.22  17.85
SE.mean        1.10   0.32 2.2e+01   12.12   0.095   0.17   0.32
CI.mean.0.95   2.24   0.64 4.5e+01   24.72   0.193   0.35   0.64
var           37.28   3.19 1.5e+04 4700.87   0.286   0.96   3.19
std.dev        6.11   1.79 1.2e+02   68.56   0.535   0.98   1.79
coef.var       0.31   0.29 5.4e-01    0.47   0.149   0.30   0.10
             vs am   gear  carb
nbr.val      NA NA  32.00 32.00
nbr.null     NA NA   0.00  0.00
nbr.na       NA NA   0.00  0.00
min          NA NA   3.00  1.00
max          NA NA   5.00  8.00
range        NA NA   2.00  7.00
sum          NA NA 118.00 90.00
median       NA NA   4.00  2.00
mean         NA NA   3.69  2.81
SE.mean      NA NA   0.13  0.29
CI.mean.0.95 NA NA   0.27  0.58
var          NA NA   0.54  2.61
std.dev      NA NA   0.74  1.62
coef.var     NA NA   0.20  0.57
# Пакет psych, функция describe()
 
describe(mtcars)
     var  n  mean     sd median trimmed    mad  min   max range
mpg    1 31  20.0   6.11   19.2    19.6   5.49 10.4  33.9  23.5
cyl    2 32   6.2   1.79    6.0     6.2   2.97  4.0   8.0   4.0
disp   3 32 230.7 123.94  196.3   222.5 140.48 71.1 472.0 400.9
hp     4 32 146.7  68.56  123.0   141.2  77.10 52.0 335.0 283.0
drat   5 32   3.6   0.53    3.7     3.6   0.70  2.8   4.9   2.2
wt     6 32   3.2   0.98    3.3     3.1   0.77  1.5   5.4   3.9
qsec   7 32  17.9   1.79   17.7    17.8   1.42 14.5  22.9   8.4
vs*    8 32   1.4   0.50    1.0     1.4   0.00  1.0   2.0   1.0
am*    9 32   1.4   0.50    1.0     1.4   0.00  1.0   2.0   1.0
gear  10 32   3.7   0.74    4.0     3.6   1.48  3.0   5.0   2.0
carb  11 32   2.8   1.62    2.0     2.6   1.48  1.0   8.0   7.0
      skew kurtosis    se
mpg   0.64    -0.03  1.10
cyl  -0.17    -1.76  0.32
disp  0.38    -1.07 21.91
hp    0.73     0.28 12.12
drat  0.27    -0.45  0.09
wt    0.42     0.42  0.17
qsec  0.37     0.86  0.32
vs*   0.24    -2.06  0.09
am*   0.36    -1.97  0.09
gear  0.53    -0.90  0.13
carb  1.05     2.02  0.29
# Пакет psych, функция describe.by() - расчет параметров описательной статистики
# для каждого уровня некоторого фактора:
 
describe.by(mtcars, mtcars$am)
group: 0
     var  n  mean     sd median trimmed    mad   min   max range
mpg    1 19  17.1   3.83   17.3    17.1   3.11  10.4  24.4  14.0
cyl    2 19   7.0   1.54    8.0     7.1   0.00   4.0   8.0   4.0
disp   3 19 290.4 110.17  275.8   289.7 124.83 120.1 472.0 351.9
hp     4 19 160.3  53.91  175.0   161.1  77.10  62.0 245.0 183.0
drat   5 19   3.3   0.39    3.1     3.3   0.22   2.8   3.9   1.2
wt     6 19   3.8   0.78    3.5     3.8   0.45   2.5   5.4   3.0
qsec   7 19  18.2   1.75   17.8    18.1   1.19  15.4  22.9   7.5
vs*    8 19   1.4   0.50    1.0     1.4   0.00   1.0   2.0   1.0
am*    9 19   1.0   0.00    1.0     1.0   0.00   1.0   1.0   0.0
gear  10 19   3.2   0.42    3.0     3.2   0.00   3.0   4.0   1.0
carb  11 19   2.7   1.15    3.0     2.8   1.48   1.0   4.0   3.0
      skew kurtosis    se
mpg   0.01    -0.33  0.88
cyl  -0.95    -0.24  0.35
disp  0.05    -1.01 25.28
hp   -0.01    -0.93 12.37
drat  0.50    -1.06  0.09
wt    0.98     1.06  0.18
qsec  0.85     1.66  0.40
vs*   0.50    -1.86  0.11
am*    NaN      NaN  0.00
gear  1.31     0.42  0.10
carb -0.14    -1.47  0.26
------------------------------------------------ 
group: 1
     var  n  mean    sd median trimmed   mad  min   max range
mpg    1 12  24.5  6.42   23.7    24.5  7.93 15.0  33.9  18.9
cyl    2 13   5.1  1.55    4.0     4.9  0.00  4.0   8.0   4.0
disp   3 13 143.5 87.20  120.3   131.2 58.86 71.1 351.0 279.9
hp     4 13 126.8 84.06  109.0   114.7 63.75 52.0 335.0 283.0
drat   5 13   4.0  0.36    4.1     4.0  0.27  3.5   4.9   1.4
wt     6 13   2.4  0.62    2.3     2.4  0.68  1.5   3.6   2.1
qsec   7 13  17.4  1.79   17.0    17.4  2.34 14.5  19.9   5.4
vs*    8 13   1.5  0.52    2.0     1.6  0.00  1.0   2.0   1.0
am*    9 13   2.0  0.00    2.0     2.0  0.00  2.0   2.0   0.0
gear  10 13   4.4  0.51    4.0     4.4  0.00  4.0   5.0   1.0
carb  11 13   2.9  2.18    2.0     2.6  1.48  1.0   8.0   7.0
      skew kurtosis    se
mpg  -0.01    -1.35  1.85
cyl   0.87    -0.15  0.43
disp  1.33     2.17 24.19
hp    1.36     2.46 23.31
drat  0.79     1.83  0.10
wt    0.21    -0.65  0.17
qsec -0.23    -1.10  0.50
vs*  -0.14    -2.36  0.14
am*    NaN      NaN  0.00
gear  0.42    -2.06  0.14
carb  0.98     1.07  0.60
# Пакет doBy. Обладает мощным функционалом. Пример приведен ниже:
 
summaryBy(mpg + wt ~ cyl + vs, data = mtcars,
          FUN = function(x) { c(m = mean(x), s = sd(x)) } )
  cyl vs mpg.m mpg.s wt.m wt.s
1   4  0    26    NA  2.1   NA
2   4  1    NA    NA  2.3 0.60
3   6  0    21  0.75  2.8 0.13
4   6  1    19  1.63  3.4 0.12
5   8  0    15  2.56  4.0 0.76
Источник

Дисперсия и стандартное отклонение

Дисперсия — мера разброса значений наблюдений относительно среднего.

[sigma^2_X = frac{sum_{i = 1}^n(x_i – bar{x})^2}{n – 1},]

где

  • (x_1, …, x_n) — наблюдения;
  • (bar{x}) — среднее всех наблюдений;
  • (X) — вектор всех наблюдений;
  • (n) — количество наблюдений.

Представим, что у нас есть следующие данные:

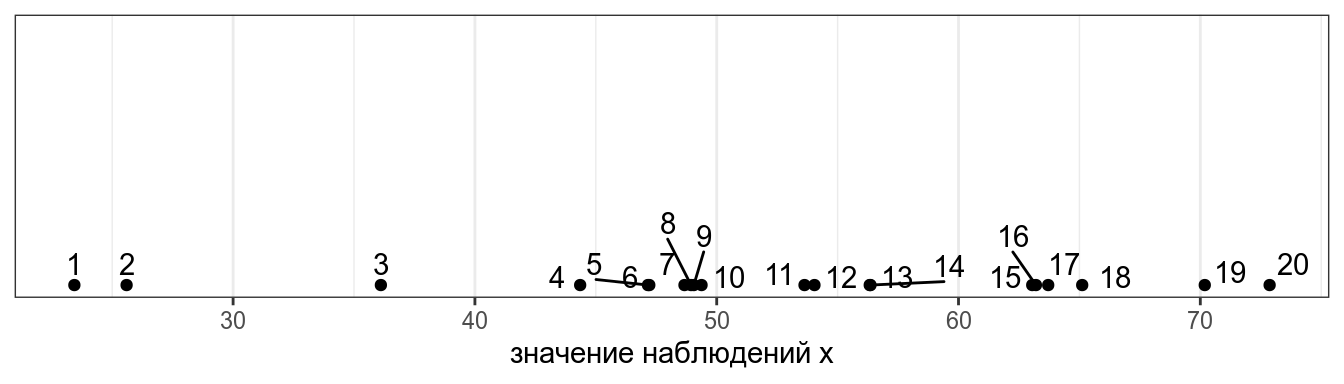
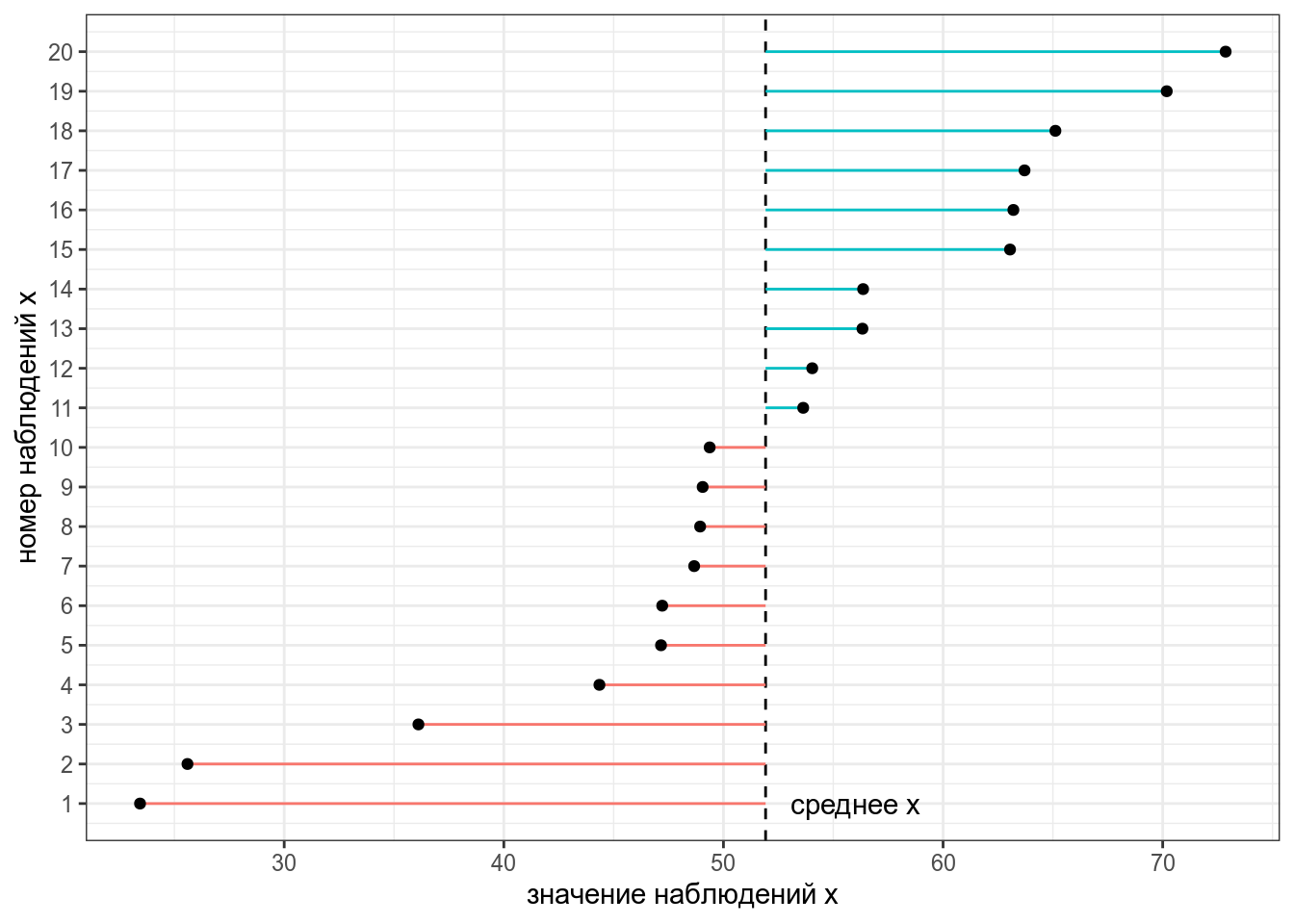
Тогда дисперсия — это сумма квадратов расстояний от каждой точки до среднего выборки (пунктирная линия) разделенное на количество наблюдений – 1 (по духу эта мера — обычное среднее, но если вас инетересует разница смещенной и несмещенной оценки дисперсии, см. видео).

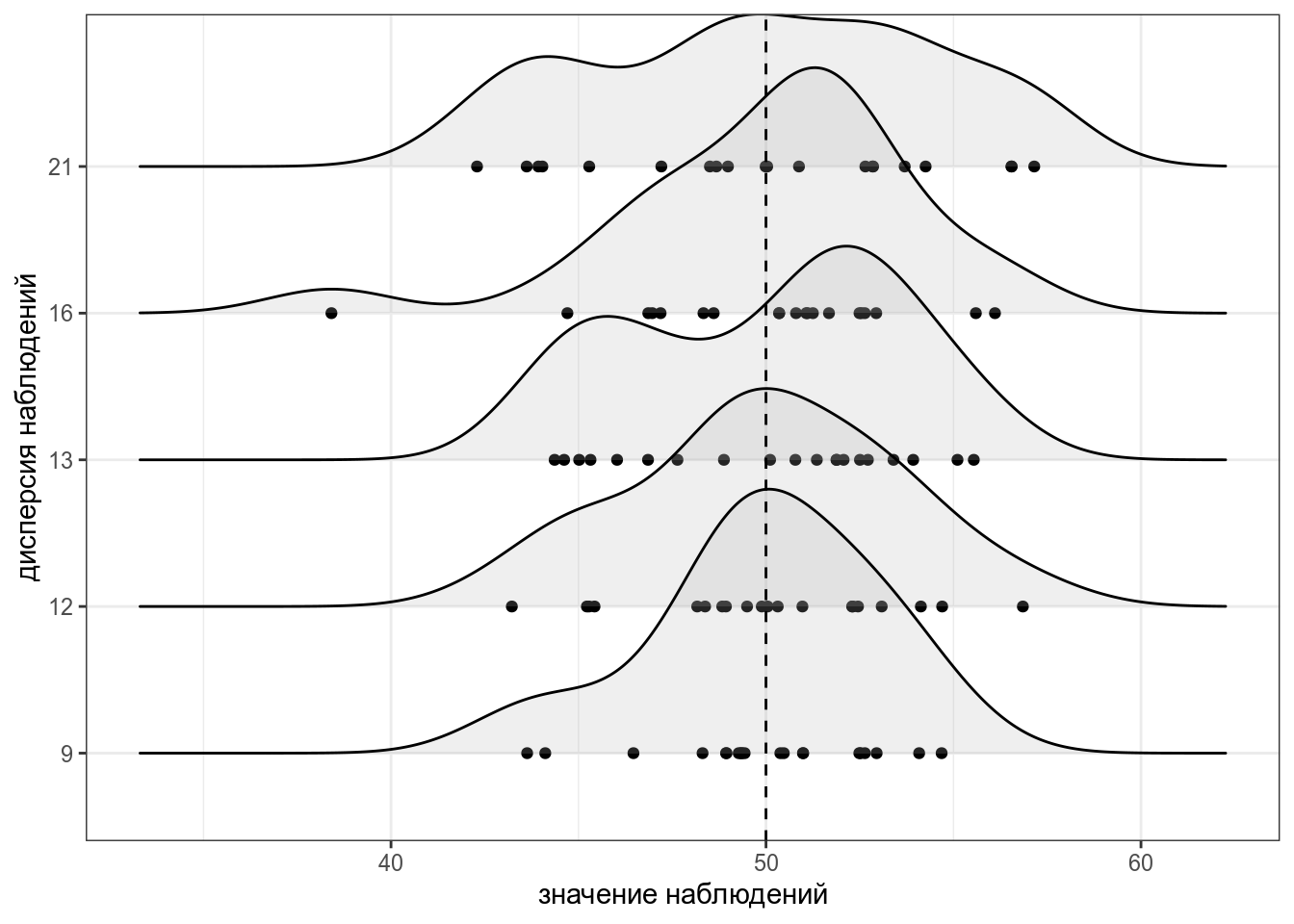
Для того чтобы было понятнее, что такое дисперсия, давайте рассмотрим несколько расспределений с одним и тем же средним, но разными дисперсиями:

В R дисперсию можно посчитать при помощи функции var()3.

set.seed(42)
x <- rnorm(20, mean = 50, sd = 10)
var(x)
[1] 172.2993

Проверим, что функция выдает то же, что мы записали в формуле.

var(x) == sum((x - mean(x))^2)/(length(x)-1)
[1] TRUE

Так как дисперсия является квадратом отклонения, то часто вместо нее используют более интерпретируемое стандартное отклонение (sigma) — корень из дисперсии. В R ее можно посчитать при помощи функции sd():

[1] 13.12628
[1] TRUE

Посчитайте дисперсию переменной sleep_total в датасете msleep, встроенный в tidyverse. Ответ округлите до двух знаков после запятой.

Посчитайте стандартное отклонение переменной sleep_total в датасете msleep, встроенный в tidyverse. Ответ округлите до двух знаков после запятой.

z-преобразование

z-преобразование (еще используют термин нормализация) — это способ представления данных в виде расстояний от среднего, измеряемых в стандартных отклонениях. Для того чтобы его получить, нужно из каждого наблюдения вычесть среднее и результат разделить на стандартное отклонение.

[x_i = frac{x_i – bar{x}}{sigma_X}]

Если все наблюдения z-преобразовать, то получиться распределение с средним в 0 и стандартным отклонением 1 (или очень близко к ним).

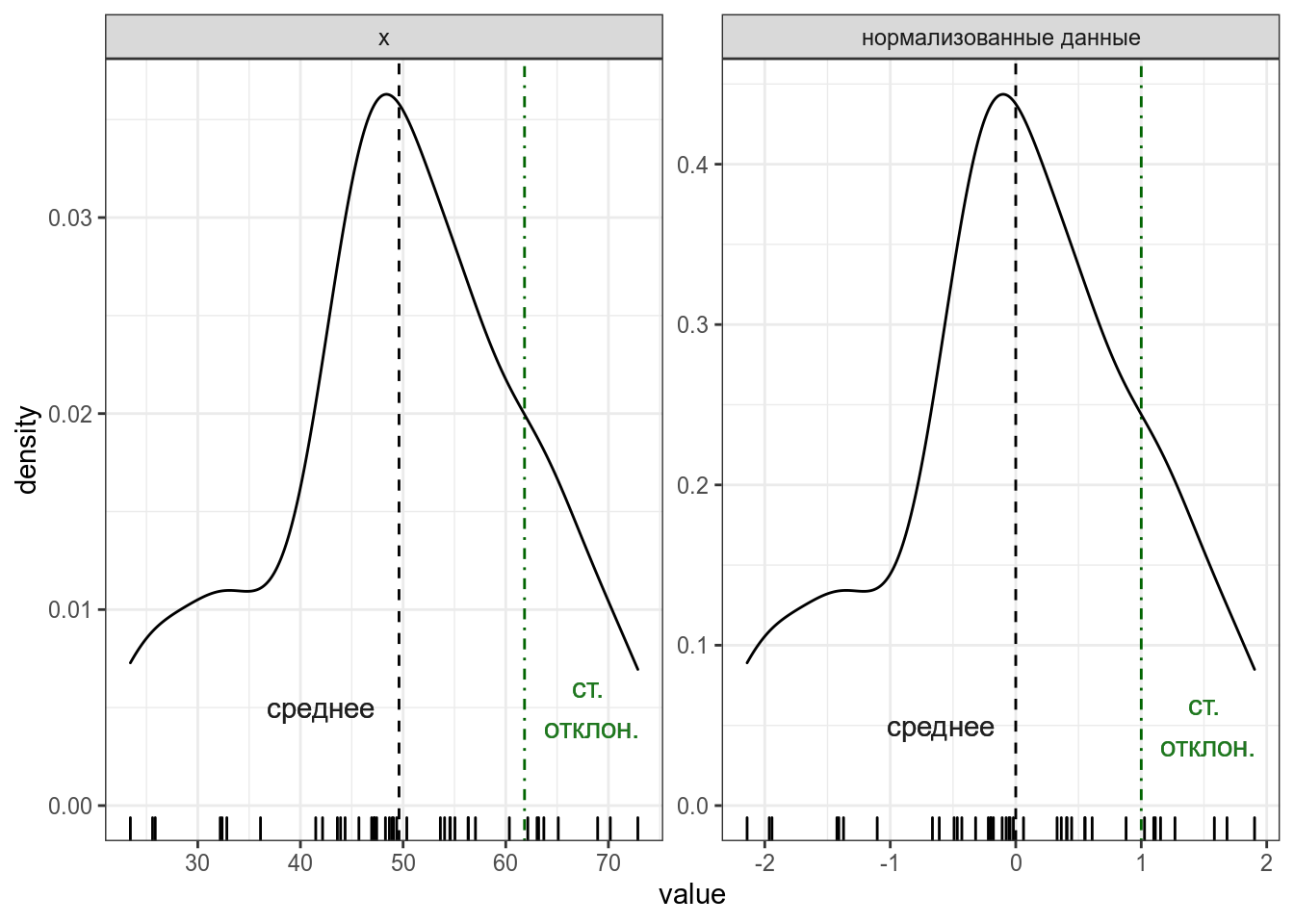
Само по себе (z)-преобразование ничего особенного нам про данные не говорит. Однако это преобразование позволяет привести к “общему знаменателю” разные переменные. Т. е. это преобразование ничего нам не говорит про конкретный набор данных, но позволяет сравнивать разные наборы данных.

В R z-преобразование можно сделать при помощи функции scale(). Эта функция вовзращает матрицу, поэтому я использую индекс [,1], чтобы результат был вектором.

set.seed(42)
x <- rnorm(20, mean = 50, sd = 10)
scale(x)[,1]
 [1]  0.8982271 -0.5764146  0.1304317  0.3359234  0.1617734 -0.2270593
 [7]  1.0053127 -0.2183246  1.3914857 -0.1939880  0.8478787  1.5958251
[13] -1.2042865 -0.3586002 -0.2477787  0.3382758 -0.3627629 -2.1699785
[19] -2.0054319  0.8594918

Проверим, что функция выдает то же, что мы записали в формуле.

scale(x)[,1] == (x-mean(x))/sd(x)
 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[16] TRUE TRUE TRUE TRUE TRUE

Однаждый я заполучил градусник со шкалой Фаренгейта и целый год измерял температуру в Москве при помощи градусников с шкалой Фарингейта и Цельсия. В датасет записаны средние значения для каждого месяца. Постройте график нормализованных и ненормализованных измерений. Что можно сказать про измерения, сделанные разными термометрами?

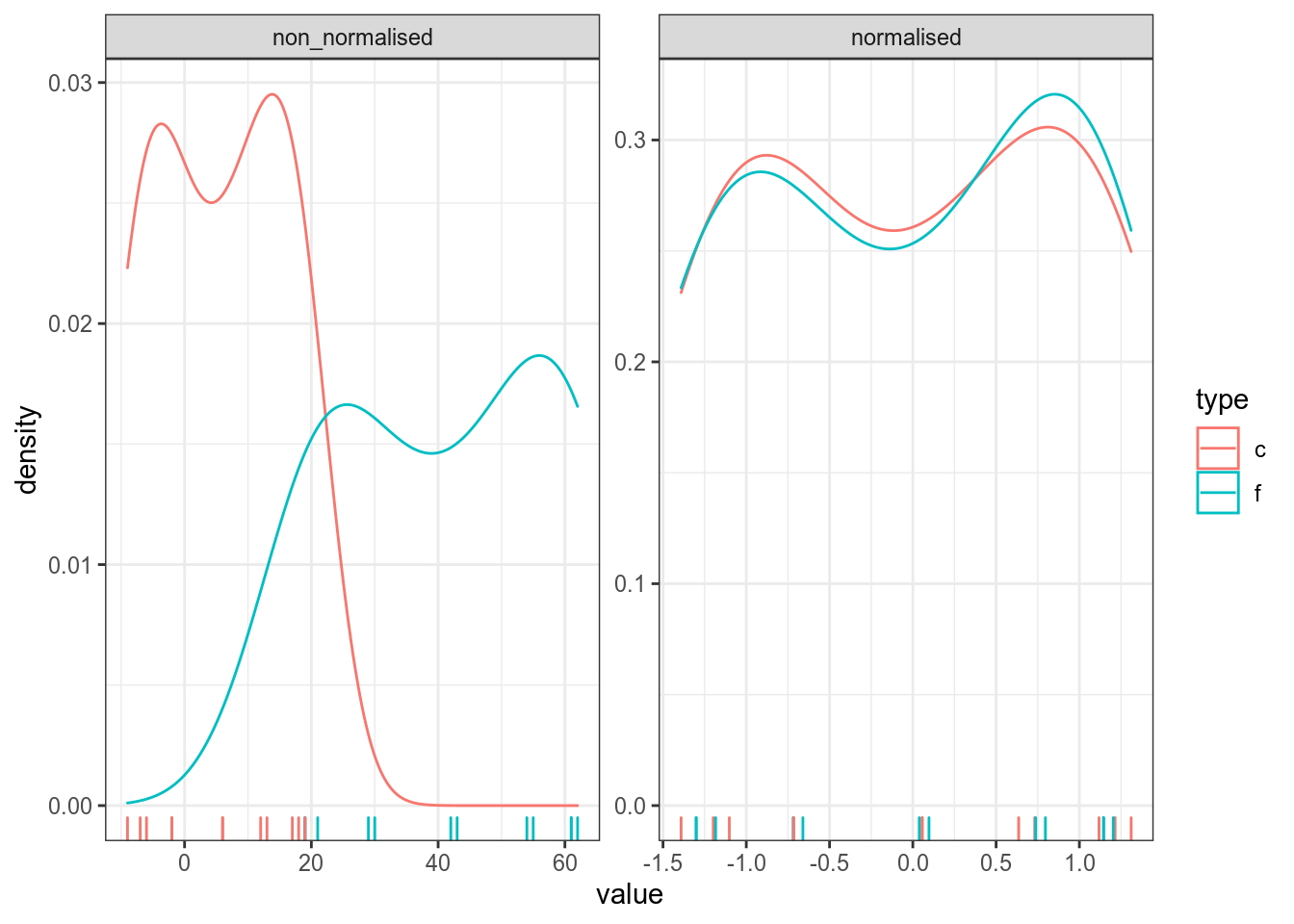
Ковариация

Ковариация — эта мера ассоциации двух переменных.

[cov(X, Y) = frac{sum_{i = 1}^n(x_i – bar{x})(y_i-bar{y})}{n – 1},]

где

  • ((x_1, y_1), …, (x_n, y_n)) — пары наблюдений;
  • (bar{x}, bar{y}) — средние наблюдений;
  • (X, Y) — векторы всех наблюдений;
  • (n) — количество наблюдений.

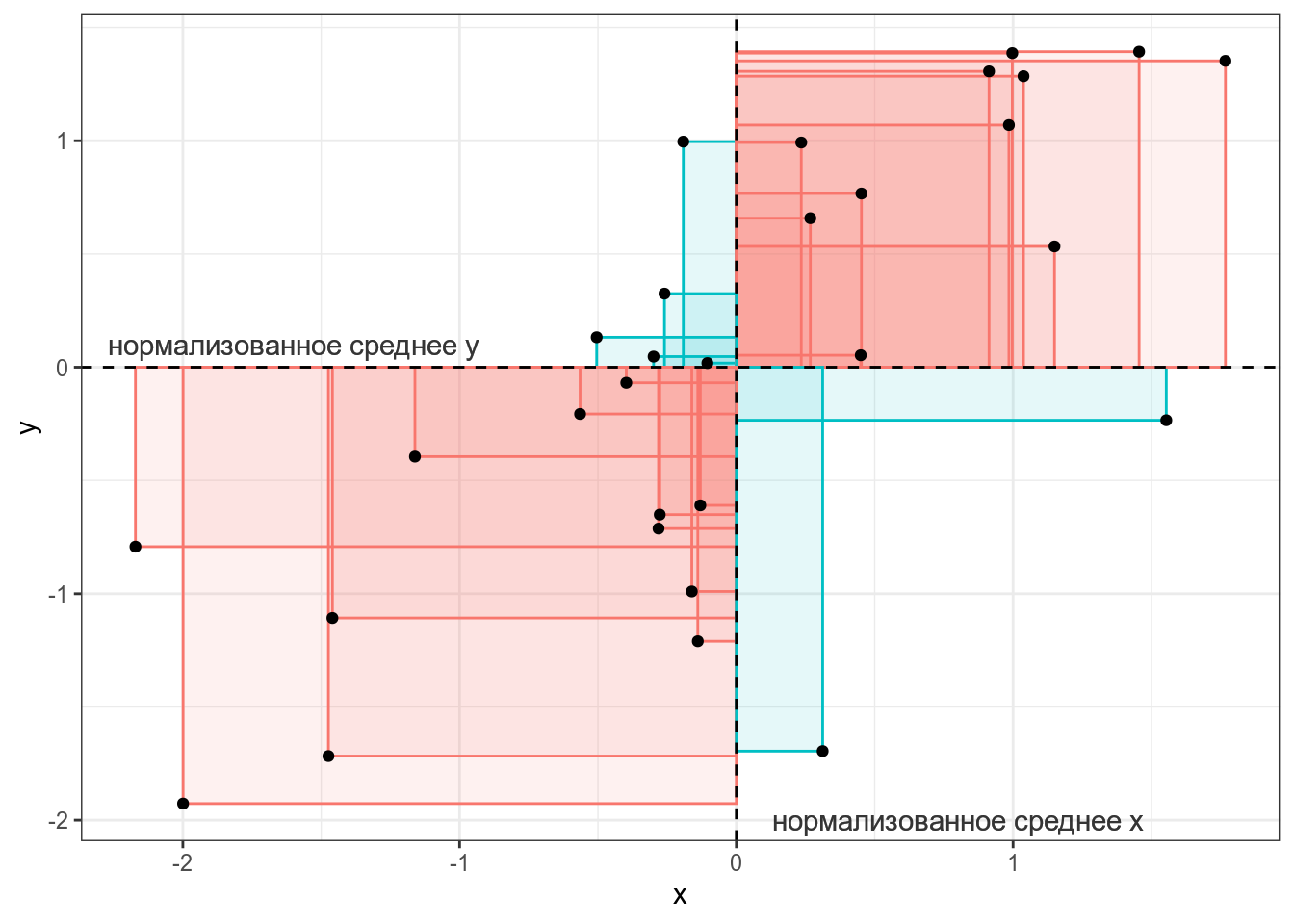
Представим, что у нас есть следующие данные:

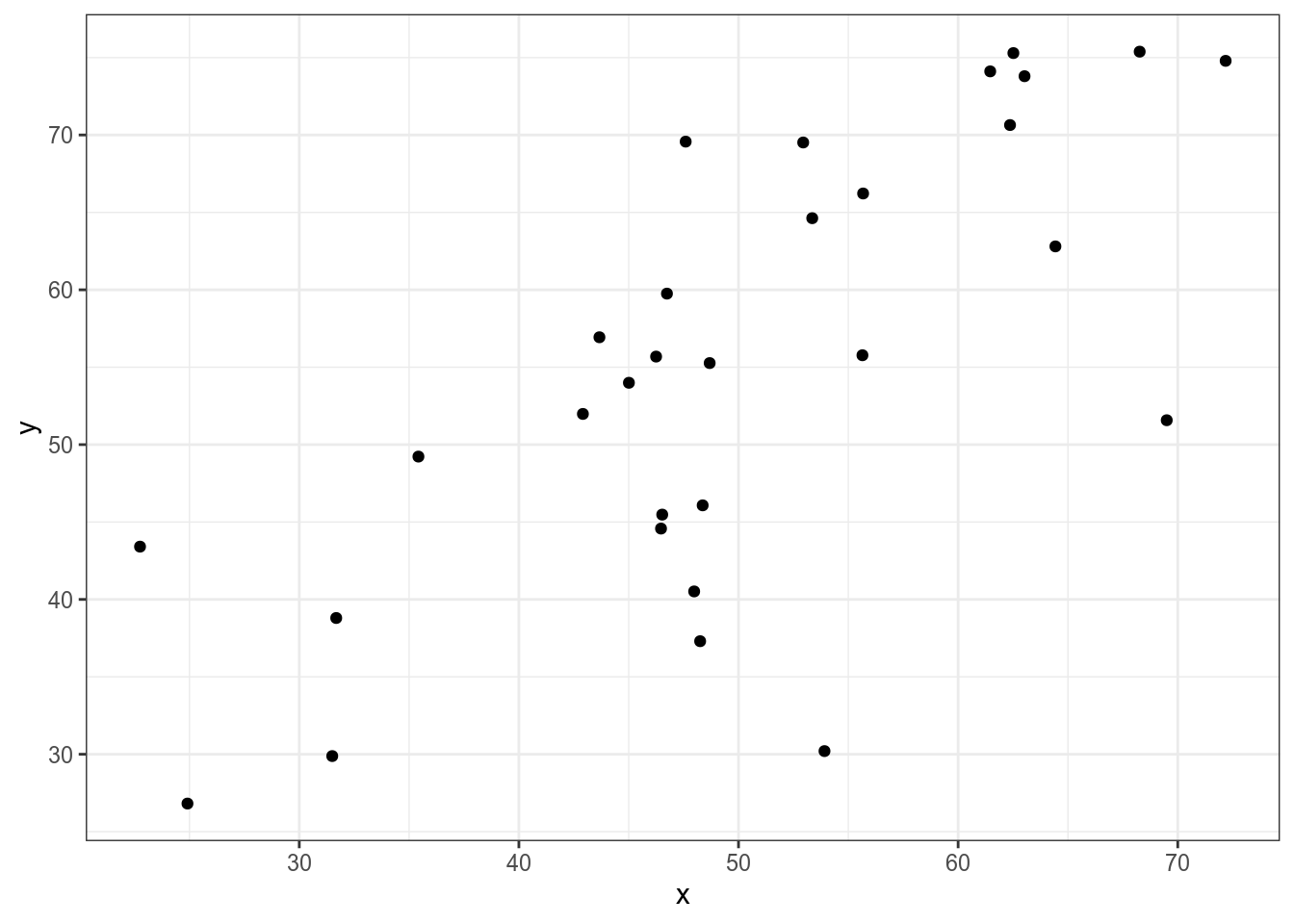
Тогда, согласно формуле, для каждой точки вычисляется следующая площадь (пуктирными линиями обозначены средние):

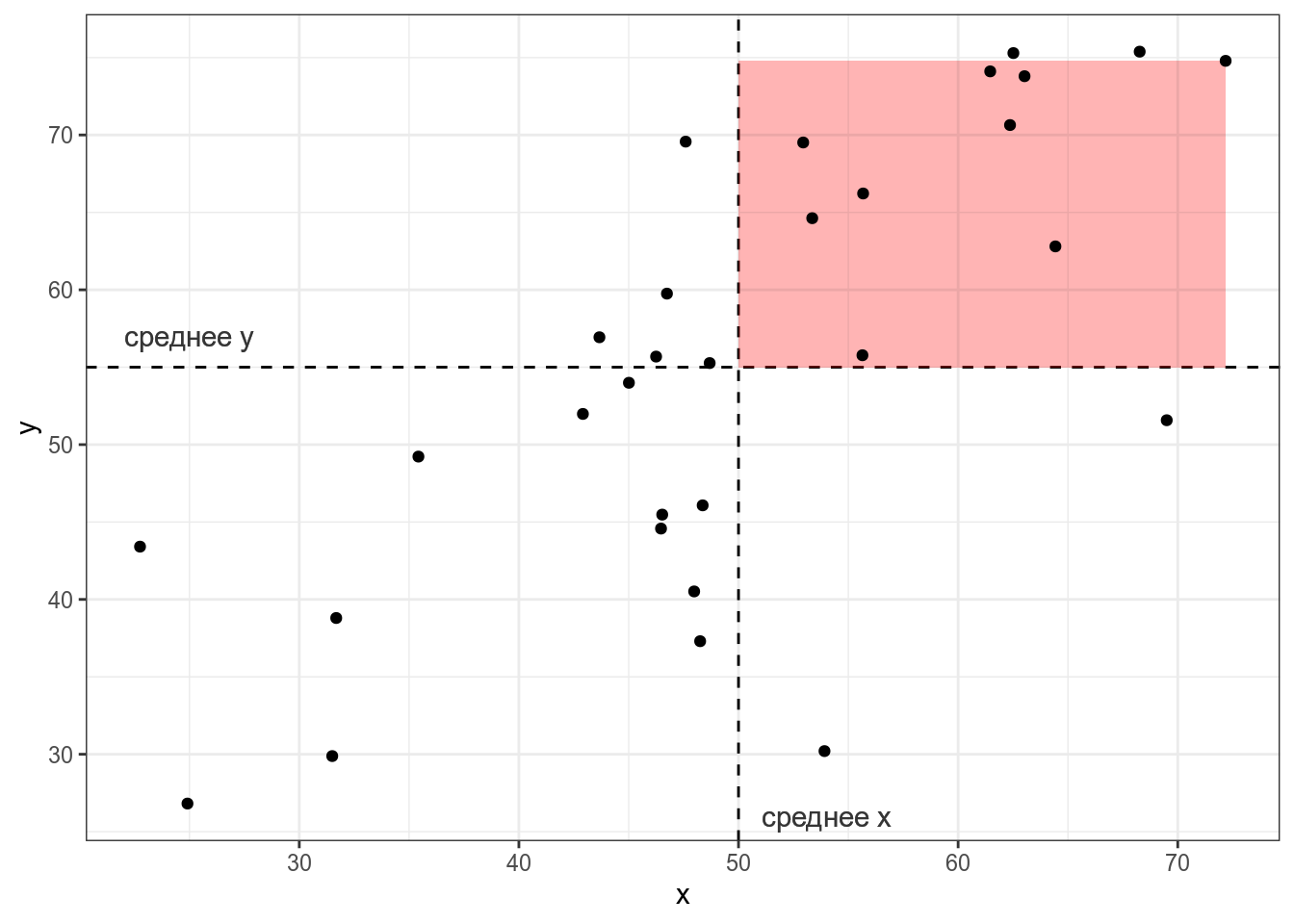
Если значения (x_i) и (y_i) какой-то точки либо оба больше, либо оба меньше средних (bar{x}) и (bar{y}), то получившееся произведение будет иметь знак +, если же наоборот — знак -. На графике это показано цветом.

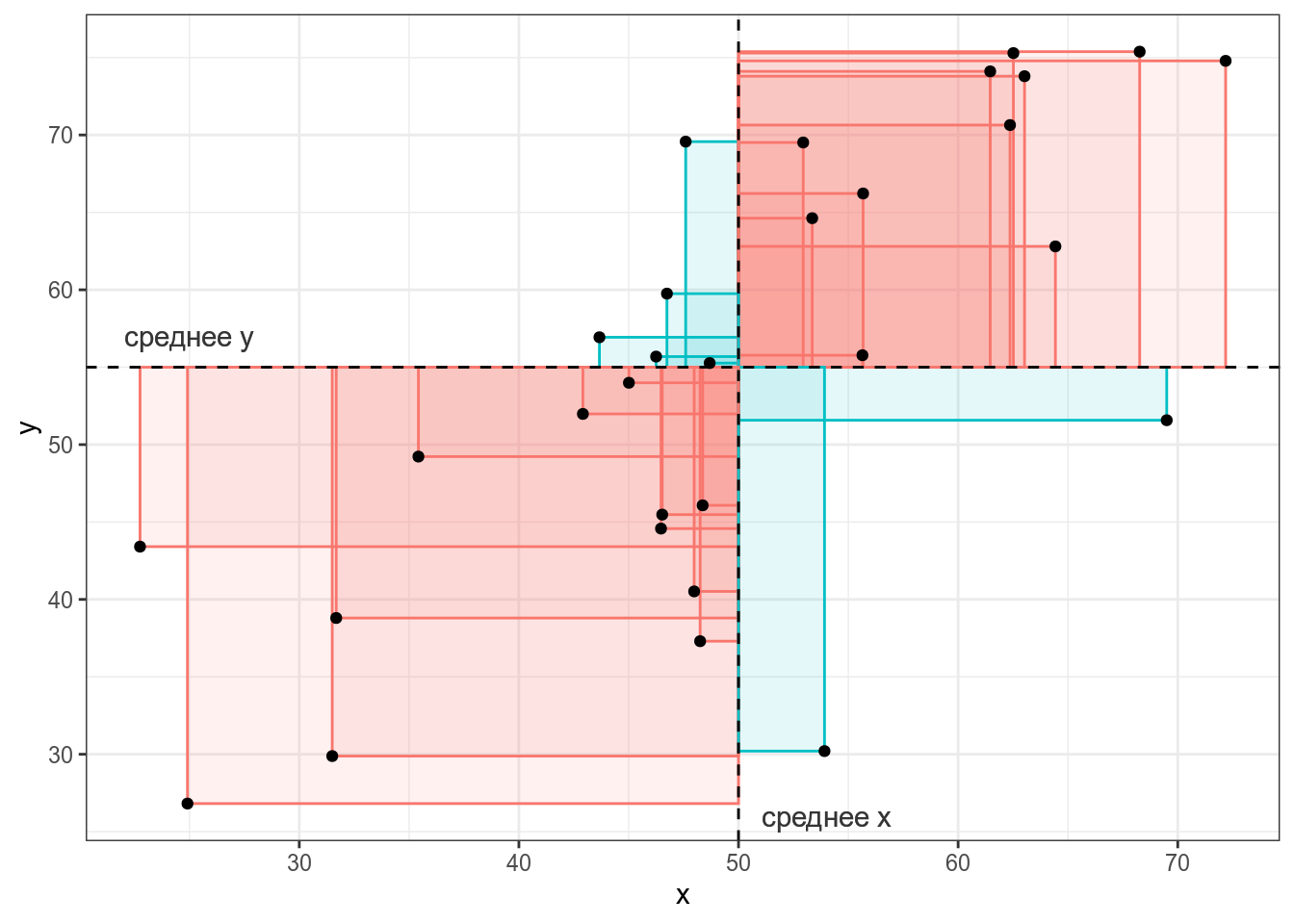
Таким образом, если много красных прямоугольников, то значение суммы будет положительное и обозначать положительную связь (чем больше (x), тем больше (y)), а если будет много синий прямоугольников, то значение суммы отрицательное и обозначать положительную связь (чем больше (x), тем меньше (y)). Непосредственно значение ковариации не очень информативно, так как может достаточно сильно варьироваться от датасета к датасету.

В R ковариацию можно посчитать при помощи функции cov().

set.seed(42)
x <- rnorm(10, mean = 50, sd = 10)
y <-  x + rnorm(10, sd = 10)
cov(x, y)
[1] 18.72204
[1] -37.44407

Как видно, простое умножение на два удвоило значение ковариации, что показывает, что непосредственно ковариацию использовать для сравнения разных датасетов не стоит.

Проверим, что функция выдает то же, что мы записали в формуле.

cov(x, y) == sum((x-mean(x))*(y - mean(y)))/(length(x)-1)
[1] TRUE

Корреляция

Корреляция — это мера ассоциации/связи двух числовых переменных. Помните, что бытовое применение этого термина к категориальным переменным (например, корреляция цвета глаз и успеваемость на занятиях по R) не имеет смысла с точки зрения статистики.

Корреляция Пирсона

Коэффициент корреляции Пирсона — базовый коэффициент ассоциации переменных, однако стоит помнить, что он дает неправильную оценку, если связь между переменными нелинейна.

[rho_{X,Y} = frac{cov(X, Y)}{sigma_Xtimessigma_Y} = frac{1}{n-1}timessum_{i = 1}^nleft(frac{x_i-bar{x}}{sigma_X}timesfrac{y_i-bar{y}}{sigma_Y}right),]

где

  • ((x_1, y_1), …, (x_n, y_n)) — пары наблюдений;
  • (bar{x}, bar{y}) — средние наблюдений;
  • (X, Y) — векторы всех наблюдений;
  • (n) — количество наблюдений.

Последнее уравнение показывает, что коэффициент корреляции Пирсона можно представить как среднее (с поправкой, поэтому (n-1), а не (n)) произведение (z)-нормализованных значений двух переменных.

Эта нормализация приводит к тому, что

  • значения корреляции имеют те же свойства знака коэффициента что и ковариация:
    • если коэффициент положительный (т. е. много красных прямоугольников) — связь между переменными положительная (чем больше (x), тем больше (y)),
    • если коэффициент отрицательный (т. е. много синих прямоугольников) — связь между переменными отрицательная (чем больше (x), тем меньше (y));
  • значение корреляции имееет независимое от типа данных интеретация:
    • если модуль коэффициента близок к 1 или ему равен — связь между переменными сильная,
    • если модуль коэффициента близок к 0 или ему равен — связь между переменными слабая.

Для того чтобы было понятнее, что такое корреляция, давайте рассмотрим несколько расспределений с разными значениями корреляции:

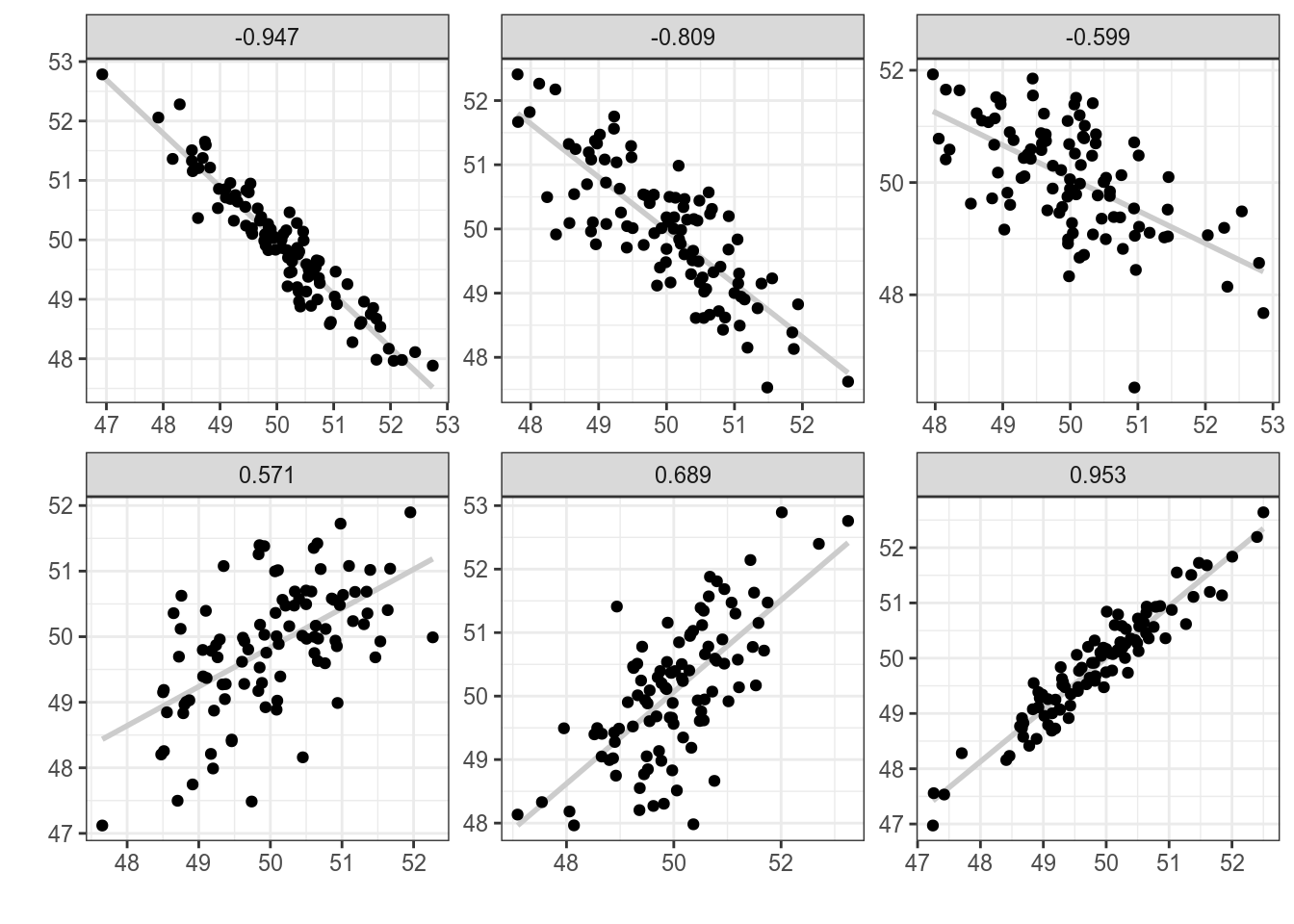
Как видно из этого графика, чем ближе модуль корреляции к 1, тем боллее компактно расположены точки друг к другу, чем ближе к 0, тем более рассеяны значения. Достаточно легко научиться приблизительно оценивать коэфициент корреляции на глаз, поиграв 2–5 минут в игру “Угадай корреляцию” здесь или здесь.

В R коэффициент корреляции Пирсона можно посчитать при помощи функции cor().

set.seed(42)
x <- rnorm(15, mean = 50, sd = 10)
y <-  x + rnorm(15, sd = 10)
cor(x, y)
[1] 0.6659041

Проверим, что функция выдает то же, что мы записали в формуле.

cor(x, y) == cov(x, y)/(sd(x)*sd(y))
[1] TRUE
cor(x, y) == sum(scale(x)*scale(y))/(length(x)-1)
[1] TRUE

Посчитайте на основе датасета с температурой корреляцию между разными измерениями в шкалах Фарингейта и Цельсия? Результаты округлите до трех знаков после запятой.

Ранговые корреляции Спирмана и Кендалла

Коэффициент корреляции Пирсона к сожалению, чувствителен к значениям наблюдений. Если связь между переменными нелинейна, то оценка будет получаться смещенной. Рассмотрим, например, словарь [Ляшевской, Шарова 2011]:

freqdict <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/freq_dict_2011.csv")
freqdict %>% 
  arrange(desc(freq_ipm)) %>% 
  mutate(id = 1:n()) %>% 
  slice(1:100) ->
  filered_freqdict

filered_freqdict %>% 
  ggplot(aes(id, freq_ipm, label = lemma))+
  geom_point()+
  ggrepel::geom_text_repel()+
  scale_y_log10()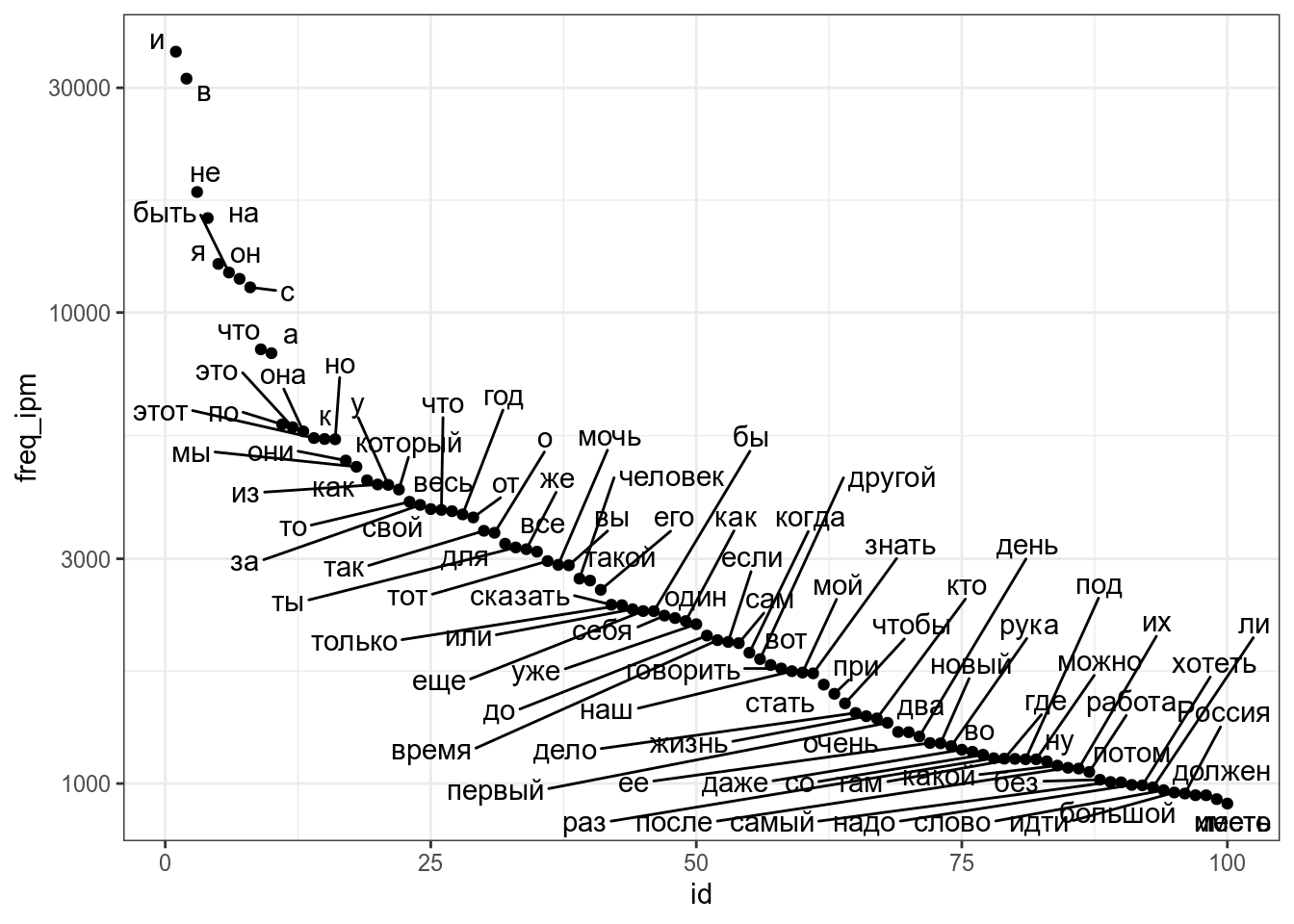

В целом корреляция между рангом и частотой должна быть высокая, однако связь между этими переменными нелинейна, так что коэффициент корреляции Пирсона не такой уж и высокий:

cor(filered_freqdict$freq_ipm, filered_freqdict$id)
[1] -0.6307876

Для решения той проблемы обычно используют ранговые коэффециенты коррляции Спирмана и Кендала, которые принимают во внимание ранг значения, а не его непосредственное значение.

cor(filered_freqdict$freq_ipm, filered_freqdict$id, method = "spearman")
[1] -1
cor(filered_freqdict$freq_ipm, filered_freqdict$id, method = "kendall")
[1] -1

Давайте сравним с предыдущими наблюдениями и их логаотфмамиы:

cor(x, y) == cor(log(x), log(y))
[1] FALSE
cor(x, y, method = "spearman") == cor(log(x), log(y), method = "spearman")
[1] TRUE
cor(x, y, method = "kendall") == cor(log(x), log(y), method = "kendall")
[1] TRUE

Регрессионный анализ

Основы

Суть регрессионного анализа в моделировании связи между двумя и более переменными при помощи прямой на плоскости. Формула прямой зависит от двух параметров: свободного члена (intercept) и углового коэффициента (slope).

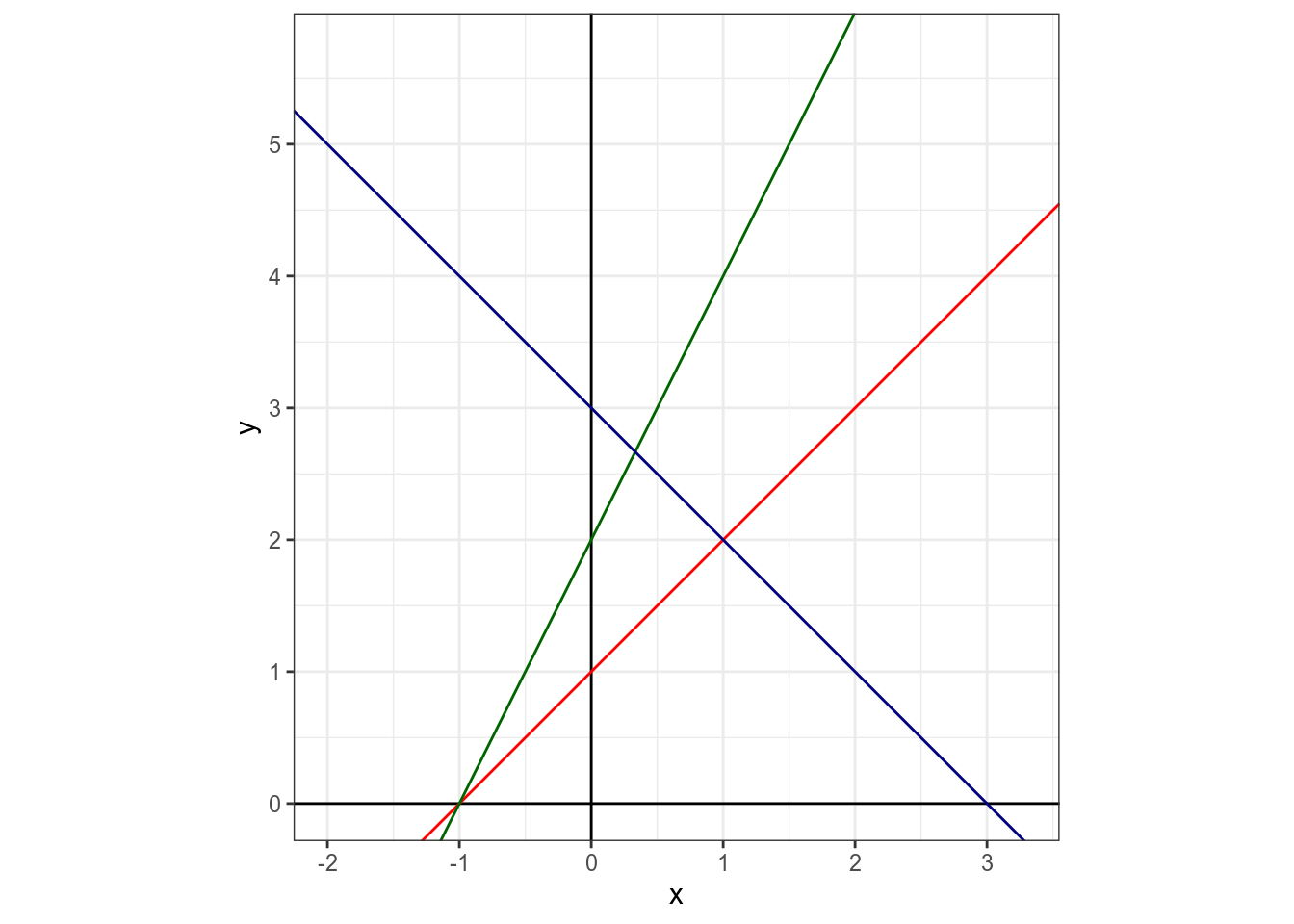
Укажите значение свободного члена для красной прямой.

Укажите значение свободного члена для зеленой прямой.

Укажите значение свободного члена для синей прямой.

Укажите значение углового коэффициента для красной прямой.

Укажите значение углового коэффициента для зеленой прямой.

Укажите значение углового коэффициента для синей прямой.

Когда мы пытаемся научиться предсказывать данные одной переменной (Y) при помощи другой переменной (X), мы получаем похожую формулу:

[y_i = hatbeta_0 + hatbeta_1 times x_i + epsilon_i,]
где

  • (x_i) — (i)-ый элемент вектора значений (X);
  • (y_i) — (i)-ый элемент вектора значений (Y);
  • (hatbeta_0) — оценка случайного члена (intercept);
  • (hatbeta_1) — оценка углового коэффициента (slope);
  • (epsilon_i) — (i)-ый остаток, разница между оценкой модели ((hatbeta_0 + hatbeta_1 times x_i)) и реальным значением (y_i); весь вектор остатков иногда называют случайным шумом (на графике выделены красным).

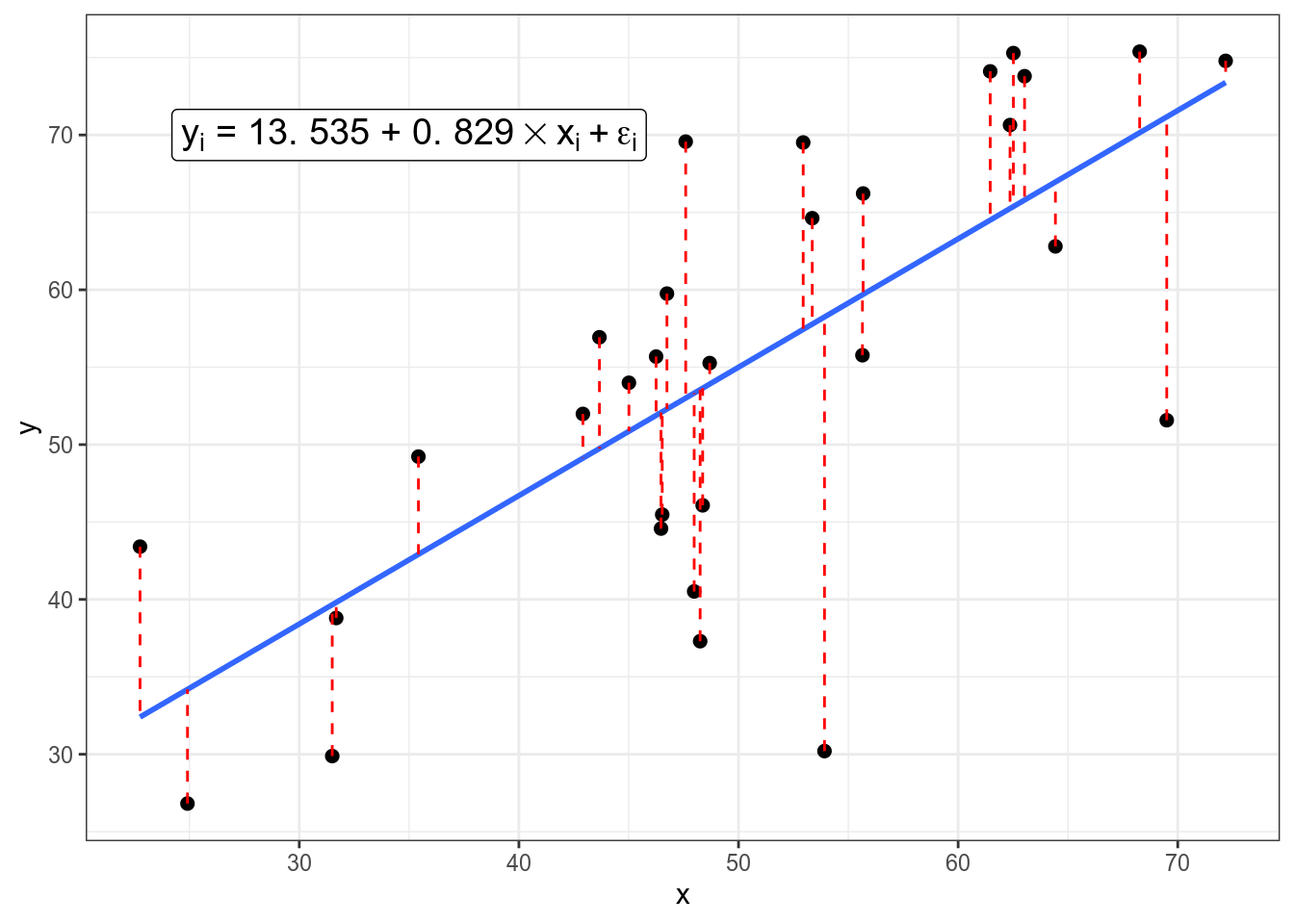
Задача регрессии — оценить параметры (hatbeta_0) и (hatbeta_1), если нам известны все значения (x_i) и (y_i) и мы пытаемся минимизировать значния (epsilon_i). В данном конкретном случае, задачу можно решить аналитически и получить следующие формулы:

[hatbeta_1 = frac{(sum_{i=1}^n x_itimes y_i)-ntimesbar x times bar y}{sum_{i = 1}^n(x_i-bar x)^2}]

[hatbeta_0 = bar y – hatbeta_1timesbar x]

Первая регрессия

Давайте попробуем смоделировать количество слов и в рассказах М. Зощенко в зависимости от длины рассказа:

zo <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_zoshenko.csv")

zo %>% 
  filter(word == "и") %>% 
  distinct() %>% 
  ggplot(aes(n_words, n))+
  geom_point()+
  labs(x = "количество слов в рассказе",
       y = "количество и")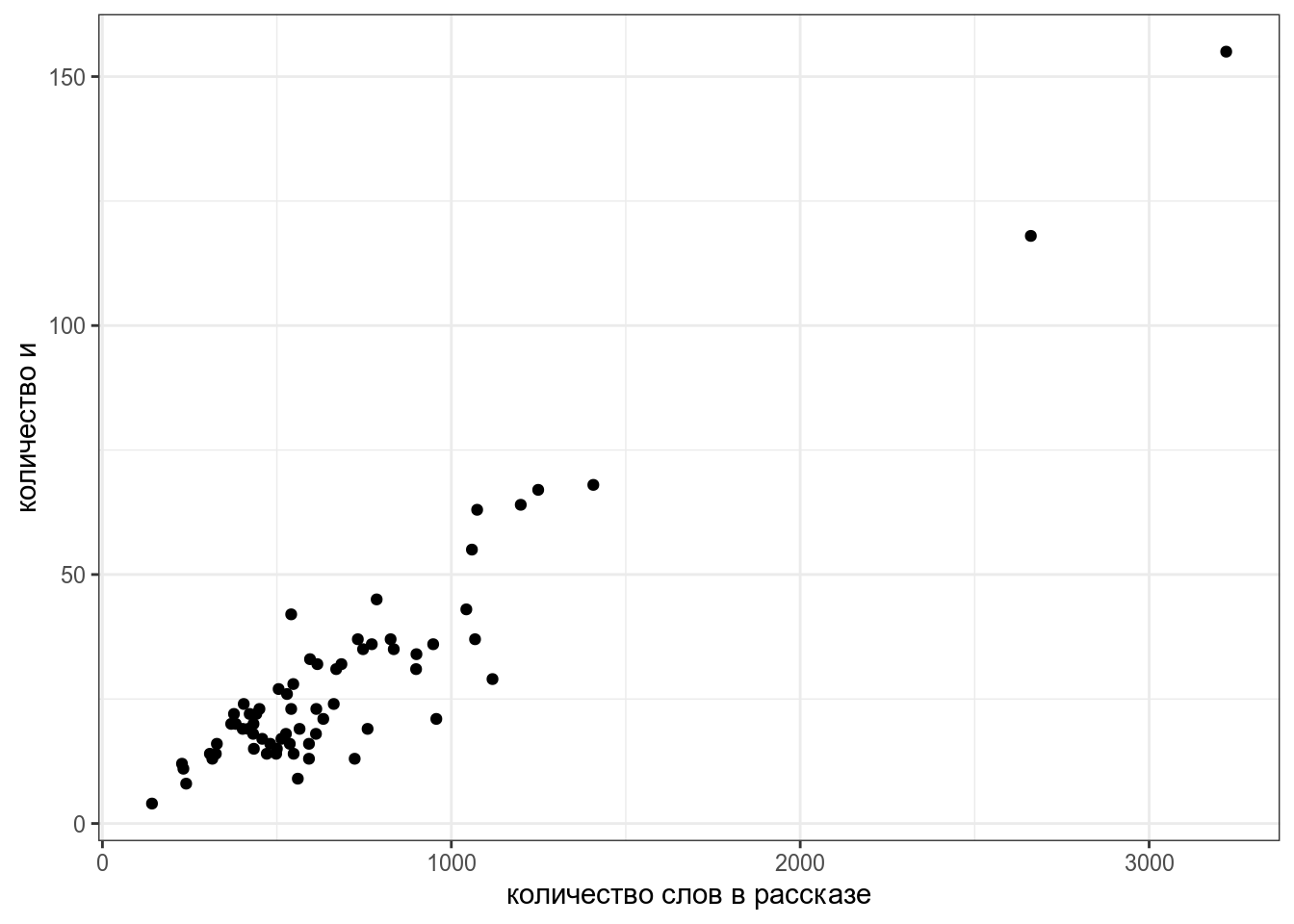

Мы видим, несколько одиночных точек, давайте избавимся от них и добавим регрессионную линию при помощи функции geom_smooth():

zo %>% 
  filter(word == "и",
         n_words < 1500) %>% 
  distinct() ->
  zo_filtered

zo_filtered %>%   
  ggplot(aes(n_words, n))+
  geom_point()+
  geom_smooth(method = "lm", se = FALSE)+
  labs(x = "количество слов в рассказе",
       y = "количество и")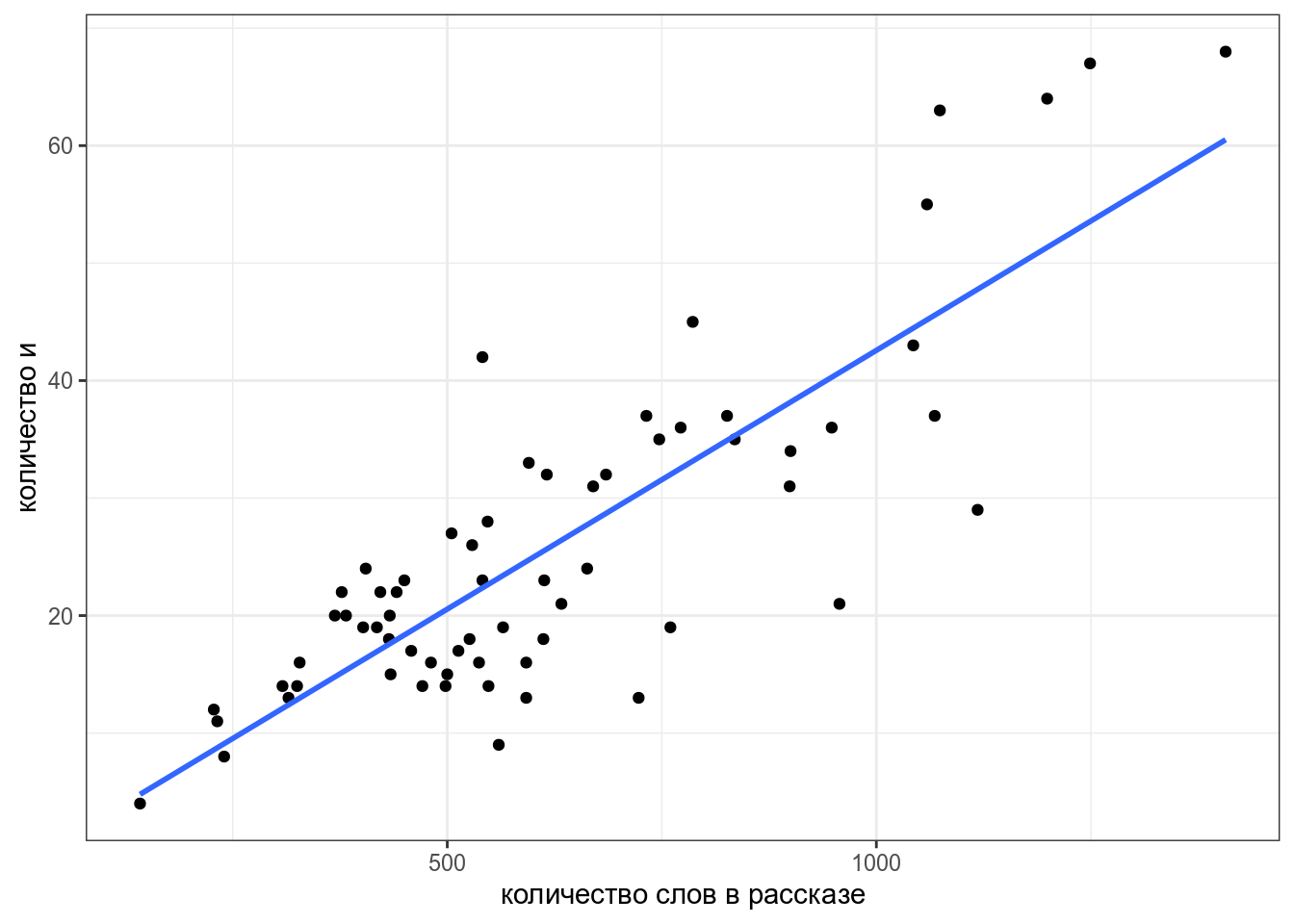

Чтобы получить формулу этой линии нужно запустить функцию, которая оценивает линейную регрессию:

fit <- lm(n~n_words, data = zo_filtered)
fit

Call:
lm(formula = n ~ n_words, data = zo_filtered)

Coefficients:
(Intercept)      n_words  
   -1.47184      0.04405

Вот мы и получили коэффициенты, теперь мы видим, что наша модель считает следующее:

[n = -1.47184 + 0.04405 times n_words]

Более подробную информцию можно посмотреть, если запустить модель в функцию summary():


Call:
lm(formula = n ~ n_words, data = zo_filtered)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.6830  -4.3835   0.8986   4.6486  19.6413 

Coefficients:
             Estimate Std. Error t value            Pr(>|t|)    
(Intercept) -1.471840   2.467149  -0.597               0.553    
n_words      0.044049   0.003666  12.015 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.945 on 64 degrees of freedom
Multiple R-squared:  0.6928,	Adjusted R-squared:  0.688 
F-statistic: 144.4 on 1 and 64 DF,  p-value: < 0.00000000000000022

В разделе Coefficients содержится информацию про наши коэффициенты:

  • Estimate – полученная оценка коэффициентов;
  • Std. Error – стандартная ошибка среднего;
  • t value – (t)-статистика, полученная при проведении одновыборочного (t)-теста, сравнивающего данный коэфициент с 0;
  • Pr(>|t|) – полученное (p)-значение;
  • Multiple R-squared и Adjusted R-squared — одна из оценок модели, показывает связь между переменными. Без поправок совпадает с квадратом коэффициента корреляции Пирсона:
cor(zo_filtered$n_words, zo_filtered$n)^2
[1] 0.6928376
  • F-statistic — (F)-статистика полученная при проведении теста, проверяющего, не являются ли хотя бы один из коэффицинтов статистически значимо отличается от нуля. Совпадает с результатами дисперсионного анализа (ANOVA).

Теперь мы можем даже предсказывать значения, которые мы еще не видели. Например, сколько будет и в рассказе Зощенко длиной 1000 слов?

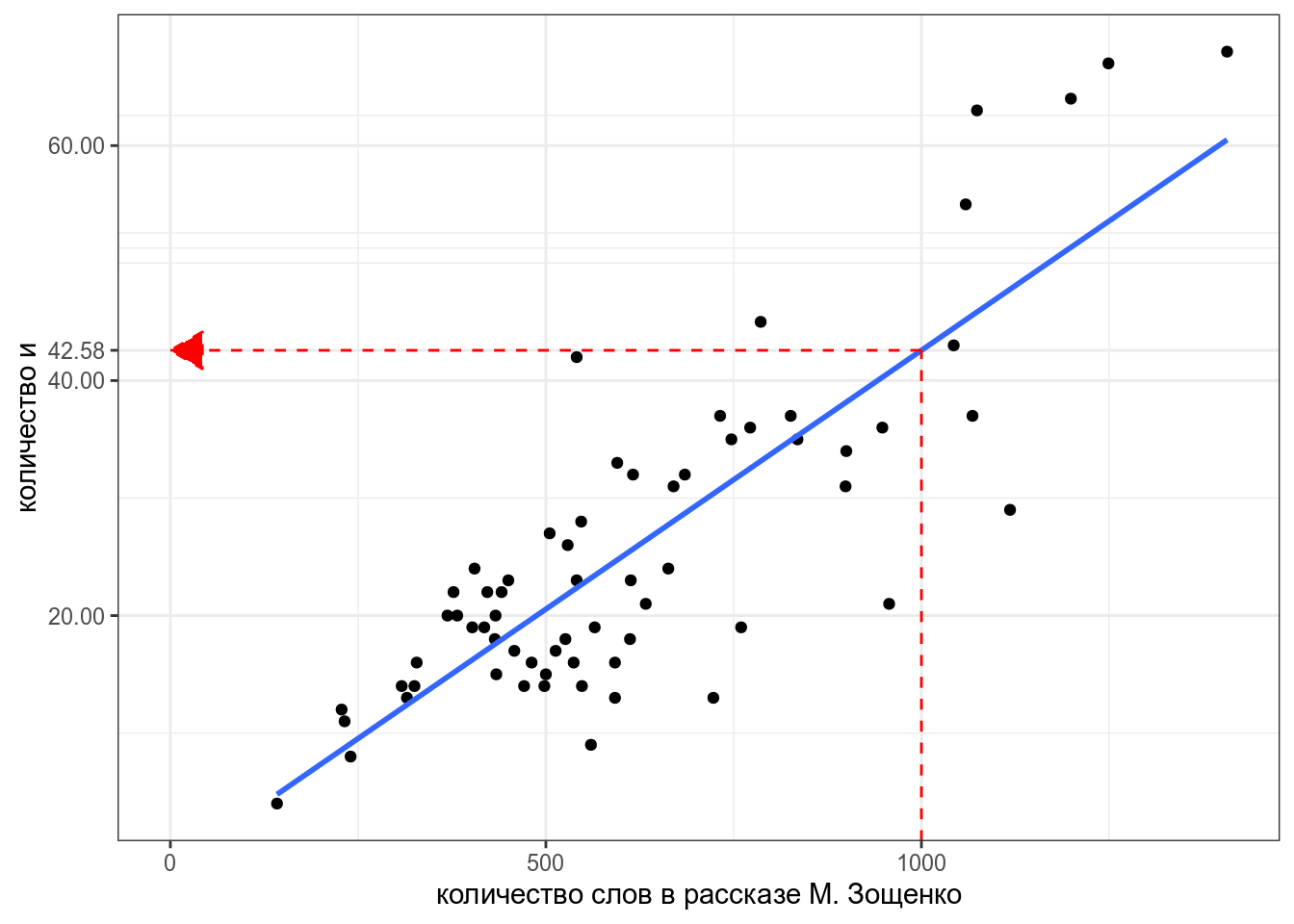
predict(fit, tibble(n_words = 1000))
       1 
42.57715

Постройте ленейную ргерессию на основании рассказов А. Чехова, предсказывая количество и на основании количства слов. При моделировании используйте только рассказы длиной меньше 2500 слов. Укажите свободный член получившейся модели, округлив его до 3 знаков после запятой.

Укажите угловой коффициент получившейся модели, округлив его до 3 знаков после запятой.

Укажите предсказания модели для рассказа длиной 1000 слов, округлив получнное значение до 3 знаков после запятой.

Категориальные переменные

Что если мы хотим включить в наш анализ категориальные переменные? Давайте рассмотрим простой пример с рассказами Чехова и Зощенко, которые мы рассматривали в прошлом разделе. Мы будем анализировать логарифм доли слов деньги:

chekhov <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_chekhov.tsv")
zoshenko <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_zoshenko.csv")

chekhov$author <- "Чехов"
zoshenko$author <- "Зощенко"

chekhov %>% 
  bind_rows(zoshenko) %>% 
  filter(str_detect(word, "деньг")) %>% 
  group_by(author, titles, n_words) %>% 
  summarise(n = sum(n)) %>% 
  mutate(log_ratio = log(n/n_words)) ->
  checkov_zoshenko

Визуализация выглядит так:

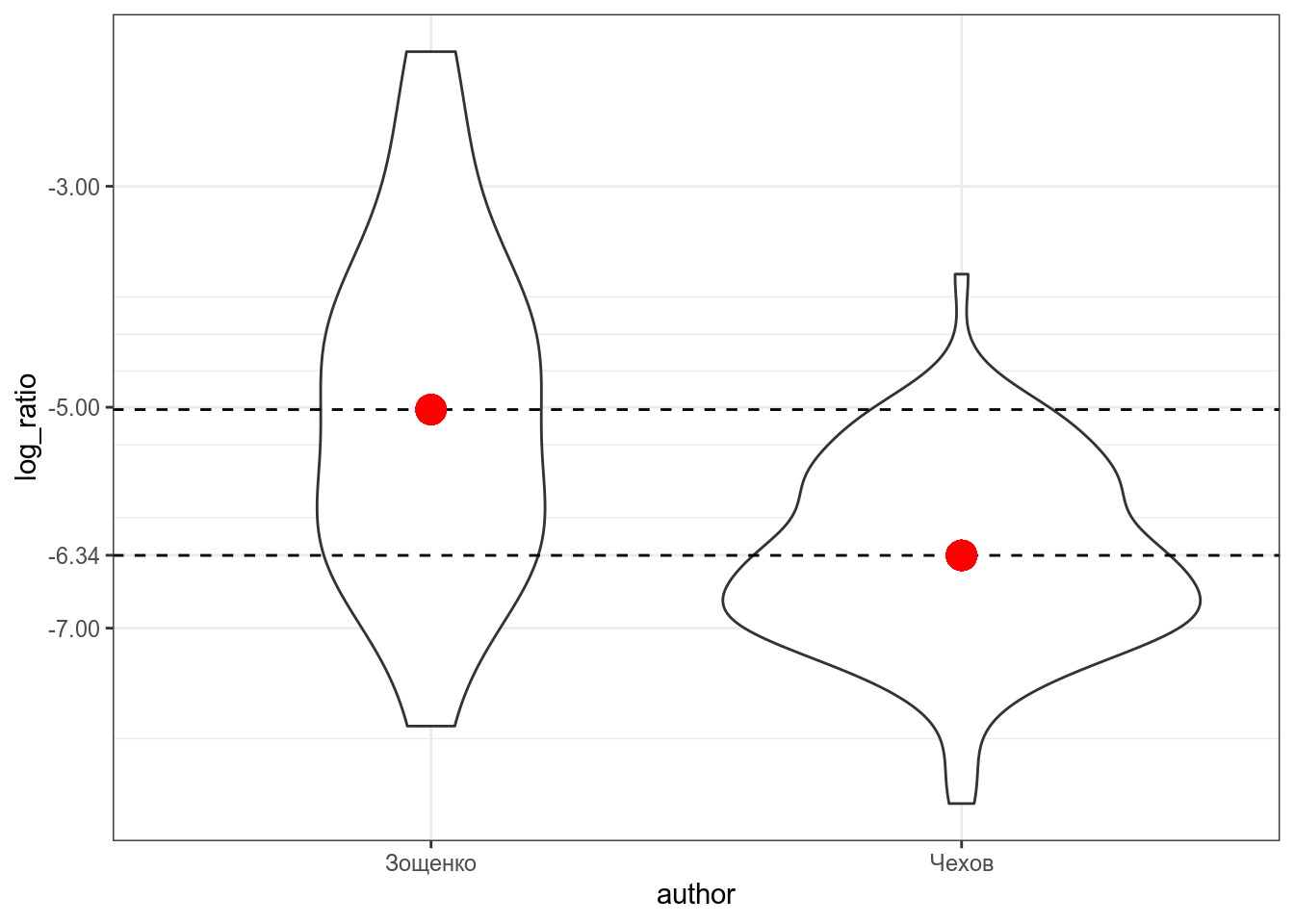
Красной точкой обозначены средние значения, так что мы видим, что между двумя писателями есть разница, но является ли она статистически значимой? В прошлом разделе, мы рассмотрели, что в таком случае можно сделать t-test:

t.test(log_ratio~author, 
       data = checkov_zoshenko, 
       var.equal =TRUE) # здесь я мухлюю, отключая поправку Уэлча

	Two Sample t-test

data:  log_ratio by author
t = 5.6871, df = 125, p-value = 0.00000008665
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.8606107 1.7793181
sample estimates:
mean in group Зощенко   mean in group Чехов 
            -5.021262             -6.341226

Разница между группами является статистически значимой (t(125) = 5.6871, p-value = 8.665e-08).

Для того, чтобы запустить регрессию на категориальных данных категориальная переменная автоматически разбивается на группу бинарных dummy-переменных:

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0),
       dummy_zoshenko = c(0, 1))

Дальше для регрессионного анализа выкидывают одну из переменных, так как иначе модель не сойдется (dummy-переменных всегда n-1, где n — количество категорий в переменной).

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0))

Если переменная dummy_chekhov принимает значение 1, значит речь о рассказе Чехова, а если принимает значение 0, то о рассказе Зощенко. Если вставить нашу переменную в регрессионную формулу получится следующее:

[y_i = hatbeta_0 + hatbeta_1 times text{dummy_chekhov} + epsilon_i,]

Так как dummy_chekhov принимает либо значение 1, либо значение 0, то получается, что модель предсказывает лишь два значения:

[y_i = left{begin{array}{ll}hatbeta_0 + hatbeta_1 times 1 + epsilon_i = hatbeta_0 + hatbeta_1 + epsilon_itext{, если рассказ Чехова}\
hatbeta_0 + hatbeta_1 times 0 + epsilon_i = hatbeta_0 + epsilon_itext{, если рассказ Зощенко}
end{array}right.]

Таким образом, получается, что свободный член (beta_0) и угловой коэффициент (beta_1) в регресси с категориальной переменной получает другую интерпретацию. Одно из значений переменной кодируется при помощи (beta_0), а сумма коэффициентов (beta_0+beta_1) дают другое значение переменной. Так что (beta_1) — это разница между оценками двух значений переменной.

Давайте теперь запустим регрессию на этих же данных:

fit2 <- lm(log_ratio~author, data = checkov_zoshenko)
summary(fit2)

Call:
lm(formula = log_ratio ~ author, data = checkov_zoshenko)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.8652 -0.6105 -0.0607  0.6546  3.2398 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept)  -5.0213     0.2120 -23.680 < 0.0000000000000002 ***
authorЧехов  -1.3200     0.2321  -5.687         0.0000000867 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9717 on 125 degrees of freedom
Multiple R-squared:  0.2056,	Adjusted R-squared:  0.1992 
F-statistic: 32.34 on 1 and 125 DF,  p-value: 0.00000008665

Во-первых стоит обратить внимание на то, что R сам преобразовал нашу категориальную переменную в dummy-переменную authorЧехов. Во-вторых, можно заметить, что значения t-статистики и p-value совпадают с результатами полученными нами в t-тесте выше. Статистическти значимый коэффициент при аргументе authorЧехов следует интерпретировать как разницу средних между логарифмом долей в рассказах Чехова и Зощенко.

В работе (Coretta 2017, https://goo.gl/NrfgJm) рассматривается отношения между длительностью гласного и придыхание согласного. Автор собрал данные 5 носителей исландского. Дальше он извлек длительность гласного, после которого были придыхательные и непридыхательные. Скачайте данные и постройте регрессионную модель, предсказывающую длительность гласного на основе .

Множественная регрессия

Множественная регрессия позволяет проанализировать связь между зависимой и несколькими зависимыми переменными. Формула множественной регрессии не сильно отличается от формулы обычной линейной регрессии:

[y_i = hatbeta_0 + hatbeta_1 times x_{1i}+ dots+ hatbeta_n times x_{ni} + epsilon_i,]

  • (x_{ki}) — (i)-ый элемент векторов значений (X_1, dots, X_n);
  • (y_i) — (i)-ый элемент вектора значений (Y);
  • (hatbeta_0) — оценка случайного члена (intercept);
  • (hatbeta_k) — коэфциент при переменной (X_{k});
  • (epsilon_i) — (i)-ый остаток, разница между оценкой модели ((hatbeta_0 + hatbeta_1 times x_i)) и реальным значением (y_i); весь вектор остатков иногда называют случайным шумом.

В такой регресии предикторы могут быть как числовыми, так и категориальными (со всеми вытекающими последствиями, которые мы обсудили в предудщем разделе). Такую регрессию чаще всего сложно визуализировать, так как в одну регрессионную линию вкладываются сразу несколько переменных.

Попробуем предсказать длину лепестка на основе длины чашелистик и вида ириса:

iris %>% 
  ggplot(aes(Sepal.Length, Petal.Length, color = Species))+
  geom_point()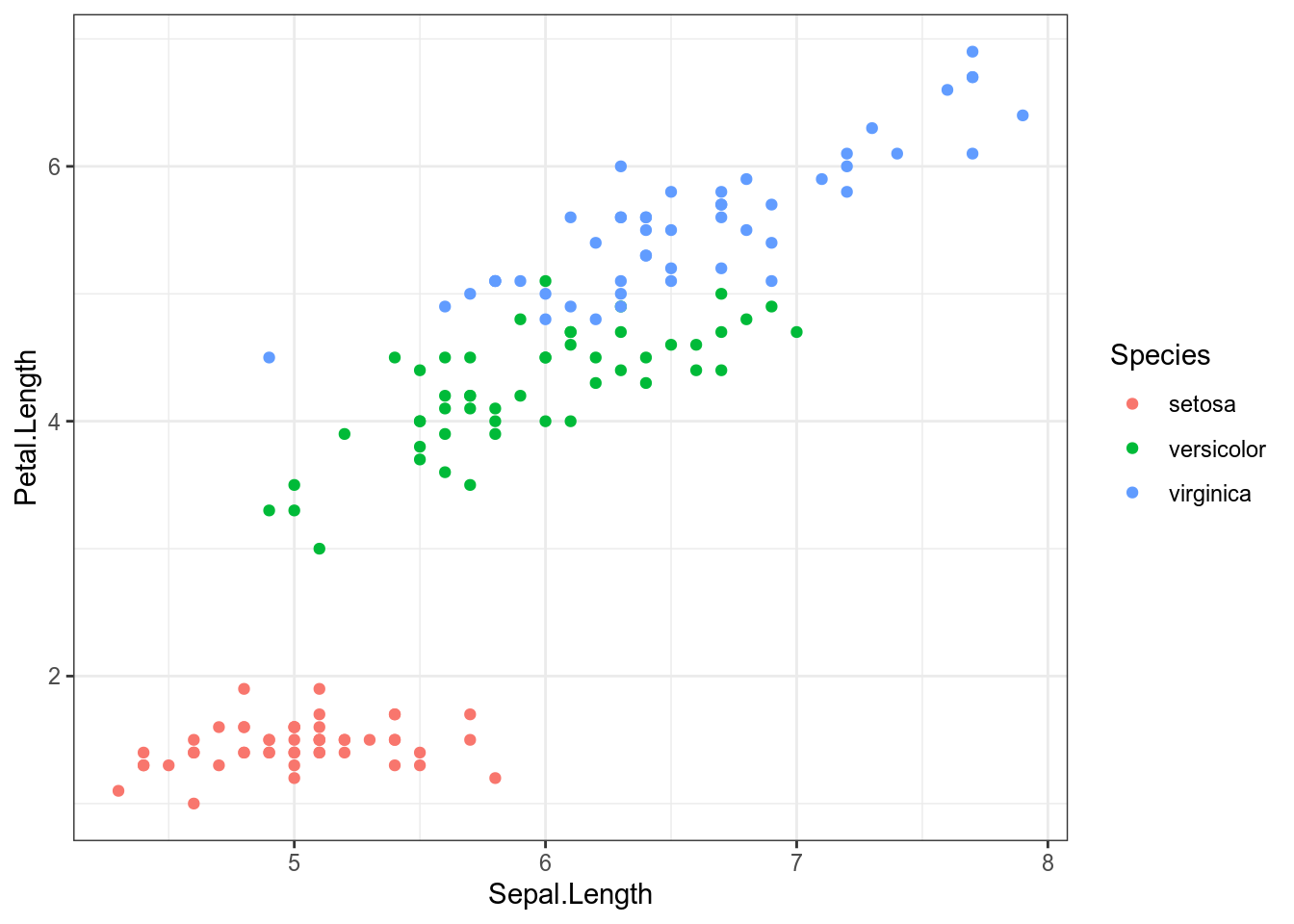

Запустим регрессию:

fit3 <- lm(Petal.Length ~ Sepal.Length+ Species, data = iris)
summary(fit3)

Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value             Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397      0.0000000000101 ***
Sepal.Length       0.63211    0.04527  13.962 < 0.0000000000000002 ***
Speciesversicolor  2.21014    0.07047  31.362 < 0.0000000000000002 ***
Speciesvirginica   3.09000    0.09123  33.870 < 0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,	Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 0.00000000000000022

Все предикторы статистически значимы. Давайте посмотрим предсказания модели для всех наблюдений:

iris %>% 
  mutate(prediction = predict(fit3)) %>% 
  ggplot(aes(Sepal.Length, prediction, color = Species))+
  geom_point()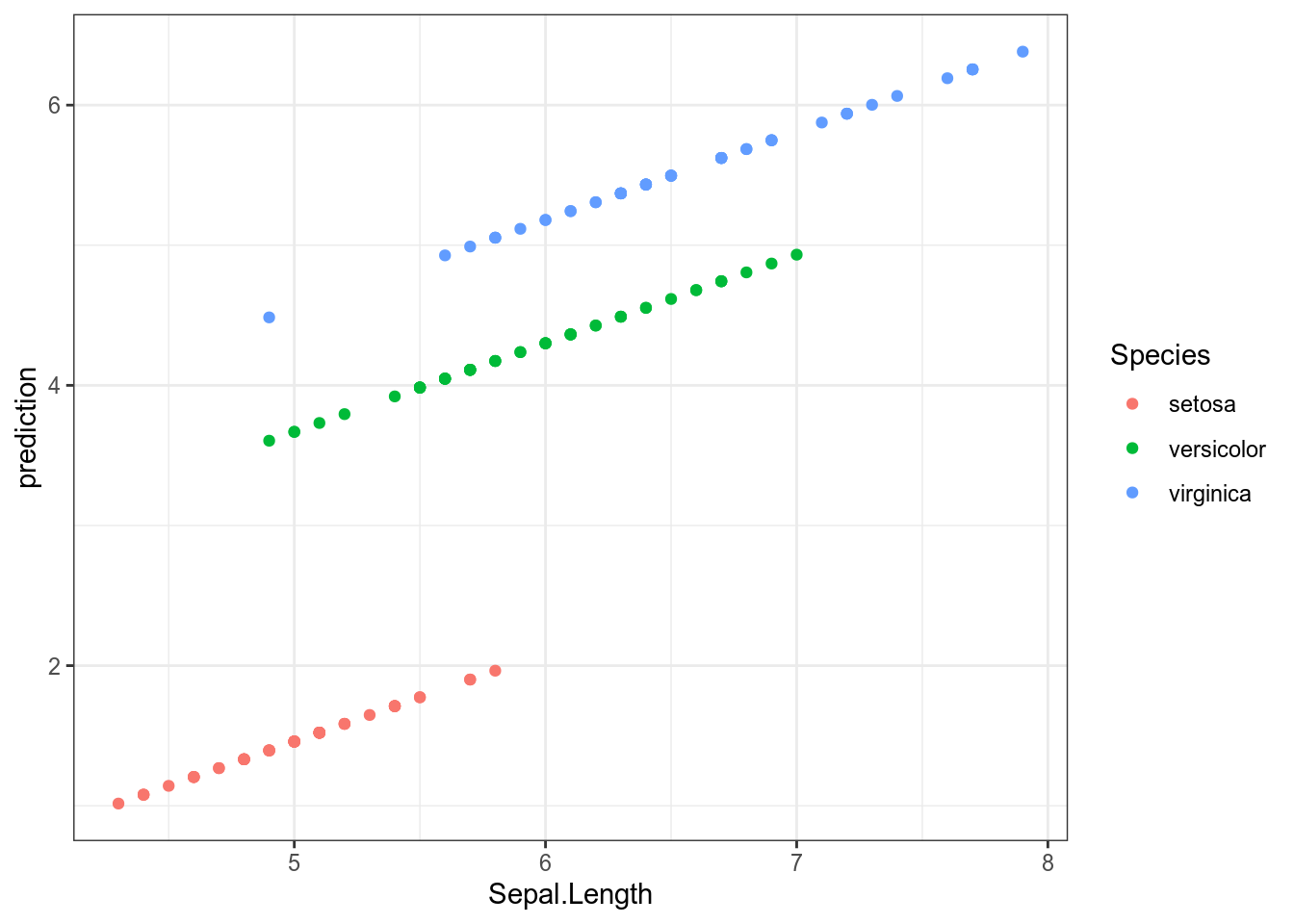

Всегда имеет смысл визуализировать, что нам говорит наша модель. Если использовать пакет ggeffects (или предшествовавший ему пакет effects), это можно сделать не сильно задумываясь, как это делать:

library(ggeffects)
plot(ggpredict(fit3, terms = c("Sepal.Length", "Species")))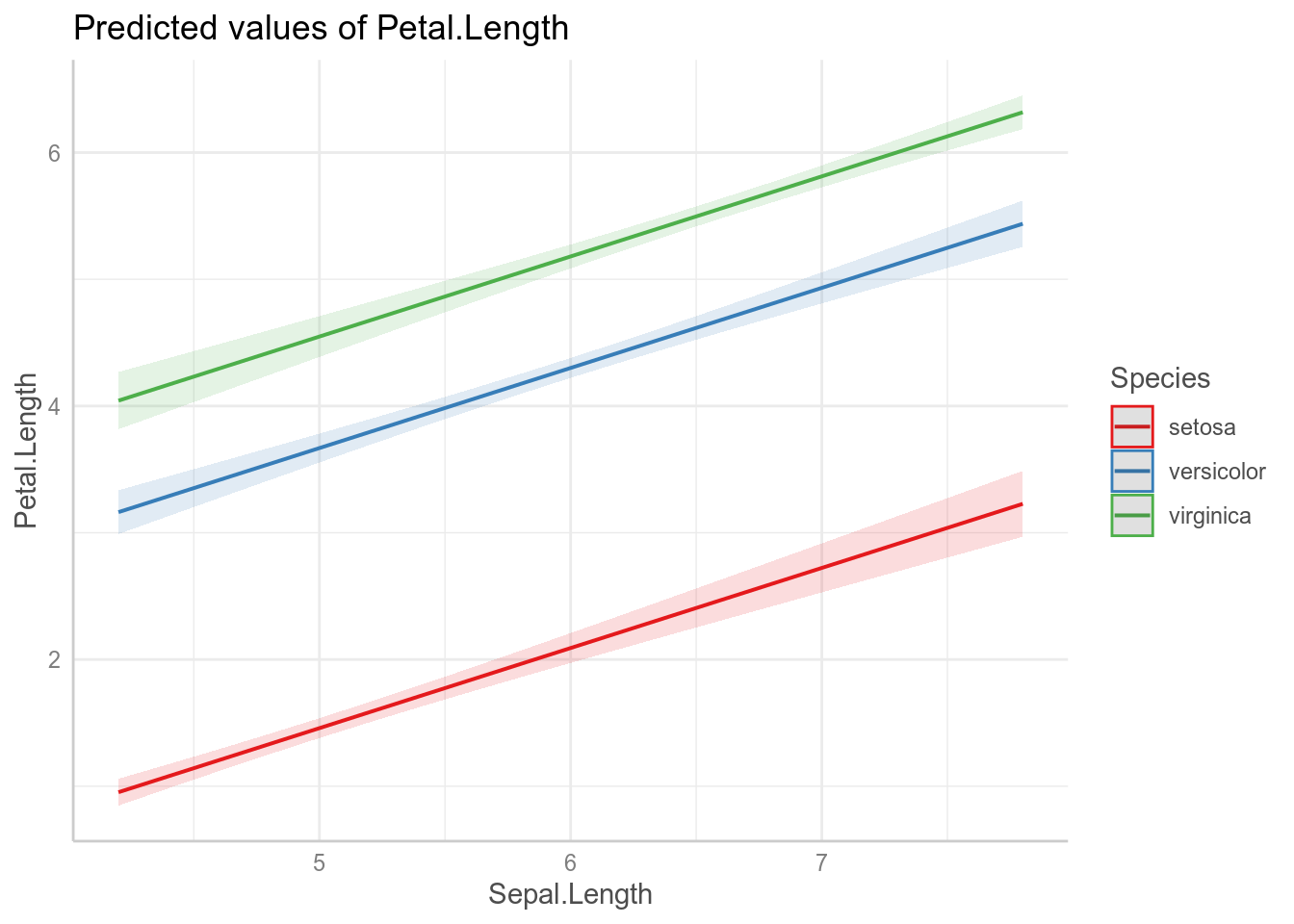

Как видно из графиков, наша модель имеет одинаковые угловые коэффициенты (slope) для каждого из видов ириса и разные свободные члены (intercept).


Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value             Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397      0.0000000000101 ***
Sepal.Length       0.63211    0.04527  13.962 < 0.0000000000000002 ***
Speciesversicolor  2.21014    0.07047  31.362 < 0.0000000000000002 ***
Speciesvirginica   3.09000    0.09123  33.870 < 0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,	Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 0.00000000000000022

[y_i = left{begin{array}{ll} -1.70234 + 0.63211 times text{Sepal.Length} + epsilon_itext{, если вид setosa}\
-1.70234 + 2.2101 + 0.63211 times text{Sepal.Length} + epsilon_itext{, если вид versicolor} \
-1.70234 + 3.09 + 0.63211 times text{Sepal.Length} + epsilon_itext{, если вид virginica}
end{array}right.]

Сравнение моделей

Как нам решить, какая модель лучше? Ведь теперь можно добавить сколько угодно предикторов? Давайте создадим новую модель без предиктора Species:

fit4 <- lm(Petal.Length ~ Sepal.Length, data = iris)
  • можно сравнивать статистическую значимость предикторов
  • можно сравнивать (R^2)
summary(fit3)$adj.r.squared
[1] 0.9743786
summary(fit4)$adj.r.squared
[1] 0.7583327
  • чаще всего используют так называемые информационные критерии, самый популярный – AIC (Akaike information criterion). Сами по себе значение этого критерия не имеет значения – только в сравнении моделей, построенных на похожих данных. Чем меньше значение, тем модель лучше.

Послесловие

  • сущетсвуют ограничения на применение линейной регресии
    • связь между предсказываемой переменной и предикторами должна быть линейной
    • остатки должны быть нормально распределены (оценивайте визуально)
    • дисперсия остатков вокруг регрессионной линии должно быть постоянно (гомоскидастично)
    • предикторы не должны коррелировать друг с другом
    • все наблюдения в регрессии должны быть независимы друг от друга

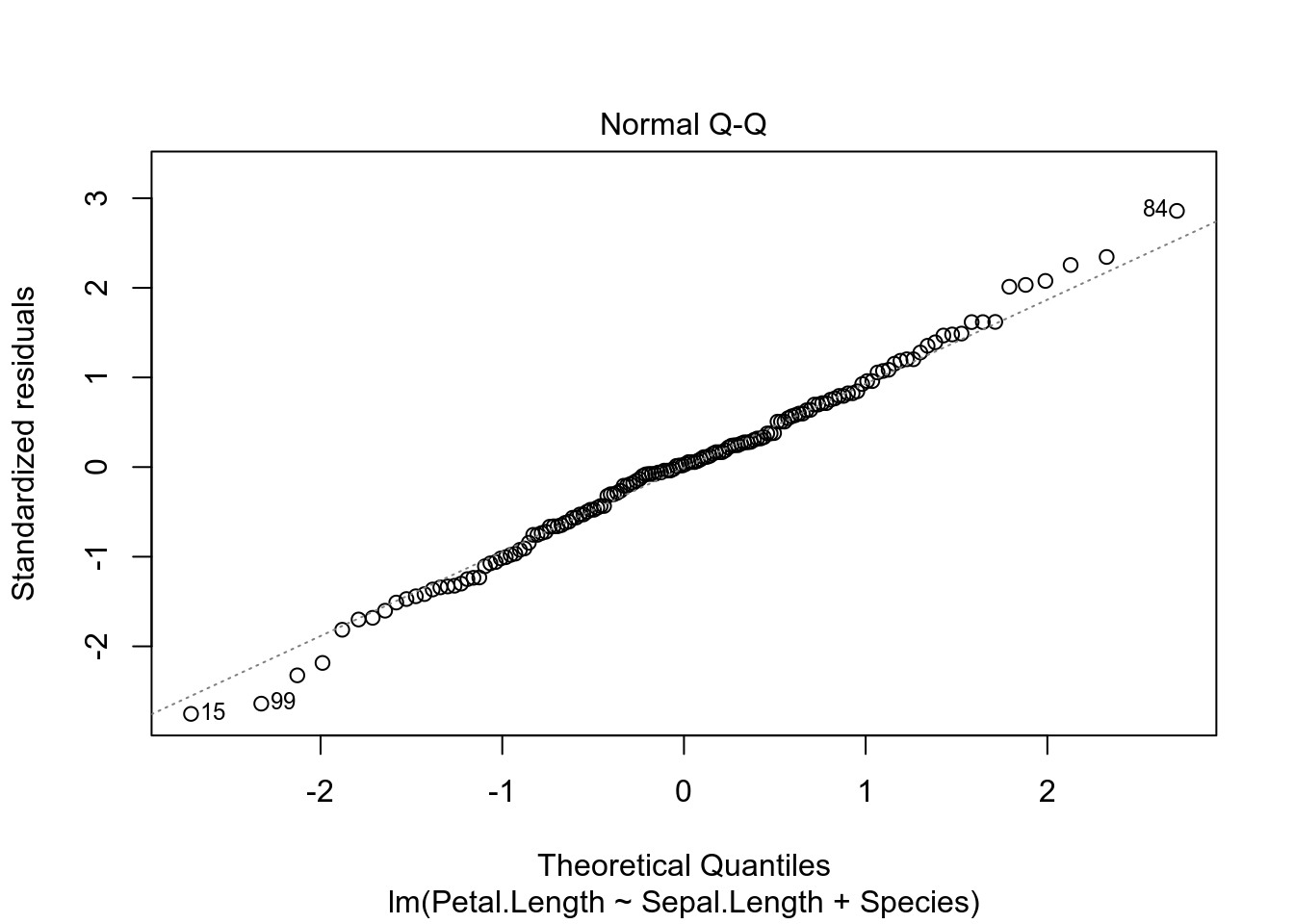
Вот так вот выглядят остатки нашей модели на основе датасета iris. Смотрите пост, в котором обсуждается, как интерпретировать график остатков.

plot(fit3, which=c(1, 2))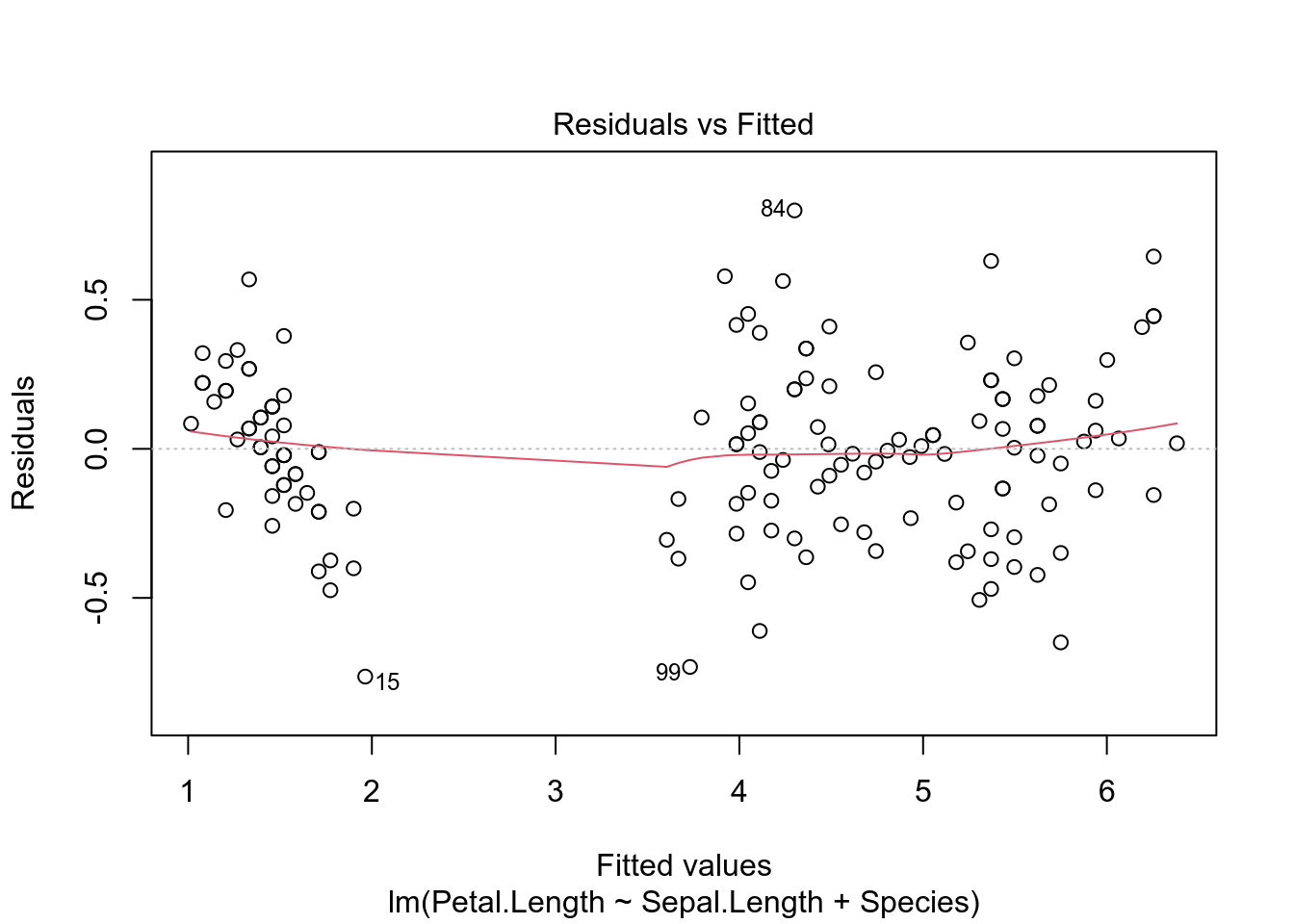

  • сущетсвуют трюки, позволяющие автоматически отбирать модели (см. функцию step())
  • существует достаточно большое семейство регрессий, который зависят от типа независимой (предсказываемой) переменной или ее распределения
    • логистическая (если предсказываемая переменная имеет два возможных исхода)
    • мультиномиальная (если предсказываемая переменная имеет больше двух возможных дискретных исхода)
    • нелиненые регресии (если связь между переменными нелинейна)
    • регрессия со смешанными эффектами (если внутри данных есть группировки, т. е. наблюдения не независимы)
    • и другие.
Источник

R Programming Language is an open-source programming language that is widely used as a statistical software and data analysis tool. R generally comes with the Command-line interface. R is available across widely used platforms like Windows, Linux, and macOS. R language provides very easy methods to calculate the average, variance, and standard deviation.

Average in R Programming

Average a number expressing the central or typical value in a set of data, in particular the mode, median, or (most commonly) the mean, which is calculated by dividing the sum of the values in the set by their number. The basic formula for the average of n numbers x1, x2, ……xn is

A = (x_1 + x_2 ........ + x_n)/ n

Example:

Suppose there are 8 data points,

2, 4, 4, 4, 5, 5, 7, 9

The average of these 8 data points is,

A = frac{2 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5

Computing Average in R Programming

To compute the average of values, R provides a pre-defined function mean(). This function takes a Numerical Vector as an argument and results in the average/mean of that Vector.

Syntax: mean(x, na.rm)

Parameters:

  • x: Numeric Vector
  • na.rm: Boolean value to ignore NA value

Example 1:

R

list = c(2, 4, 4, 4, 5, 5, 7, 9)

print(mean(list))

 Output:

[1] 5

Example 2:

R

list = c(2, 40, 2, 502, 177, 7, 9)

print(mean(list))

 Output:

[1] 105.5714

Variance in R Programming Language

Variance is the sum of squares of differences between all numbers and means. The mathematical formula for variance is as follows,
Formula: sigma^{2}= frac { sum_{i=1}^{N} (x_{i}-mu)^{2}}{N}

where,

mu , is, Mean,

N is the total number of elements or frequency of distribution. 

Example:

Let’s consider the same dataset that we have taken in average. First, calculate the deviations of each data point from the mean, and square the result of each,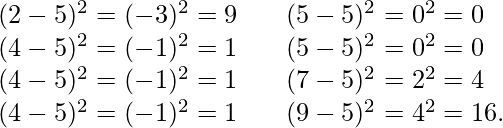
begin{array}{lll} (2-5)^2 = (-3)^2 = 9 && (5-5)^2 = 0^2 = 0 \ (4-5)^2 = (-1)^2 = 1 && (5-5)^2 = 0^2 = 0 \ (4-5)^2 = (-1)^2 = 1 && (7-5)^2 = 2^2 = 4 \ (4-5)^2 = (-1)^2 = 1 && (9-5)^2 = 4^2 = 16. \ end{array} [Tex]variance = frac{9 + 1 + 1 + 1 + 0 + 0 + 4 + 16}{8} = 4[/Tex]

Computing Variance in R Programming

One can calculate the variance by using var() function in R.

Syntax: var(x)

Parameters:

x: numeric vector

Example 1:

R

list = c(2, 4, 4, 4, 5, 5, 7, 9)

print(var(list))

 Output:

[1] 4.571429

Example 2:

R

list = c(212, 231, 234, 564, 235)

print(var(list))

 Output:

[1] 22666.7

Standard Deviation in R Programming Language

Standard Deviation is the square root of variance. It is a measure of the extent to which data varies from the mean. The mathematical formula for calculating standard deviation is as follows,  
Standard Deviation = sqrt{ variance }

Example:

Standard Deviation for the above data,
Standard Deviation = sqrt{ 4 } = 2

Computing Standard Deviation in R

One can calculate the standard deviation by using sd() function in R.

Syntax: sd(x)

Parameters:

x: numeric vector

Example 1:

R

list = c(2, 4, 4, 4, 5, 5, 7, 9)

print(sd(list))

 Output:

[1] 2.13809

Example 2:

R

list = c(290, 124, 127, 899)

print(sd(list))

 Output:

[1] 367.6076

Last Updated :
16 Dec, 2021

Like Article

Save Article

Источник
×

Post on:

Twitter

Facebook

Google+

Or copy & paste this link into an email or IM:

Источник

  • Редакция Кодкампа

17 авг. 2022 г.
читать 1 мин

Дисперсия — это способ измерить , насколько разбросаны значения данных вокруг среднего значения.

Формула для нахождения дисперсиинаселения :

σ 2 = Σ (xi – μ) 2 / N

где μ — среднее значение совокупности, x i — i -й элемент совокупности, N — размер совокупности, а Σ — просто причудливый символ, означающий «сумма».

Формула для нахождения дисперсии выборки :

s 2 = Σ (x i – x ) 2 / (n-1)

где x — среднее значение выборки, x i — i -й элемент в выборке, а n — размер выборки.

Пример: расчет выборки и дисперсии генеральной совокупности в R

Предположим, у нас есть следующий набор данных в R:

#define dataset
data <- c(2, 4, 4, 7, 8, 12, 14, 15, 19, 22)

Мы можем рассчитать выборочную дисперсию , используя функцию var() в R:

#calculate sample variance
var(data)

[1] 46.01111

И мы можем рассчитать дисперсию населения , просто умножив дисперсию выборки на (n-1)/n следующим образом:

#determine length of data
n <- length (data)

#calculate population variance
var(data) * (n-1)/n

[1] 41.41

Обратите внимание, что дисперсия генеральной совокупности всегда будет меньше дисперсии выборки.

На практике мы обычно рассчитываем выборочные дисперсии для наборов данных, поскольку сбор данных для всей совокупности является необычным.

Пример. Расчет выборочной дисперсии нескольких столбцов

Предположим, у нас есть следующий фрейм данных в R:

#create data frame
data <- data.frame(a=c(1, 3, 4, 4, 6, 7, 8, 12),
 b=c(2, 4, 4, 5, 5, 6, 7, 16),
 c=c(6, 6, 7, 8, 8, 9, 9, 12))

#view data frame
data

 a b c
1 1 2 6
2 3 4 6
3 4 4 7
4 4 5 8
5 6 5 8
6 7 6 9
7 8 7 9
8 12 16 12

Мы можем использовать функцию sapply() для вычисления выборочной дисперсии каждого столбца во фрейме данных:

#find sample variance of each column
sapply(data, var)

 a b c 
11.696429 18.125000 3.839286

И мы можем использовать следующий код для вычисления выборочного стандартного отклонения каждого столбца, который представляет собой просто квадратный корень из выборочной дисперсии:

#find sample standard deviation of each column
sapply(data, sd)

 a b c 
3.420004 4.257347 1.959410

Вы можете найти больше руководств по R здесь .

Источник

Добавить комментарий