Как найти дисперсию воспроизводимости

Лекция
4

а)
Дисперсия воспроизводимости при
различном количестве параллельных
опытов.

б)
Дисперсия воспроизводимости при
одинаковом количестве параллельных
опытов.

г)
Контрольные вопросы.

Дисперсия
воспроизводимости характеризует ошибки
параллельных опытов, т.е. опытов
проведенных в одном режиме, но в разное
время.

Так, если проведено
m
параллельных опытов и получен ряд
значений выходных величин

Y₁,
Y₂,
Y₃,
…, Y_m,
т.е. выборка случайной величины Y_i,
то дисперсию воспроизводимости вычисляют
по формуле:

, (3.13)

где m
– количество параллельных опытов;

Y_i
– значение
выходной величины Y;

–
математическое ожидание Y.

Дисперсия
воспроизводимости является важным
показателем, характеризующим уровень
«шума» на установке.

На практике часто
возникают ситуации, когда необходимо
вычислить общую дисперсию воспроизводимости
всего эксперимента. При этом различают
случаи, когда вычисляют дисперсию
воспроизводимости при различном и при
одинаковом количестве параллельных
опытов.

1. Дисперсия воспроизводимости при различном количестве параллельных опытов.

Предположим,
анализируется n
проб какого-то химического вещества.
При анализе каждой пробы производится
различное количество параллельных
опытов m₁,
m₂,
m₃,…,
m_n

Таблица
3.1- Матрица планирования экспериментов

№ пробы	Результаты параллельных опытов	Количество параллельных опытов
Y1	Y2	Y3	. . . . .	Ym
1 2 3 . . . n	Y11 Y21 Y31 . . . Yn1	Y12 Y22 . . . Yn2	Y23 Y33 . . . Yn3	. . . . . . . . . . . . . . . . . . . .	Y1m Y2m Y3m . . . Ynm	m1 m2 m3 . . . mn	Y1 Y2 Y3 . . . Yn	S12 S22 S32 . . . Sn2

1. Вычисляем построчное
   (частное) математическое ожидание для
   каждого опыта:

,
(3.14)

где m_i
– количество параллельных опытов в
каждой строке.

1. Вычисляем построчные
   (частные) дисперсии:

, (3.15)

1. Проверяем
   однородность построчных дисперсий по
   критерию Фишера (F),
   т.к. различное количество параллельных
   опытов в каждой строке (m_i).

, (3.16)

где F_табл
– табличный критерий, который находим
по степеням свободы числителя и
знаменателя (f),
они равны f
= m_i
– 1.

Если F_р<
F_табл,
то дисперсии однородны и можно вычислять
общую дисперсию воспроизводимости. В
противном случае дисперсии не однородны.
В этом случае надо проверить анормальность
результатов в строке с максимальной
дисперсией, исключить грубые ошибки и
повторить проверку однородности
построчных дисперсий.

4)
Общая дисперсия воспроизводимости всех
опытов будет равна средневзвешенному
значению построчных дисперсий:

, (3.17)

где S_i²
– значения построчных дисперсий;

f_i
– степени свободы построчных дисперсий.

Общая степень
свободы (f_воспр):

, (3.18)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Совокупность действий, связанных с составлением уравнения регрессии, называется регрессионным анализом. Регрессионный анализ результатов однофакторного эксперимента включает в себя следующие действия:

1) подбор вида уравнения регрессии. Осуществляется с помощью, например, функциональных шкал;

2) определение постоянных коэффициентов в уравнении регрессии. Осуществляется с помощью МНК;

3) проверку соответствия (адекватности) уравнения регрессии результатам опытов.

Проверка адекватности уравнения регрессии результатам опытов проводится следующим образом:

1) По результатам повторных изменений в каждом опыте вычисляются дисперсия функции отклика (σ_у²), среднеквадратичная погрешность (), доверительный интервал 9), математическое ожидание ().

2) Осуществляется проверка однородности дисперсии , где j = 1,2,…, N – число опытов. Дисперсии  называются однородными, если при неограниченном увеличении числа повторных измерений п в каждом из опытов они стремятся к общему пределу, т.е.

.

Дисперсии проверяются на однородность с помощью критериев Фишера, Кохрена, Бартлета. Наиболее просто осуществить проверку однородности с помощью критерия Фишера. Для этого из всех дисперсий () выбирают две: наибольшую () и наименьшую ().

Отношение / сравнивают с табличным значением критерия Фишера (F):

· если /< F – дисперсии  и  однородны, следовательно, однородны и все дисперсии, лежащие в промежутке <<;

· если /> F – дисперсии неоднородны.

Значения критерия Фишера берутся из таблицы 2.3, составленной при доверительной вероятности Р = 0,95, для числа степеней свободы числителя (дисперсии ) и числа степеней свободы знаменателя (дисперсии ).

Таблица 2.3

fзнам	fчисл
1	2	3	4	5	6	12	24	∞
1 2 3 4 5 6 7 8 9 10 12 24 ∞	164,4 18,5 10,1 7,7 6,6 6,0 5,6 5,3 5,1 5,0 4,8 4,3 3,8	199,5 19,2 9,6 6,9 5,8 5,1 4,7 4,5 4,3 4,7 3,9 3,4 3,0	215,7 19,2 9,3 6,6 5,4 4,8 4,4 4,1 3,9 3,7 3,5 3,0 2,6	224,6 19,3 9,1 6,4 5,2 4,5 4,1 3,8 3,6 3,5 3,3 2,8 2,4	230,2 19,3 9,0 6,3 5,1 4,4 4,0 3,7 3,5 3,3 3,1 2,6 2,2	234,9 19,3 8,9 6,2 5,0 4,3 3,9 3,6 3,4 3,2 3,0 2,5 2,1	244,9 19,4 8,7 5,9 4,7 4,0 3,6 3,3 3,1 2,9 2,7 2,2 1,8	249,0 19,5 8,6 5,8 4,5 3,8 3,4 3,1 2,9 2,7 2,5 2,0 1,5	254,3 19,5 8,5 5,6 4,4 3,7 3,2 2,9 2,7 2,5 2,3 1,7 1,0

Если в каждом из опытов число повторных измерений одинаково и равно п, то f_числ = f_знам = п – 1.

Если дисперсии  и неоднородны, то это означает, что число повторных измерений недостаточно или что среди результатов повторных измерений опыта с дисперсией находится промах.

Следует очистить результаты повторных измерений от промахов, увеличить число повторных измерений, снова определить  и проверить их однородность. Если все дисперсии  и однородны, можно переходить к следующему действию.

3) Вычисляется дисперсия воспроизводимости (S²_воспр). Дисперсия воспроизводимости – это среднее из дисперсий () всех опытов. Дисперсия воспроизводимости характеризует средний разброс результатов повторных измерений во всех опытах относительно своих математических ожиданий.

Если в каждом опыте число повторных измерений одинаково и равно п, то S²_воспр определяется по формуле:

S²_воспр =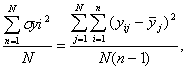

где N – число опытов,  – математическое ожидание в j-м опыте. Если в опытах число повторных измерений различно, то S²_воспр определяется как средневзвешенная величина

S²_воспр =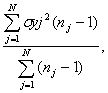

где – число повторных измерений в j–м опыте.

Число степеней свободы дисперсии воспроизводимости равно сумме чисел степеней свободы дисперсий опытов:

.

4) Вычисляется дисперсия адекватности (S²_ад). Дисперсия адекватности – это сумма квадратов отклонений расчётных и экспериментальных значений функции отклика в каждом опыте, отнесённая к числу степеней свободы. Она характеризует разброс экспериментальных результатов относительно расчётных и определяется по формуле:

S²_ад =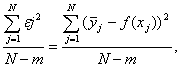

где т – число постоянных коэффициентов в уравнении регрессии;  — математическое ожидание в j–м опыте; N – m = f_ад – число степеней свободы дисперсии адекватности;

3) Проверяется однородность дисперсий адекватности и воспроизводимости. Дисперсии адекватности и воспроизводимости будут однородными, если их отношение будет меньше табличного значения критерия Фишера:

S²_ад / S²_воспр < F,

где значения F берутся (см. табл. 2.3)для числа степеней свободы числителя (дисперсии адекватности) и числа степеней свободы знаменателя (дисперсия воспроизводимости).

Если дисперсии S²_ад и S²_воспр однородны , то с доверительной вероятностью Р = 0,95 можно утверждать, что составленное уравнение регрессии адекватно. Это следует из того, что при и  разброс экспериментальных значений функции отклика относительно её расчётных значений равен среднему разбросу результатов повторных измерений в каждом опыте относительно своих математических ожиданий.

Если S²_ад / S²_воспр > F, то выбранное уравнение регрессии неадекватно. Следует перейти к уравнению регрессии более высокого порядка или выбрать уравнение регрессии другого вида, определить значения коэффициента и снова проверить адекватность.

Если опыты состоят из однократных измерений, то адекватность уравнения регрессии не может быть проверена изложенным способом. В этом случае проверка адекватности уравнения регрессии может быть осуществлена сравнением доверительного интервала функции отклика (а_у) с отклонениями расчётных и экспериментальных значений функции отклика (). Очевидно, что, если < а_у, то уравнение регрессии адекватно.

Обработка
результатов эксперимента

Тщательное, скрупулезное
выполнение эксперимента, несомненно, является главным условием успеха исследо­вания.
Это общее правило, и планирование эксперимента не относится к исключениям.

Однако нам не безразлично,
как обработать полученные данные. Мы хотим навлечь из них всю информацию и сде­лать
соответствующие выводы. Как всегда, мы находимся между Сциллой и Харибдой. С
одной стороны, не извлечь из эксперимента все, что из него следует,– значит
прене­бречь нелегким трудом экспериментатора. С другой стороны, сделать
утверждения, не следующие из эксперимента, – значит создавать иллюзии,
заниматься самообманом.

Статистические методы
обработки результатов позво­ляют нам не перейти разумной меры риска.

Метод наименьших
квадратов

Нач­нем с простого случая:
один фактор, линейная модель. Интересующая нас функция отклика (которую мы
будем также называть уравнением регрессии) имеет вид

Это хорошо известное
уравнение прямой линии. Наша цель – вычисление неизвестных коэффициентов b₀ и b₁. Мы провели эксперимент, чтобы использовать при вычис­лениях его
результаты. Как это сделать наилучшим обра­зом?

Если бы все экспериментальные
точки лежали строго на прямой линии, то для каждой из них было бы справед­ливо
равенство

,

где i = 1, 2, …, N – номер опыта. Тогда не было бы никакой проблемы. На практике это равенство
нарушается и вместо него приходится писать

,

где  – разность между экспериментальным и вычис­ленным по
уравнению регрессии значениями y в i-й экспе­риментальной точке. Эту величину иногда невязкой.

Мы хотим найти такие
коэффициенты регрессии, при которых невязки будут минимальны. Это требо­вание
можно записать по-разному. В зависимости от этого мы будем получать разные
оценки коэффициентов. Вот одна из возможных записей

,

которая приводит к методу
наименьших квадратов.

Когда мы ставим эксперимент,
то обычно стремимся провести больше (во всяком случае не меньше) опытов, чем
число неизвестных коэффициентов. Поэтому система линейных уравнений

оказывается переопределенной
и часто противоречивой (т. е. она может иметь бесконечно много решений или
может не иметь решений). Переопределенность возникает, когда число уравнений
больше числа неизвестных; противоре­чивость – когда некоторые из уравнений
несовместимы друг с другом.

Только если все
экспериментальные точки лежат па прямой, то система становится определенной и
имеет единственное решение.

МНК обладает тем
замечательным свойством, что он делает определенной любую, произвольную систему
уравнений. Он делает число уравнений равным чис­лу неизвестных коэффициентов.

Для определения двух
неизвестных коэф­фициентов требуется два уравнения. Давайте попробуем их
получить.

Мини­мум некоторой
функции, если он существует, достигается при одновременном равенстве нулю
частных производных по всей неизвестным, т. е.

.

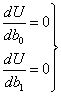В явном виде это
запишется как

,

.

Окончательные формулы для
вычисления коэффи­циентов регрессии, которые удобно находить с помощью
определителей, имеют вид

,

.

Величина  называется остаточной суммой квадратов ( – значение параметра оптимизации,
вычисленное из уравнения регрессии). МНК гарантирует, что эта величина минимально возможная.

Обобщение на многофакторный
случай не связано с какими-либо принципиальными трудностями.

Воспользуемся тем, что
матрицы планирования ортогональны и нормированы, т.е.

       и         

Для любого числа факторов коэффициенты
будут вычисляться по формуле

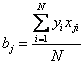
В этой формуле j = 0, 1, 2 …, k – номер фактора. Ноль записан для вычисления
b₀.

Так как каждый фактор (кроме x₀) варьируется
на двух уровнях +1 и –1, то вычисления сводятся к приписыванию столбцу y знаков соответствующего фактору столбца и
алгебраическому сложению полученных значений. Де­ление результата на число
опытов в матрице планирова­ния дает искомый коэффициент.

Регрессионный
анализ

До сих пор мы
пользовались МНК как вычисли­тельным приемом. Нам нигде не приходилось
вспоминать о статистике. Но, как только мы начинаем про­верять какие-либо
гипотезы о пригодности модели или о значимости коэффициентов, приходится
вспоминать о статистике. И с этого момента МНК превращается в рег­рессионный
анализ.

А регрессионный анализ как
всякий статистический метод, применим при определенных предположениях,
постулатах.

Первый постулат. Параметр оптимизации y есть случайная величина с нормальным законом распределения.
Дисперсия воспроизводимости – одна из харак­теристик этого закона
распределения.

В данном случае, как и по
отношению к любым другим постулатам, нас интересуют два вопроса: как проверить
его выполнимость и к чему приводят его нарушения?

При наличии большого
экспериментального материала (десятки параллельных опытов) гипотезу о
нормальном рас­пределении можно проверить стандартными статистичес­кими тестами
(например, – критерием). К сожалению, экспериментатор редко
располагает такими данными, поэтому приходится принимать этот постулат на веру.

При нарушении нормальности мы
лишаемся возмож­ности установления вероятностей, с которыми справедливы те или
иные высказывания. В этом таится большая опас­ность. Мы рискуем
загипнотизировать себя численными оценками и вероятностями, за которыми ничего не
стоит. Вот почему надо очень внима­тельно относиться к возможным нарушениям
предпосылок.

Второй постулат. Дисперсия y не зависит от
абсо­лютной величины y. Выполнимость этого постулата проверяется
с помощью критериев однородности дисперсий в разных точках фак­торного
пространства. Нарушение этого постулата недо­пустимо.

Всегда существует та­кое
преобразование y, которое делает дисперсии одно­родными. Увы, его не всегда
легко найти. Довольно часто помогает логарифмическое преобразование, с которого
обычно начинают поиски.

Третий постулат. Значения факторов суть неслу­чайные величины.
Это несколько неожиданное утверждение практически означает, что установление
каждого фактора на заданный уровень и его поддержание существенно точнее, чем
сшибка воспроизводимости.

Нарушение этого постулата
приводит к трудностям при реализации матрицы планирования. Поэтому оно обычно
легко обнаруживается экспериментатором.

Существует еще четвертый
постулат, налагающий ог­раничения на взаимосвязь между значениями факторов. У
Нас он выполняется автоматически в силу ортогональ­ности матрицы планирования.

Проверка адекватности модели

Первый вопрос, который нас
интересует после вычис­ления коэффициентов модели, это проверка ее пригод­ности.
Мы будем называть такую проверку провер­кой адекватности модели.

Для характеристики среднего
разброса относительно линии регрессии вполне подходит остаточная сумма квад­ратов.
Неудобство состоит в том, что она зависит от чис­ла коэффициентов в
уравнении: введите столько коэф­фициентов, сколько вы провели независимых
опытов, и получите остаточную сумму, равную нулю. Поэтому предпочитают относить
ее на один «свободный» опыт. Число таких опытов называется числом степеней
свобо­ды f.

Числом степеней свободы в
статистике называется разность между числом опытов и числом коэффициентов
(констант), которые уже вычислены по результатам этих опытов независимо друг от
друга.

Остаточная сумма квадратов,
деленная на число сте­пеней свободы, называется остаточной диспер­сией, или
дисперсией адекватности

.

В статистике разработан
критерий, который очень удобен для проверки гипотезы об адекватности модели. Он
называется F-критерием Фишера и определяется сле­дующей
формулой:

.

 – это дисперсия воспроизводимости со своим числом степеней
свободы.

Удобство использования
критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с
табличным значением.

Если рассчитанное значение F-критерия не превы­шает табличного, то, с соответствующей
доверительной вероятностью, модель можно считать адекватной. При превышении
табличного значения эту приятную гипотезу приходится отвергать.

Этот способ расчета дисперсии
адекватности, подходит, если опыты в матрице планирования не дублируются, а
информация о дисперсии воспроизводимости извлекается из параллельных опытов в
нулевой точке или из предварительных экспериментов.

Важны два случая: 1) опыты во
всех точках плана дублируются одинаковое число раз (равномерное дублирование),
2) число параллельных опытов не одинаково (неравномерное дублирование).

В первом случае дисперсию
адекватности нужно умножать на n,
где n – число повторных опытов

 .

Такое видоизменение
формулы вполне естественно. Чем больше число параллельных опытов, тем с большей
достоверностью оцени­ваются средние значения. Поэтому требования к различиям
между экспериментальными и расчетными значениями становятся более жесткими, что
отражается в увеличении F-критерия.

Во втором случае, когда приходится иметь
дело с неравномер­ным дублированием, положение усложняется. Даже когда экспе­риментатор
задумал провести равное число параллельных опытов, часто не удается по тем или
иным причинам все их реализовать. Кроме того, иногда приходится отбрасывать
отдельные опыты как выпадающие наблюдения.

При неравномерном дублировании нарушается
ортогональность матрицы планирования и, как следствие, изменяются расчетные фор­мулы
для коэффициентов регрессии и их ошибок, а также для дис­персии адекватности.

Для дисперсии
адекватности можно записать общую формулу

,

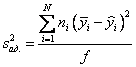где N – число
различных опытов (число строк матрицы);

n_i
– число параллельных опытов в i-й
строке матрицы;

 – среднее арифметическое из n_i параллельных
опытов;

 – предсказанное по уравнению значение в этом опыте.

Смысл этой формулы
очень прост: различию между эксперимен­тальным и расчетным значением придается
тем больший вес, чем больше число повторных опытов.

Для b-коэффициентов
нельзя записать универсальную рас­четную формулу. Все зависит от того, какой
был план и как дубли­ровались опыты. Всякий раз приходится делать специальные
рас­четы, пользуясь методом наименьших квадратов.

Проверка значимости коэффициентов

Проверка значимости каждого
коэффициента прово­дится независимо.

Ее можно осуществлять двумя
равноценными спосо­бами: проверкой по t-критерию Стьюдента или построе­нием доверительного интервала. При
использовании пол­ного факторного эксперимента или регулярных дробных реплик
доверительные интервалы для всех коэффициен­тов (в том числе и эффектов
взаимодействия) равны друг другу.

Прежде всего, надо найти
дисперсию коэф­фициента регрессии . Она
определяется в нашем по формуле

Из формулы видно, что
дисперсии всех коэффициентов равны друг другу, так как они зависят только от
ошибки опыта и числа опытов.

Теперь легко построить доверительный
интервал

Здесь t – табличное значение
критерия Стьюдента при числе степеней свободы, с которыми определялась , и выбранном уровне значимости (обычно 0,05);  – квадратичная
ошибка коэффициента регрессии.

Коэффициент
значим, если его абсолютная величина больше доверительного интервала.