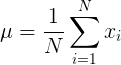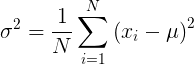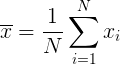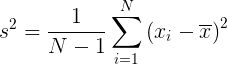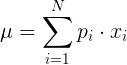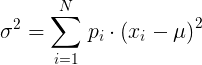Как найти дисперсию выборки онлайн

Онлайн калькулятор для расчета выборочной дисперсии (дисперсия выборки). Выборочная дисперсия‭ ‬-‭ ‬это показатель разброса,‭ ‬наблюдаемого в определенной выборке данных.‭ ‬С вычислительной точки зрения ее можно объяснить как – среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.

Для того, чтобы оценить дисперсию по выборке необходимо:
– Вычислить математические ожидания данных (выборочное среднее – среднее арифметическое значений вариант в выборке).
– Вычитаем математическое ожидание из исходного значения для всех данных из выборки и возводим результат в квадрат.
– Складываем все полученные в предыдущем шаге значения и делим сумму на N-1.

Онлайн-калькулятор дисперсии поможет вам определить дисперсию, сумму квадратов и коэффициент дисперсии для определенного набора данных. Кроме того, этот калькулятор также отображает среднее значение и стандартное отклонение путем пошагового расчет дисперсии онлайн. Прочтите, чтобы узнать, как найти дисперсию онлайн и стандартное отклонение, используя формулу выборочной дисперсии.

Что такое дисперсия?

Дисперсия группы или набора чисел – это число, которое представляет «разброс» набора. Формально это квадрат отклонения набора от среднего и квадрат стандартного отклонения.

Другими словами, небольшая дисперсия означает, что точки данных имеют тенденцию быть близкими к среднему и очень близко друг к другу. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения и друг от друга. Дисперсия – это среднее значение квадрата расстояния от каждой точки до среднего.

Типы дисперсии:

Вариация выборки: дисперсия выборки не охватывает всю возможную выборку (случайная выборка людей).

Дисперсия населения: дисперсия, которая измеряется для всего населения (например, всех людей).

Однако онлайн-калькулятор стандартного отклонения позволяет определить стандартное отклонение (σ) и другие статистические измерения данного набора данных.

Формулы отклонения:

Формула дисперсии совокупности

дисперсия формула (совокупности):

Дисперсия (обозначается как σ2) выражается как среднеквадратическое отклонение от среднего для всех точек данных. Мы пишем:

$$ σ2 = ∑ (xi – μ) ^ 2 / N $$

где,

• σ2 – дисперсия;
• μ – среднеквадратическое значение; а также
• xᵢ представляет i-ю точку данных среди N общих точек данных.

Вы можете рассчитать его с помощью калькулятора дисперсии генеральной совокупности, в противном случае есть три шага для оценки дисперсии:

• Чтобы найти разницу между средним значением точки, используйте формулу: xi – μ
• Теперь возьмите в квадрат разницу между средним значением каждой точки: (xi – μ) ^ 2
• Затем найдите среднее квадратическое отклонение от среднего: ∑ (xi – μ) ^ 2 / N.

Это дисперсия формула совокупности.

Пример формулы отклонения

Уравнение выборки дисперсии имеет следующий вид:

s2 = ∑ (xi – x̄) 2 / (N – 1)

где,

s2 – оценка дисперсии;

x – выборочное среднее; а также

xi – i-я точка данных среди N общих точек данных.

Как рассчитать дисперсию?

Чтобы найти среднее значение данного набора данных. Подставьте все значения и разделите на размер выборки n.

ni = 1x дюйм x = ∑ i = 1 nx дюйм

Теперь найдите среднюю разницу значений данных, вам нужно вычесть среднее значение данных и возвести результат в квадрат.

(хи – х) ^ 2 (хи – х) ^ 2

Затем вычислите квадратичные разности и сумму квадратов всех квадратичных разностей.

S = ∑ I = 1n (xi – x) ^ 2

Итак, найдите дисперсию, дисперсия формула генеральной совокупности:

Дисперсия = σ ^ 2 = Σ (xi – μ) ^ 2

Уравнение дисперсии набора данных выборки:

Дисперсия = s ^ 2 = Σ (xi – x) ^ {2n − 1}

Эти формулы запоминать не нужно. Чтобы вам было удобно, наш примерный калькулятор дисперсии выполняет все расчет дисперсии онлайн, связанные с дисперсией, автоматически, используя их.

Тем не менее, Калькулятор диапазона среднего среднего значения режима поможет вам рассчитать средний средний режим и диапазон для введенного набора данных.

Пример расчета

Давайте посчитаем дисперсию оценок пяти студентов на экзамене: 50, 75, 89, 93, 93. Выполните следующие действия:

• Найдите среднее

Чтобы найти среднее значение (x), разделите сумму всех этих значений на количество точек данных:

х = (50 + 75 + 89 + 93 + 93) / 5

х̄ = 80

• Вычислите разницу между средним значением и квадратом отличий от среднего. Следовательно, среднее значение равно 80, мы используем формулу для вычисления разницы от среднего:

xi – x̄

Первая точка – 50, поэтому разница от среднего составляет 50 – 80 = -30.

Квадрат отклонения от среднего – это квадрат предыдущего шага:

(xi – x̄) 2

Итак, квадрат отклонения равен:

(50 – 80) 2 = (-30) 2 = 900

В приведенной ниже таблице квадрат отклонения рассчитан на основе среднего значения всех результатов испытаний. Столбец «Среднее отклонение» – это результат минус 30, а столбец «Стандартное отклонение» – это столбец перед квадратом.

Счет	Отклонение от среднего	Квадратное отклонение
50	-30	900
75	-5	25
89	9	81
93	13	169
93	13	169

• Рассчитайте стандартное отклонение и дисперсию

Затем используйте квадраты отклонений от среднего:

σ2 = ∑ (xi – x̄) 2 / N

σ2 = (900 + 25 + 81 + 169 + 169) / 5

σ2 = 268,5

дисперсия случайной величины онлайн результатов экзамена составила 268,8.

Как работает калькулятор дисперсии?

Онлайн-калькулятор дисперсии совокупности вычисляет дисперсию для заданных наборов данных. Вы можете просмотреть работу, проделанную для расчет дисперсии онлайн из набора данных, следуя этим инструкциям:

Вход:

• Сначала введите значения набора данных через запятую.
• Затем выберите дисперсию для выборки или совокупности.
• Нажмите кнопку «Рассчитать», чтобы получить результаты.

Выход:

• Калькулятор дисперсии выборки отображает дисперсию, стандартное отклонение, количество, сумму, среднее значение, коэффициент дисперсии и сумму квадратов.
• Этот калькулятор также обеспечивает пошаговые вычисления дисперсии, коэффициента дисперсии и стандартного отклонения.

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:

В чем разница между стандартным отклонением и дисперсией?

Дисперсия – это квадрат отклонения от среднего, а стандартное отклонение – это квадратный корень из числа. Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).

Значение высокой дисперсии – это плохо или хорошо?

Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией обычно выгодны для агрессивных инвесторов с меньшим неприятием риска, в то время как акции с низкой дисперсией обычно выгодны для консервативных инвесторов с более низкой толерантностью к риску.

Каков диапазон отклонений?

Диапазон – это разница между высоким и низким значением. Поскольку используются только крайние значения, потому что эти значения будут сильно на него влиять. Чтобы найти диапазон отклонения, возьмите максимальное значение и вычтите минимальное значение.

Заключение:

Воспользуйтесь этим онлайн-калькулятором дисперсии, который работает как с выборкой, так и с наборами данных о генеральной совокупности, используя формулу генеральной и выборочной дисперсии. Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.

Other Languages: Variance Calculator, Varyans Hesaplama,  Calculadora De Variancia, Kalkulator Varians, Kalkulator Wariancji, Výpočet Rozptylu, 分散 計算.

калькулятор выборочной дисперсии

формула:

где,
σ = выборочная дисперсия
Х = входное значение
μ = Среднее
N = количество баллов

Sample Variance Calculator

Given here is the free online Sample Variance Calculator to calculate the sample variance for the given set of data which is applied in sample and population statistics. It is defined as measuring how much a sample differ from each other in a range of sample values.

Given here is the free online Sample Variance Calculator to calculate the sample variance for the given set of data which is applied in sample and population statistics. It is defined as measuring how much a sample differ from each other in a range of sample values.

Formula:

Where,
σ = Sample Variance
X = Input Value
μ = Mean
N = Number of Scores

Use our free online sample variance calculator to measure how each number in a set is far from the mean. Sample variance refers to variation of the data points in a single sample. A sample is a selected number of items taken from a population. It is calculated by taking the differences between each number in the set and the mean, squaring the differences and dividing the sum of the squares by the number of values in the set. In short Sample Variance is used to calculate how varied a sample is. In this online sample variance calculator enter the values separated by a comma and you get the variance for the given range of data.

Калькулятор отклонений

Калькулятор дисперсии и способы ее расчета.

Калькулятор дисперсии совокупности и выборочной дисперсии

Калькулятор дисперсии дискретных случайных величин

Введите вероятность или вес и номер данных в каждой строке:

Расчет дисперсии всего населения

Средняя численность населения:

Дисперсия населения:

Расчет дисперсии выборочных данных

Выборочное среднее:

Выборочная дисперсия:

Расчет дисперсии дискретной случайной величины

Среднее значение случайной величины:

Дисперсия случайной переменной:

---

Смотрите также

• Дисперсия
• Калькулятор стандартного отклонения
• Калькулятор средневзвешенного значения
• Калькулятор GPA
• Математические калькуляторы