Как найти дисперсию выборки по таблице

Для того чтобы охарактеризовать
рассеяние наблюдаемых значений
количественного признака выборки вокруг
своего среднего значения ,
вводят сводную
характеристику – выборочную дисперсию.

Выборочной дисперсией

называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения .

Если все значения x₁,
х₂,
…, x_n
признака выборки объема п
различны, то

.

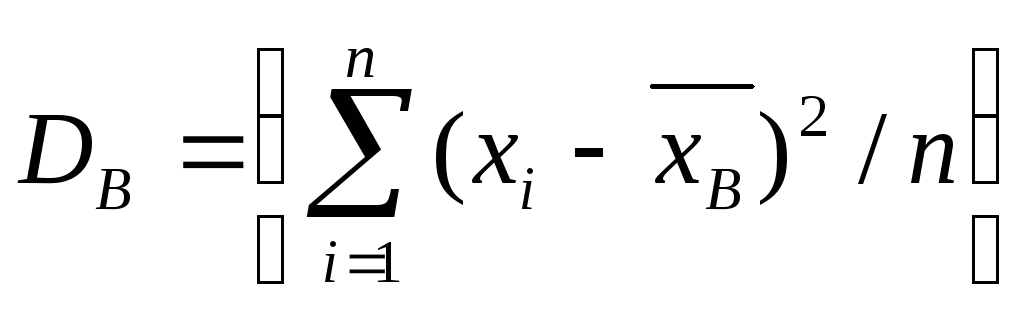Если же значения признака
x₁,
х₂,
…, x_k
имеют соответственно
частоты п₁,
n₂,…,
n_k,
причем n₁
+ n₂+…+n_k
= n, то

,

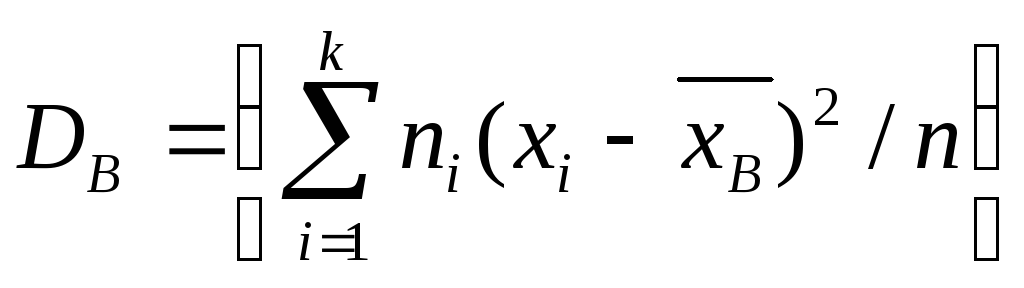т.е. выборочная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.

Пример.
Выборочная
совокупность задана таблицей распределения

x_i

1
2 3 4

n_i
20 15
10
5

Найти выборочную
дисперсию.

Решение.
Найдем выборочную среднюю (см. § 4):

.

Найдем выборочную
дисперсию:

.

Кроме дисперсии для характеристики
рассеяния значений признака выборочной
совокупности вокруг своего среднего
значения пользуются сводной
характеристикой-средним квадратическим
отклонением.

Выборочным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из выборочной дисперсии:

.

§ 10. Формула для вычисления дисперсии

Вычисление дисперсии, безразлично-выборочной
или генеральной, можно упростить,
используя следующую теорему.

Теорема. Дисперсия
равна среднему квадратов значений
признака минус квадрат общей средней:

.

Доказательство. Справедливость теоремы
вытекает из преобразований:

.

Итак,

,

где
,.

Пример.
Найти
дисперсию по данному распределению

x_i
1
2 3 4

n_i
20
15
10
5

Решение.
Найдем
общую среднюю:

.

Найдем
среднюю квадратов
значений признака:

.

Искомая дисперсия

=5-2²=1.

§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на k
групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти групповую
среднюю (см. § 6) и дисперсию значений
признака, принадлежащих группе,
относительно групповой средней.

Групповой дисперсией называют
дисперсию значений признака, принадлежащих
группе, относительно групповой средней

,

где n_i
–
частота значения
x_i;
j –
номер группы;

– групповая средняя
группы j;
–
объем группыj.

Пример
1. Найти
групповые дисперсии совокупности,
состоящей из следующих двух групп:

первая группа		вторая группа
	xi	ni			xi	ni
2	1	3	2
4	7	8	3
5	2

Решение.
Найдем
групповые средние:

;

.

Найдем
искомые
групповые дисперсии:

;

.

Зная дисперсию каждой группы, можно
найти их среднюю арифметическую.

Внутригрупповой дисперсией называют
среднюю арифметическую дисперсий,
взвешенную по объемам групп:

,

где N_j
– объем группы
j;
п =–
объем всей совокупности.

Пример
2.
Найти
внутригрупповую дисперсию по данным
примера 1.

Решение.
Искомая внутригрупповая дисперсия
равна

Зная групповые средние и общую среднюю,
можно найти дисперсию групповых средних
относительно общей средней.

Межгрупповой дисперсией называют
дисперсию групповых средних относительно
общей средней:

,

где
–
групповая средняя группыj;
N_j
– объем группы j;

– общая средняя;
n
=–
объем всей совокупности.

Пример
3. Найти
межгрупповую дисперсию по

данным
примера 1.

Решение.
Найдем общую среднюю:

.

Используя
вычисленные выше величины
=
4,=
6, найдем искомую межгрупповую дисперсию:

.

Теперь целесообразно ввести специальный
термин для дисперсии всей совокупности.

Общей дисперсией называют дисперсию
значений признака всей совокупности
относительно общей средней:

,

где n_i
– частота значения
x_i
;
–
общая средняя; n
– объем всей совокупности.

Пример
4. Найти
общую дисперсию по данным примера 1.

Решение.
Найдем искомую общую дисперсию, учитывая,
что общая средняя равна 14/3:

Замечание.
Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:

D_общ=
148/45;

D_внгр
+ D_межгр=
12/5 + 8/9= 148/45.

В следующем
параграфе будет доказано, что такая
закономерность справедлива для любой
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

---

Дисперсия — это способ измерения разброса значений в наборе данных.

Формула для расчета дисперсии населения :

σ 2 = Σ (xi – μ) 2 / N

куда:

• Σ : символ, означающий «сумма».
• μ : Среднее значение населения
• x i : i -й элемент из совокупности
• N : Численность населения

Формула для расчета выборочной дисперсии :

s 2 = Σ (x i – x ) 2 / (n-1)

куда:

• x : выборочное среднее
• x i : i -й элемент из выборки
• n : размер выборки

Мы можем использовать формулы VAR.S() и VAR.P() в Excel, чтобы быстро вычислить выборочную дисперсию и дисперсию генеральной совокупности (соответственно) для заданного набора данных.

В следующих примерах показано, как использовать каждую функцию на практике.

Пример 1: Расчет выборочной дисперсии в Excel

На следующем снимке экрана показано, как использовать функцию VAR.S() для расчета выборочной дисперсии значений в столбце A:

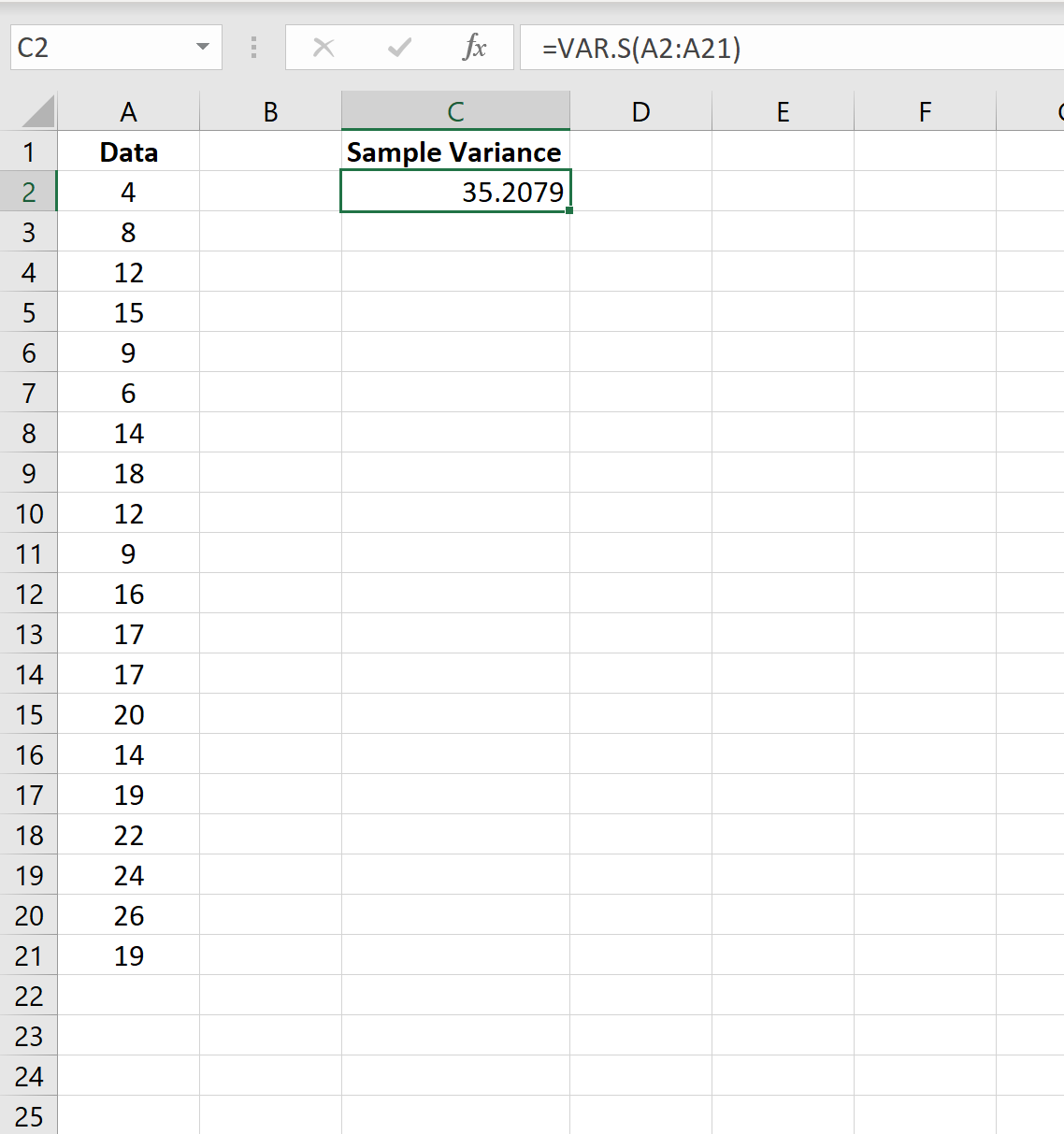
Выборочная дисперсия оказывается равной 35,2079 .

Пример 2: Расчет дисперсии населения в Excel

На следующем снимке экрана показано, как использовать функцию VAR.P() для расчета дисперсии совокупности значений в столбце A:

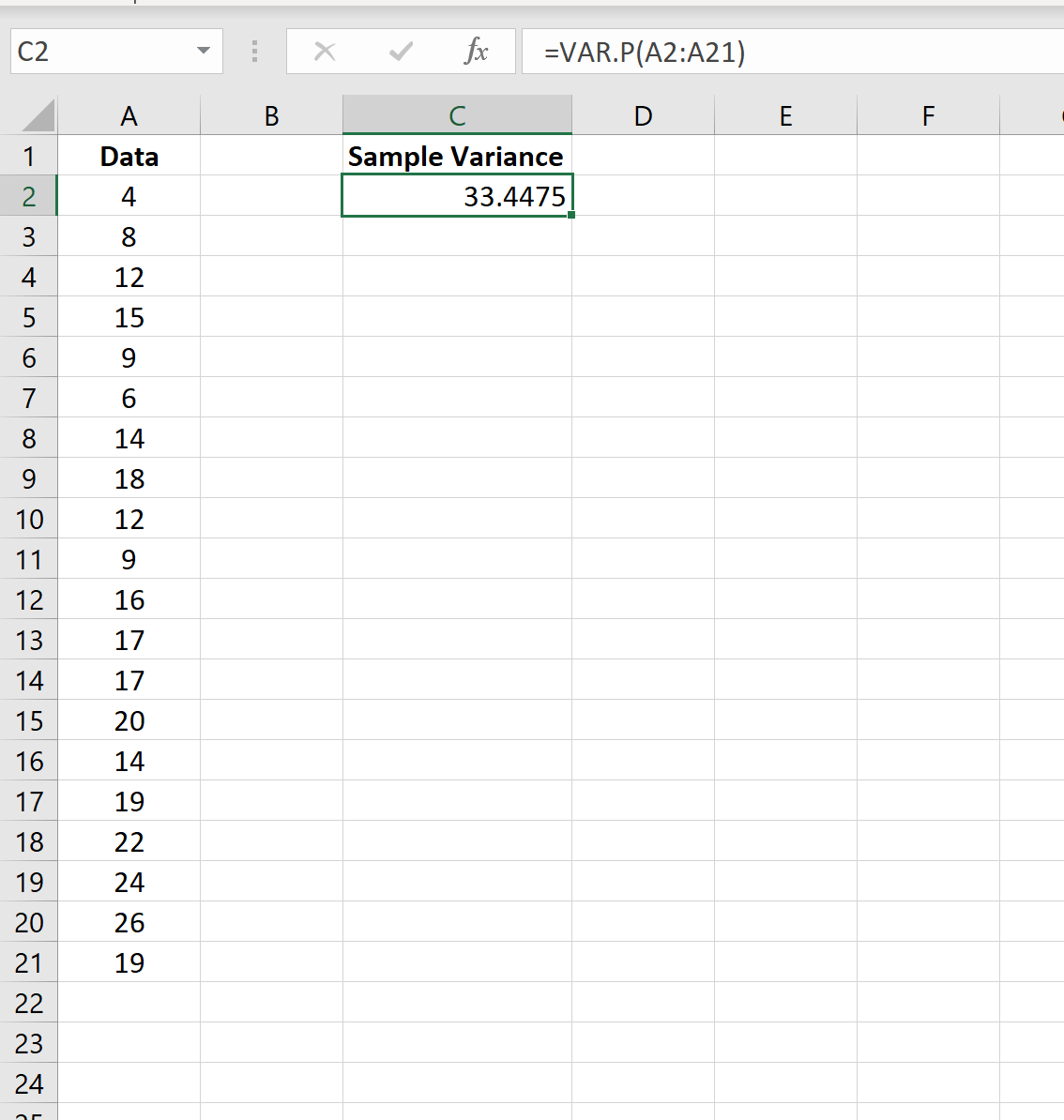
Дисперсия населения оказывается равной 33,4475 .

Примечания по расчету выборки и дисперсии генеральной совокупности

При расчете дисперсии выборки и генеральной совокупности следует учитывать следующее:

• Вы должны вычислить дисперсию совокупности , когда набор данных, с которым вы работаете, представляет всю совокупность, то есть каждое значение, которое вас интересует.
• Вы должны рассчитать выборочную дисперсию , когда набор данных, с которым вы работаете, представляет собой выборку, взятую из большей интересующей совокупности.
• Выборочная дисперсия набора данных всегда будет больше, чем дисперсия генеральной совокупности для того же набора данных, потому что при расчете дисперсии выборки больше неопределенности, поэтому наша оценка дисперсии будет больше.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать другие показатели спреда в Excel:

Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать взвешенное стандартное отклонение в Excel
Как рассчитать коэффициент вариации в Excel

Как найти дисперсию?

Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.

Другие задачи с решениями по ТВ

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку “Вычислить”.
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.

Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Дисперсия, виды и свойства дисперсии

Понятие дисперсии

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

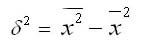
2. Взвешенная дисперсия (для вариационного ряда):

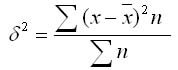
где n — частота (повторяемость фактора Х)

Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

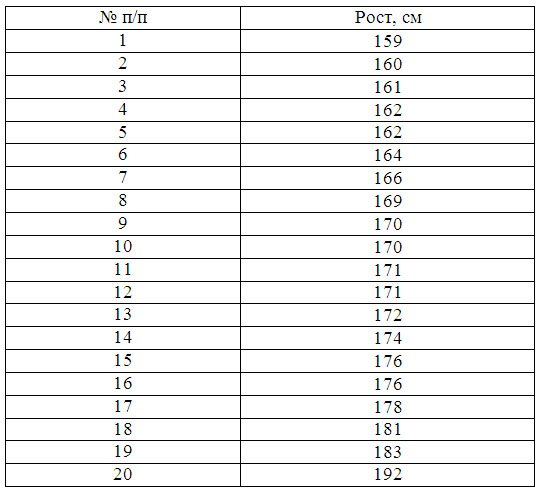
Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:

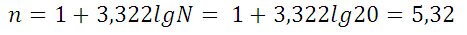
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

Составим интервальную группировку

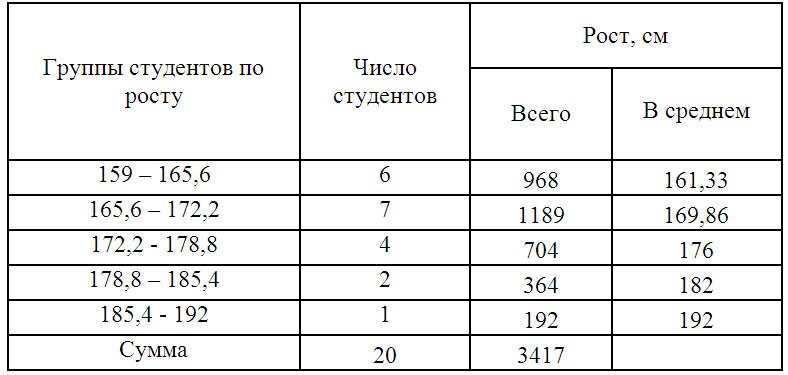
Для дальнейших расчетов построим вспомогательную таблицу:

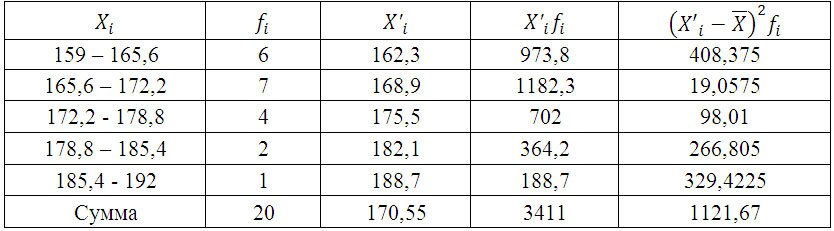
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

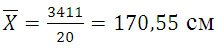
Определим дисперсию по формуле:

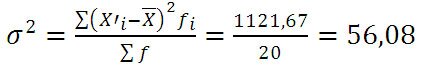
Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии

Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице

Пример 4. Нахождение дисперсии в дискретном ряду

Формулу дисперсии можно преобразовать так:

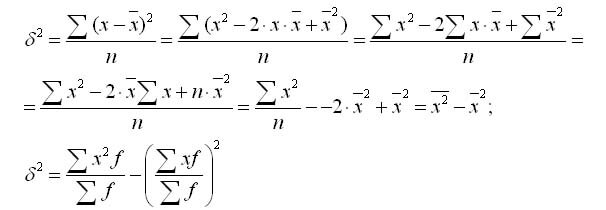
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:

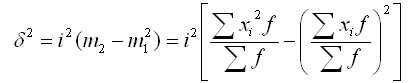
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

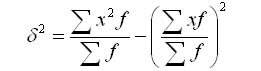
Подставляя в данную формулу дисперсии q =1- р, получаем:

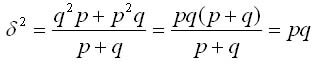
Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

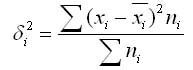
где хi — групповая средняя;
ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

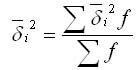
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

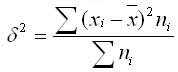
Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

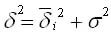
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Была ли эта статья полезной?