Как найти дисперсию заработной платы

          

Номер задачи: S-60

Решение: бесплатно

Распределение населения по заработной плате в бюджетной сфере характеризуется следующими данными: 

Сфера	Средняя заработная плата, тыс. руб.	Количество опрошенных людей, чел	Стандартное отклонение заработной платы, тыс.руб.
Медицинские услуги	25	80	7
Образовательные услуги	20	120	8

Определите:

• общую дисперсию заработной платы, среднее квадратическое отклонение, применяя правила сложения дисперсий;

• коэффициент вариации, рассчитанный по всей совокупности.

Правило сложения дисперсий

Пример решения задачи

---

Задача

Имеются
данные о фонде месячной заработной платы и средней зарплаты одного рабочего по
трем цехам.

Цех	Средняя месячная зарплата одного рабочего (у.е.)	Фонд зарплаты (у.е.)	СКО по зарплате (у.е.)
1	148	41200.7	3000
2	150	51290.4	2100
3	151	41530.5	4900

Требуется:

• Определить среднюю зарплату одного рабочего по предприятию в целом.
• Общую дисперсию по зарплате.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Вычисление средней

1)
Среднюю заработную плату вычислим по формуле средней гармонической:

где

 – фонд заработной платы в

 цехе

 – средняя заработная плата в

 цехе

Вычисление средней внутригрупповой и межгрупповой дисперсий

2)
Вычислим общую дисперсию, пользуясь правилом сложения дисперсий:

Внутригрупповые
дисперсии найдем как квадрат среднего квадратического отклонения (СКО) по
зарплате:

Вычислим
количество рабочих в цеху, разделив фонд заработной платы на среднюю месячную
заработную плату по цеху:

Средняя
из внутригрупповых дисперсий:

Рассчитаем
межгрупповую дисперсию:

Согласно
правилу сложения дисперсий:

Вывод к задаче

Таким
образом средняя заработная плата по трем цехам составила 149,685 у.е. при общей
дисперсии заработной платы

.

Распределение рабочих по заработной плате

Заработная плата, тыс. р.	Число рабочих, fi , чел.	Середина интервала, xi, тыс. р.
1	2	3	4	5	6
До 3,0	2	2	3	6	18
3,0  5,0	12	4	2	24	48
5,0  7,0	15	6	1	15	15
7,0  9,0	64	8	0	0	0
9,0  11,0	55	10	1	55	55
11,0  13,0	32	12	2	64	128
Свыше 13,0	20	14	3	60	180
Итого	200			134	444

Определить дисперсию
и среднее квадратическое отклонение
заработной платы рабочих способом
моментов.

Решение

При использовании
способа моментов расчет дисперсии
осуществляется по формуле

где
m₁,
m₂

моменты первого и второго порядка

Расчет числителей
моментов при А = 8 тыс. р. (значение
заработной платы, имеющее наибольшую
частоту) и h = 2 тыс. р.
(величина интервала группировок) приведен
в графах 46 табл.
3.4.

Момент первого
порядка

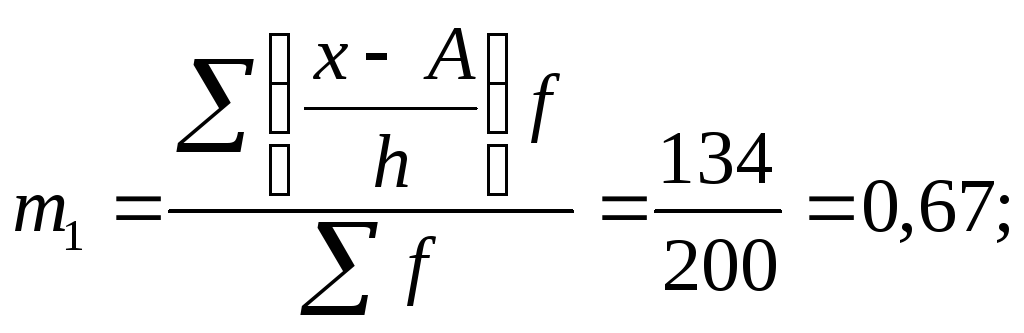
момент
второго порядка

дисперсия
заработной платы

среднее
квадратическое отклонение заработной
платы

Задача
3.4

На предприятии
работает 2000 человек, из них 1600 
мужчины.

Определить дисперсию
и среднее квадратическое отклонение
доли мужчин на предприятии.

Решение

1. Доля мужчин на предприятии

доля
женщин

2.
Дисперсия доли мужчин

среднее
квадратическое отклонение доли мужчин

Задача
3.5

Данные о численности
официально зарегистрированных безработных
и численности экономически активного
населения в Северо-Западном Федеральном
округе на конец июня 2004 г. [23]
приведены в графах 1, 2 табл. 3.5.

Таблица 3.5

Основные показатели регистрируемого рынка труда в Северо-Западном Федеральном округе на конец июня 2004 г.

Территория	Численность официально зарегистрированных безработных, Nбj , тыс. чел.	Численность экономически активного населения, Nаj , тыс. чел.	Уровень регистрируемой безработицы, pj , %
А	1	2	3
Республика Карелия	10,8	400,0	2,7
Республика Коми	14,3	595,8	2,4
Архангельская область	14,9	745,0	2,0
Ненецкий автономный округ	1,1	25,0	4,4
Вологодская область	11,1	652,9	1,7
Калининградская область	7,9	493,8	1,6
Ленинградская область	8,5	850,0	1,0
Мурманская область	18,8	569,7	3,3
Новгородская область	3,9	354,5	1,1
Псковская область	9,3	372,0	2,5
г. Санкт-Петербург	17,0	2428,6	0,7
Итого	117,6	7487,3	

Определить дисперсию
доли безработных в Северо-Западном
Федеральном округе на основе
средней доли безработных по округу и с
использованием правила сложения
дисперсий.

Решение

1. Уровень регистрируемой
безработицы (доля безработных в
численности экономически активного
населения) рассчитывается по формуле

Результаты расчета
приведены в графе 3 табл. 3.5.

2.
Средняя доля безработных в Северо-Западном
Федеральном округе может быть рассчитана
по следующим формулам:

 средней
агрегатной

 средней
арифметической взвешенной

3.
Общая дисперсия доли безработных в
Северо-Западном Федеральном округе,
разделенном на субъекты РФ, рассчитанная
на основе средней доли безработных

4.
Дисперсия доли альтернативного признака
в группе (групповая дисперсия)
рассчитывается по формуле

где


доля безработных, зарегистрированных
в j-м
субъекте РФ;

 доля
занятых в j-м
субъекте РФ.

Например,
дисперсия доли безработных по республике
Карелия

Результаты расчета
групповой дисперсии доли безработных
по всем субъектам РФ в Северо-Западном
Федеральном округе приведены в графе
4 табл. 3.6.

5.
Данные для расчета внутригрупповой и
межгрупповой дисперсии доли безработных
приведен в графах 5, 6 табл. 3.6.

Внутригрупповая
дисперсия (средняя из групповых дисперсий)
доли безработных

Межгрупповая
дисперсия доли безработных

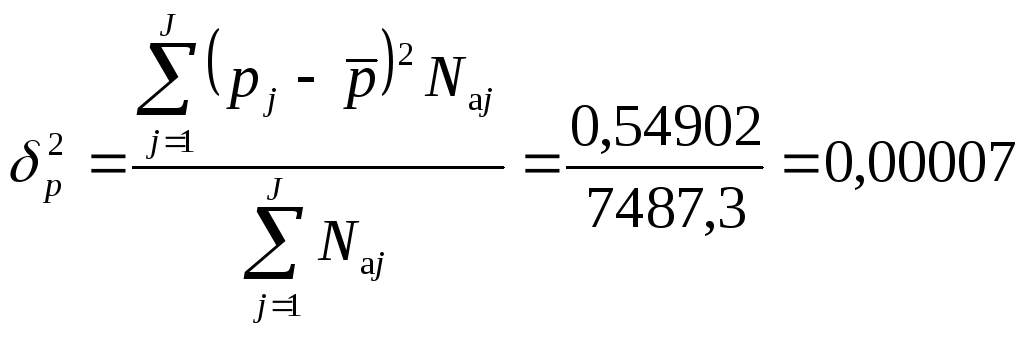
Таблица 3.6

 Готовое решение: Заказ №9520

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Экономика

 Дата выполнения: 21.10.2020

 Цена: 229 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Имеются следующие данные о размере заработной платы рабочих цеха за апрель (табл. 3.33).

Таблица 3.33

Профессия	Число рабочих	Средняя заработная плата, руб.	Внутригрупповая дисперсия заработной платы
Токари	50	4650	6500
Фрезеровщики	25	4800	5025
Слесари	40	4500	4910

Требуется:

1) Определить общую дисперсию заработной платы рабочих цеха;

2) оценить однородность совокупности рабочих цеха по уровню месячной заработной платы;

3) определить, насколько процентов дисперсия в размере заработной платы обусловлена различием в профессии рабочих и влиянием прочих причин.

Сформулировать выводы.

Решение:

1. Определим среднюю заработную плату всех рабочих по формуле средней арифметической взвешенной:

Определим среднюю из внутригрупповых дисперсий по формуле средней арифметической взвешенной:

Определите общую дисперсию заработной платы рабочих цеха; оцените однородность совокупности рабочих цеха по уровню месячной заработной платы.

По каждой из трех основных рабочих профессий цеха (-порядковый номер профессии: 1-токари; 2-фрезеровщики; 3-слесари) имеются соответствующие данные о числе рабочих профессии ( чел.), о средней заработной плате (, руб.), а также о внутригрупповой дисперсии заработной платы (. руб²). Статистические данные за месяц приведены в таблице.

Требуется:

1) определить общую дисперсию заработной платы рабочих цеха;

2) оценить однородность совокупности рабочих цеха по уровню месячной заработной платы;

3) определить, на сколько процентов дисперсия в размере заработной платы обусловлена различиями в профессии рабочих и влиянием других причин.

1	52	2650	2400
2	26	2780	3100
3	42	2420	730

Предварительные сведения.

Для характеристики величины вариации (колеблемости) признака статистической совокупности используются абсолютные и относительные показатели. В качестве абсолютных показателей чаще всего рассматривают дисперсию и среднеквадратическое отклонение (СКО)

,

где – наблюдённые значения признака (варианты), – общее число вариант (объем выборки). Суммирование в этой формуле производится по всем вариантам; – среднее значение признака, – среднее значение квадрата признака

, .

Изучая только общую дисперсию интересующего исследователя признака, нельзя оценить влияние отдельных факторов, как качественных, так и количественных, на величину признака. Это можно сделать при помощи метода группировки, когда варианты подразделяются на непересекающиеся группы по признаку-фактору. При этом, кроме общей средней по всей выборке, рассматриваются средние по отдельным группам и следующие показатели дисперсии:

1. общая дисперсия

2. межгрупповая дисперсия ,

3. внутригрупповые дисперсии ,

4. средняя внутригрупповая дисперсия .

Кратко охарактеризуем эти дисперсии.

1. Общая дисперсия учитывает влияние всех факторов, от которых зависит величина изучаемого признака

, ,

где – общая средняя по всей выборке.

2. Межгрупповая дисперсия (дисперсия групповых средних) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Эта дисперсия определяется по формуле:

,

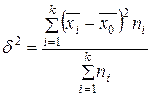здесь – внутригрупповые средние, – число вариант в -ой группе; – число групп, суммирование производится по различным группам.

3. Внутригрупповая дисперсия

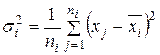
отражает рассеяние значений признака, относящихся к одному уровню группировочного фактора, поэтому она определяется не этим фактором, а другими причинами.

4. Средняя внутригрупповая дисперсия , так же как и , характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия, положенного в основу группировки. Эта дисперсия определяется по формуле

.

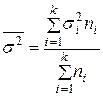Можно доказать, что имеет место правило сложения дисперсий

.

Отношение показывает, какую долю общей дисперсии составляет дисперсия, возникающая под влиянием группировочного фактора, т.е. позволяет оценить влияние этого фактора на величину изучаемого признака .

При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в разных совокупностях используются относительные показатели вариации. Наиболее распространенным среди относительных показателей вариации является коэффициент вариации

%.

Его применяют также и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

Решение:

1. Найдем среднюю из внутригрупповых дисперсий

(руб²)

Определим среднюю зарплату по цеху для основных рабочих профессий (общую среднюю)

(руб.)

Находим межгрупповую дисперсию

(руб²).

Используя правило сложения дисперсий, найдем общую дисперсию заработной платы:

(руб²).

2. Оценим однородность совокупности рабочих цеха по уровню месячной заработной платы с помощью коэффициента вариации

%%.

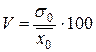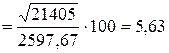Так как %, то совокупность считается однородной.

3. Общая дисперсия заработной платы рабочих цеха обусловлена различиями в профессии на

%%.

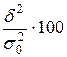Эта же дисперсия обусловлена влиянием других причин на

%%.

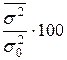Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена – от 99 рублей.