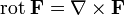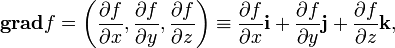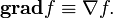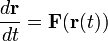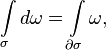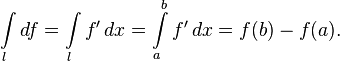Важной
характеристикой векторного поля является
его дивергенция (или расхождение),
которая определяется в каждой точке
области, где задано поле.
Пусть
дано векторное поле в некоторой области
D:
.
Возьмем
произвольную точку
и окружим ее замкнутой поверхностью
(рис. 6.3.7).
В качестве положительной нормали к
поверхности будем считать внешнюю
нормаль.
Поток
в направлении внешней нормали называют
потоком изнутри поверхности.
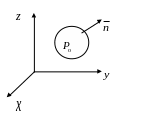
Рис.
6.3.7. Замкнутая поверхность
в произвольном векторном поле

Рис.
6.3.8.
Замкнутая поверхность в потоке жидкости
Пример
4. Представим
мысленно, что замкнутая поверхность
расположена в равномерном потоке текущей
жидкости и жидкость свободно проникает
через ее стенки (рис. 6.3.8).
Поток
изнутри поверхности
будет равен нулю, так как сколько втекает
жидкости в данную поверхность, столько
и вытекает.
Вернемся
к произвольному векторному полю,
заданному в области
.
Найдем количество векторных линий этого
поля, которые возникают в единицу времени
в единице объема
,
заключенного внутри поверхности
.
Очевидно, что оно равно величине потока
изнутри поверхности, деленной на объем,
т.е.
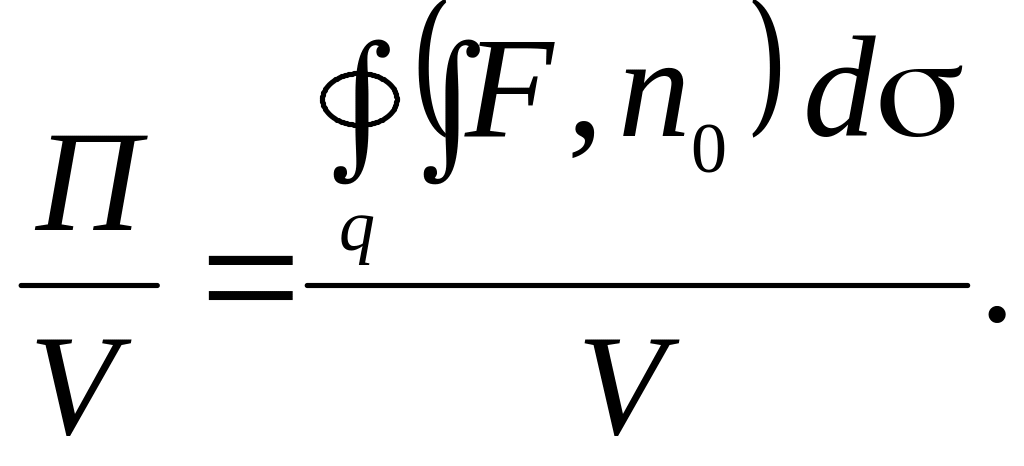
Данное
отношение, определяющее количество
возникающих векторных линий в единице
объема, характеризует среднюю объемную
мощность источника, или мощность стока
(для отрицательных потоков изнутри
поверхности
).
Чтобы
найти, сколько образуется векторных
линий в единицу времени в точке
,
нужно перейти к пределу при
,
т.е. при стягивании объема в точку
.
Предел,
если он существует, называют дивергенцией,
или расхождением векторного поля в
точке
и обозначают
div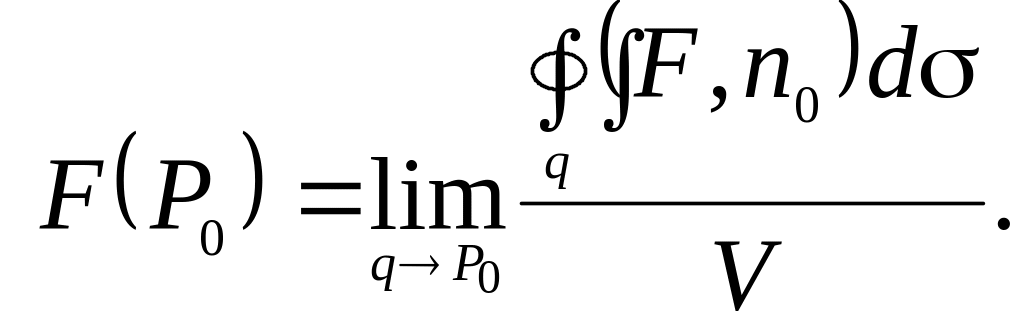
Определение
4. Дивергенция
(или расходимость)
– это скалярная величина, характеризующая
мощность источников или стоков векторного
поля в каждой его точке. Она равна пределу
потока векторного поля через замкнутую
поверхность, отнесенного к объему,
заключенному внутри поверхности, при
стягивании поверхности в точку.
Если
векторное поле в области
задано тремя скалярными функциями –
проекциями вектора поля на координатные
оси
,
то
дивергенцию поля в произвольной точке
находят по формуле
div
(6.3.5)
при
этом предполагается, что функции
,
,
во всех точках области имеют непрерывные
частные производные.
Замечание
1. В формуле
(6.3.5) не пишут индекс
,
так как эта формула справедлива в любой
точке поля.
Замечание
2. Для плоского
поля в правой части формулы (6.3.5)
отсутствует третье слагаемое.
Отметим некоторые
свойства дивергенции.
1.
Если
– постоянный вектор, то div
2.
div
div
+
div
,
где
и
– произвольные постоянные.
3.
Если
– скалярная функция,
– вектор, то
div
div
+
gradU.
Доказательство:
div
gradU+U
div
.
Пример
5. Найти
дивергенцию однородного поля
const.
Решение.
Проекции вектора поля на координатные
оси
const,
const,
const
имеют
вид
div
Однородное поле
не имеет источников.
Пример
6. Найти
дивергенцию радиус-вектора.
Решение.
Координаты радиус-вектора
.
div
Каждая точка поля
радиус-вектора является источником
мощности 3.
Пример
7. Доказать
равенство div
grad
f
div
.
Решение.
Пусть
.
Тогда
и
div
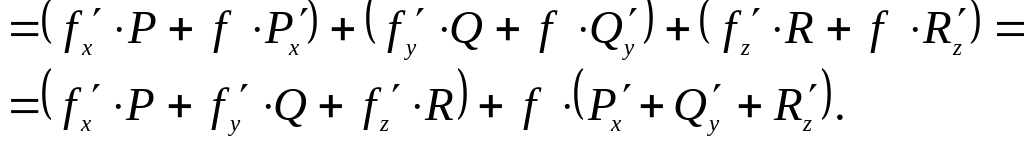
В
первой скобке стоит скалярное произведение
градиента скалярного поля f
на вектор F,
а во второй – дивергенция векторного
поля F.
Таким образом, div
grad
f
div
.
Дивергенция
– это локальная характеристика векторного
поля. Она характеризует свойства поля
в точках и бесконечно малых окрестностях,
прилегающих к этим точкам.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Диверге́нция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.
Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учётом знака. Поэтому можно дать более короткое определение дивергенции:
- дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой (в условиях конкретной задачи) окрестности каждой внутренней точки области определения поля.
Оператор дивергенции, применённый к полю 
или
.
Определение[править | править код]
Определение дивергенции выглядит так:
где 





Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат).
Определение легко и прямо обобщается на любую размерность 


Определение в декартовых координатах[править | править код]
Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением
(здесь F — обозначено некое векторное поле с декартовыми компонентами

Это же выражение можно записать с использованием оператора набла
Многомерная, а также двумерная и одномерная, дивергенция определяется в декартовых координатах в пространствах соответствующей размерности совершенно аналогично (в верхней формуле меняется лишь количество слагаемых, а нижняя остается той же, подразумевая оператор набла подходящей размерности).
Физическая интерпретация[править | править код]
С точки зрения физики (и в строгом смысле, и в смысле интуитивного физического образа математической операции) дивергенция векторного поля является показателем того, в какой степени данная точка пространства (точнее достаточно малая окрестность точки) является источником или стоком этого поля:
— точка поля является источником;
— точка поля является стоком;
— стоков и источников нет, либо они компенсируют друг друга.
Простым, хоть, быть может, и несколько схематическим, примером может служить озеро (для простоты — постоянной единичной глубины со всюду горизонтальной скоростью течения воды, не зависящей от глубины, давая, таким образом, двумерное векторное поле на двумерном пространстве). Если угодно иметь более реалистическую картину, то можно рассмотреть горизонтальную проекцию скорости, проинтегрированную по вертикальной пространственной координате, что даст ту же картину двумерного векторного поля на двумерном пространстве, причём картина качественно будет для наших целей не сильно отличаться от упрощённой первой, количественно же являться её обобщением (весьма реалистическим). В такой модели (и в первом, и во втором варианте) родники, бьющие из дна озера, будут давать положительную дивергенцию поля скоростей течения, а подводные стоки (пещеры, куда вода утекает) — отрицательную дивергенцию.
Дивергенция вектора плотности тока даёт минус скорость накопления заряда в электродинамике (так как заряд сохраняется, то есть не исчезает и не появляется, а может только переместиться через границы какого-то объёма, чтобы накопиться в нём или уйти из него; а если и возникают или исчезают где-то положительные и отрицательные заряды — то только в равных количествах). (См. Уравнение непрерывности).
Дивергенция поля, имеющего силовую природу, как напряженность поля в электростатике, электродинамике или ньютоновской теории гравитации, дивергенция определяет тоже положение источников поля, которые в этом случае называются зарядами (электрическим зарядом в случае электростатики и электродинамики, массой в случае ньютоновской гравитации). В этих теориях дивергенция напряженности поля, с точностью до постоянного множителя[1], равна плотности заряда (в электростатике и электродинамике — плотности электрического заряда, в случае гравитации — плотности массы; кроме того, случай гравитации отличается знаком этой константы).
— для электрического поля и плотности электрического заряда, в СИ,
— для ньютоновского гравитационного поля.
Геометрическая интерпретация[править | править код]
Наверное, наиболее наглядной и простой общей геометрической интерпретацией дивергенции (помимо самого определения, которое тоже достаточно геометрично)
является интерпретация с использованием для изображения векторного поля его интегральных линий (называемых также силовыми линиями в случае полей силовой природы или линиями тока в случае поля скорости течения жидкости или газа). Точки, где появляются новые линии (с направлением от этой точки) являются точками, где дивeргенция поля положительна; где линии кончаются (с направлением линии к точке), там дивергенция отрицательна. Где количество линий постоянно вдоль их хода, то есть где начинается столько же линий, сколько заканчивается, там дивергенция поля нулевая.
- Эта интерпретация основана на соглашении, в соответствии с которым на рассматриваемые линии наложено условие, что густота линий вблизи данной точки пропорциональна величине векторного поля в этой области (при этом умозрительно можно — для того, чтобы описание поля этими линиями было вполне детальным, — считать густоту линий сколь угодно большой, и даже бесконечной, важна только пропорциональность густоты где-то величине вектора поля там же). В противном случае, конечно, по крайней мере в случае непрерывного распределения источников (зарядов), любую интегральную линию поля можно было бы продолжать и представление об их начале или конце где-то было бы мало осмысленным, кроме разве что мест дискретных, а не непрерывно распределенных, источников.
Если в качестве векторного поля (на двумерном пространстве) взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся). Впрочем, это никак не определяет знака или равенства нулю дивергенции такого поля на склонах.[2]
Дивергенция в физике[править | править код]
Дивергенция — одна из наиболее широко употребимых в физике операций. Представляет собой одно из достаточно немногих базовых понятий теоретической физики и является одним из базовых элементов физического языка.
В стандартной формулировке классической теории поля дивергенция занимает центральное место (в альтернативных формулировках может не находиться в самом центре изложения, но всё равно остается важным техническим инструментом и важной идеей).
В электродинамике дивергенция входит в качестве главной конструкции в два из четырёх уравнений Максвелла. Основное уравнение теории ньютоновской гравитации в полевом виде также содержит в качестве основной конструкции дивергенцию (напряженности гравитационного поля). В тензорных теориях гравитации (включая ОТО, и имея в виду в первую очередь её) основное полевое уравнение (в ОТО, но как правило — так или иначе — и в альтернативных современных теориях тоже) также включает в себя дивергенцию в некотором обобщении. То же можно сказать о классической (то есть не квантовой) теории практически любого из фундаментальных полей, как экспериментально известных, так и гипотетических.
Помимо этого, как видно из приведённых выше примеров, дивергенция применима и в чисто геометрическом плане, а также — особенно часто — к различным материальным потокам (дивергенция скорости течения жидкости или газа, дивергенция плотности электрического тока и т.п.).
Свойства[править | править код]
Следующие свойства могут быть получены из обычных правил дифференцирования.
- Линейность: для любых векторных полей F и G и для всех вещественных чисел a и b
- Если φ — скалярное поле, а F — векторное, тогда:
или
- Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:
или
- Дивергенция от градиента есть лапласиан:
- Дивергенция от ротора:
Дивергенция в ортогональных криволинейных координатах[править | править код]
![={frac {1}{H_{1}H_{2}H_{3}}}left[{frac {partial }{partial q_{1}}}(A_{1}H_{2}H_{3})+{frac {partial }{partial q_{2}}}(A_{2}H_{3}H_{1})+{frac {partial }{partial q_{3}}}(A_{3}H_{1}H_{2})right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/641bb9c7caad31dff5828d19960836a9f79de9e0)

Цилиндрические координаты[править | править код]
Коэффициенты Ламе:
Отсюда:
Сферические координаты[править | править код]
Коэффициенты Ламе:
Отсюда:
Параболические координаты[править | править код]
Коэффициенты Ламе:
.
Отсюда:
Эллиптические координаты[править | править код]
Коэффициенты Ламе:
.
Отсюда
Дивергенция в произвольных криволинейных координатах и её обобщение[править | править код]
Формулу для дивергенции векторного поля в произвольных координатах (в любой конечной размерности) нетрудно получить из общего определения через предел отношения потока к объёму, воспользовавшись тензорной записью смешанного произведения и тензорной формулой объёма.
Существует обобщение операции дивергенции на действие не только на векторы, но и на тензоры более высокого ранга.
В общем случае дивергенция определяется ковариантной производной:
, где
— координатные векторы.
Это позволяет находить выражения для дивергенции в произвольных координатах для векторного:
.
или тензорного поля:
.
В общем случае, дивергенция понижает ранг тензора на 1.
Свойства дивергенции тензора[править | править код]
См. также[править | править код]
- Векторный анализ
- Теорема Остроградского — Гаусса
- Формулы векторного анализа
Примечания[править | править код]
- ↑ Для теории в вакууме, являющейся фундаментальной, эта константа — фундаментальная константа, зависящая только от системы единиц измерения; для феноменологической теории в способной поляризоваться среде дело несколько усложняется, поскольку на коэффициент пропорциональности влияют свойства (поляризуемость) среды — однако для однородной среды этот коэффициент также оказывается константой, хотя уже не фундаментальной, а зависящей от вещества среды.
- ↑ Если определить векторное поле такого рода так, что модуль вектора этого поля всегда единичен (только указывая направление), то на простых примерах (скажем, для полностью симметричной горы) нетрудно увидеть, что дивергенция будет положительной, пока не кончается скат (впрочем, при наложении условия единичности вектора направления быстрейшего спуска в точках вершин и ям он будет не определен, а дивергенция в них будет бесконечной по величине); если же не накладывать условия единичности вектора, а взять (как самое простое) минус градиент высоты, то дивергенция будет зависеть от выпуклости или вогнутости склона (в разных его точках), которая вообще говоря может быть на склоне везде разной, как по знаку, так и по величине (в отличие от вершин, которые всегда выпуклы, а ям, всегда вогнутых — если иметь в виду сами точки экстремумов высоты).
Дивергенция (расходимость) — скалярный дифференциальный оператор векторного поля, который показывает, насколько поле имеет тенденцию расходиться из данной точки.
Определение
Оператор дивергенции обозначается так: div F.
Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением
Это же выражение можно записать с использованием оператора набла
Физическая интерпретация
С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или потребителем потока поля. То есть, альтернативное определение дивергенции выглядит:
где Ф — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объем V. Это определение применимо, в отличие от первого, не только к декартовым системам координат



Например, если в качестве векторного поля взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся).
Свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
- Линейность
для любых векторных полей F и G и для всех действительных чисел a и b.
- Если φ — скалярное поле, а F — векторное, тогда:
или
- Свойство, связывающее векторные поля F и G, заданные в трехмерном пространстве, с ротором:
или
- Дивергенция от градиента есть лапласиан:
- Дивергенция от ротора:
Дивергенция в ортогональных криволинейных координатах
,
где Hi — коэффициенты Ламе.
Цилиндрические координаты
Коэффициенты Ламе:
.
Отсюда:
Сферические координаты
Коэффициенты Ламе:
.
Отсюда:
См. также
- Векторный анализ
- Теорема Остроградского — Гаусса
- Ротор
- Градиент
- Оператор набла
- Лапласиан
- Формулы векторного анализа
bg:Дивергенция (математика)
ca:Divergència
cs:Divergence
he:דיברגנץ
hu:Divergencia (vektoranalízis)
nl:Divergentie (vectorveld)
pl:Dywergencja
sk:Divergencia (vektorové pole)
ta:விரிதல் (திசையன் நுண்கணிதம்)
uk:Дивергенція
vi:Toán tử div
Главная
»
Общенаучные дисциплины
»
Математика (2 семестр)
»
Дивергенция и ротор векторного поля. Свойства. Формула Стокса и Остроградского.
Дивергенция и ротор векторного поля. Свойства. Формула Стокса и Остроградского.
Пусть X — заданное многообразие, T — касательное расслоение, то есть отображение, которое каждой точке X сопоставляет касательное пространство в данной точке T | X, тогда сечение касательного расслоения является векторным полем.
Таким образом, векторное поле — это отображение, которое ставит каждой точке многообразия в соответствие вектор из касательного пространства в данной точке.
Частные случаи векторных полей
Векторные поля на прямой
Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле.
Векторные поля на плоскости
Если 
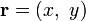
Векторные поля в трёхмерном пространстве
Если 
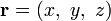
В трёхмерном пространстве имеют смысл следующие характеристики векторного поля
Криволинейный интеграл
где точка означает скалярное произведение, 


Циркуляция — интеграл по замкнутому контуру:
где подынтегральное выражение совпадает с описанным чуть выше, а отличие состоит в пути интегрирования C, который в данном случае по определению замкнут, что обозначается кружком на знаке интеграла.
Поток векторного поля 
,
где Fn — проекция вектора поля на нормаль к поверхности, 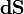
Аналогом производной для векторного поля выступает тензор частных производных (якобиан), который в декартовых координатах имеет вид:
Дивергенция векторного поля — след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:
Это же выражение можно записать с использованием символического оператора набла
Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.
Ротор — векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:
,
где i, j и k — единичные орты для осей x, y и z соответственно.
Для удобства запоминания можно условно представлять ротор как векторное произведение:
Градиент — важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю fвекторное поле называется градиентом f:
или, записывая с помощью наблы:
Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).
Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.
Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.
Интегральные кривые (силовые линии)
Силовые линии магнитного поля
Силовой линией (векторной линией или интегральной кривой, в зависимости от контекста) для поля 
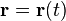
Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.
Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.
Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.
Общая формулировка
Пусть на ориентируемом многообразии M размерности n заданы ориентируемое p-мерное подмногообразие σ и дифференциальная форма ω степени p − 1 класса C1 (
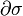
где dω обозначает внешний дифференциал формы ω.
Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия M.
Частные случаи
Формула Ньютона — Лейбница
Пусть дана кривая l, соединяющая две точки a и b (одномерная цепь) в многообразии произвольной размерности. Форма ω нулевой степени класса C1 — это дифференцируемая функция f. Формула Стокса тогда записывается в виде
Теорема Грина
Пусть M — плоскость, а D — некоторая её ограниченная область с кусочно-гладкой жордановой границей. Форма первой степени, записанная в координатах x и y — это выражение 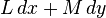
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.



















![operatorname {div}{mathbf {A}}(r,theta ,phi )={frac {1}{r^{2}}}{frac {partial }{partial r}}left[A_{r}r^{2}right]+{frac {1}{rsin {theta }}}{frac {partial }{partial theta }}left[A_{theta }sin {theta }right]+{frac {1}{rsin {theta }}}{frac {partial }{partial phi }}{big [}A_{phi }{big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7548260aacea52496d0207039271424183f6da97)

![operatorname {div}{mathbf {A}}(xi ,eta ,phi )={frac {4}{xi +eta }}{frac {partial }{partial xi }}left[A_{xi }{frac {{sqrt {xi ^{2}+xi eta }}}{2}}right]+{frac {4}{xi +eta }}{frac {partial }{partial eta }}left[A_{eta }{frac {{sqrt {eta ^{2}+xi eta }}}{2}}right]+{frac {1}{{sqrt {xi eta }}}}{frac {partial }{partial phi }}{Big [}A_{phi }{Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8afe2cebf173d4302bcf706c44dba63f0f5c0066)

![operatorname {div}{mathbf {A}}(xi ,eta ,phi )={frac {1}{sigma (xi ^{2}-eta ^{2})}}{frac {partial }{partial xi }}left[A_{xi }{sqrt {(xi ^{2}-eta ^{2})(xi ^{2}-1)}}right]+](https://wikimedia.org/api/rest_v1/media/math/render/svg/f087bcb396ec52f751728abe18591c5cedd3593c)
![{displaystyle +{frac {1}{sigma (xi ^{2}-eta ^{2})}}{frac {partial }{partial eta }}left[A_{eta }{sqrt {(xi ^{2}-eta ^{2})(1-eta ^{2})}}right]+{frac {1}{sigma {sqrt {(xi ^{2}-1)(1-eta ^{2})}}}}{frac {partial }{partial phi }}{Big [}A_{phi }{Big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2621e1b2b3350c258cd69281d78417ccf485fe7)













![{displaystyle operatorname {div} (mathbf {A} )=operatorname {div} (mathbf {q_{1}} A_{1}+mathbf {q_{2}} A_{2}+mathbf {q_{3}} A_{3})={frac {1}{H_{1}H_{2}H_{3}}}left[{frac {partial }{partial q_{1}}}(A_{1}H_{2}H_{3})+{frac {partial }{partial q_{2}}}(A_{2}H_{3}H_{1})+{frac {partial }{partial q_{3}}}(A_{3}H_{1}H_{2})right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbd8e5b7e4881d20ff947833a2f80b047bdc3126)

![{displaystyle operatorname {div} mathbf {A} (r,theta ,z)={frac {1}{r}}left[{frac {partial }{partial r}}(A_{1}r)+{frac {partial }{partial theta }}(A_{2})+{frac {partial }{partial z}}(A_{3}r)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de863daa754668e851c7e9402065fd187e41799c)

![{displaystyle operatorname {div} mathbf {A} (r,theta ,phi )={frac {1}{r^{2}sin {theta }}}left[{frac {partial }{partial r}}(A_{1}r^{2}sin {theta })+{frac {partial }{partial theta }}(A_{2}rsin {theta })+{frac {partial }{partial phi }}(A_{3}r)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8814791afedaffd03f4bc7747f6fe31c6f1879da)
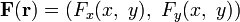
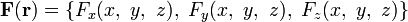
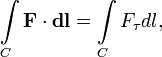
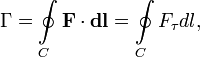
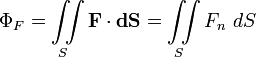 ,
,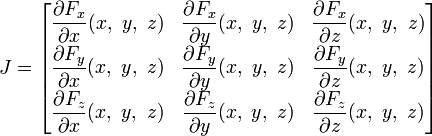
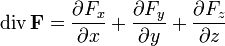
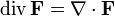
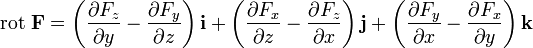 ,
,