Определение формулы касательной к окружности
| Коэффициенты окружности |
| Точка на окружности, через которую надо провести касательную |
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Касательная к окружности
Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то “Касательная к окружности – это прямая пересекающая окружность в двух совпадающих точках”
Окружность на плоскости может быть представлена в виде нескольких исходных данных
1. В виде координат центра окружности (x0,y0) и её радиуса R.
2. В виде общего уравнения
В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на координатах центра окружности и радиусе.
Наша задача, зная параметры окружности и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.
Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка
Итак, если окружность выражена формулой
Уравнение касательной к окружности если нам известны параметры общего уравнения таково:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в заданной точке.
ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.
Примеры
Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой
Касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.

. Угол равен , где — центр окружности. Его сторона касается окружности. Найдите величину меньшей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол — прямой. Из треугольника получим, что угол равен градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги — тоже градуса.
. Найдите угол , если его сторона касается окружности, — центр окружности, а большая дуга окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Это чуть более сложная задача. Центральный угол опирается на дугу , следовательно, он равен градусов. Тогда угол равен . Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол — прямой. Тогда угол равен .
. Хорда стягивает дугу окружности в . Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.

Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол равен градуса, и тогда угол равен градусов, то есть половине угловой величины дуги .
Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
. К окружности, вписанной в треугольник , проведены три касательные. Периметры отсеченных треугольников равны , , . Найдите периметр данного треугольника.

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника складывается из периметров отсеченных треугольников.
Ты нашел то, что искал? Поделись с друзьями!
Вот более сложная задача из вариантов ЕГЭ:
. Около окружности описан многоугольник, площадь которого равна . Его периметр равен . Найдите радиус этой окружности.

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку с вершинами . Получились треугольники и .
Очевидно, что площадь многоугольника .
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?
Касательная к окружности
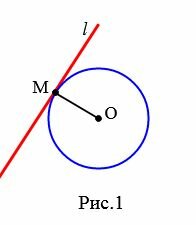
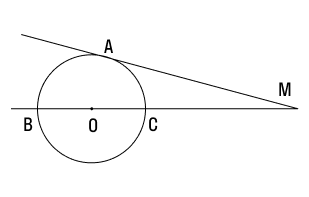
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.
Свойство касательной
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.
Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)
Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.
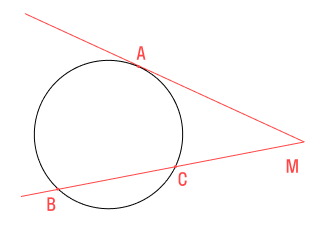
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.
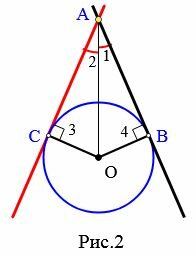
Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.
Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.
Теорема, обратная теореме о свойстве касательной
Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.
Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).
Построение касательной к окружности
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).
Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).
Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/kasatelnaya-k-okruzhnosti-i-svojstva-otrezkov-kasatelnyx/
http://matworld.ru/geometry/kasatelnaya-k-okruzhnosti.php
[/spoiler]
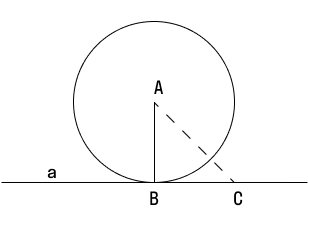
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Решение:
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° – ∠САО – ∠АСО = 180° – 90° – 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно,
АВ = 62°.
Ответ:
АВ = 62°.
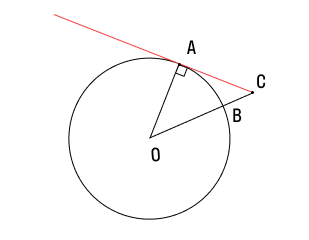
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
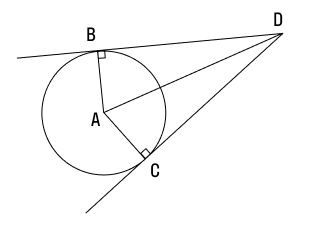
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
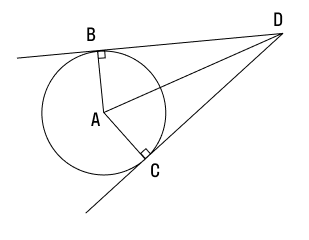
Ответ: ∠BDA = 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° – ∠МКN) : 2 = (180° – 50°) : 2 = 65°
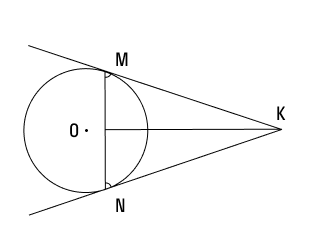
Ответ: ∠NМК = 65°.
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
AB2 = AD × AC
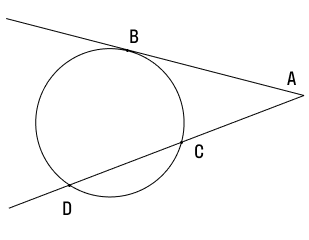
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ – ВС = 16 – 12 = 4 (см)
МА2 = МВ × МС = 16 х 4 = 64
МА = √
64= 8 (см)
Ответ: MA = 8 см.
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА2 = МВ × МС.
Значит:
(у + R)2 : 4 = (у + R) × (у – R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
(у + R) : 4 = (у – R)
у = 5R : 3
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Согласно свойствам угла между касательной и хордой, ∠АВС = ½
АВ.
Ответ:
АВ = 64°.
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
Ответ: ∠ОМК = 6°.
Касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Расскажем подробнее, что такое касательная и секущая.
Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.

Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.
Теорема 1.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке радиус OA перпендикулярен прямой m.
Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Доказательство:

Дана окружность с центром O.
Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и
Проведем радиусы OB и OC в точки касания.
По свойству касательной, и
.
В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и
Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.

Доказательство:
Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.
Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Угол ACМ на рисунке равен половине угловой величины дуги AC.
Доказательство теоремы здесь.
Теорема 5, о секущей и касательной.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.

Доказательство теоремы смотрите здесь.
Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.
Задача 1.
Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение:
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.
Ответ: 62.
Задача 2.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Решение:
Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен
Ответ: 26.
Задача 3.
Хорда AB стягивает дугу окружности в Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:
Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.
Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Задача 4.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Решение:
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.
Ответ: 24.
Вот более сложная задача из вариантов ЕГЭ:
Задача 5.
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Решение:
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.
Очевидно, что площадь многоугольника
Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.

где p — полупериметр многоугольника.
По условию, P = 10, S = 5, тогда
Ответ: 1
Задачи ЕГЭ
1. Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.

Решение:
По условию, CA — касательная, A — точка касания.
. Треугольник ACO — прямоугольный,
.
Угол — центральный, и он равен угловой величине дуги AB, на которую опирается. Значит, градусная мера дуги AB равна
. Это меньшая дуга AB, а большая — с другой стороны от точек A и B, и она больше 180 градусов.
Ответ: 63.
2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна . Найдите угол ACB. Ответ дайте в градусах.

Решение:
Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть
AC и BC — касательные, поэтому , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.
Сумма углов четырехугольника ACBO равна
Ответ: 122.
3. Хорда AB стягивает дугу окружности в . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:
Применим теорему об угле между касательной и хордой.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Значит, угол ABC равен .
Ответ: 46.
4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен . Найдите угол AOB. Ответ дайте в градусах.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
Поэтому меньшая дуга AB окружности равна . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен
.
Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.
Ответ: 64.
5. Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:
Ответ: 118.
6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Решение:
По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна . На эту дугу опирается центральный угол AOB, он равен
. Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.
Ответ: 26.
Задачи ОГЭ по теме: Касательная к окружности
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Решение:
Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:
Ответ: 5.
2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный . Найдите величину угла OMK. Ответ дайте в градусах.

Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой. Тогда Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому
Ответ: 7.
3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Решение:
Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:
Ответ: 10.
4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Решение:
Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:
Ответ: 40.
5. Касательные в точках A и B к окружности с центром O пересекаются под углом . Найдите угол ABO. Ответ дайте в градусах.
Решение:

Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна . Угол AOB — центральный, он равен дуге, на которую опирается, то есть
. Треугольник AOB равнобедренный,
Ответ: 36.
6. Из точки A проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки A до точки O равно 8.
Решение:

Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.
OB — OC как радиусы окружности, гипотенуза общая. Значит,
Из треугольника AOB найдём OB, то есть радиус окружности.
Ответ: 4.
7. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.

Решение:
По теореме о секущей и касательной,
Ответ: 4.
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Решение:
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
Ответ: 36.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Касательная к окружности» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Что такое касательная к окружности
8 июля 2018
- Домашняя работа
- Ответы и решения
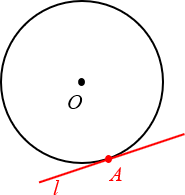
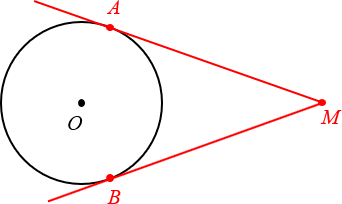
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
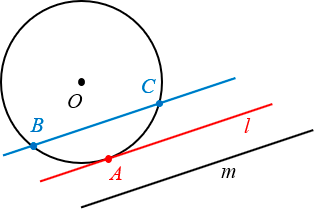
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.
Основные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
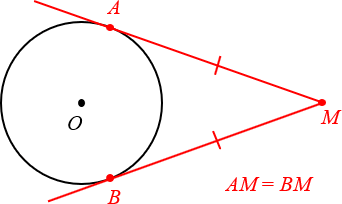
2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
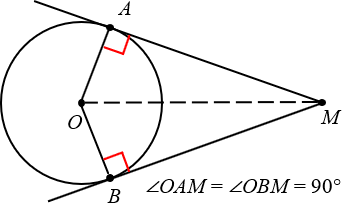
Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
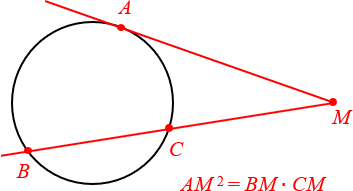
3. Соотношение между касательной и секущей
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной
4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
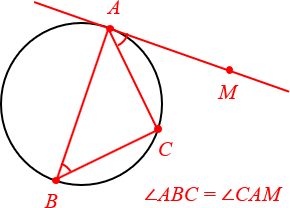
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.

Смотрите также:
- Вписанный угол в геометрии

- Задачи B12, сводящиеся к линейным уравнениям

- Геометрическая вероятность

- Задача 18: метод симметричных корней

- Задача B2 про комиссию в терминале

- Значение тригонометрических функций


График функции (чёрная кривая) и касательная прямая (красная прямая)
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Строгое определение[править | править код]
Замечание[править | править код]
Прямо из определения следует, что график касательной прямой проходит через точку 

где 

Производная в точке 

Касательная как предельное положение секущей[править | править код]
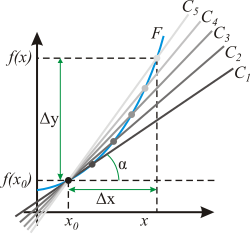
Пусть 



Эта прямая проходит через точку 


В силу существования производной функции 


а в силу непрерывности арктангенса и предельный угол
Прямая, проходящая через точку 

Касательная к окружности[править | править код]

Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
Свойства[править | править код]
- Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с лучом, проведённым из центра окружности, является тангенсом угла между этим лучом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».
Вариации и обобщения[править | править код]
Односторонние полукасательные[править | править код]
См. также[править | править код]
- Дифференцируемая функция
- Касательное пространство
- Нормаль, бинормаль
- Теорема о секущих
Литература[править | править код]
- Топоногов В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
- Касательная // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.










