Как найти длину акружности

Как найти длину акружности

8 способов найти длину окружности

Выбирайте формулу, ориентируясь на известные величины.

8 способов найти длину окружности

1. Как найти длину окружности через диаметр

Просто умножьте диаметр на число пи.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • d —диаметр окружности.

2. Как найти длину окружности через радиус

Умножьте число пи на два радиуса.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • r — радиус окружности.

3. Как вычислить длину окружности через площадь круга

Умножьте число пи на четыре площади круга.

Найдите корень из результата.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
  • π (пи) — константа, равная 3,14.

4. Как найти длину окружности через диагональ вписанного прямоугольника

Умножьте число пи на диагональ.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • d – любая диагональ прямоугольника.

5. Как вычислить длину окружности через сторону описанного квадрата

Умножьте число пи на сторону квадрата.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • a – любая сторона квадрата.

6. Как найти длину окружности через стороны и площадь вписанного треугольника

Перемножьте стороны треугольника.

Поделите результат на площадь и на два.

Умножьте полученное число на пи.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • S – площадь треугольника.
  • a, b, c – стороны треугольника.

7. Как найти длину окружности через площадь и полупериметр описанного треугольника

Поделите площадь треугольника на его полупериметр.

Умножьте результат на число пи и на два.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • π (пи) — константа, равная 3,14.
  • S – площадь треугольника.
  • p – полупериметр треугольника (равен половине от суммы всех сторон).

8. Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.

Найдите синус полученного числа.

Разделите сторону многоугольника на результат.

Умножьте получившееся число на пи.

Иллюстрация: Лайфхакер
  • O — искомая длина окружности.
  • a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
  • π (пи) — константа, равная 3,14.
  • N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✏️🎓

  • Как найти периметр прямоугольника
  • 8 способов найти периметр треугольника
  • 7 способов найти площадь прямоугольника
  • Как перевести обычную дробь в десятичную
  • Как освоить устный счёт школьникам и взрослым
Источник

Как посчитать длину окружности

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как посчитать длину окружности

Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

окружность Для того чтобы определить длину окружности вам необходимо знать её радиус или диаметр, либо её площадь. Зная хотя бы один из этих параметров, введите его в соответствующие поле и получите результат в виде длины окружности (длины дуги в 360 градусов).

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

её диаметр ?

Ответ:

0

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d, где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

её радиус ?

Ответ:

0

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r, где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

её площадь ?

Ответ:

0

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅√S/π, где π ≈ 3.14

Пример

Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.

См. также

Источник

Оглавление:

  • 📝 Как это работает?
  • 🤔 Частые вопросы и ответы
  • 📋 Похожие материалы
  • 📢 Поделиться и комментировать

Что такое окружность?

Что такое окружность

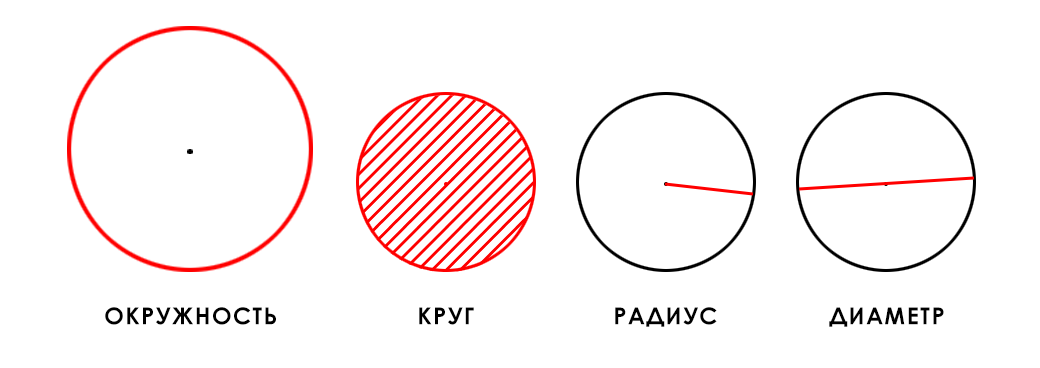
Окружность – это замкнутая плоская кривая, ограничивающая круг.

Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.

Как найти длину окружности?

Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.

По диаметру

Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.

Формула будет такой:

L = π × d

Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.

Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:

L = 3,14 × 100 = 314 мм.

Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.

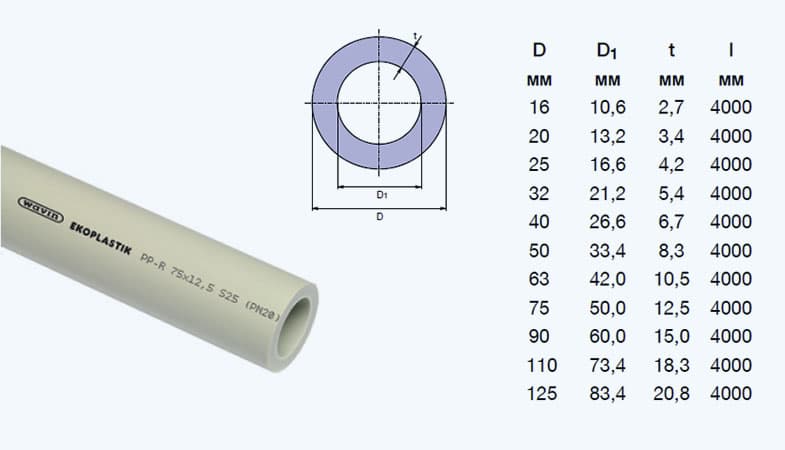
Рассчитать длину окружности трубы

Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.

Зная радиус

Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.

Формула расчёта выглядит следующим образом:

L = 2π × R

Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.

К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:

L = 2 × 3,14 × 26 = 163,28 мм.

Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.

Через площадь круга

И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:

L = (4Sπ)1/2

Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.

То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.

Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.

Круга на полях: площадь и периметр

Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:

  1. Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
  2. И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.

Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.

❓Вопросы и ответы

И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.

Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?

Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:

  • Площадь круга
  • Длина окружности
  • Диаметр
  • Радиус

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?

Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.

Что такое внутренняя и внешняя окружность? Чем они отличаются?

Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

  • Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
  • Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
  • Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
  • Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
  • Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
  • Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
  • Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
  • Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
  • Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
  • Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Показать комментарии

Источник


Загрузить PDF


Загрузить PDF

Окружность – это плоская замкнутая кривая, все точки которой равноудалены от центральной точки.[1]
 Длина окружности (С) – это длина замкнутой кривой, которая и образует окружность.[2]
 Площадь круга (А) – это величина пространства, которое ограничено окружностью.[3]
 Площадь круга и длина окружности вычисляются по формулам, в которых присутствует радиус (или диаметр) окружности и число «пи».

  1. Изображение с названием Find the Circumference and Area of a Circle Step 1

    1

    Формула для вычисления длины окружности. Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14)[4]
    , r – радиус окружности, d – диаметр окружности.[5]

    • Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
    • Длина окружности измеряется в любых единицах измерения длины: в метрах, сантиметрах, миллиметрах и так далее.

  2. Изображение с названием Find the Circumference and Area of a Circle Step 2

    2

    Величины формулы. В формулу для нахождения длины окружности входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.

    • Радиус окружности (r) – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
    • Диаметр окружности (d) – это отрезок, проходящий через центр окружности и соединяющий любые две точки, лежащие на окружности.[6]
    • Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[7]
       В большинстве математических вычислений число «пи» округляется до 3,14.

  3. Изображение с названием Find the Circumference and Area of a Circle Step 3

    3

    Измерьте радиус или диаметр окружности. Совместите начало линейки с любой точкой на окружности и сделайте так, чтобы линейка соприкасалась с центром окружности. Измерьте расстояние от точки до центра окружности, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.

    • В большинстве математических задач радиус или диаметр будет дан.

  4. Изображение с названием Find the Circumference and Area of a Circle Step 4

    4

    Подставьте значения величин в формулу. Найдя радиус и/или диаметр окружности, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой C = 2πr, а если диаметр, формулой C = πd.

    • Пример: найдите длину окружности, радиус которой равен 3 см.
      • Напишите формулу: C = 2πr
      • Подставьте данное значение в формулу: C = 2π3
      • Перемножьте: C = (2*3*π) = 6π = 18,84 см
    • Пример: найдите длину окружности, диаметр которой равен 9 м.
      • Напишите формулу: C = πd
      • Подставьте данное значение в формулу: C = 9π
      • Перемножьте: C = (9*π) = 28,26 м

  5. Изображение с названием Find the Circumference and Area of a Circle Step 5

    5

    Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.

    • Найдите длину окружности с диаметром 5 м.
      • C = πd = 5π = 15,7 м
    • Найдите длину окружности с радиусом 10 м.
      • C = 2πr = C = 2π10 = 2*10* π = 62,8 м

    Реклама

  1. Изображение с названием Find the Circumference and Area of a Circle Step 6

    1

    Формула для вычисления площади круга. Площадь круга можно вычислить по двум формулам, включающим диаметр или радиус: A = πr2 или A = π(d/2)2[8]
    , где π – число «пи» (математическая константа, приблизительно равная 3,14)[9]
    , r – радиус круга, d – диаметр круга.

    • Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
    • Площадь круга измеряется в любых единицах измерения длины, возведенных в квадрат: в квадратных метрах (м2), в квадратных сантиметрах (см2), в квадратных миллиметрах (мм2) и так далее.

  2. Изображение с названием Find the Circumference and Area of a Circle Step 7

    2

    Величины формулы. В формулу для нахождения площади круга входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.

    • Радиус круга (r) – это отрезок, соединяющий центр круга с любой точкой, лежащей на окружности, которая ограничивает этот круг.
    • Диаметр круга (d) – это отрезок, проходящий через центр круга и соединяющий любые две точки, лежащие на окружности, которая ограничивает этот круг.[10]
    • Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[11]
       В большинстве математических вычислений число «пи» округляется до 3,14.

  3. Изображение с названием Find the Circumference and Area of a Circle Step 8

    3

    Измерьте радиус или диаметр круга. Совместите начало линейки с любой точкой на окружности, ограничивающей круг, и сделайте так, чтобы линейка соприкасалась с центром круга. Измерьте расстояние от точки до центра круга, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.

    • В большинстве математических задач радиус или диаметр будет дан.

  4. Изображение с названием Find the Circumference and Area of a Circle Step 9

    4

    Подставьте значения величин в формулу. Найдя радиус и/или диаметр круга, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой A = πr2, а если диаметр, формулой A = π(d/2)2.

    • Пример: найдите площадь круга с радиусом 3 м.
      • Напишите формулу: A = πr2
      • Подставьте данное значение: A = π32
      • Возведите радиус в квадрат: r2 = 32 = 9
      • Умножьте на число «пи»: A = 9π = 28,26 м2
    • Пример: найдите площадь круга с диаметром 4 м.
      • Напишите формулу: A = π(d/2)2
      • Подставьте данное значение: A = π(4/2)2
      • Разделите диаметр на 2: d/2 = 4/2 = 2
      • Результат возведите в квадрат: 22 = 4
      • Умножьте на число «пи»: A = 4π = 12,56 м2

  5. Изображение с названием Find the Circumference and Area of a Circle Step 10

    5

    Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.

    • Найдите площадь круга с диаметром 7 м.
      • A = π(d/2)2 = π(7/2)2 = π(3,5)2 = 12,25 * π= 38,47 м2.
    • Найти площадь круга с радиусом 3 м.
      • A = πr2 = π32 = 9 * π = 28,26 м2

    Реклама

  1. Изображение с названием Find the Circumference and Area of a Circle Step 11

    1

    Найдите радиус или диаметр окружности. В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.

    • Пример: вычислите длину окружности с радиусом (х + 1).

  2. Изображение с названием Find the Circumference and Area of a Circle Step 12

    2

    Напишите формулу с данным значением. Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.

    • Пример: вычислите длину окружности с радиусом (х + 1).
    • Напишите формулу: C = 2πr
    • Подставьте данное значение: C = 2π(х + 1)

  3. Изображение с названием Find the Circumference and Area of a Circle Step 13

    3

    Вычислите длину окружности так, как если бы переменная была представлена числом. На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.

    • Пример: вычислите длину окружности с радиусом (х + 1).
    • C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
    • Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.

  4. Изображение с названием Find the Circumference and Area of a Circle Step 14

    4

    Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.

    • Найдите площадь круга с радиусом 2х.
      • A = πr2 = π(2x)2 = π4x2 = 12,56x2
    • Найдите площадь круга с диаметром (х + 2).
      • A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π

    Реклама

Об этой статье

Эту страницу просматривали 212 706 раз.

Была ли эта статья полезной?

Источник

Сегодня мы говорим про окружность и круг, друзья мои. У многих шестиклассников, да и не только у них, возникают трудности с этой темой. А она-то как раз и есть ваш реальный шанс на получение хорошей отметки. Да, есть там одна заковырка. Вот она не нравится ребятам. Но я сейчас подробно всё расскажу. Давайте приступим)))

Длина окружности и площадь круга. Можете не понимать. Надо знать 3 формулы и 2 определения

Сначала дам несколько определений. Они очень лёгкие, просто посмотрите:

Есть окружность, а есть круг:

Длина окружности и площадь круга. Можете не понимать. Надо знать 3 формулы и 2 определения

Определения, ребята, есть у вас в учебнике. Их надо знать наизусть, учителя это любят. Выучите их, пожалуйста. А я вам простыми словами расскажу, чтобы совсем понятно было.

  • Окружность – это линия на бумаге или ещё где-нибудь. На асфальте мелом, например.
  • Круг – это часть листа (плоскости).

Как отличить круг от окружности?

Круг я могу вырезать ножницами и у меня в руках будет круглый кусок бумаги. А линию я вам как вырежу?!

Окружность нельзя вырезать ножницами! Она же линия!

Дальше. У вас будут две формулы. Я знаю, что их три, на самом деле – две. Расскажу попозже. Сначала основные определения простыми словами дам:

Ребята! Это радиус! Он соединяет центр окружности (точку О) и любую точку на окружности.
Ребята! Это радиус! Он соединяет центр окружности (точку О) и любую точку на окружности.

А это диаметр. Присмотритесь: вам ничего не показалось?)))

АВ - это диаметр.
АВ – это диаметр.

Вы молодцы, если вам показалось, что один диаметр – это ДВА РАДИУСА! Так и есть!

Значит, вот эти две формулы одинаковые.

d - диаметр, r - радиус
d – диаметр, r – радиус

Запомните: один диаметр – это два радиуса! Один радиус – это половина диаметра! Если знаете диаметр – радиус тоже знаете!!! И наоборот!

Что такое C в этой формуле? Это длина окружности. Если я возьму окружность, мысленно её разрежу и разогну, то получится прямая. Тогда я смогу померить её длину. А можно и не разрезать. Возьмите сантиметровую ленту у бабушки или у мамы. Потом найдите чашку на кухне, отметьте точку (незаметно, чтобы потом смыть) и действуйте по схеме:

Так можно узнать длину окружности в домашних условиях)))
Так можно узнать длину окружности в домашних условиях)))

Есть ещё формула площади круга:

Число "ПИ" - это постоянная величина. Её надо просто запомнить наизусть: 3,14.
Число “ПИ” – это постоянная величина. Её надо просто запомнить наизусть: 3,14.

Тоже легко. В статье я уже не буду об этом писать. А вот видео, в нём я задачи разбираю для шестиклассников, именно на эту тему. Там про площадь круга рассказываю подробно. Для других классов тоже подойдёт, кто не понял, забыл или не успел)))

Подведём итог. Если вы будете знать наизусть определение диаметра и радиуса, если вы будете знать 2 формулы (а на самом деле одну!) длины окружности и одну формулу площади круга, то по этой теме у вас точно будет не ниже четвёрки, друзья мои школьники.

Если статья показалась вам полезной, поставьте, пожалуйста, оценку. Она поможет мне дальше помогать вам)))

Вот здесь кое-что про борьбу со списыванием с сайта ГДЗ

А вот здесь – как учить стихи

P. S.: Про число “ПИ” я ничего не говорила в этой статье. Но в видео я про него рассказываю. Это фантастическое, просто удивительное число!!!!! Но мне места не хватило, В другой раз…

Источник

Добавить комментарий