На сегодняшний день существует несколько способов нахождения апофемы. Каждый из них стоит выбирать в
зависимости от имеющихся в задаче данных.
- Апофема правильной треугольной пирамиды через высоту и
ребро основания - Апофема правильной треугольной пирамиды через площадь
боковых поверхностей и ребро нижнего основания - Апофема правильной треугольной пирамиды через площадь
боковых поверхностей и периметр нижнего основания
Через высоту и ребро основания
Первый способ включает в себя нахождение неизвестной через высоту пирамиды H и ребро основания a. Это
возможно по следующей формуле:
L = √(H² + (a / 2 tan60º)²)
где h — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Кроме того стоит знать тригонометрические функции и их значения при различных углах. В данном случае
тангенс 60º, который равен √3.
Пример. В задаче дана пирамида, у которой имеются два известных значения: высота
равна 3, а сторона основания – 8. Требуется найти апофему правильной треугольной пирамиды. Тогда
результат: b = √(3² + (8 / 2 tan60º)²)= √(9 + (4 / √3)²) = √(9 + (16 / 3)) = √(43/3) = 3.8
Через площадь боковых поверхностей и ребро нижнего основания
Второй вариант для нахождения вышеупомянутой неизвестной основан на площадях боковых поверхностей,
которые являются треугольниками, и ребре основания a. Сначала стоит разобраться с площадью боковых
поверхностей. Она состоит из суммы трех отдельных площадей боковых граней. Площадь прямоугольного
треугольника: S = 0,5 * a * b, где а и b – это катеты прямоугольного
треугольника. Площадь равностороннего треугольника: S = (a * a√3) / 4, где
а – это ребро треугольника. Площадь произвольного треугольника: S = ah / 2, S = (a * b * sinα) / 2.
Формула для нахождения апофемы правильной пирамиды через площадь боковых граней и ребро основания:
L = Sбок / 3/2a
где Sбок — площадь боковых поверхностей, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь
боковых поверхностей равна 120, а ребро основания — 4. Решение: L = 120 / 3/2 * 4 = 20.
Через площадь боковых поверхностей и периметр нижнего основания
Есть еще и третий способ, который основан на площади боковых поверхностей и периметре основания.
Периметр основания — это сумма длин всех сторон, который принадлежат основанию. В правильном
треугольнике длину одного ребра умножают на три. Формула:
L = Sбок / 1/2P
где Sбок — площадь боковых поверхностей, P — периметр основания.
Цифр после
запятой:
Результат в:
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь
боковых поверхностей равна 120, а периметр — 12. Решение: апофема равна L = 120 / 1/2 * 12 = 120 * 6 = 20.
Пирамида представляет собой объемную геометрическую фигуру, многогранник, в основании которого лежит
n-угольник, а остальные n граней- треугольники с общей вершиной, называющейся вершиной пирамиды.
Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а боковые
ребра равны. У треугольной пирамиды за основание принимают треугольник.
Апофемой принято называть высоту боковой грани. Это перпендикуляр, который был опущен из вершины
грани на противолежащую сторону. Часто ее обозначают латинской буквой L или же h, но обязательно
маленькой, потому что большая – это высота не грани, а самой пирамиды. Все апофемы правильной
треугольной пирамиды будут равны между собой. Апофема правильной треугольной пирамиды равна
отношению площади боковых поверхностей на половину периметра нижнего основания.
Ученик
(117),
закрыт
7 лет назад
Pyurbyaha
Мудрец
(11534)
11 лет назад

Дано: KABC – правильная треугольная пирамида
AB=BC=AC=6
KH=10
KD – апофема
Найти: KD, S(BKC), Sпов.
Решение:
HD=√3*BC/6=√3*6/6=√3
KD²=HD²+KH²=√3²+10²=3+100=103 => KD=√103
S(BKC)=BC*KD/2=6*√103/2=3√103
Sбок. =3*S(BKC)=3*3√103=9√103
Sосн. =BC*AD/2=6*3√3/2=9√3
Sпов. =Sбок. +Sосн. =9√103+9√3=9(√103+√3)
Надея Малашевич
Знаток
(375)
11 лет назад
Рассмотрим прямоугольный треугольник, в котором высота – катет, радиус вписанной окружности (6*корень3/6) – катет, апофема – гипотенуза. Апофема равна корень (10^2 + (6*корень3/6)^2) = корень103. Площадь боковой поверхности равна 3 * 6 * корень103 = 18* корень103.
Апофема правильной треугольной пирамиды: формула и пример задачи
При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.
Какая фигура будет рассмотрена?
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.

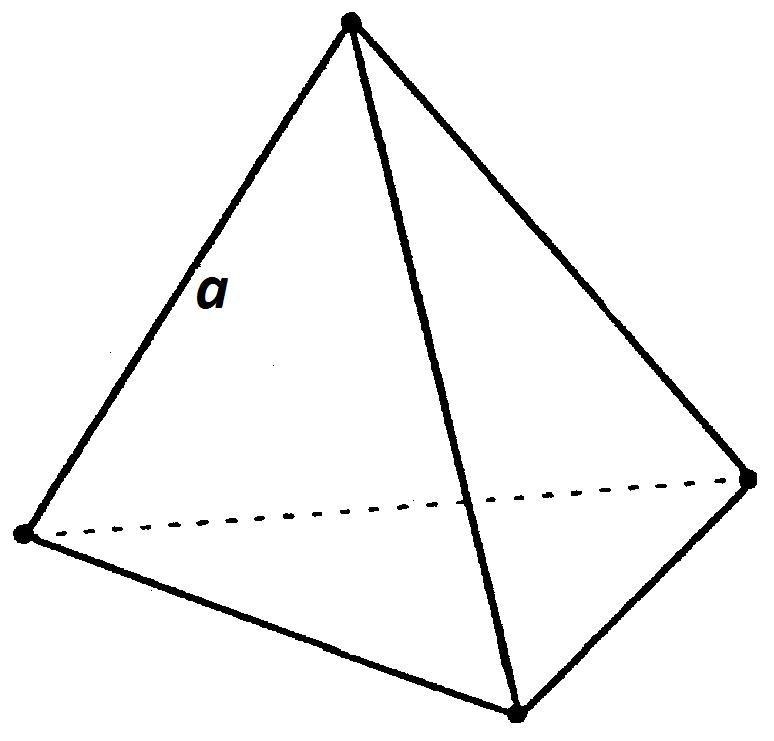
Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.
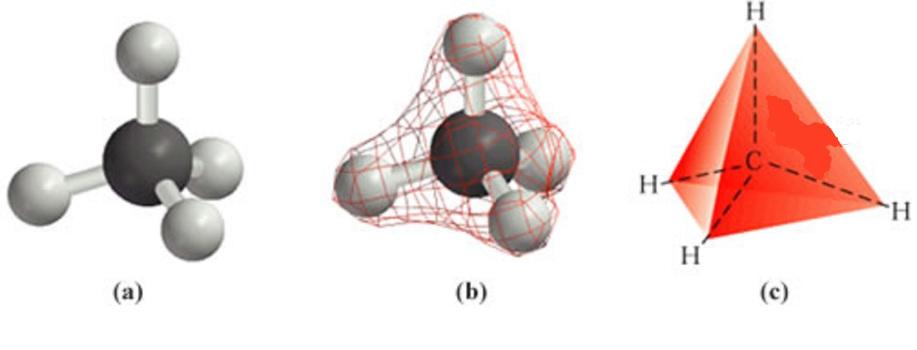
Треугольная пирамида имеет собственное название – тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример – это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.
Формула апофемы пирамиды правильной треугольной
Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.
Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:
- апофемой hb (гипотенуза);
- высотой h (один катет);
- 1/3 медианы m равностороннего треугольника (второй катет).
Длина медианы m треугольника в основании равна:
m = √3/2*a
Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:
hb = √((1/3*m)2 + h2) =>
hb = √(a2/12 + h2)
Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.
Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.
Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:
h = √(a2 – 4/9*m2) = √(a2 – 4/9*3/4*a2) = a*√(2/3)
Теперь применяем формулу для апофемы, получаем:
hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a
Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.
Автор:
15-12-2018 00:52
Жду ваши вопросы и мнения в комментариях
При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.
Какая фигура будет рассмотрена?
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.
Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.
Пирамида является совершенной геометрической фигурой, форму которой можно встретить в некоторых…
Треугольная пирамида имеет собственное название – тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример – это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.
Формула апофемы пирамиды правильной треугольной
Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.
Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:
- апофемой hb (гипотенуза);
- высотой h (один катет);
- 1/3 медианы m равностороннего треугольника (второй катет).
Длина медианы m треугольника в основании равна:
m = √3/2*a
Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:
hb = √((1/3*m)2 + h2) =>
hb = √(a2/12 + h2)
Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.
Решение задачи на определение значения hb
Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.
Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:
h = √(a2 – 4/9*m2) = √(a2 – 4/9*3/ a2) = a*√(2/3)
Теперь применяем формулу для апофемы, получаем:
hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a
Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.
Как найти апофему
Апофемой в пирамиде называют отрезок, проведенный из ее вершины к основанию одной из боковых граней, если отрезок перпендикулярен этому основанию. Боковая грань такой объемной фигуры всегда имеет треугольную форму. Поэтому при необходимости вычисления длины апофемы допустимо использование свойств как многогранника (пирамиды), так и многоугольника (треугольника).

Вам понадобится
- – геометрические параметры пирамиды.
Инструкция
В треугольнике боковой грани апофема (f) является высотой, поэтому при известной длине бокового ребра (b) и угле (γ) между ним и ребром, на которое опущена апофема, можно использовать известную формулу вычисления высоты треугольника. Умножьте заданную длину ребра на синус известного угла: f = b*sin(γ). Эта формула применима к пирамидам любой (правильной или неправильной) формы.
Для вычисления каждой из трех апофем (f) правильной треугольной пирамиды достаточно знать всего один параметр – длину ребра (a). Это объясняется тем, что грани такой пирамиды имеют форму равносторонних треугольников одинаковых размеров. Для нахождения высот каждого из них вычислите половину произведения длины ребра на квадратный корень из трех: f = a*√3/2.
Если известна площадь (s) боковой грани пирамиды, в дополнение к ней достаточно знать длину (a) общего ребра этой грани с основанием объемной фигуры. В этом случае длину апофемы (f) находите удвоением соотношения между площадью и длиной ребра: f = 2*s/a.
Зная общую площадь поверхности пирамиды (S) и периметр ее основания (p) тоже можно вычислить апофему (f), но только для многогранника правильной формы. Удвойте площадь поверхности и разделите результат на периметр: f = 2*S/p. Форма основания в этом случае не имеет значения.
Количество вершин или сторон основания (n) нужно знать в том случае, если в условиях даны длина ребра (b) боковой грани и величина угла (α), который образуют два смежных боковых ребра правильной пирамиды. При таких исходных условиях вычисляйте апофему (f) умножением числа сторон основания на синус известного угла и возведенную в квадрат длину бокового ребра с последующим делением полученной величины пополам: f = n*sin(α)*b²/2.
В правильной пирамиде с четырехугольным основанием для нахождения длины апофемы (f) можно использовать высоту многогранника (H) и длину ребра основания (a). Извлеките квадратный корень из суммы возведенной в квадрат высоты и четверти от возведенной в квадрат длины ребра: f = √(H²+a²/4).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.




