/
/
/ Длина ребра пирамиды
Длина ребра пирамиды
Установить Длина ребра пирамиды на мобильный
Найти боковое ребро правильной пирамиды
зная длину стороны основания и высоту
|
||
|
Сторона основания пирамиды a |
||
|
Число сторон основания пирамиды n |
||
| Высота пирамиды h | ||
|
|
||
| Длина бокового ребра b |
Скачать калькулятор
Рейтинг: 2.7 (Голосов 6)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного треугольника | Сторона квадрата |
| Стороны прямоугольника | Стороны ромба | Боковое ребро параллелепипеда |
олег
983 дн. назад
а если стороны основания разные?
- reply
Михаил
600 дн. назад
Значит пирамида не правильная.
- reply
Добавить комментарий:
Я не робот
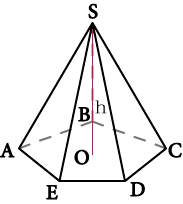
Боковое ребро правильной пирамиды, формула
 |
Боковое ребро правильной пирамиды находится по формуле [ b = sqrt{ h^2 + Big( frac{a}{2sin(frac{180°}{n})} Big) ^2 } ] |
b — Боковое ребро правильной пирамиды (SA или SB или SC или SD или SE)
n — число сторон правильного многоугольника – основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) – основания правильной пирамиды
h — высота правильной пирамиды (OS)
Боковое ребро правильной пирамиды выводится из следующих формул
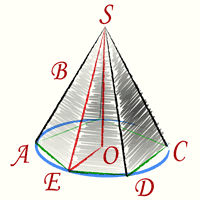
Синим цветом на рисунке изображена описанная вокруг основания правильной пирамиды окружность. Треугольник SOE прямоугольный.
Его стороны: OS — высота правильной пирамиды (h), OE —
радиус описанной окружности вокруг правильного многоугольника (основание правильной пирамиды (R)),
SE — Боковое ребро правильной пирамиды (b).
По теореме Пифагора
[ SE = b = sqrt{ h^2 + R^2 } ]
подставив сюда только радиус описанной окружности получается формула (1).
Вычислить, найти боковое ребро правильной пирамиды по формуле(1)
Боковое ребро правильной пирамиды |
стр. 277 |
|---|
Пирамида – это объемная многогранная геометрическая фигура, состоящая из основания и треугольных
граней, собирающихся в одной точке. У нее есть: вершина, ребра (боковые и основные), боковые грани,
основание, высота и апофема – прямая, соединяющая вершину с границей вписанной в основание
окружности. Правильная пирамида –та, у которой все боковые ребра равны и находятся под одним углом к
основанию, а вершина проецируется на центр окружности, описанной вокруг основания. Тетраэдр –
частный случай правильной пирамиды, в которой боковые ребра равны основным и между собой.
Боковые ребра правильной пирамиды – выходящие из ее вершины, общие для боковых граней стороны. Длина
бокового ребра обозначается латинской буквой «b». Это одно из базовых значений, через которое можно
найти остальные элементы пирамиды. Во многих математических задачах требуется вычислить его или
подставить в формулы.
- Боковое ребро правильной треугольной пирамиды через высоту
и ребро основания - Боковое ребро правильной треугольной пирамиды через высоту
и радиус описанной окружности вокруг правильной треугольной пирамиды - Ребро основания правильной треугольной пирамиды через обьём
и высоту
Ребро основания правильной треугольной пирамиды через объём и высоту
Та часть пространства, которую занимает правильная треугольная пирамида называется ее объемом.
Является физической величиной. Его можно найти через, например, через высоту и сторону основания.
Если нам известен объем и высота правильной треугольной пирамиды, то не составит особого труда найти
ребро основания. Для этого используется формула:
a = √((V * 4 * √3) / H)
где V — объём, H — высота.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретную задачу. Необходимо найти ребро основания, зная что
высота H равна 56 см, a объем 268 см³, подставив все в формулу получим следующий результат: a = √((V * 4 * √3) / H) = √((268 * 4 * √3) / 56) = 5,76 см. Боковое
ребро (b) = 5,76 см.
Боковое ребро правильной треугольной пирамиды через высоту и ребро основания
Боковое ребро правильной пирамиды можно найти по теореме Пифагора, поскольку высота, опущенная в
основание пирамиды, опускается в центр вписанной и описанной окружности для данного многоугольника.
Таким образом формула для нахождения бокового ребра правильной треугольной пирамиды через высоту и
ребро основания будет следующей:
b = √(H² + (a / 2 sin (60º)²))
где H — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 44 мм, a ребро основания
a равно 63 мм, подставив все в формулу получим следующий результат: b = √(H² + (a / 2 sin (60º)²)) = √(44² + (63 / 2 sin (60º)²)) = 57,09 мм.
Боковое ребро (b) = 57.08765 мм.
Боковое ребро правильной треугольной пирамиды через высоту и радиус описанной окружности вокруг
правильной треугольной пирамиды
Если пирамида вписана в окружность, то ее называют описанной вокруг пирамиды. Около пирамиды можно
описать сферу тогда и только тогда, когда около основания пирамиды можно описать
окружность. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее
основания, является центром описанной около основания окружности. Если нам известна высота и радиус
этой описанной окружности, то мы сможем найти боковое ребро. Формула подходит только для правильной
треугольной пирамиды:
b = √(H² + R²)
где H — высота правильной треугольной пирамиды, R — радиус описанной вокруг
окружности.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 73 мм, a радиус описанной
вокруг окружности 114 мм, подставив все в формулу получим следующий результат: b = √(H² + R²) = √(73² + 114²) = 135 мм. Боковое
ребро (b) = 135 мм.
Почти все формулы пирамиды основываются на теореме Пифагора. Таким образом, можно вывести боковое
ребро правильной треугольной пирамиды через высоту и радиус описанной окружности, опираясь на
прямоугольный треугольник, гипотенуза которого является искомой величиной. По одному из основных
свойств правильной пирамиды, ее высота соединяет вершину с центрами окружностей, вписанных и
описанных вокруг пирамиды. Так внутри формируются 2 треугольника с углом 90°. Один состоит из
высоты, бокового ребра и соединяет их с радиусом описанной окружности, другой составляет высота и
апофема, соединённые с радиусом вписанной окружности.
Содержание статьи:
- Пирамида как фигура геометрии
- Элементы пирамиды
- Правильные пирамиды
- Треугольная пирамида
- Четырехугольная пирамида
- Задача на определение бокового ребра пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр – боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.

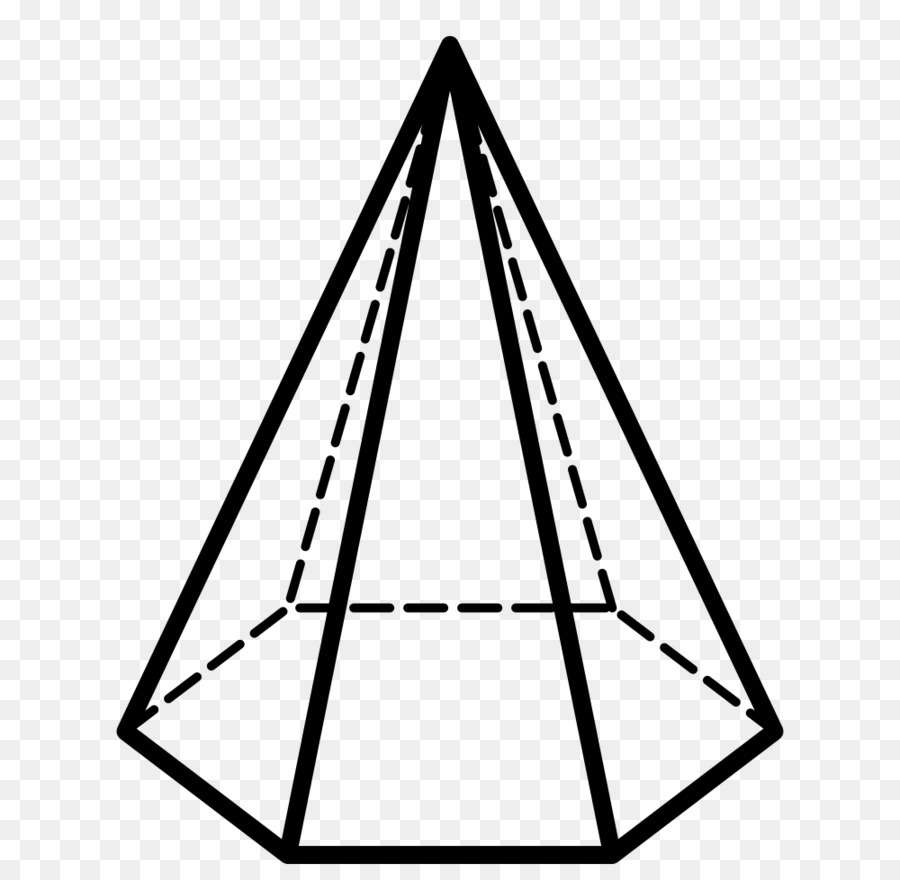
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
- гранями;
- ребрами;
- вершинами.
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника – с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
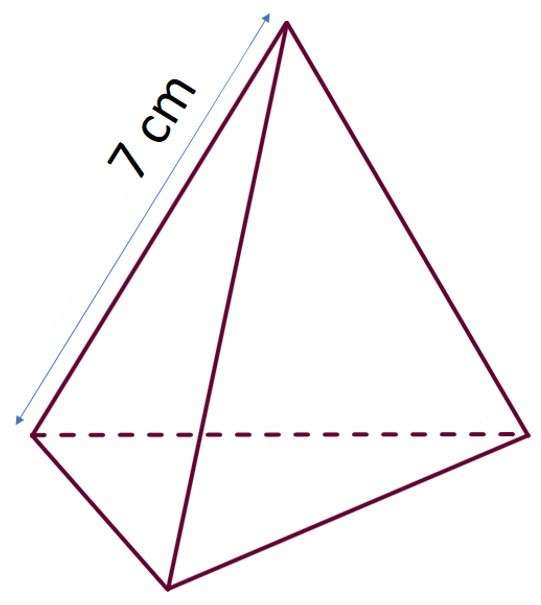
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
b = √(hb2 + a2/4);
b = √(h2 + a2/3).
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
b = √(hb2 + a2/4);
b = √(h2 + a2/2).
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид – это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса

Каждый человек знает, что первое чудо света – пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
b = √(h2 + a2/2).
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
Правильная пирамида – это геометрическое тело, образованное правильным многоугольником, лежащим в основании и боковыми ребрами, подымающимися в одну вершину из всех углов основания. Такая пирамида является типовой, поскольку обладает множеством свойств за счет своего основания. Помимо того, что все боковые грани представляют собой конгруэнтные треугольники, а все боковые ребра равны (также как и ребра в основании между собой), высота правильной пирамиды опускается ровно в центр вписанной и описанной окружностей для заданного многоугольника. Поэтому в такой пирамиде возникает сразу два прямоугольных треугольника во внутреннем пространстве, один из них соединяет высоту с апофемой радиусом вписанной окружности, а второй соединяет высоту с боковым ребром радиусом описанной окружности.
Таким образом, для того, чтобы найти боковое ребро пирамиды, необходимо знать лишь сторону основания, общее количество сторон этого же многоугольника и высоту. По теореме Пифагора, боковое ребро является гипотенузой и, следовательно, находится сложением:
Подставив в формулу значение радиуса описанной окружности для правильного многоугольника, получаем окончательный ее вид: