Всего: 67 1–20 | 21–40 | 41–60 | 61–67
Добавить в вариант
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Источник: Банк заданий ФИПИ
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Всего: 67 1–20 | 21–40 | 41–60 | 61–67
Задание 18.
На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.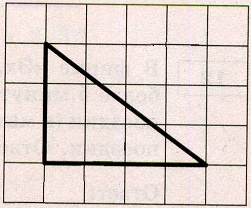
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
Катеты треугольника равны 3 и 4. Больший из них равен 4.

Ответ: 4.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 41
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решение заданий №19(задания на
клетчатой бумаге)
1.Основные типы задач
1.
Определение тангенса угла;
2.
Определение площади фигуры (ромба, трапеции,
параллелограмма, треугольника);
3.
Определение расстояния от точки до прямой
(отрезка);
4.
Определение длины средней линии треугольника и
трапеции;
5.
Определение длины большего катета, большей
диагонали;
6.
Определение площади сложных или составных фигур;
7.
Определение градусной меры вписанного угла.
1.Определение
тангенса угла
Задача
1
Найдите
тангенс угла А треугольника ABC, изображённого
на рисунке 1.
|
Решение:
Ответ: 0,4. |
Рис.1 |
Задача 2
Найдите
тангенс угла AOB, изображённого
на рисунке 3.
|
Решение: 1. Достроим до прямоугольного треугольника СОВ. 2.
Ответ: 2. |
Рис. 3 |
2. Определение площади фигуры
Задача 1
На
клетчатой бумаге с размером клетки 1×1 изображён параллелограмм (рис. 7).
Найдите его площадь.
|
Решение: 1. Проведем высоту. 2. 2. Найдем площадь
Ответ: 10. |
Рис. 7 |
.
Задача 2
На
клетчатой бумаге с размером клетки 1×1 изображён ромб (рис. 9).
Найдите площадь этого ромба.
|
Решение: 1.
2.
Ответ: 30. |
Рис. 9 |
3. Определение расстояния от
точки до прямой (отрезка)
Задача 1
На
клетчатой бумаге с размером клетки 1×1 отмечены три
точки: A, B и C (рис. 11). Найдите расстояние от
точки A до середины отрезка BC.
|
Решение: 1. Построим отрезок ВС и отметим 2. ем
Ответ: |
Рис. 11 |
4. Определение длины средней линии
треугольника и трапеции
Задача 1
На
клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC
(рис. 14). Найдите длину его средней линии, параллельной стороне AC.
|
Решение:
Ответ: |
Рис. 14 |
Задача 2
На
клетчатой бумаге с размером клетки 1×1 изображена трапеция (рис. 15). Найдите
длину её средней линии.
|
Основания Средняя Ответ: |
Рис.15 |
5. Определение длины большего катета, большей диагонали
Задача 1
На
клетчатой бумаге с размером клетки 1×1 изображён прямоугольный
треугольник (рис. 16). Найдите длину его большего катета.
|
Решение: По большего Ответ: |
Рис. 16 |
6. Определение площади сложных
или составных фигур
Задача 1
На
клетчатой бумаге с размером клетки 1×1 изображена фигура (рис. 18). Найдите её
площадь.
|
Решение: Посчитаем Ответ: |
Рис. 18 |
Задача 2
Площадь
одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке
19.
|
Решение: Найдём
Ответ: |
Рис. 19
Рис. 19.1 |
|
Решение: Площадь равна квадрата
Ответ: |
Рис. 19.2 |
Задачи для самостоятельно решения
I.
 Определение
Определение
тангенса угла
1. Найдите тангенс угла А треугольника, изображённого на рисунке.
 |
2. Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
3.  Найдите тангенс угла AOB,
Найдите тангенс угла AOB,
изображённого на рисунке.
4.  Найдите тангенс углаAOB,
Найдите тангенс углаAOB,
изображённого на рисунке.
5.  Найдите тангенс углаAOB,
Найдите тангенс углаAOB,
изображённого на рисунке.
6. Найдите тангенс угла AOB, изображённого на рисунке.
 |
7.  Найдите
Найдите
тангенс углаAOB.
8.  Найдите тангенс углаAOB.
Найдите тангенс углаAOB.
9.  Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
10.
Найдите тангенс угла, изображённого на рисунке.
 |
II.
Определение площади фигуры (ромба, трапеции,
параллелограмма, треугольника)
1. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм.
Найдите его площадь.
 |
2.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображён треугольник. Найдите его площадь.
3. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник.
 |
4.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображён ромб. Найдите его площадь.
5.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
6.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите её площадь.
7.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите её площадь.
III.
Определение расстояния от точки до прямой
(отрезка)
1. На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние от точки А до
прямой ВС. Ответ выразите в сантиметрах.
 |
2.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой ВС.
Ответ выразите в сантиметрах.
3. На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.
 |
4.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1 см × 1 см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
5. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены
точки А, В и С. Найдите расстояние
от точки А до прямой BC. Ответ выразите в сантиметрах.
 |
IV.
Определение длины средней линии треугольника
и трапеции
1.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.
2.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.
3.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.
4.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
5.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
6.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
V.
Определение длины большего катета, большей
диагонали
1.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его
большего катета.
2.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его
большего катета.
3.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его
большего катета.
4. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину
его большей диагонали.
 |
5.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
VI.
Определение площади сложных или составных
фигур
1.  На клетчатой бумаге с размером
На клетчатой бумаге с размером
клетки 1х1 изображена фигура. Найдите её площадь.
2.  На клетчатой бумаге с
На клетчатой бумаге с
размером клетки 1х1 изображена фигура. Найдите её площадь.
3. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её
площадь.
 |
4. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её
площадь.
 |
5.  Площадь одной клетки равна
Площадь одной клетки равна
1. Найдите площадь фигуры, изображённой на рисунке.
6.  Площадь одной клетки равна
Площадь одной клетки равна
1. Найдите площадь фигуры, изображённой на рисунке.
VII.
Определение площади сложных или составных
фигур
1. Найдите угол ABC. Ответ дайте в градусах.
 |
2.  Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
3.  Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
4. Найдите угол ABC. Ответ дайте в градусах.
 |
5. Найдите угол ABC. Ответ дайте в градусах.
 |
6. Найдите угол ABC. Ответ дайте в градусах.
 |
II. Определение площади
фигуры (ромба, трапеции, параллелограмма, треугольника
III. Определение расстояния от точки до
прямой (отрезка)
IV. Определение расстояния от точки до
прямой (отрезка)
V. Определение длины большего катета,
большей диагонали
Всем привет,мои юные и не очень любители пошуршать мозгами! 🧠
Сегодня поговорим о задачах с фигурами,но не простыми,а на квадратной решетке. 🤓
Такого рода задачи часто попадаются на ОГЭ,поэтому рекомендую дочитать ЭТО ЧУДО до конца 🙂
Длина средней линии трапеции
Решим задачу с этой самой длиной. На клетчатой бумаге 1×1 изображена вот такая трапеция:
Найдем длину ее средней линии.
Сосчитаем клеточки оснований:
7 снизу,3 сверху.
Их складываем.
А потом делим ответ на 2:
Ответ: 5
Расстояние от и до
Теперь про более странную задачу поговорим.
На клетчатой бумаге 1×1 отмечены три точки: A,B и C.
Нужно найти расстояние от точки A до середины отрезка BC.
Нужно ПРОСТО сосчитать три клетки до середины! ВСЕ!
Ответ: 3
Площадь ромба
На той же бумаге начертили ромб.
Нужно найти его площадь.
Как? Оч просто!
Нужно сделать из этого ромба прямоугольник:
А теперь посчитаем клеточки у сторон:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 20.
Площадь странной фигуры
На этой же (ОПЯТЬ?!ААА!) бумаге Вася начертил странную фигуру. А мы должны найти ее площадь…)
Теперь внимание! Нужно просто посчитать квадратики! Считаем…
Ответ: 11
Длина большей диагонали ромба
Опять ромб. Только теперь нужно найти не площадь,а длину большей диагонали.
Давайте посчитаем:
Ответ: 8
Повторим расстояния…
Опять нужно найти расстояние от точки А,до прямой BC.
Проведем прямую от точки между точками B и C.
А теперь проведем линию от точки A,до отрезка ВС.
Ответ: 1
Площадь параллелограмма
Найдем площадь параллелограмма.
Как ее искать?
Нужно умножить высоту на основание:
Ответ: 20
Длина средней линии треугольника
У нас есть вот такой треугольник:
Нужно найти длину его средней линии,параллельной стороне AC.
Для этого мы узнаем длину основания и разделим ее на 2.
Ответ: 2
Длина большего катета
Нам дан такой прямоугольный треугольник:
Нужно найти длину его большего катета.
Вспомним про стороны прямоугольного треугольника:
Катет b (основание) больше. Он имеет 10 клеток,а катет а 5.
Ответ: 10.
На этом все!
Ждите более сложные задания в следующем посте!
Как найти стороны прямоугольного треугольника
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Решение №2248 На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник.
Задание 18.
На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Источник: ОГЭ Ященко 2022 (36 вар)
Катеты треугольника равны 3 и 4 . Больший из них равен 4 .
Катеты прямоугольного треугольника – свойства, основные формулы и примеры решений
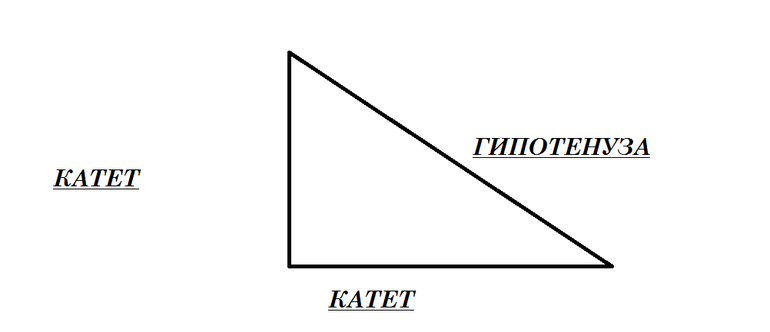
Понятия и определения
Знак треугольника в первом веке ввёл в обиход древнегреческий философ и учёный Герон. Его свойства изучали Платон и Евклид. По их мнению, вся поверхность прямолинейного вида состоит из множеств различных треугольников. В геометрии под ними понимается область, лежащая в плоскости, ограниченной тремя отрезками, соединяющимися в трёх точках, не принадлежащих одной прямой.
Линии, образующие область, называются сторонами, а точки соприкосновения отрезков — вершинами. Основными элементами многоугольника являются:
- Медиана — отрезок, соединяющий середину с противолежащим углом. В треугольнике три медианы, которые пересекаются в одной точке. Называется она центроидом и определяет центр тяжести объекта.
- Высота — линия, опущенная из вершины на противоположную сторону, образующую с ней прямой угол. Место пересечения высот называют ортоцентром.
- Биссектриса — прямая, проведённая из угла таким образом, что делит его на две равные части. Если в треугольник вписать окружность, соприкасающуюся с его сторонами, то её центр совпадёт с точкой пересечения биссектрис. Называют это место — инцентр.
В зависимости от видов углов, треугольники разделяют на остроугольные, тупоугольные и прямоугольные. Но каким бы ни был тип фигуры, существует закономерность, что сумма всех углов всегда равна 180 градусам. Поэтому как минимум два угла должны быть острыми.
Различают треугольники и по числу равных сторон. Так, если они все равны, фигура называется равносторонней. Когда же по величине совпадают только две стороны, то многоугольник является равнобедренным. Его главное свойство в том, что углы равны. Частным случаем равнобедренного многоугольника является правильный треугольник (разносторонний).
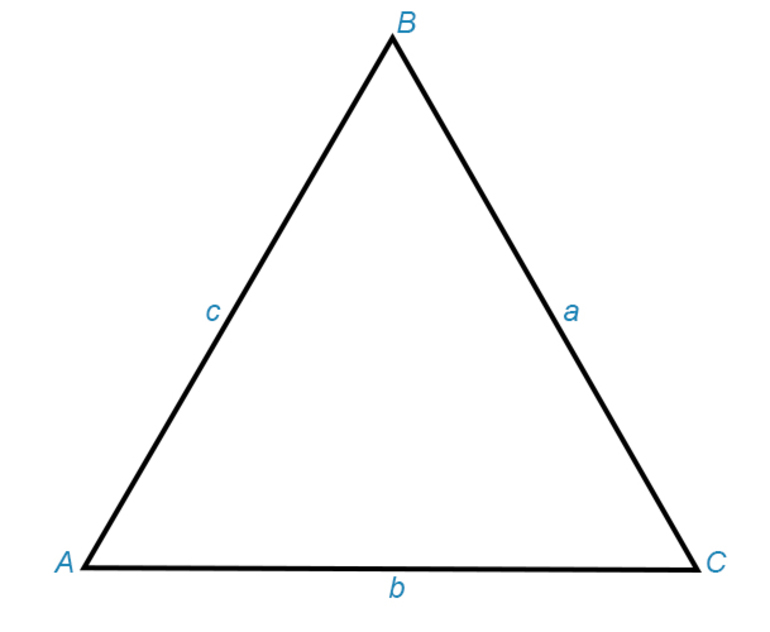
Чтобы не возникала путаница, существуют стандартные обозначения величин. Вершины подписываются заглавными буквами A, B, C, а углы – греческими символами: α, β, γ. Стороны же обозначают прописными буквами латинского алфавита: a, b, c.
Свойства прямоугольного треугольника
Прямоугольный треугольник — это симметричный многоугольник, сумма двух углов которого равняется 90 градусов. Так как общая сумма всех трёх углов составляет 180 градусов, то соответственно третий угол равен 90 градусам. Стороны, образующие его, называют катетами, а оставшийся отрезок гипотенузой.
К основным свойствам фигуры относят следующее:

- гипотенуза многоугольника всегда больше любого из его катетов;
- сторона, располагающаяся напротив угла в 30 градусов, составляет половину гипотенузы;
- два катета являются высотами треугольника;
- середина окружности, описанная вокруг фигуры, совпадает с гипотенузой, при этом медиана, опущенная из прямого угла на гипотенузу, одинаковая с радиусом круга;
- численное значение гипотенузы, возведённое в квадрат, равно сумме квадратов катетов (теорема Пифагора).
Эти основные признаки при решении геометрических задач помогают определить класс треугольника и рассчитать его величины. Большое значение при этом имеет вычисление значений катетов.
Так, если известна гипотенуза, то найти катеты, зная угол, не составит труда. Определив же длину катетов, вычислить оставшуюся сторону можно по теореме Пифагора. Периметр фигуры определяют сложением двух катетов и гипотенузы, а площадь находят перемножением катетов и делением полученного ответа на два.

Зная катеты, довольно просто вычислить угол. Нужно всего лишь запомнить, что соотношение сторон между собой равно тангенсу противолежащего угла и котангенсу, находящемуся рядом. При этом, зная любой из углов, найти второй можно простым вычитанием известного значения из девяноста. Высота же у прямоугольника равна косинусу прилежащего угла.
Формула для нахождения биссектрисы и медианы довольно сложная. Для нахождения первой величины используют преобразование радикала из суммы квадратов катетов к двум, а второй – подстановку радикала вместо стороны, лежащей напротив прямого угла.
Теорема Пифагора и углы
Эта теорема занимает одно из центральных мест в математике. Алгебраическая формулировка её гласит, что в прямоугольнике квадрат длины гипотенузы по своему значению равен сумме квадратов двух прилегающих к ней сторон, то есть катетов. Например, если обозначить гипотенузу буквой c, а катеты а и b, то математически её можно записать в виде формулы: a 2 +b 2 = c 2 .
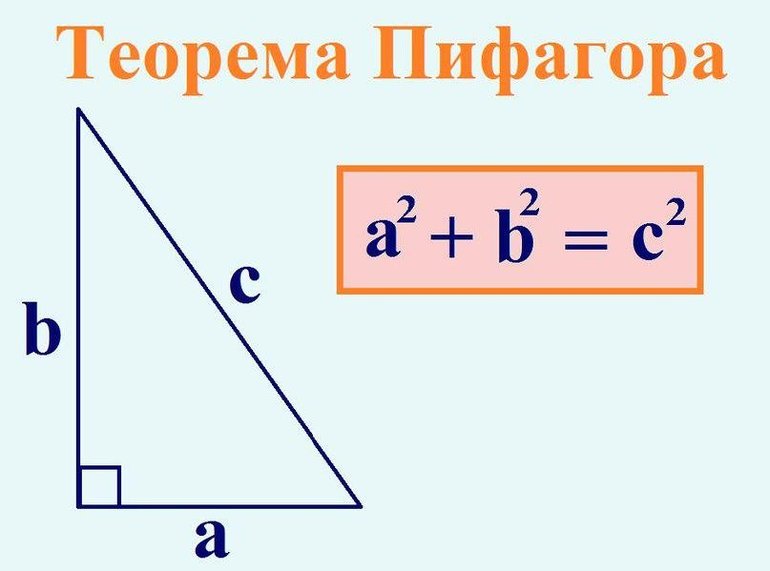
Существует несколько доказательств этой теоремы. Самое простое из них – это использование подобия треугольников. В его основе лежат аксиомы. Пусть имеется геометрическая фигура ABC, у которой вершина C является прямой, то есть её угол равен 90 градусов. Если из точки С опустить высоту, а место пересечения с противолежащей стороной обозначить H, то получится два треугольника. Один будет состоять из вершин AHC, а другой BHC. Эти новые фигуры подобны ABC по двум углам. Следующие выражения будут верными:
Приведённые записи эквивалентны равенствам: BC 2 = AB * HB; AC 2 = AB * AH. Сложив первую и вторую формулу, получается: BC 2 + AC 2 = AB * (HB + AH) = AB 2 . Что и следовало доказать.
Используя это фундаментальное правило и свойство, что катет, расположенный напротив угла в 30 градусов, равен половине гипотенузы, проводят множество расчётов, связанных с вычислением длин сторон. Для доказательства, что AC = BC/2, приводят следующие рассуждения.
Так как вершина B равна 30 градусам, то, согласно правилу, разворот С должен составлять C =30*2 = 60 градусов. К имеющемуся треугольнику можно приложить точно такую же фигуру, делая сторону AB центром симметрии. Тогда для многоугольника BCD будет справедливо, что B = D = 60º. Исходя из этого можно утверждать, что DC = BC. Но, так как AC = ½ DC, то соответственно AC = ½ BC.
Но не всегда известны все данные, необходимые для нахождения длины катета по приведённым теоремам. Поэтому для вычисления катетов используются и тригонометрические соотношения.
Тригонометрические формулы
Для нахождения длины катета прямоугольного треугольника используют простые формулы. Для их применения нужно знать значение любой из сторон и величину разворота произвольной вершины. Существует четыре способа, позволяющих найти катет с использованием тригонометрических правил:

- В основе лежит аксиома, что синус находится из отношения противолежащего катета к гипотенузе. Например, пусть известно что длина гипотенузы составляет 100 сантиметров, а вершина A имеет разворот равный 30 градусам. Используя тригонометрические таблицы, можно утверждать, что синус угла A составляет ½. Учитывая преобразованное выражение, находят катет: a = 100 / 2 =50 (см). Таким образом, синус острого угла численно равен отношению одного из катетов, деленного на гипотенузу: sin A = BC/AB.
- Используется правило, что косинус в прямоугольнике представляет собой отношение прилежащего катета к прямому углу и гипотенузе: cosA = AC/AB. Например, пусть разворот вершины C равен 60 градусам, а гипотенуза равна 100 сантиметрам. Согласно тригонометрической таблице, угол в 60 градусов равен ½. Подставив это значение в формулу, можно найти значение катета: a=cos∠C*a; b=½*100=50 сантиметров.
- Тангенс угла можно вычислить, разделив значение длины противолежащего катета к прилежащему. Математическая формула этого утверждения имеет вид: tg = BC/AC. Катет многоугольника может быть найден как b = tg * a. Например, известно, что у фигуры один из углов равен 45 градусов, а длина гипотенузы составляет 100 сантиметров. Так как тангенс 45 градусов равен единице, то ответом на задачу будет: a = 1*100 = 100 сантиметров.
- Котангенс определяется из соотношения прилежащего катета к противолежащему. Фактически это величина, обратная тангенсу: ctg = AC/BC. Например, пусть разворот угла A составляет 30 градусов, а длина катета, находящегося напротив него, равняется 50 сантиметрам. Котангенс 30 градусов соответствует корню из трёх. Подставив в формулу известные данные, можно вычислить неизвестный катет: b =50√3 сантиметров.
Зная, как выглядят тригонометрические формулы и содержание двух теорем, вычислить значение катета можно будет в большинстве поставленных задач.
Типовые примеры
Для решения задач на нахождение катета не нужно обладать какими-то особенными знаниями. Нужно просто внимательно проанализировать условие. Например, пусть известно, что в прямоугольнике один катет длиннее другого на пять сантиметров. При этом площадь фигуры равняется 84 сантиметрам в квадрате. Необходимо определить длины сторон и периметр.
Так как в условии дана площадь, то при решении необходимо отталкиваться от неё. Известно, что площадь прямоугольного треугольника находится по формуле: S = AC*CB/2. Это выражение является частным случаем общей формулы для нахождения площади любого треугольника, где: AC — это высота, а CB — основание. Если принять, что AC равно X, то, согласно условию, длина CB будет составлять x+5.

Исходя из этого, площадь треугольника будет равна: S = (x*(x+5))/2. Подставив вместо S заданное значение, можно получить квадратное уравнение: x2 + 5x — 84 = 0. Решать его лучше методом детерминанта. Корнями уравнения будут -12 и 7. Так как -12 не удовлетворяет условию задачи, то верным ответом будет семь.
Длина второго катета равняется семи сантиметрам. Первого: AC = 7−5 = 2 см. Зная оба катета, по теореме Пифагора можно найти гипотенузу: c = (22 + 72)½ = (4+49)½ = 531/2 = 7,3 см. Найдя длины всех сторон, можно без усилий найти периметр обыкновенным сложением: P = 2+7+7,3 = 16,3 см. Задача решена.
Довольно интересные, но в то же время простые задачи на нахождение сторон и углов при известной длине гипотенузы и значения разворота одной из вершин. Пусть имеется прямоугольный треугольник, у которого гипотенуза BC равняется пяти сантиметрам, а угол между ней и катетом составляет 60 градусов. Нужно определить все остальные стороны и углы.
Так как известна гипотенуза и острый угол, то, воспользовавшись тригонометрическими формулами, можно найти длины катетов: AC=BC*sin60 = 5*(3) ½ /2; AB=BC*cos60 = 5/2. Сумма всех углов в треугольнике равна 180 градусов, так как один из них прямой, а второй задан и составляет 60 градусов, то третий находится путём вычитания C = 180 – (90 + 60) = 30.
[spoiler title=”источники:”]
http://nauka.club/matematika/katet-v-pryamougolnom-treugolnike.html
[/spoiler]

















