Треугольник. Расчет сторон прямоугольного треугольника через тригонометрические функции.
Проанализируем прямоугольный треугольник ABC в котором обозначим катеты как а, b и гипотенузу как с соответственно.
Вполне логично сделать вывод, будут верны следующие равенства:
Значит катет прямоугольного треугольника допускается представить как произведение гипотенузы и синуса угла, противолежащего этому катету, либо и косинуса угла, прилежащего к нему.
На основе этих соотношений так же можно определить гипотенузу прямоугольного треугольника:
Иначе говоря, гипотенуза будет частным от деления катета либо на синус противолежащего к нему угла, либо на косинус прилежащего к катету угла.
Значит, катет прямоугольного треугольника допускается представить как произведением другого катета на тангенс угла, противолежащего первому катету, либо на котангенс угла, прилежащего к первому катету.
Как с помощью тангенса найти сторону треугольника. Теорема Пифагора, чтобы найти катет прямоугольного треугольника
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).


Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.


Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).


Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).


Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).


Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).


Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Сторону треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции – синус и косинус . Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
1. Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус ом и косинус ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам. Треугольник НBC показан на рисунке. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
2. Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
3. В элементарной математике существует представление теоремы синус ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin ?=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда знамениты две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
4. Помимо теоремы синус ов, существует и аналогичная ей по сути теорема косинус ов, которая, как и предыдущая, также применима к треугольникам всех 3 разновидностей: прямоугольному, остроугольному и тупоугольному. Руководствуясь фактами, которые доказывают эта теорема, дозволено находить неведомые величины, применяя следующие соотношения между ними:c^2=a^2+b^2-2ab*cos ?
Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум углам .

Инструкция
1. Пускай построен треугольник?ABC и знамениты – сторона BC и углы?? и. Знаменито, что сумма углов всякого треугольника равна 180?, следственно в треугольнике?ABC угол?? будет равен?? = 180? – (?? + ??).Обнаружить стороны AC и AB дозволено применяя теорему синусов, которая гласитAB/sin?? = BC/sin?? = AC/sin?? = 2 * R, где R – радиус описанной около треугольника?ABC окружности,тогда получаемR = BC/sin. AB = 2 * R * sin. AC = 2 * R * sin. Теорему синусов дозволено использовать при всяких данных 2-х углах и стороне.

2. Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin. где R вычисляется по формулеR = BC/sin. R – радиус описанной около треугольника?ABC отсюдаТогда сторону AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin. отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить сторону AC.

3. Если в качестве углов даны внешние углы треугольника?? и. то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – . = 180? – . = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.

Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.

Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках. Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S – площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h , где h – это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
Решение задач
Задача 1. Найти площадь треугольника ABC, если а) AB = 6*√8 см, АС = 4 см, угол А = 60 градусов б) BC = 3 см, AB = 18*√2 см, угол B= 45 градусов в) AC = 14 см, CB = 7 см, угол C= 48 градусов.
По доказанной выше теореме площадь S треугольника ABC равна:
а) S = ((1/2) *6*√8*4*sin(60˚)) = 12*√6 см^2.
б) S = (1/2)*BC*BA*sin(B)=((1/2)* 3*18*√2 *(√2/2)) = 27 см^2.
в) S = (1/2)*CA*CB*sin(C) = ½*14*7*sin48˚ см^2.
Значение синуса угла считаем на калькуляторе либо используем значения из таблицы значений тригонометрических углов. Ответ:
в) приблизительно 36.41 см^2.
Задача 2. Площадь треугольника ABC равна 60 см^2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
Положим S – площадь треугольника ABC. По теореме о площади треугольника имеем:
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону – гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.

Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.

Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс – функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.

Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.

Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то: 
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: 
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем
Понравилось?
Нажмите на кнопку, если статья Вам понравилась, это поможет нам развивать проект. Спасибо!
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://school10-mgn.ru/kak-s-pomoshchyu-tangensa-naiti-storonu-treugolnika-teorema-pifagora.html
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Пусть a, b — катеты, с — гипотенуза, d — угол между c и a. Причём, a и tg(d) известны; найти требуется b и c.
По геометрическому смыслу синуса, катет b, противолежащий углу d равен b=c*sin(d). Аналогично для косинуса и прилежащего катета: a=c*cos(d). Если разделим эти равенства друг на друга, получим b/a=sin(d)/cos(d). Но, известно, что tg(d)=sin(d)/cos(d) (это, фактически, определение тангенса), поэтому b/a=tg(d), откуда b=a*tg(d).
В прямоугольном треугольнике выполняется cc=aa+bb. Подставляя сюда ранееполученное выражение для b, получаем cc = aa+aa*tg(d)*tg(d) = aa(1+tg(d)*tg(d)). Так что, в итоге, если я ничего не напутал, то c=a*sqrt(1+tg(d)*tg(d)), где sqrt() — квадратный корень.
Если же вместо a известен катет b, то в выражении b=a*tg(d) надо “поменять местами” b и a: a=b/tg(d). В этом случае, из cc=aa+bb следует cc = bb(1+1/(tg(d)*tg(d))) => c=b*sqrt(1+1/(tg(d)*tg(d))).
N.B.: По отношению к рисунку из соседнего ответа, в моём катеты a и b перепутаны местами; но, в любом случае, неизвестное выражается через известное. 🙂
Интересно, на БВ когда-нибудь появится нормальная поддержка математических формул? 🙂 Вот разве плохо бы было, если бы ответ был представлен как-то так:

Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):


Формулы длины равных сторон , (a):


Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
 H – высота треугольника
H – высота треугольника
a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Калькулятор – вычислить, найти медиану, биссектрису, высоту
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):



Формула высоты, биссектрисы и медианы, через стороны, (L):

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):


Формула длины биссектрисы через катет и гипотенузу, (L):


L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):


Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Катетами прямоугольного треугольника называются те его стороны, которые образуют прямой угол. Каждый из катетов всегда меньше гипотенузы по значению, но в сумме они обязательно ее превосходят. Зная оба катета, можно найти не только третью сторону прямоугольного треугольника – гипотенузу, по теореме Пифагора, но и углы, находящиеся между катетами и гипотенузой. Для этого используется тригонометрическое отношение тангенса угла α, которое по определению равно отношению катета, противолежащего углу α, к катету прилежащему.

Делением катета, находящегося напротив угла, на катет, который является одной из сторон угла, получается значение тангенса, соответствующее определенной градусной мере. Краткая таблица основных значений тангенса находится внизу страницы, а полная таблица всех тангенсов расположена по ссылке.

Свойства
Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету b.

Таблица тангенсов
| Тангенс угла 0° градусов | 0 | 0.000 |
| Тангенс угла 30° градусов | 1/√3 | 0.577 |
| Тангенс угла 45° градусов | 1 | 1.000 |
| Тангенс угла 60° градусов | √3 | 1.732 |
| Тангенс угла 90° градусов | ∞ | ∞ |
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
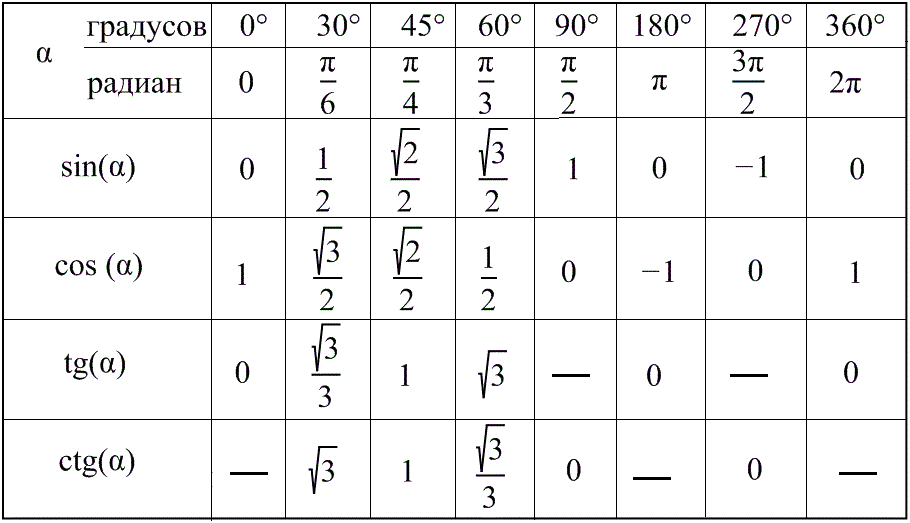
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
