Как найти длину действительной оси гиперболы - Сайт, где вы сможете решить свои вопросы

Гипербола: формулы, примеры решения задач

Определение гиперболы, решаем задачи вместе

Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы имеет вид:

где a и b – длины полуосей, действительной и мнимой.

На чертеже ниже фокусы обозначены как и .

На чертеже ветви гиперболы – бордового цвета.

При a = b гипербола называется равносторонней.

Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.

Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.

Точки и , где

называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).

называется эксцентриситетом гиперболы.

Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.

Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.

Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,

Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.

То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.

Подставляем и вычисляем:

Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .

Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет – это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат – каноническое уравнение гиперболы:

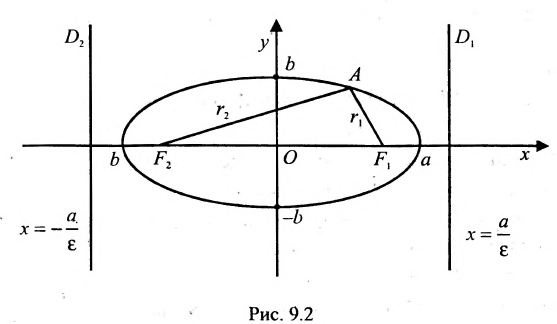
Если – произвольная точка левой ветви гиперболы () и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:

Если – произвольная точка правой ветви гиперболы () и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:

На чертеже расстояния обозначены оранжевыми линиями.

Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже – прямые ярко-красного цвета).

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где – расстояние от левого фокуса до точки любой ветви гиперболы, – расстояние от правого фокуса до точки любой ветви гиперболы и и – расстояния этой точки до директрис и .

Пример 4. Дана гипербола . Составить уравнение её директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:

Получаем уравнение директрис гиперболы:

Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке “Эллипс” это пример 7.

Характерной особенностью гиперболы является наличие асимптот – прямых, к которым приближаются точки гиперболы при удалении от центра.

Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты – прямые серого цвета, проходящие через начало координат O.

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:

, где .

В том случае, когда угол между асимптотами – прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.

Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.

Решение. Дробь в уравнении асимптот гиперболы – это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:

Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) b = 4 , а один из фокусов в точке (5; 0)

2) действительная ось 6, расстояние между фокусами 8

3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы

Гипербола – определение и вычисление с примерами решения

Гипербола:

Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек

Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы

Рис. 31. Вывод уравнения гиперболы.

Расстояние между фокусами (фокусное расстояние) равно Согласно определению, для гиперболы имеем Из треугольников по теореме Пифагора найдем соответственно.

Следовательно, согласно определению имеем

Возведем обе части равенства в квадрат, получим

Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Получим Разделив все члены уравнения на величину получаем каноническое уравнение гиперболы: Для знака “+” фокусы гиперболы расположены на оси Ох, вдоль которой вытянута гипербола. Для знака фокусы гиперболы расположены на оси Оу, вдоль которой вытянута гипербола.

Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки и следовательно, гипербола симметрична относительно координатных осей, которые в данном случае будут называться осями симметрии гиперболы (Рис. 32). Найдем координаты точек пересечения гиперболы с координатными осями: т.е. точками пересечения гиперболы с осью абсцисс будут точки т.е. гипербола не пересекает ось ординат.

Рис. 32. Асимптоты и параметры гиперболы

Определение: Найденные точки называются вершинами гиперболы.

Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым не пересекая эти прямые. Из уравнения гиперболы находим, что При неограниченном росте (убывании) переменной х величина следовательно, гипербола будет неограниченно приближаться к прямым

Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.

В данном конкретном случае параметр а называется действительной, а параметр b – мнимой полуосями гиперболы.

Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы

Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси Если эксцентриситет и гипербола становится равнобочной. Если и гипербола вырождается в два полубесконечных отрезка

Пример:

Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).

Решение:

Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:

Следовательно, каноническое уравнение гиперболы имеет вид

Пример:

Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах эллипса

Решение:

Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: или Следовательно, большая полуось эллипса а малая полуось Итак, вершины эллипса расположены на оси и на оси Так как то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса Итак, Согласно условию задачи (см. Рис. 33):

Рис. 33. Параметры эллипса и гиперболы

Вычислим длину мнимой полуоси Уравнение гиперболы имеет вид:

Гипербола в высшей математике

Решая его относительно , получим две явные функции

или одну двузначную функцию

Функция имеет действительные значения только в том случае, если . При функция действительных значений не имеет. Следовательно, если , то точек с координатами, удовлетворяющими уравнению (3), не существует.

При получаем.

При каждому значению соответствуют два значения , поэтому кривая симметрична относительно оси . Так же можно убедиться в симметрии относительно оси . Поэтому в рассуждениях можно ограничиться рассмотрением только первой четверти. В этой четверти при увеличении х значение у будет также увеличиваться (рис. 36).

Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.

Гипербола в силу симметрии имеет вид, указанный на рис. 37.

Точки пересечения гиперболы с осью называются вершинами гиперболы; на рис. 37 они обозначены буквами и .

Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.

Рассмотрим прямую, заданную уравнением . Чтобы не смешивать ординату точки, расположенной на этой прямой, с ординатой точки, расположенной на гиперболе, будем обозначать ординату точки на прямой , а ординату точки на гиперболе через . Тогда , (рассматриваем только кусок правой ветви, расположенной в первой четверти). Найдем разность ординат точек, взятых на прямой и на гиперболе при одинаковых абсциссах:

Умножим и разделим правую часть на

Будем придавать все большие и большие значения, тогда правая часть равенства будет становиться все меньше и меньше, приближаясь к нулю. Следовательно, разность будет приближаться к нулю, а это значит, что точки, расположенные на прямой и гиперболе, будут сближаться. Таким образом, можно сказать, что рассматриваемая часть правой ветви гиперболы по мере удаления от начала координат приближается к прямой .

Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением . Также кусок левой ветви, расположенный во второй четверти, приближается к прямой , а кусок левой ветви, расположенный в третьей четверти, — к прямой .

Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.

Таким образом, гипербола имеет две асимптоты, определяемые уравнениями (рис. 37).

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Парабола
Многогранник
Решение задач на вычисление площадей
Тела вращения: цилиндр, конус, шар
Правильные многогранники в геометрии
Многогранники
Окружность
Эллипс

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Как найти координаты фокусов гиперболы

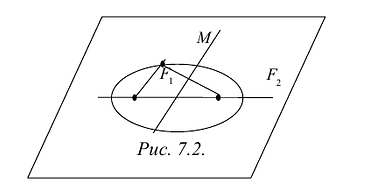
Гиперболой Называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим эту постоянную через 2А, расстояние между фокусами через 2С, а оси координат выберем так же, как в разделе 2.3.

Пусть М(Х, У) – произвольная точка гиперболы (рисунок 2.4).

По определению гиперболы F2M – F1М = ±2A. (Знак плюс в правой части надо выбрать, если F2M > F1М, и минус, если F2M A).

Исследуем формулу гиперболы.

1. Уравнение (2.7) содержит квадраты текущих координат, следовательно, оси координат являются осями симметрии гиперболы. Ось симметрии, на которой находятся фокусы, называется фокальной осью, точка пересечения осей симметрии – центром гиперболы. Для гиперболы, заданной уравнением (2.7), фокальная ось совпадает с осью ОХ, а центр – с началом координат.

В этом случае координаты фокусов гиперболы имеют вид F1(с,0), F2(-с,0).

2. Точки пересечения с осями симметрии. Точки пересечения гиперболы с осями симметрии называются Вершинами гиперболы. Полагая в уравнении (2.7) У = 0, найдем абсциссы точек пересечения с осью ОХ:

или X2 = А2, откуда Х = ±А.

Итак, точки и являются вершинами гиперболы.

Если же в уравнении (2.7) принять x = 0, получим

или У2 = –B2,

Т. е. для У мы получили мнимые значения. Это означает, что гипербола не пересекает ось ОY.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью (фокальная ось); ось симметрии, которая не пересекает гиперболу, – ее мнимой осью. Для гиперболы, заданной уравнением (2.7), действительной осью симметрии является ось ОХ, а мнимой осью – ось ОY. Длина отрезка А1А2 = 2А, число А называется действительной полуосью гиперболы. Отложим на мнимой оси гиперболы по обе стороны от центра симметрии O отрезки ОВ1 и ОВ2 длиною B, тогда отрезок В1B2 = 2B называют мнимой осью, а величину B – мнимой полуосью гиперболы.

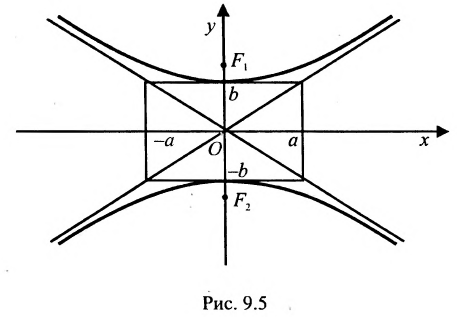
Из уравнения (2.7) видно, что , следовательно, |X| ³ A. Кривая имеет форму, изображенную на рисунке 2.5. Она располагается вне прямоугольника со сторонами, равными 2А и 2B, с центром в начале координат, и состоит из двух отдельных ветвей, простирающихся в бесконечность (см. рисунок 2.5). Диагонали этого прямоугольника определяются уравнениями

(2.8)

И являются Асимптотами гиперболы.

Если A = B, гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна 2А и расположена на оси ОХ, а действи-тельная ось равна 2B и расположена на оси ОY, то уравнение такой гиперболы (рисунок 2.6) имеет вид (каноническое уравнение гиперболы, если ее фокальная ось – ось Y)

(2.9)

Координаты фокусов в этом случае имеет вид F1(0,с) и F2(0,-с).

Гиперболы (2.7) и (2.9) называются Сопряженными гиперболами.

Замечание 2. Эксцентриситетом Гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы

(2.10)

Для любой гиперболы ε > 1, это число определяет форму гиперболы.

Пример 2.3. Найти координаты фокусов и вершин гиперболы

Написать уравнение ее асимптот и вычислить эксцентриситет.

Решение. Напишем каноническое уравнение гиперболы, для чего обе части уравнения поделим на 144. После сокращения получим

Отсюда видно, что А2 = 9, т. е. A = 3 и B2 = 16, т. е. B = 4.

Для гиперболы С2 = А2 + B2 = 16 + 9 = 25, отсюда C = 5.

Теперь можем написать координаты вершин и фокусов гиперболы:

Эксцентриситет , а уравнения асимптот имеют вид

и .

Определение гиперболы, решаем задачи вместе

Каноническое уравнение гиперболы имеет вид:

где a и b – длины полуосей, действительной и мнимой.

На чертеже ниже фокусы обозначены как и .

На чертеже ветви гиперболы – бордового цвета.

При a = b гипербола называется равносторонней.

Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.

Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки и , где

называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).

называется эксцентриситетом гиперболы.

Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.

Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,

Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.

То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.

Подставляем и вычисляем:

Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Результат – каноническое уравнение гиперболы:

На чертеже расстояния обозначены оранжевыми линиями.

Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже – прямые ярко-красного цвета).

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

Пример 4. Дана гипербола . Составить уравнение её директрис.

Получаем уравнение директрис гиперболы:

Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты – прямые серого цвета, проходящие через начало координат O.

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:

, где .

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

1) b = 4 , а один из фокусов в точке (5; 0)

2) действительная ось 6, расстояние между фокусами 8

3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

По определению | r ₁ – r ₂ | = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М(х, у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью.

Ось 2 b называется мнимой осью.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения:

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

Из очевидных геометрических соотношений можно записать:

a / e + d = x , следовательно d = x – a / e .

( x – c ) 2 + y 2 = r 2

Из канонического уравнения: , с учетом b 2 = c 2 – a 2 :

Тогда т.к. с/ a = e , то r = ex – a .

Итого:

Для левой ветви доказательство аналогично. Теорема доказана

Пример 1 . Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса

Для эллипса: c 2 = a 2 – b 2 . Для гиперболы: c 2 = a 2 + b 2 .

Уравнение гиперболы:

Пример 2 . Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением

Находим фокусное расстояние c 2 = 25 – 9 = 16.

Для гиперболы: c 2 = a 2 + b 2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a 2 ; a 2 = 4;

[spoiler title=”источники:”]

http://www.evkova.org/giperbola

http://dudom.ru/kompjutery/kak-najti-koordinaty-fokusov-giperboly/

[/spoiler]

Источник

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F_1 и F_2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки F_1 и F_2 называются фокусами гиперболы, расстояние 2c=F_1F_2 между ними — фокусным расстоянием, середина отрезка F_1F_2 — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки F_1M и F_2M , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение $e=frac{c}{a}$ , где $c=sqrt{a^2+b^2}$ , называется эксцентриситетом гиперболы. Из определения (2a<2c) следует, что e>1 .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Гипербола и фокальное свойство гипербол

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0) и F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей гиперболе, имеем:

$left||overrightarrow{F_1M}|-|overrightarrow{F_2M}|right|=2a.$

Записывая это уравнение в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}-sqrt{(x-c)^2+y^2}=pm2a.$

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1,,$

где $b=sqrt{c^2-a^2}$ , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $a^2!!not{phantom{|}},c$ от нее (рис.3.41,а). При a=0 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом e=1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

Директрисы гиперболы и директориальное свойство

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.41,а) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=eleft(x-frac{a^2}{c}right)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~c^2-a^2=b^2$ , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1 :

$frac{r_1}{rho_1}=e quad Leftrightarrow quad sqrt{(x+c)^2+y^2}= eleft(x+frac{a^2}{c} right).$

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат F_2rvarphi (рис.3.41,б) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$ , где $p=frac{p^2}{a}$ — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус F_2 гиперболы, а в качестве полярной оси — луч с началом в точке F_2 , принадлежащий прямой F_1F_2 , но не содержащий точки F_1 (рис.3.41,б). Тогда для произвольной точки M(r,varphi) , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем F_1M-r=2a . Выражаем расстояние между точками M(r,varphi) и F_1(2c,pi) (см. пункт 2 замечаний 2.8):

$F_1M=sqrt{(2c)^2+r^2-2cdot(2c)^2cdot rcdotcos(varphi-pi)}=sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}.$

Следовательно, в координатной форме уравнение гиперболы имеет вид

$sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}-r=2a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2+4crcdotcosvarphi+4c^2=4a^2+4ar+r^2 quad Leftrightarrow quad aleft(1-frac{c}{a}cosvarphiright)r=c^2-a^2.$

Выражаем полярный радиус и делаем замены $e=frac{c}{a},~b^2=c^2-a^2,~p=frac{b^2}{a}$ :

$r=frac{c^2-a^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{b^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecosvarphi},$

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( e>1 для гиперболы, 0leqslant e<1 для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0 , находим абсциссы точек пересечения: x=pm a . Следовательно, вершины имеют координаты (-a,0),,(a,0) . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя x=0 , получаем y=pm ib . Длина отрезка оси ординат, соединяющего точки (0,-b),,(0,b) , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые $y=pmfrac{b}{a},x$ , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ (т.е. при a=b ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат Ox'y' (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид $y'=frac{a^2}{2x'}$ (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

Асимптоты гиперболы и равносторонняя гипербола

В самом деле, повернем каноническую систему координат на угол $varphi=-frac{pi}{4}$ (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

$left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y',\ y&=-frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y'end{aligned}right. quad Leftrightarrow quad left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot(x'+y'),\ y&=frac{sqrt{2}}{2}cdot(y'-x')end{aligned}right.$

Подставляя эти выражения в уравнение $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ равносторонней гиперболы и приводя подобные члены, получаем

$frac{frac{1}{2}(x'+y')^2}{a^2}-frac{frac{1}{2}(y'-x')^2}{a^2}=1 quad Leftrightarrow quad 2cdot x'cdot y'=a^2 quad Leftrightarrow quad y'=frac{a^2}{2cdot x'}.$

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит гиперболе $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ . то и точки M'(x,y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах $r=frac{p}{1-ecosvarphi}$ (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина gamma угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: $operatorname{tg}frac{gamma}{2}=frac{b}{2}$ . Учитывая, что $e=frac{c}{a}$ и c^2=a^2+b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2+b^2}{a^2}=1+{left(frac{b}{a}right)!}^2=1+operatorname{tg}^2frac{gamma}{2}.$

Чем больше , тем больше угол gamma . Для равносторонней гиперболы (a=b) имеем e=sqrt{2} и $gamma=frac{pi}{2}$ . Для e>sqrt{2} угол gamma тупой, а для 1<e<sqrt{2} угол gamma острый (рис.3.43,а).

Эксцентриситет гиперболы и сопряжённая гипербола

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ и $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}-frac{(y-y_0)^2}{b^2}=1$ определяет гиперболу с центром в точке O'(x_0,y_0) , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение $-frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1$ определяет сопряженную гиперболу с центром в точке O'(x_0,y_0) .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

$begin{cases}x=acdotoperatorname{ch}t,\y=bcdotoperatorname{sh}t,end{cases}tinmathbb{R},$

где $operatorname{ch}t=frac{e^t+e^{-t}}{2}$ — гиперболический косинус, a $operatorname{sh}t=frac{e^t-e^{-t}}{2}$ гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству $operatorname{ch}^2t-operatorname{sh}^2t=1$ .

Построение гиперболы в канонической системе координат

Пример 3.21. Изобразить гиперболу $frac{x^2}{2^2}-frac{y^2}{3^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — действительная полуось, b=3 — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами 2a=4,~2b=6 с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя x=4 в уравнение гиперболы, получаем

$frac{4^2}{2^2}-frac{y^2}{3^2}=1 quad Leftrightarrow quad y^2=27 quad Leftrightarrow quad y=pm3sqrt{3}.$

Следовательно, точки с координатами (4;3sqrt{3}) и (4;-3sqrt{3}) принадлежат гиперболе. Вычисляем фокусное расстояние

$2cdot c=2cdotsqrt{a^2+b^2}=2cdotsqrt{2^2+3^2}=2sqrt{13}$

эксцентриситет $e=frac{c}{a}=frac{sqrt{13}}{2}$ ; фокальныи параметр $p=frac{b^2}{a}=frac{3^2}{2}=4,!5$ . Составляем уравнения асимптот $y=pmfrac{b}{a},x$ , то есть $y=pmfrac{3}{2},x$ , и уравнения директрис: $x=pmfrac{a^2}{c}=frac{4}{sqrt{13}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

У этого термина существуют и другие значения, см. Гипербола.

Сечения конусов плоскостью (с эксцентриситетом, большим единицы)

Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек $F_{1}$ и $F_{2}$ (называемых фокусами) постоянно. Точнее,

${bigl |}|F_{1}M|-|F_{2}M|{bigr |}=2a,$

причём $|F_{1}F_{2}|>2a>0.$

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.

История[править | править код]

Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Определения[править | править код]

Гипербола может быть определена несколькими путями.

Коническое сечение[править | править код]

Три основных конических сечения

Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

Как геометрическое место точек[править | править код]

Через фокусы[править | править код]

Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.

Через директрису и фокус[править | править код]

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.

Связанные определения[править | править код]

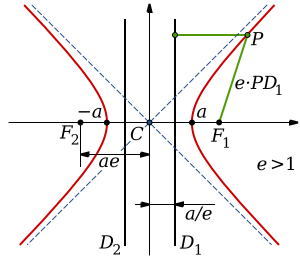
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F₁ и F₂. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D₁ и D₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:

a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов, F₁ и F₂,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами

Гипербола состоит из двух отдельных кривых, которые называют ветвями.
Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
Середина большой оси называется центром гиперболы.
Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
- Обычно обозначается c.
Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной, или поперечной, осью гиперболы.
Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой, или сопряжённой, осью гиперболы.
Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается $r_{p}$ .

Соотношения[править | править код]

Для характеристик гиперболы, определённых выше, существуют следующие соотношения

${displaystyle c^{2}=a^{2}+b^{2}}$ .
.
${displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}$ .
${displaystyle r_{p}=aleft(varepsilon -1right)}$ .
${displaystyle a={frac {p}{varepsilon ^{2}-1}}}$ .
${displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}$ .
${displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}$ .
$p={frac {b^{2}}{a}}$ .

Равнобочная гипербола[править | править код]

Гиперболу, у которой a=b , называют равнобочной, или равносторонней.
Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

$xy=a^{2}/2,$

при этом фокусы гиперболы располагаются в точках (a, a) и (−a, −a).
Равнобочная гипербола является графиком обратной пропорциональности, задаваемой формулой

${displaystyle y={frac {k}{x}},quad kneq 0.}$

Эксцентриситет такой гиперболы равен .

Гипербола Киперта[править | править код]

Точка на гиперболе Киперта

Равнобочная гипербола как гипербола Киперта может быть определена через треугольники в трилинейных координатах^[1] в виде геометрического места точек (см. рис.):

Если три треугольника , и построены на сторонах треугольника , являются подобными, равнобедренными с основаниями на сторонах исходного треугольника, и одинаково расположенными (то есть все они построены либо с внешней стороны, либо с внутренней стороны), то прямые , и пересекаются в одной точке .

Если общий угол при основании равен theta , то вершины трёх треугольников имеют следующие трилинейные координаты:

{displaystyle X{big (}-sin theta :sin(C+theta ):sin(B+theta ){big )},}

{displaystyle Y{big (}sin(C+theta ):-sin theta :sin(A+theta ){big )},}

{displaystyle Z{big (}sin(B+theta ):sin(A+theta ):-sin theta {big )}.}

Уравнения[править | править код]

Декартовы координаты[править | править код]

Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

$A_{{xx}}x^{{2}}+2A_{{xy}}xy+A_{{yy}}y^{{2}}+2B_{{x}}x+2B_{{y}}y+C,=,0$

где коэффициенты A_xx, A_xy, A_yy, B_x, B_y, и C удовлетворяют следующему соотношению

${displaystyle D={begin{vmatrix}A_{xx}&A_{xy}\A_{xy}&A_{yy}end{vmatrix}}<0}$

$Delta :={begin{vmatrix}A_{{xx}}&A_{{xy}}&B_{{x}}\A_{{xy}}&A_{{yy}}&B_{{y}}\B_{{x}}&B_{{y}}&Cend{vmatrix}}not =0.$

Канонический вид[править | править код]

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду:

${frac {{x}^{{2}}}{a^{{2}}}}-{frac {{y}^{{2}}}{b^{{2}}}}=1$

где — действительная полуось гиперболы; — мнимая полуось гиперболы^[2]. В этом случае эксцентриситет равен

${displaystyle varepsilon ={frac {c}{a}}={sqrt {1+{frac {b^{2}}{a^{2}}}}}.}$

Полярные координаты[править | править код]

Гипербола в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

$r={frac {p}{1-varepsilon cos varphi }}$

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

${frac {1}{r}}={frac {a}{b^{2}}}left(1-cos theta right)+{frac {1}{b}}sin theta$

Уравнения в параметрической форме[править | править код]

Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции^[3].

${displaystyle {begin{cases}x=pm aoperatorname {ch} t,\y=boperatorname {sh} t,end{cases}}quad -infty <t<+infty .}$

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «−» — её левой ветви.

Свойства[править | править код]

Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при .
Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.

Асимптоты[править | править код]

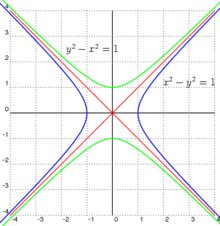
Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Уравнения асимптот для гиперболы, заданной в каноническом виде

${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1$

выводятся следующим образом. Пусть . Предположим, что асимптота существует и имеет вид . Тогда

${displaystyle k=lim _{xto +infty }{frac {f(x)}{x}}=lim _{xto +infty }{frac {{frac {b}{a}}{sqrt {x^{2}-a^{2}}}}{x}}=lim _{xto +infty }{frac {b}{a}}left({frac {sqrt {x^{2}-a^{2}}}{x}}right)=lim _{xto +infty }{frac {b}{a}}left({sqrt {1-{frac {a^{2}}{x^{2}}}}}right)={frac {b}{a}},}$

${displaystyle l=lim _{xto +infty }left(f(x)-kxright)=lim _{xto +infty }{frac {b}{a}}left({sqrt {x^{2}-a^{2}}}-xright)=lim _{xto +infty }{frac {b}{a}}cdot {frac {a^{2}}{{sqrt {x^{2}-a^{2}}}+x}}=0.}$

Таким образом, уравнения двух асимптот имеют вид:

${displaystyle y=pm {frac {b}{a}}x}$

или

${displaystyle {frac {x}{a}}pm {frac {y}{b}}=0.}$

Диаметры и хорды[править | править код]

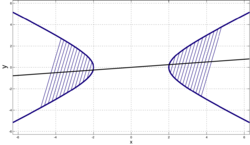
Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент $k_{1}$ соответствующего диаметра связан соотношением

${displaystyle kcdot k_{1}=varepsilon ^{2}-1={frac {b^{2}}{a^{2}}}.}$

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы

Касательная и нормаль[править | править код]

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}=1$

или, что то же самое,

$y=y_{0}+{frac {b^{2}x_{0}}{a^{2}y_{0}}}left(x-x_{0}right)$

Вывод уравнения касательной
Уравнение касательной произвольной плоской линии имеет вид $y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$ Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение касательной, получим $y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$ ${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Вывод уравнения касательной

Уравнение касательной произвольной плоской линии имеет вид

$y-y_{0}=y'left(x_{0},y_{0}right)cdot left(x-x_{0}right)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение касательной, получим

$y-y_{0}={frac {b^{2}}{a^{2}}}{frac {x_{0}}{y_{0}}}left(x-x_{0}right)$

${frac {xx_{0}}{a^{2}}}-{frac {yy_{0}}{b^{2}}}={frac {x_{0}^{2}}{a^{2}}}-{frac {y_{0}^{2}}{b^{2}}}=1$

Уравнение нормали к гиперболе имеет вид:

$y=y_{0}-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Вывод уравнения нормали
Уравнение нормали произвольной плоской линии имеет вид $y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$ . Каноническое уравнение гиперболы можно представить в виде пары функций $y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$ . Тогда производная этих функций имеет вид $y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$ . Подставив это уравнение в общее уравнение нормали, получим $y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$ .

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид

$y-y_{0}={frac {1}{y'left(x_{0},y_{0}right)}}left(x_{0}-xright)$

Каноническое уравнение гиперболы можно представить в виде пары функций

$y=pm {sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}$

Тогда производная этих функций имеет вид

$y'=pm {frac {{frac {b^{2}}{a^{2}}}x}{{sqrt {{frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}}={frac {b^{2}}{a^{2}}}{frac {x}{y}}$

Подставив это уравнение в общее уравнение нормали, получим

$y-y_{0}=-{frac {a^{2}}{b^{2}}}{frac {y_{0}}{x_{0}}}left(x-x_{0}right)$

Кривизна и эволюта[править | править код]

Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

$K={frac {ab}{left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}}$

Соответственно, радиус кривизны имеет вид:

$R={frac 1K}={frac {left({frac {a^{2}}{b^{2}}}y^{2}+{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

В частности, в точке (a, 0) радиус кривизны равен

$Rleft(a,0right)={frac {b^{2}}{a}}=p$

Вывод формулы для радиуса кривизны
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид: $R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left\|x'y''-x''y'right\|}}$ . Воспользуемся параметрическим представлением гиперболы: ${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$ Тогда, первая производная x и y по t имеет вид ${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$ , а вторая производная – ${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$ Подставляя эти значения в формулу для кривизны получаем: $R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left\|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft\|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right\|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$ .

Вывод формулы для радиуса кривизны

Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:

$R_{c}={frac {left(x'^{2} +y'^{2}right)^{{3/2}}}{left|x'y''-x''y'right|}}$

Воспользуемся параметрическим представлением гиперболы:

${begin{cases}x=acdot {mathrm {ch}},(t)\y=bcdot {mathrm {sh}},(t)end{cases}}$

Тогда, первая производная x и y по t имеет вид

${begin{cases}x'=acdot {mathrm {sh}},(t)={frac {a}{b}}y\y'=bcdot {mathrm {ch}},(t)={frac {b}{a}}xend{cases}}$

а вторая производная –

${begin{cases}x''=acdot {mathrm {ch}},(t)=x\y''=bcdot {mathrm {sh}},(t)=yend{cases}}$

Подставляя эти значения в формулу для кривизны получаем:

$R_{c}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{left|a{frac {y^{2}}{b}}-b{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ableft|{frac {y^{2}}{b}}-{frac {x^{2}}{a}}right|}}={frac {left({frac {a^{2}}{b^{2}}}y^{2} +{frac {b^{2}}{a^{2}}}x^{2}right)^{{3/2}}}{ab}}$

Координаты центров кривизны задаются парой уравнений:

${begin{cases}x_{c}={frac {x^{3}}{a^{2}}}left(1+{frac {b^{2}}{a^{2}}}right)\y_{c}=-{frac {y^{3}}{b^{2}}}left(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.

${begin{cases}x=pm a,{mathrm {ch}}^{3},tleft(1+{frac {b^{2}}{a^{2}}}right)\y=b,{mathrm {sh}}^{3},tleft(1+{frac {a^{2}}{b^{2}}}right)end{cases}}$

Эллиптическая система координат

Обобщение[править | править код]

Гипербола есть синусоидальная спираль при .

Применение[править | править код]

Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумерную эллиптическую систему координат.

Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.

Инверсией гиперболы с центром, лежащим в её собственном центре, в фокусе или на вершине можно получить соответственно лемнискату Бернулли, улитку Паскаля или строфоиду.

Гиперболы можно видеть на многих солнечных часах. В течение любого дня года Солнце описывает окружность на небесной сфере, и его лучи, падающие на верхушку гномона солнечных часов, описывают конус света. Линия пересечения этого конуса с плоскостью горизонтальных или вертикальных солнечных часов является коническим сечением. На наиболее населённых широтах и в большую часть года это коническое сечение является гиперболой. На солнечных часах часто показаны линии, описываемые тенью от верхушки гномона в течение дня для нескольких дней года (например, дней летнего и зимнего солнцестояний), таким образом, на них часто можно видеть определённые гиперболы, вид которых различен для различных дней года и различных широт.

Гиперболы, соответствующие на плоскости траекториям первых межзвёздных объектов — 1I/Оумуамуа (зелёная линия) и 2I/Borisov (синия линия)

АМС, преодолевая притяжение основного влияющего на неё тела и далеко улетая от него, при отсутствии возмущений, должна двигаться по гиперболической траектории или параболической траектории, поскольку в таком случае теоретически возможно удаление до бесконечности от данного тела^[4]. В частности, гиперболическими относительно Солнца являются траектории АМС «Вояджер-1» и АМС «Вояджер-2», с эксцентриситетом 3,7 и 6,3 и большой полуосью 480,9 млн км и 601,1 млн км соответственно^[5]^[6]. Гиперболическая траектория небесного тела в Солнечной системе может указывать на его межзвёздное происхождение. В конце 2010-х годов были открыты первый межзвёздный астероид и первая межзвёздная комета^[7], их траектории — гиперболические. Однако известные ранее кометы с гиперболической траекторией небольшого эксцентриситета только собираются стать межзвёздными: испытав во время своей «жизни» в Солнечной системе возмущение от такой планеты, как Юпитер, они ложатся на межзвёздный курс^[8].

См. также[править | править код]

Гиперболоид
Гиперболы, описанные около треугольника
Каустика
Конические сечения
Кривая второго порядка
Окружность
Парабола
Эллипс
Кривая постоянной суммы расстояний между двумя точками — эллипс,
Кривая постоянной разности расстояний между двумя точками — гипербола,
Кривая постоянного отношения — окружность Аполлония,
Кривая постоянного произведения — овал Кассини.
Сглаженный восьмиугольник § Построение

Примечания[править | править код]

↑ Eddy, R. H. and Fritsch, R. The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Math. Mag. 67, pp. 188—205, 1994.
↑ Шнейдер В.Е. Краткий курс высшей математики. — Рипол Классик. — ISBN 9785458255349.
↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 15—16. — 288 с.
↑ Сихарулидзе Ю. Г. Баллистика летательных аппаратов. — М.: Наука, 1982. — С. 162—163. — 5750 экз.
↑ Voyager – Hyperbolic Orbital Elements. НАСА. Дата обращения: 29 октября 2019. Архивировано 6 мая 2021 года.
↑ Ulivi P., Harland D. M. Robotic Exploration of the Solar System. Part I: The Golden Age 1957-1982. — Springer, Praxis, 2007. — P. 441. — ISBN 978-0-387-49326-8. Содержит эксцентриситет орбиты АМС «Вояджер-2» относительно Солнца после пролёта Нептуна.
↑ Naming of New Interstellar Visitor: 2I/Borisov. МАС (24 сентября 2019). Дата обращения: 24 сентября 2019. Архивировано 23 апреля 2020 года.
↑ Carl Sagan, Ann Druyan. Comet. — New York: Ballantine Books, 1997. — P. 104. — ISBN 0-345-41222-2.

Литература[править | править код]

Бронштейн И. Гипербола // Квант. — 1975. — № 3.
Граве Д. А. Гиперболы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982.
Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — Вып. 4. Архивировано 14 сентября 2008 года.

Источник

Гипербола

Гиперболой называется
геометрическое место точек плоскости,
для каждой из которых абсолютная величина
разности расстояний до двух фиксированных
точек той же плоскости, называемых
фокусами гиперболы, есть величина
постоянная.

Так же, как и в случае эллипса, для
получения уравнения гиперболы выберем
подходящую систему координат. Начало
координат расположим на середине отрезка
между фокусами, ось
направим
вдоль этого отрезка, а ось ординат –
перпендикулярно к нему.

Пусть расстояние между фокусами

и

гиперболы равно
,
а абсолютная величина разности расстояний
от точки гиперболы до фокусов равна
.

– текущая точка гиперболы (рис. 5).

Рис.5.

Так как разность двух сторон треугольника
меньше третьей стороны, то
,
то есть
,

.
По условию, фокусы
,
.

По определению гиперболы

Это уравнение запишем в виде

Обе части возведем в квадрат:

После приведения подобных членов и
деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные
члены, получим

С учетом того, что

уравнение принимает вид

Разделим обе части уравнения на
и
получим уравнение
(4)

Уравнение (4) называется каноническим
уравнением гиперболы.

Гипербола обладает двумя взаимно
перпендикулярными осями симметрии, на
одной из которых лежат фокусы гиперболы,
и центром симметрии. Если гипербола
задана каноническим уравнением, то ее
осями симметрии служат координатные
оси Ox
и
,
а начало координат – центр симметрии
гиперболы.

Проведем построение гиперболы, заданной
уравнением (4). Заметим, что из-за симметрии
достаточно построить кривую только в
первом координатном угле. Выразим из
канонического уравнения y
как функцию х,
при условии, что
,

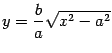
и построим график этой функции.

Область определения – интервал
,
,
функция монотонно растет. Производная

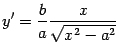
существует во всей области определения,
кроме точки. Следовательно, график –
гладкая кривая (без углов). Вторая
производная

во всех точках интервала

отрицательна, следовательно, график –
выпуклый вверх.

Проверим график на наличие асимптоты
при
.
Пусть асимптота имеет уравнение
.
Тогда по правилам математического
анализа

Выражение под знаком предела домножим
и разделим на
.
Получим

Итак, график функции имеет асимптоту

.
Из симметрии гиперболы следует, что

– тоже асимптота. (рис. 6).

Рис.6.График
функции

Окончательно, используя симметрию
гиперболы, получаем кривую рисунка 7.

Рис.6.Гипербола

Точки пересечения гиперболы, заданной
каноническим уравнением (4) с осью

называются
вершинами гиперболы, отрезок между
ними называется действительной осью
гиперболы. Отрезок оси ординат между
точками (0;-b) и (0; b)
называется мнимой осью. Числа
и

называются
соответственно действительной и
мнимой полуосями гиперболы. Начало
координат называется ее центром.
Величина

называется эксцентриситетом
гиперболы.

Из равенства

следует, что у гиперболы
.
Эксцентриситет
характеризует
угол между асимптотами, чем
ближе
к
1, тем меньше этот угол.????

Замечание
12.4 В отличие от эллипса в каноническом
уравнении гиперболы соотношение между
величинами
и

может
быть произвольным. В частности, при
мы
получим равностороннюю гиперболу,
известную из школьного курса математики.
Ее уравнение имеет знакомый вид
,
если взять
,
а оси
и

направить по биссектрисам четвертого
и первого координатных углов (рис. 7).

Рис.7.Равносторонняя
гипербола

Для отражения на рисунке качественных
характеристик гиперболы достаточно
определить ее вершины, нарисовать
асимптоты и нарисовать гладкую кривую,
проходящую через вершины, приближающуюся
к асимптотам и похожую на кривую рисунка
7.

Пример 2.4 Постройте гиперболу
,
найдите ее фокусы и эксцентриситет.

Решение. Разделим обе части уравнения
на 4. Получим каноническое уравнение

.
Проводим асимптоты

и строим гиперболу (рис. 8).

Рис.8.Гипербола

Из формулы

получим
.

Тогда фокусы –
,
,

Пример 12.5 Постройте гиперболу
.
Найдите ее фокусы и эксцентриситет.

Решение. Преобразуем уравнение к
виду

Данное уравнение не является каноническим
уравнением гиперболы, так как знаки
перед
и

противоположны знакам в каноническом
уравнении. Однако, если переобозначить
переменные
,

,
то в новых переменных получим каноническое
уравнение

Действительная ось этой гиперболы лежит
на оси
,
то есть на оси
исходной
системы координат, асимптоты имеют
уравнение
,
то есть уравнение

в исходных координатах. Действительная
полуось равна 5, мнимая — 2. В соответствии
с этими данными проводим построение
(рис. 12.14).

Рис.9.Гипербола
с уравнением

,
фокусы лежат на действительной оси –
,

,
где координаты указаны в исходной
системе координат.

Соседние файлы в папке модуль2

Источник

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если 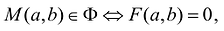, то есть (а, b) – решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

дано уравнение и надо построить фигуру Ф, уравнением которой является ;
дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 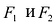, есть величина постоянная (большая, чем расстояние между ).

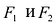Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с<а. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.

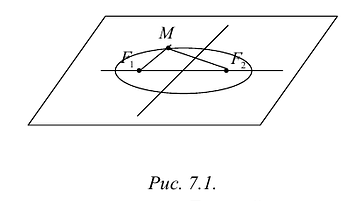
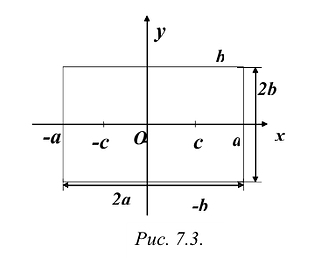
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами и с суммой расстояний от произвольной точки эллипса до фокусов, равной 2 а (Рис. 7.1).

Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы положительное направление оси – от , начало координат выберем в середине отрезка . Тогда координаты точек будут соответственно (-с,0) и (с,0).

Пусть М(х,у) – произвольная точка эллипса, тогда: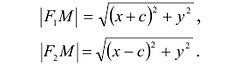

Подставляя сюда значения 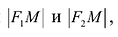имеем:

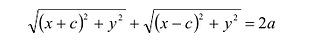(7.1)

Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим

его:

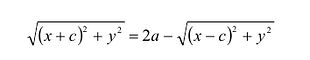
Возведя обе части уравнения в квадрат и приведя подобные члены, получим: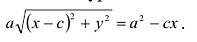

Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 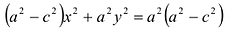или

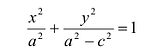(7.2)

Положительную величину 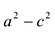обозначим через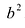. Тогда уравнение (7.2) примет вид:

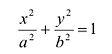(7.3)

Оно называется каноническим уравнение эллипса.

Координаты точек эллипса ограничены неравенствами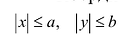. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 2а и 2b •

Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей Ох и Оу.

Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:

(7.4)

При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.

Рис. 7.4

Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).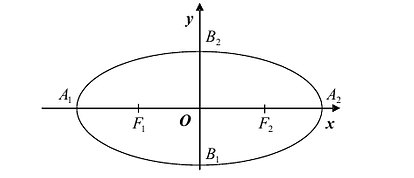

Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии – точка О – центром эллипса. Точки пересечения эллипса с осями координат называются вершинами эллипса. Отрезки 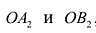, а также их длины а и Ь называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси Ох (как в нашем случае), из равенства 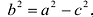следует, что a>b. В этом случае а называется большой полуосью, a b – малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

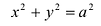(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 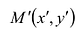координаты которой задаются формулами 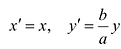будет окружность (4) переводить в эллипс, заданный соотношением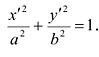

Число 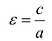называется эксцентриситетом эллипса. Эксцентриситет 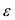характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 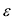становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 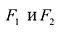. Их длины 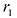и 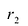задаются формулами 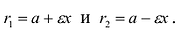Прямые 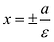называются директрисами эллипса. Директриса 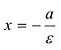называется левой, а 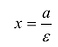– правой. Так как для эллипса 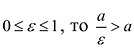и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.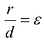

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).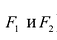

Точки 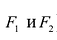называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 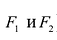обозначим через а. По условию, а <с.

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 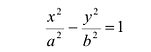(7.6) где ху – координаты произвольной точки гиперболы,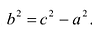

Уравнение (7.6) называется каноническим уравнением гиперболы.

Из уравнения (7.6) видно, что 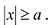. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми х = -а и х = а.

Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:

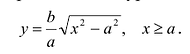
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:

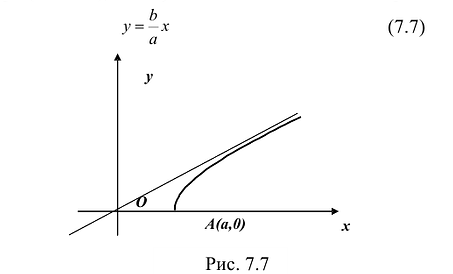
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты

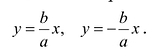
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).

Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки , пересечения гиперболы с осью Ох называются вершинами гиперболы. Величины а и Ь называются полуосями гиперболы. Если а=Ь, то гипербола называется равносторонней.

Эксцентриситетом гиперболы называется число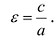. Для любой гиперболы 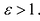. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси Ох. На рисунке 7.9 изображены гиперболы с различными значениями £.

Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами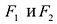. Их длины и 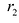задаются формулами:

Для правой – ветви ,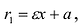

Для левой – ветви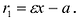

Прямые 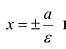называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением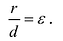

Парабола

Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой (директрисы).

Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом F и точкой D пересечения оси Ох с директрисой . Если обозначить через р расстояние фокуса от директрисы, то 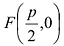и уравнение директрисы будет иметь вид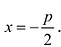

В выбранной системе координат уравнение параболы имеет вид:

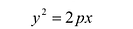(7.8)

Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .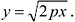

При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).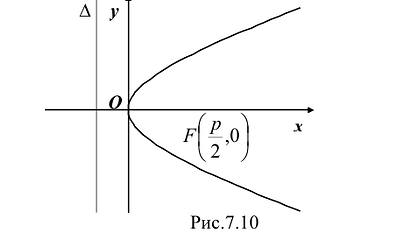

Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.

Исследование на плоскости уравнения второй степени

Рассмотрим уравнение:

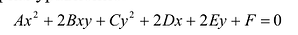(7.9)

где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно х и у.

Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол

Старые координаты х, у выражаются через новые координаты по формулам:

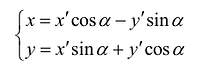(7.10)

Подставив выражения для х и у в уравнение (8), получим: 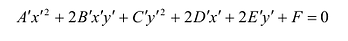(7.11)

Это уравнение в системе координат задает ту же линию, что и уравнение (7. 9) в системе Оху.

Если в уравнении (7.9) , то за счет выбора угла а в (7.10) можно добиться того, что В’ = 0. Для этого угол а надо взять таким, чтобы 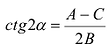. Поэтому будем считать В’= 0, тогда уравнение (7.11) примет вид:

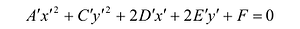(7.12)

Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:

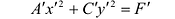(7.13)

В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Кривые второго порядка в высшей математике

Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.

Окружность

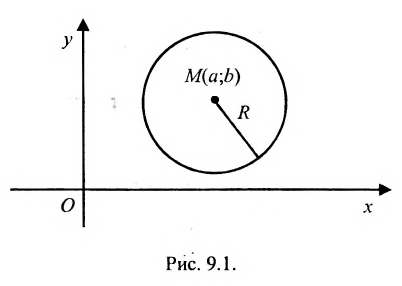
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки – центра окружности.

Если точка – центр (рис.9.1), N(x,y) – произвольная точка окружности и R – её радиус, то согласно определения можно записать

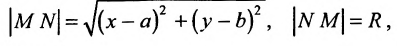
или

Найдём условия, при которых общее уравнение второй степени с двумя переменными

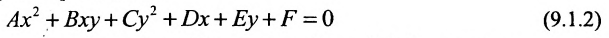
определяет окружность. Раскрыв скобки в (9.1.1), получим

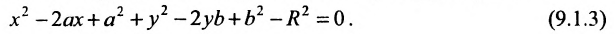
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,

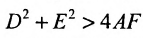, при выполнении которых общее уравнение (9.1.2) определяет окружность.

Эллипс

Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.

Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами и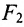. Пусть начало координат лежит на середине отрезка 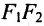. Выведем уравнение эллипса.

Если точка А – произвольная точка эллипса с координатами (х, у), то

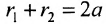(9.2.1)

где 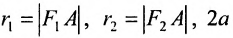– постоянная сумма. Так как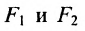

расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 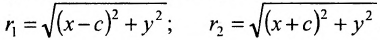. Подставив значения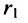

и 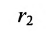в (9.2.1), получаем уравнение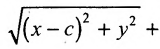

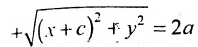
Обе части этого уравнения возведем в квад-Упростив и обозначив

получим. Разделим обе части уравнения на правую часть

Уравнение (9.2.2) называется каноническим уравнением эллипса, где а – большая полуось, b – малая полуось.

Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет 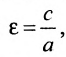, т.е. отношение расстояния между фокусами этого эллипса к длине его большей полуоси. Так как с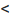а, то эксцентриситет каждого эллипса меньше единицы. Поскольку

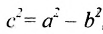, то подставив значение 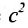в равенство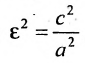, получим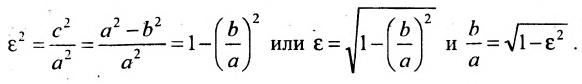

Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 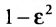, тем меньше, следовательно, отношение 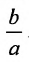. Это значит, что эллипс вытянут вдоль оси Ох. В случае Ь=а и 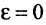получаем окружность.

Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 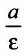от него, называются директрисами эллипса. Уравнения директрис

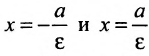
Пример:

Исследовать, какая линия определяется уравнением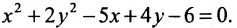

Решение:

Сгруппируем члены, содержащие одну и туже переменную, получим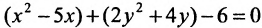

Из второй скобки вынесем коэффициент при 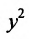, после чего предыдущее уравнение примет вид

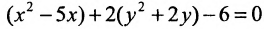
В каждой из скобок выделим полный квадрат

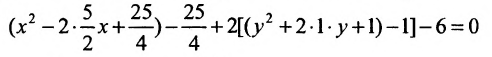
или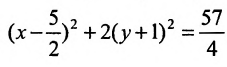

Произведём замену: 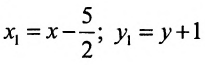. Исследуемое уравнение принимает вид: .

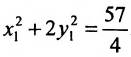Разделив обе части этого уравнения на 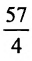, получим канонический вид данного уравнения: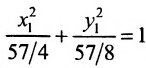

Заданное уравнение определяет эллипс с полуосями 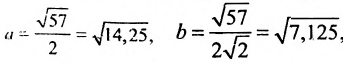, центр которого находится в точке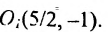

Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 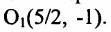. В новой системе координат строим основной прямоугольник со сторонами , стороны которого параллельны новым осям координат, а центр находится в точке . Вписываем в него эллипс.

Гипербола

Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).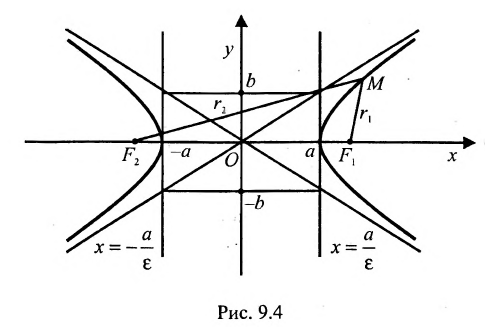

Пусть М- произвольная точка гиперболы с фокусами 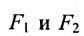(рис. 9.4). Отрезки 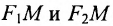называются фокальными радиусами точки М и обозначаются 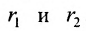По определению гиперболы 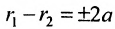. Так как 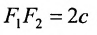и т.к. расположены симметрично относительно начала координат, то, применяя формулу для вычисления расстояния между двумя точками, находим 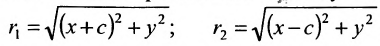. Заменяя в равенстве 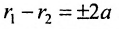найденными выражениями, получаем:

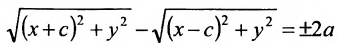Возведя в квадрат обе части этого уравнения и обозначая 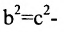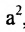, получим: 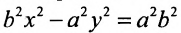или, разделив все члены уравнения на правую часть, приводим его к виду:

Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 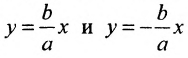. Поэтому, если требуется построить гиперболу с полуосями а и b, то следует, прежде всего, построить ее основной прямоугольник, затем асимптоты.

Уравнение вида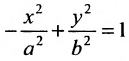 определяет гиперболу, вершины которой расположены на оси Оу (Рис. 9.5).

Форму гиперболы характеризует её эксцентриситет 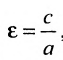, т.е. отношение расстояния между фокусами этой гиперболы к расстоянию между её вершинами. Поскольку 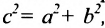, то подставив в формулу 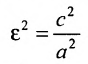получим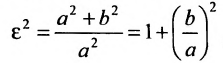откуда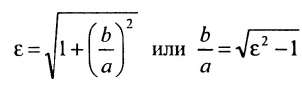. Следовательно, эксцентриситет oредсляется отношением 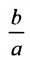, а отношение 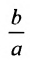– эксцентриситетом. Следовательно, эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем меньше отношение , а это значит, что основной прямоугольник вытянут в направлении оси, соединяющей вершины.

Прямые, заданные уравнениями 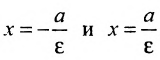называются директрисами гиперболы.

Пример:

Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.

Решение:

В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 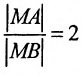.Подставив значения расстояний, которые находим по формуле расстояния между двумя точками, получим:

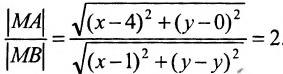
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:

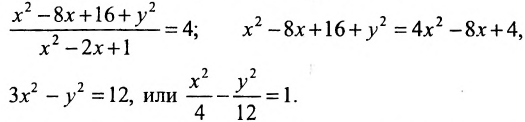
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая .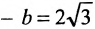

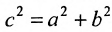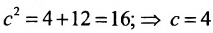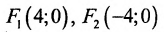Определим фокусы гиперболы. Для гиперболы выполняется равенство . Следовательно, .А – фокусы гиперболы. Как видно, заданная точка

А(4, 0) является правым фокусом гиперболы.

Эксцентриситет полученной гиперболы равен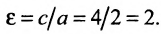

Подставив значения а и b в уравнения асимптот 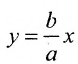и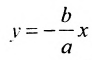

у =—получим уравнения асимптот гиперболы: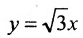и .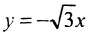

Для построения гиперболы строим основной прямоугольник с полуосями 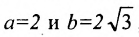, затеем асимптоты 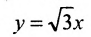и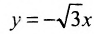 а далее строим и саму гиперболу (рис.9.6).

Заказать решение задач по высшей математике

Парабола

Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).

Обозначим фокус параболы – F, расстояние от фокуса до директрисы – р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 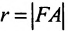. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

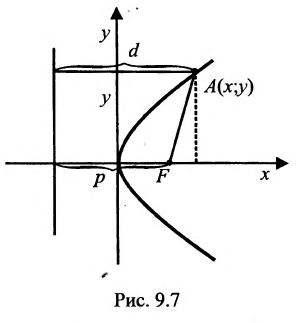
Тогда 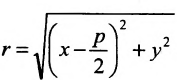А расстояние 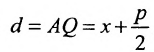Подставив в формулу r=d, будем иметь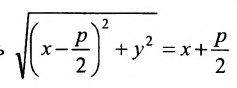. Возведя обе части равенства в квадрат, получим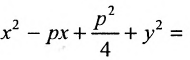

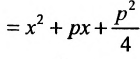или

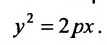(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 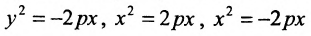также определяют параболы.

Легко показать, что уравнение 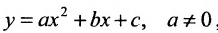, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 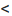О. Для этого выделим полный квадрат:

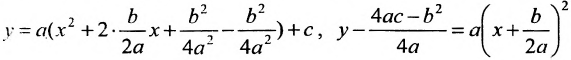
и сделаем параллельный перенос по формулам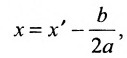

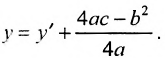
В новых координатах преобразуемое уравнение примет вид: 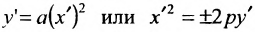где р – положительное число, определяется равенством .

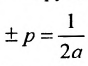Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию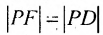, запишем это равенство с помощью координат: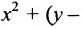 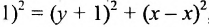, или после упрощения 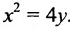. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

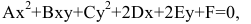
где коэффициенты А, В и С не равны одновременно нулю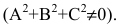

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.

Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и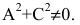

Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.

Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

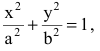которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число 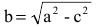– мень-

шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 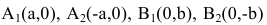называют вершинами эллипса, а 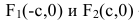– его фокусами (рис. 12).

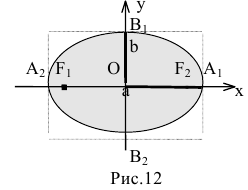
Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид 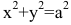и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

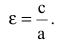
Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности 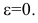Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

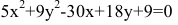
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

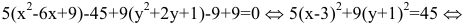
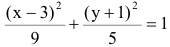– каноническое уравнение эллипса с центром в точке 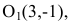большей полуосью а=3 и меньшей полуосью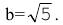

Найдем эксцентриситет эллипса:

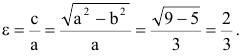
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 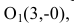а оси 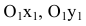параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.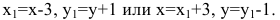

В новой системе координат координаты 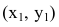вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

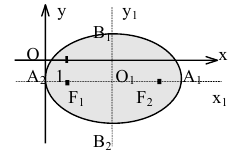Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению

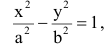которое называют каноническим уравнением гиперболы.

Число а называют действительной полуосью гиперболы, число

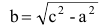– мнимой полуосью гиперболы, 2а и 2b – соответственно действительной и мнимой осями гиперболы. Точки 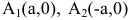называют вершинами гиперболы, 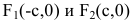– ее фокусами (рис. 13).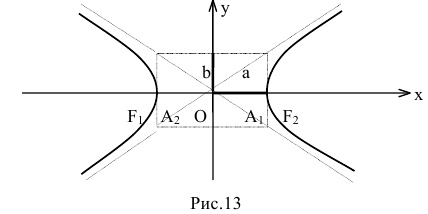

Координатные оси являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.

Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 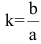), которые называются асимптотами гиперболы.

Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси: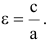

Эксцентриситет гиперболы изменяется от единицы до бесконечности 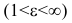и характеризует форму гиперболы. Чем меньше эксцентриситет гиперболы, тем ее ветви более сжаты к оси Ох.

Замечание. Каноническое уравнение 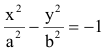определяет сопряженную гиперболу с действительной полуосью b, вершинами в точках 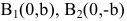и фокусами на оси Оу.

Пример:

Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.

Решение:

Каноническое уравнение гиперболы имеет вид

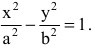По условию задачи нам известно: а=3, 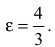Найдем мнимую полуось.

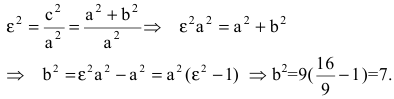
Следовательно, уравнение искомой гиперболы:

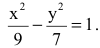Задача решена.

Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 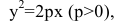которое называется каноническим уравнением параболы.

Точка O(0,0) называется вершиной параболы, число р – параметром параболы, 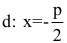– директрисой пир,болы, а 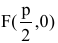– ее фокусом. Прямая у=0 является осью симметрии параболы, ветви которой направлены вправо. Центра симметрии у параболы нет (рис. 14).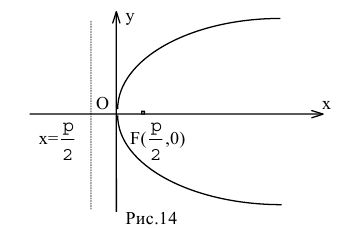

Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 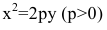(уравнение параболы с вертикальной осью, уравнением директрисы 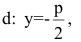фокусом 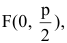ветви направлены вверх).

Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:

Пример:

Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной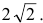

Решение:

Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:

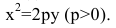
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений

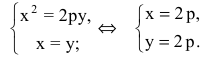
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной который является гипотенузой равнобедренного прямоугольного треугольника с катетами 2р.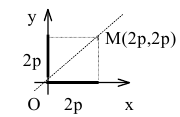

По теореме Пифагора

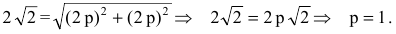
Тогда искомое уравнение параболы

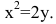
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).

Задача решена.

Евклидово пространство
Матрица – виды, операции и действия с примерами
Линейный оператор – свойства и определение
Многочлен – виды, определение с примерами
Числовые множества
Вектор – определение и основные понятия
Прямая – понятие, виды и её свойства
Плоскость – определение, виды и правила

Источник

Гипербола: формулы, примеры решения задач

Определение гиперболы, решаем задачи вместе

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

Гипербола – определение и вычисление с примерами решения

Гипербола в высшей математике

Как найти координаты фокусов гиперболы

Определение гиперболы, решаем задачи вместе

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

Гипербола: определение, свойства, построение

Фокальное свойство гиперболы

Директориальное свойство гиперболы

Уравнение гиперболы в полярной системе координат

Геометрический смысл коэффициентов в уравнении гиперболы

Параметрическое уравнение гиперболы

История[править | править код]

Определения[править | править код]

Коническое сечение[править | править код]

Как геометрическое место точек[править | править код]

Через фокусы[править | править код]

Через директрису и фокус[править | править код]

Связанные определения[править | править код]

Соотношения[править | править код]

Равнобочная гипербола[править | править код]

Гипербола Киперта[править | править код]

Уравнения[править | править код]

Декартовы координаты[править | править код]

Канонический вид[править | править код]

Полярные координаты[править | править код]

Уравнения в параметрической форме[править | править код]

Свойства[править | править код]

Асимптоты[править | править код]

Диаметры и хорды[править | править код]

Касательная и нормаль[править | править код]

Кривизна и эволюта[править | править код]

Обобщение[править | править код]

Применение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Гипербола

Эллипс

Гипербола

Парабола

Исследование на плоскости уравнения второй степени

Кривые второго порядка в высшей математике

Окружность

Эллипс

Гипербола

Парабола

Кривые второго порядка на плоскости

Вам также может понравиться

Как составить схему родства

Как найти слово во всех документах word

Как составить мотивированное мнение профсоюза образец

Добавить комментарий Отменить ответ