В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
-
Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
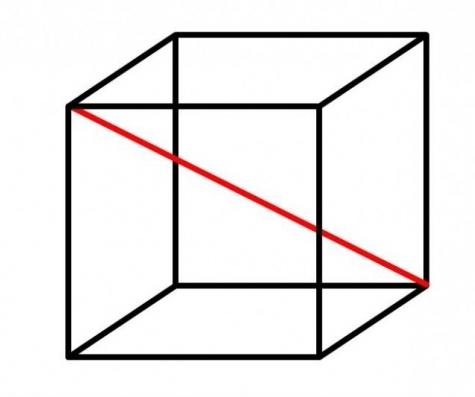
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Как найти диагональ грани куба
Если шесть граней квадратной формы ограничивают некоторый объем пространства, то геометрическую форму этого пространства можно назвать кубической или гексаэдрической. Все двенадцать ребер такой пространственной фигуры имеют одинаковую длину, что значительно упрощает вычисления параметров многогранника. Длина диагонали куба – не исключение, ее можно найти многими способами.

Инструкция
Если длина ребра куба (a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них и диагонали грани, является прямоугольным. Ребра в этом случае – катеты, а рассчитать вам нужно длину гипотенузы. Согласно упомянутой выше теореме она равна квадратному корню из суммы квадратов длин катетов, а так как в данном случае они имеют одинаковые размеры, просто умножьте длину ребра на квадратный корень из двойки: l = √(a²+a²) = √(2*a²) = a*√2.
Площадь квадрата тоже может быть выражена через длину диагонали, а так как каждая грань куба имеет именно такую форму, знания площади грани (s) достаточно для вычисления ее диагонали (l). Площадь каждой боковой поверхности куба равна возведенной в квадрат длине ребра, поэтому сторону квадрата грани можно выразить через нее как √s. Подставьте это значение в формулу из предыдущего шага: l = √s*√2 = √(2*s).
Куб составлен из шести граней одинаковой формы, поэтому, если в условиях задачи дана общая площадь поверхности (S), для вычисления диагонали грани (l) достаточно немного изменить формулу предыдущего шага. Замените в ней площадь одной грани одной шестой общей площади: l = √(2*S/6) = √(S/3).
Длину ребра куба можно выразить и через объем этой фигуры (V), а это позволяет формулу расчета длины диагонали грани (l) из первого шага использовать и в этом случае, внеся в нее некоторые поправки. Объем такого многогранника равен третей степени длины ребра, поэтому замените в формуле длину стороны грани кубическим корнем из объема: l = ³√V*√2.
Радиус описанной около куба сферы (R) связан с длиной ребра коэффициентом, равным половине корня из тройки. Выразите сторону грани через этот радиус и подставьте выражение во все ту же формулу вычисления длины диагонали грани из первого шага: l = R*2/√3*√2 = R*√8/√3.
Формула расчета диагонали грани (l) с использованием радиуса вписанной в куб сферы (r) будет еще проще, так как этот радиус составляет половину длины ребра: l = 2*r*√2 = r*√8.
Источники:
- диагональ куба
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
w2epadi8716
2020-05-17 14:47:14
найдите длину диагонали грани куба, если длина диагонали этого куба равна 4√3
математика 10-11 класс
2223
sova
2020-05-17 14:59:01
★
d^2=a^2+a^2+a^2
d^2=3a^2
(4sqrt(3))^2=3a^2
a^2=16
a=4
d^2_(грани)=a^2+a^2=4^2+4^2=32
[b]d_(грани)=4sqrt(2)[/b]
Что такое куб, и какие диагонали он имеет
Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба
Диаго
наль грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d – это диагональ квадрата, а – это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют прямоугольный треугольник. В этом трио диагональ играет роль гипотенузы, а стороны квадрата – это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Если известна площадь поверхности
Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см2. Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см2. Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a2, значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см2.
Если известна длина ребер куба
Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!
Диагональ грани куба Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина ребра куба: 10 метр –> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
14.142135623731 метр –> Конверсия не требуется
14 Диагональ грани куба Калькуляторы
7 Диагональ куба Калькуляторы
Диагональ грани куба формула
Диагональ грани куба = sqrt(2)*Длина ребра куба
dFace = sqrt(2)*le
Что такое куб?
Куб — это симметричная замкнутая трехмерная фигура, имеющая 6 одинаковых граней квадратной формы. У него 8 углов, 12 ребер и 6 граней. И каждый угол разделяется на 3 грани, а каждое ребро — на 2 грани Куба. Другими словами, прямоугольный ящик, в котором длина, ширина и высота численно равны, называется кубом. Это равное измерение называется длиной ребра куба. Также куб является платоновым телом.