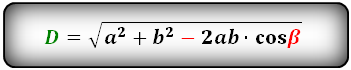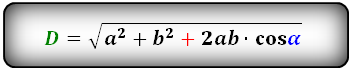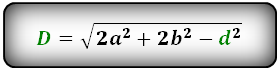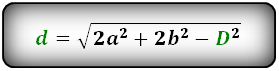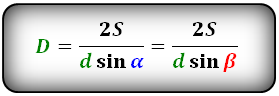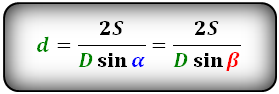Как найти длину диагонали параллелограмма по точкам

Задача 59148 Подскажите как правильно решать! Найти.

Условие

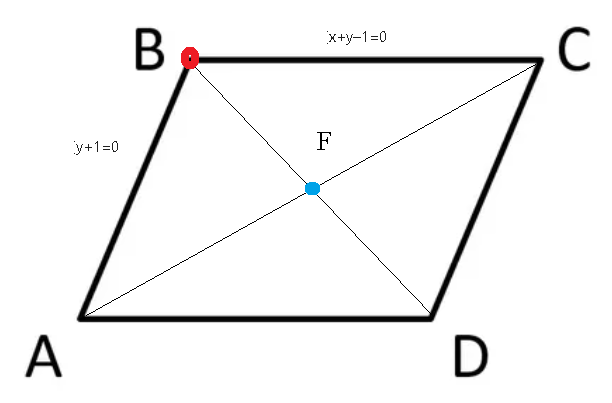
Подскажите как правильно решать! Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x+y-1=0 если у+1=0 если известно что диагональ параллелограмма пересекается в точке F(-1, 0) И надо ли в этой задаче чертить рисунок?

Решение

Можно нарисовать схематический чертеж, чтобы понять как решать задачу ( cм. рис)

Противоположные стороны параллелограмма параллельны.

Даны уравнения смежных сторон. Это может быть АВ и ВС

1) чтобы найти точку пересечения сторон АВ и ВС

Это и есть координаты точки B.

2)
Составить уравнение прямой, проходящей через две точки:
(2;-1) и F(–1, 0)

Это можно сделать двумя способами:

Уравнение прямой с угловым коэффициентом имеет вид:
y=kx+b

Подставляем координаты точек:
-1=k*2+b
0=k*(-1)+b
находим k и b

[b]x+3y+1=0[/b] – это ответ.

Второй способ
Уравнение прямой, проходящей через две точки имеет вид: ( cм. скрин)

Подставляем координаты точек

и получаем пропорцию:

[b]x+3y+1=0[/b]- ответ.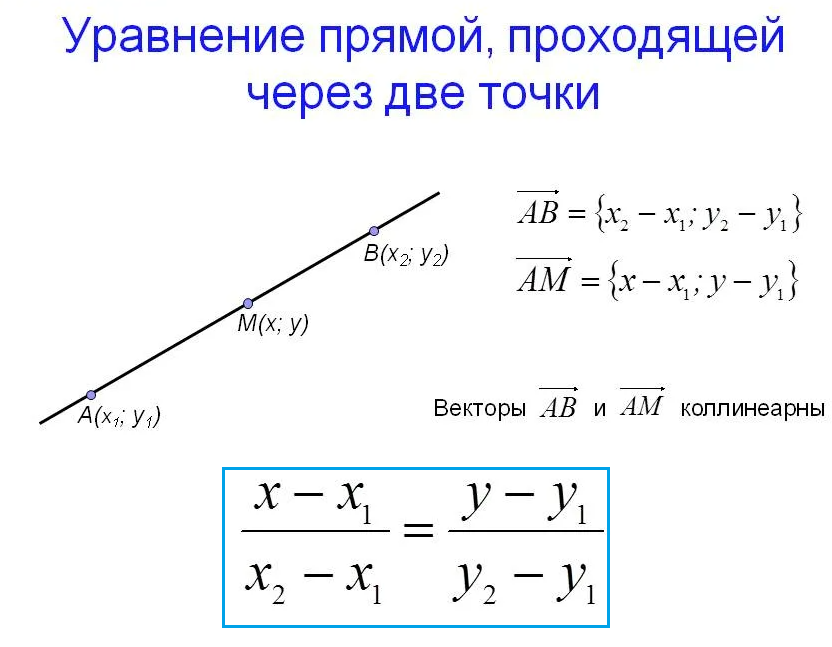

Диагонали параллелограмма

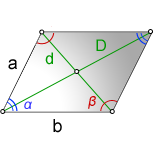
Нахождение диагоналей параллелограмма по двум сторонам и углу между ними.

Размышляя на тему Расчет векторов приложения сил обнаружил, что надо рассчитывать диагонали параллелограмма, да и углы не помешало бы находить.

На помощь приходит известная теорема косинусов:

и подробный рисунок:

после чего все становится ясно как день.

Итак, сначала используем теорему косинусов, чтобы найти короткую диагональ d1. Затем, тонко подмечая, что второй угол в параллелограмме равен 180 градусам минус первый, используем теорему косинусов, чтобы найти длинную диагональ d2. Зная диагонали, используем всё ту же теорему косинусов для нахождения оставшихся углов. И наконец, зная все углы между диагоналями и сторонами, находим углы между самими диагоналями, используя тот факт, что сумма углов треугольника равна 180. Найдя оба угла, выбираем меньший, его и выводим, так как второй, очевидно, 180 градусов минус первый.
Калькулятор ниже.

Параллелограмм. Формулы, признаки и свойства параллелограмма

Признаки параллелограмма

AB||CD, AB = CD (или BC||AD, BC = AD)

∠DAB = ∠BCD, ∠ABC = ∠CDA

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Основные свойства параллелограмма

∠ABC = ∠CDA, ∠BCD = ∠DAB

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:

AO = CO =	d 1
2
BO = DO =	d 2
2

AC 2 + BD 2 = 2AB 2 + 2BC 2

Стороны параллелограмма

Формулы определения длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и другую сторону:

a =	√ 2 d 1 2 + 2 d 2 2 – 4 b 2
2

b =	√ 2 d 1 2 + 2 d 2 2 – 4 a 2
2

3. Формула сторон параллелограмма через высоту и синус угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма

Формулы определения длины диагонали параллелограмма:

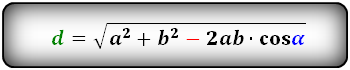
d ₁ = √ a 2 + b 2 – 2 ab·cosβ

d ₂ = √ a 2 + b 2 + 2 ab·cosβ

d ₁ = √ a 2 + b 2 + 2 ab·cosα

d ₂ = √ a 2 + b 2 – 2 ab·cosα

d ₁ = √ 2 a 2 + 2 b 2 – d ₂ 2

d ₂ = √ 2 a 2 + 2 b 2 – d ₁ 2

4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

d 1 =	2S	=	2S
d 2· sinγ	d 2· sinδ

d 2 =	2S	=	2S
d 1· sinγ	d 1· sinδ

Периметр параллелограмма

Формулы определения длины периметра параллелограмма:

P = 2 a + 2 b = 2( a + b )

P = 2 a + √ 2 d ₁ 2 + 2 d ₂ 2 – 4 a 2

P = 2 b + √ 2 d ₁ 2 + 2 d ₂ 2 – 4 b 2

3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

Площадь параллелограмма

Формулы определения площади параллелограмма:

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://planetcalc.ru/1149/

http://ru.onlinemschool.com/math/formula/parallelogram/

[/spoiler]

• 
  
  

Вычислите длины диагоналей параллелограмма ABCK, если известны координаты его вершин A(1; -3; 0), B(-2; 4; 1), C(-3; 1; 1).

Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра
взаимно параллельны.

В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос,
а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические
объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической
фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме
неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются
через расчет углы параллелограмма.

Длинная диагональ через две стороны и тупой угол

В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом
угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить
значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы
отнять это произведение и найти из этой разности квадратный корень.

D = √(a² + b² – 2 * a * b * cosβ

где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между
ребрами этой фигуры

Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120
градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 8) = 5,3
(ответ округлен)

Диагональ через две стороны и другую известную диагональ

В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую
диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем
сложить полученные значения (это первый результат). Потом следует возвести в квадрат значение длины
другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из
полученного значения квадратный корень.

D = √(2 * a² + 2 * b² – d²)

где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма

Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая
диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ
округленный)

Короткая диагональ через две стороны и тупой угол

Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре
через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются
полученные числа (один результат). Далее перемножаются значения длины ребер, косинус тупого угла,
удваивается полученное число (это другой результат). К одному результату прибавляется другой и
находится из полученного значения квадратный корень.

D = √(a² + b² + 2 * a * b * cosβ)

где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.

Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120)
между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6
(ответ округлен)

Длинная диагональ через две стороны и острый угол

В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем
расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести
в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое
слагаемое для последующего сложения). Затем умножаются длины ребер друг на друга, на косинус острого
угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из
суммы вычисляется квадратный корень.

D = √(a² + b² + 2 * a * b * cos α)

где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла

Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60
градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2
(округленно)

Короткая диагональ через две стороны и острый угол

В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и
острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные
значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла
между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть
второй и найти из полученного значения квадратный корень.

D = √(a² + b²– 2 * a * b * cosα)

где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами
параллелограмма

Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними
0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 8) = 3,5
(ответ округлен)

Диагональ через площадь, другую известную диагональ и угол между диагоналями

В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные
вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить
значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка,
соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем
следует разделить первый результат на второй.

D = (2 * S) / (d * sin α)

где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой
геометрической фигуры, sinα – синус угла между диагоналями параллелограмма

Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30
градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---