Как найти длину диагонали правильного многоугольника - Сайт, где вы сможете решить свои вопросы

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие:

Все стороны и углы одинаковы:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

α₁ = α₂ = α₃ = … = α_n-1 = α_n

Основные свойства правильного многоугольника

1. Все стороны равны:

a₁ = a₂ = a₃ = … = a_n-1 = a_n

2. Все углы равны:

α₁ = α₂ = α₃ = … = α_n-1 = α_n

3. Центр вписанной окружности O_в совпадает з центром описанной окружности O_о, что и образуют центр многоугольника O

4. Сумма всех углов n-угольника равна:

180° · (n – 2)

5. Сумма всех внешних углов n-угольника равна 360°:

β₁ + β₂ + β₃ + … + β_n-1 + β_n = 360°

6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Правильный n-угольник – формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

2. Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:

2. Формула площади n-угольника через радиус вписанной окружности:

3. Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

Изображение правильного треугольника с обозначениями

Рис.3

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:

4. Формула радиуса описанной окружности правильного треугольника через длину стороны:

5. Формула площади правильного треугольника через длину стороны:

6. Формула площади правильного треугольника через радиус вписанной окружности:

S = r² 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:

8. Угол между сторонами правильного треугольника:

α = 60°

Изображение правильного четырехугольнику с обозначениями

Рис.4

Правильный четырехугольник

Правильный четырехугольнику – квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

5. Формула площади правильного четырехугольника через длину стороны:

S = a²

6. Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r²

7. Формула площади правильного четырехугольника через радиус описанной окружности:

S = 2 R²

8. Угол между сторонами правильного четырехугольника:

α = 90°

Правильный шестиугольник

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:

2. Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

5. Формула площади правильного шестиугольника через длину стороны:

6. Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r² 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

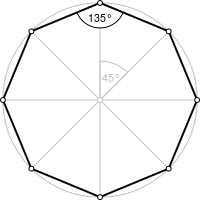
Правильный восьмиугольник

Формулы правильного восьмиугольника:

1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 – 1)

2. Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 – √2

3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

5. Формула площади правильного восьмиугольника через длину стороны:

S = a² 2(√2 + 1)

6. Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r² 8(√2 – 1)

7. Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R² 2√2

8. Угол между сторонами правильного восьмиугольника:

α = 135°

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a n-sided regular polygon of side length a.The task is to find the length of it’s diagonal.
Examples:

Input:  a = 9, n = 10
Output:  17.119

Input: a = 4, n = 5
Output: 6.47213

Approach:

We know that the sum of interior angles of a polygon = (n – 2) * 180 where, n is the no. of sides in the polygon.
So, each interior angle = (n – 2) * 180/n
Now, we have to find BC = 2 * x. If we draw a perpendicular AO on BC, we will see that the perpendicular bisects BC in BO and OC, as triangles AOB and AOC are congruent to each other.
Now, t = (n – 2) * 180/2n
So, sint = x/a
Therefore, x = asint
Hence, diagonal=2x = 2asint = 2asin((n – 2) * 180/2n)

C++

#include <bits/stdc++.h>

using namespace std;

float polydiagonal(float n, float a)

{

if (a < 0 && n < 0)

return -1;

return 2 * a * sin((((n - 2) * 180) / (2 * n)) * 3.14159 / 180);

}

int main()

{

float a = 9, n = 10;

cout << polydiagonal(n, a) << endl;

return 0;

}

Java

class GFG {

static float polydiagonal(float n, float a) {

if (a < 0 && n < 0) {

return -1;

}

return (float) (2 * a * Math.sin((((n - 2) * 180) / (2 * n)) * 3.14159 / 180));

}

public static void main(String[] args) {

float a = 9, n = 10;

System.out.printf("%.3f",polydiagonal(n, a));

}

Python3

import math as mt

def polydiagonal(n, a):

if (a < 0 and n < 0):

return -1

return (2 * a * mt.sin((((n - 2) * 180) /

(2 * n)) * 3.14159 / 180))

a, n = 9, 10

print(polydiagonal(n, a))

C#

using System;

public class GFG{

static float polydiagonal(float n, float a) {

if (a < 0 && n < 0) {

return -1;

}

return (float) (2 * a * Math.Sin((((n - 2) * 180) / (2 * n)) * 3.14159 / 180));

}

static public void Main (){

float a = 9, n = 10;

Console.WriteLine(polydiagonal(n, a));

}

PHP

<?php

function polydiagonal ($n, $a)

{

if ($a < 0 && $n < 0)

return -1;

return 2 * $a * sin(((($n - 2) * 180) /

(2 * $n)) * 3.14159 / 180);

}

$a = 9;

$n = 10;

echo polydiagonal($n, $a);

?>

Javascript

<script>

function polydiagonal(n , a) {

if (a < 0 && n < 0) {

return -1;

}

return (2 * a * Math.sin((((n - 2) * 180)

/ (2 * n)) * 3.14159 / 180));

}

var a = 9, n = 10;

document.write(polydiagonal(n, a).toFixed(3));

</script>

Time Complexity: O(1)

Auxiliary Space: O(1)

Last Updated :
23 Jun, 2022

Like Article

Save Article

Источник

Правильный многоугольник
Правильный восьмиугольник
Тип	Многоугольник
Символ Шлефли
Вид симметрии	Диэдрическая группа ${displaystyle (mathrm {D} _{5})}$
Площадь	${displaystyle S={frac {n}{4}} a^{2}operatorname {ctg} {frac {pi }{n}}}$
Внутренний угол	${displaystyle (n-2)*180^{circ }}$
Свойства
выпуклый, вписанный, равносторонний, равноугольный^[en], изотоксальный
Медиафайлы на Викискладе

Пра́вильный многоуго́льник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Связанные определения[править | править код]

Центром правильного многоугольника называется его центр масс, совпадающий с центрами его вписанной и описанной окружностей.

Свойства[править | править код]

Координаты[править | править код]

Пусть $x_{C}$ и $y_{C}$ — координаты центра, а — радиус описанной вокруг правильного многоугольника окружности, ${phi }_{0}$ — угловая координата первой вершины относительно центра, тогда декартовы координаты вершин правильного n-угольника определяются формулами:

$x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)$

$y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)$

где принимает значения от до n-1 .

Размеры[править | править код]

Правильный многоугольник, вписанный и описанный около окружности

Пусть — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен

$r=Rcos {frac {pi }{n}}$

а длина стороны многоугольника равна

$a=2Rsin {frac {pi }{n}}=2r{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь[править | править код]

Площадь правильного многоугольника с числом сторон и длиной стороны составляет:

$S={frac {n}{4}} a^{2}{mathop {{mathrm {}}}},operatorname {ctg}{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон , вписанного в окружность радиуса , составляет:

$S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}$

Площадь правильного многоугольника с числом сторон , описанного вокруг окружности радиуса , составляет:

$S=nr^{2}{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон равна

${displaystyle S={frac {nra}{2}}={frac {1}{2}}Pr}$

где — радиус вписанной окружности многоугольника, — длина его стороны, а – его периметр.

Периметр[править | править код]

Если нужно вычислить длину стороны a_n правильного n-угольника, вписанного в окружность, зная длину окружности можно вычислить длину одной стороны многоугольника:

— длина стороны правильного n-угольника.

${displaystyle a_{n}=sin {Big (}{frac {pi }{n}}{Big )}cdot {frac {L}{pi }}}$

Периметр $P_{n}$ равен

$P_{n}=a_{n}cdot n$

где — число сторон многоугольника.

Свойства диагоналей правильных многоугольников[править | править код]

Максимальное количество диагоналей правильного -угольника, пересекающихся в одной точке, не являющейся его вершиной или центром, равно:

Существуют лишь три исключения: данное число равно

в треугольнике,

в шестиугольнике и

в двенадцатиугольнике.^[3].

При чётном

в центре многоугольника пересекается n/2

диагонали.

Введём функцию ${displaystyle delta _{m}(n)}$ , равную в случае, если делится на , и равную в противном случае. Тогда:

Количество точек пересечения диагоналей правильного -угольника равно

${displaystyle {begin{array}{l}C_{n}^{4}+left(-5n^{3}+45n^{2}-70n+24right)/24cdot delta _{2}(n)-(3n/2)cdot delta _{4}(n)+\+left(-45n^{2}+262nright)/6cdot delta _{6}(n)+42ncdot delta _{12}(n)+60ncdot delta _{18}(n)+\+35ncdot delta _{24}(n)-38ncdot delta _{30}(n)-82ncdot delta _{42}(n)-330ncdot delta _{60}(n)-\-144ncdot delta _{84}(n)-96ncdot delta _{90}(n)-144ncdot delta _{120}(n)-96ncdot delta _{210}(n)end{array}}}$

Где ${displaystyle C_{n}^{4}}$

– число сочетаний из

по

^[3].

Количество частей, на которые правильный -угольник делят его диагонали, равно

${displaystyle {begin{array}{l}left(n^{4}-6n^{3}+23n^{2}-42n+24right)/24+\+left(-5n^{3}+42n^{2}-40n-48right)/48cdot delta _{2}(n)-(3n/4)cdot delta _{4}(n)+\+left(-53n^{2}+310nright)/12cdot delta _{6}(n)+(49n/2)cdot delta _{12}(n)+32ncdot delta _{18}(n)+\+19ncdot delta _{24}(n)-36ncdot delta _{30}(n)-50ncdot delta _{42}(n)-190ncdot delta _{60}(n)-\-78ncdot delta _{84}(n)-48ncdot delta _{90}(n)-78ncdot delta _{120}(n)-48ncdot delta _{210}(n)end{array}}}$

^[3].

Применение[править | править код]

Правильными многоугольниками по определению являются грани правильных многогранников.

Древнегреческие математики (Антифонт, Брисон Гераклейский, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.^[4]

История[править | править код]

Построение циркулем и линейкой правильного многоугольника с сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на равных частей, так как, соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.

Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для . Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с $2^{m}$ сторонами (при целом m>1 ), имея уже построенный многоугольник с числом сторон ${displaystyle 2^{m-1}}$ : пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат, потом правильный восьмиугольник, правильный шестнадцатиугольник и так далее. Кроме этого, в той же книге Евклид указывает и второй критерий построимости: если известно, как строить многоугольники с и сторонами, и и взаимно простые, то можно построить и многоугольник с сторонами. Это достигается построением многоугольника с сторонами и многоугольника с сторонами так, чтобы они были вписаны в одну окружность и чтобы одна вершина у них была общей – в таком случае некоторые две вершины этих многоугольников будут являться соседними вершинами -угольника. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с ${displaystyle 2^{m}cdot 3}$ , ${displaystyle 2^{m}cdot 5}$ и ${displaystyle 2^{m}cdot 3cdot 5}$ сторонами при любом целом неотрицательном .

Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: . Вопрос о наличии или отсутствии других таких чисел остаётся открытым. Гаусс, в частности, первым смог доказать возможность построения правильного -угольника, а под конец жизни завещал выбить его на своём надгробии, однако скульптор отказался выполнять столь сложную работу.^[5]

Из результата Гаусса мгновенно следовало, что правильный многоугольник возможно построить, если число его сторон равно ${displaystyle 2^{k}{p_{1}}{p_{2}}cdots {p_{s}}}$ , где {k} — целое неотрицательное число, а ${p_{j}}$ — попарно различные простые числа Ферма. Гаусс подозревал, что это условие является не только достаточным, но и необходимым, но впервые это было доказано Пьером-Лораном Ванцелем в 1836 году. Итоговая теорема, совмещающая оба результата, называется Теоремой Гаусса-Ванцеля.

Последними результатами в области построения правильных многоугольников являются явные построения 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.

См. также[править | править код]

Правильный многогранник

Примечания[править | править код]

↑ МАТВОКС
↑ treugolniki.ru. Дата обращения: 12 мая 2020. Архивировано 2 июля 2020 года.
↑ ¹ ² ³ Bjorn Poonen and Michael Rubinstein “The number of intersection points made by thediagonals of a regular polygon”. Дата обращения: 16 июля 2020. Архивировано 17 июля 2020 года.
↑ А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5.
↑ Лабуда

Источник

Как посчитать диагональ

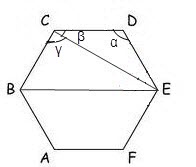
В геометрии существует несколько видов диагоналей. Диагональю называется отрезок, который соединяет две не соседние (не принадлежащие одной стороне или одному ребру) вершины многоугольника или многогранника. Различают так же диагонали граней, рассматриваемых как многоугольники и пространственные диагонали, соединяющие вершины разных граней многогранника. Существуют фигуры, у которых все диагонали равны между собой. На плоскости это правильный пятиугольник и квадрат, в пространстве – правильный октаэдр.Зная длины сторон правильного многоугольника или длины рёбер правильного многогранника можно вычислить длину любой диагонали.

Инструкция

В любом правильном многоугольнике углы равны между собой и вычисляются по формуле
?? = (N – 2) * 180?/N, где ?? – любой из углов правильного многоугольника, N – число вершин.
Зная углы при вершинах многоугольника, его диагонали можно вычислить, используя теорему косинусов
BE = v(AB? + AE? – 2 * AB * AE * cos??)

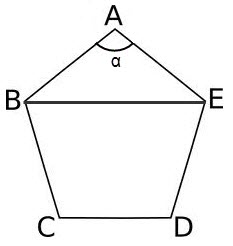
Если количество вершин больше пяти, то для вычисления диагоналей, которые соединяют вершины, лежащие на разных сторонах можно воспользоваться той же теоремой косинусов для вычисления углов образующихся треугольников. Например, в шестиугольнике ABCDEF, для нахождения диагонали BE, необходимо вычислить диагональ CE, затем по той же теореме косинусов вычислить угол ??, тогда ?? = ?? – ??. Таким образом,
BE = v(BC? + CE? – 2 * BC * CE * cos??).

Видео по теме

Обратите внимание

Для вычисления пространственной диагонали многогранника, необходимо построить сечение, содержащее эту диагональ, вычислить углы при вершинах этого сечения, рассматривая сечение как плоский многоугольник. Тогда диагональ можно рассчитать по приведённой выше схеме.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Содержание

Определение правильного многоугольника
Элементы правильного многоугольника
Диагонали n — угольника
Внешний угол многоугольника
Сумма внутренних углов
Сумма внешних углов
Виды правильных многоугольников
Основные свойства правильного многоугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Доказательства свойств углов многоугольника
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса описанной окружности правильного n-угольника
Формулы площади правильного n-угольника
Формула периметра правильного многоугольника:
Формула определения угла между сторонами правильного многоугольника:
Формулы правильного треугольника:
Формулы правильного четырехугольника:
Формулы правильного шестиугольника:
Формулы правильного восьмиугольника:
Сторона правильного многоугольника через радиус описанной вокруг него окружности
Шаг 1
Шаг 2
Шаг 3

Определение правильного многоугольника

Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.

Признаки правильного n-угольника

a1 = a2 = a3 = … an-1 = an
α1 = α2 = α3 = … αn-1 = αn

Примечание: n – количество сторон/углов фигуры.

Элементы правильного многоугольника

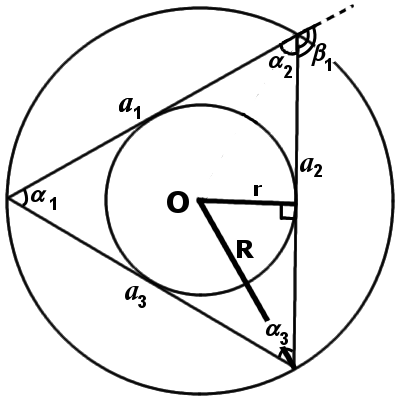
Для рисунка выше:

a – сторона/ребро;
α – угол между смежными сторонами;
O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
β – центральный угол описанной окружности, опирающийся на сторону многоугольника.

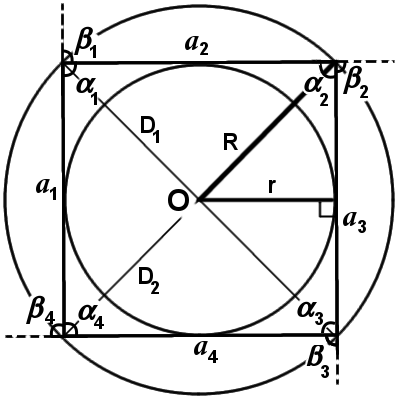
Диагонали n — угольника

Фигура	Рисунок	Описание
Диагональ многоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника		Число диагоналейn – угольника равно

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Внешний угол многоугольника

Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).

Рис.2

Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.

s = 2d(n — 2),

где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.

Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).

s = 4d,

где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Виды правильных многоугольников

Правильный (равносторонний) треугольник
Правильный четырехугольник (квадрат)
Правильный пяти-, шести-, n-угольник

Основные свойства правильного многоугольника

Все стороны равны:
a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:

180° · (n — 2)

Сумма всех внешних углов n-угольника равна 360°:

β1 + β2 + β3 + … + βn-1 + βn = 360°

Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Свойство 1

Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:

где n – число сторон фигуры.

Свойство 2

Сумма всех углов правильного n-угольника равняется: 180° · (n-2).

Свойство 3

Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:

Свойство 4

В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.

В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.

Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:

Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:

Свойство 5

Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:

Площадь (S):

Периметр (P):
Радиус описанной окружности (R):

Радиус вписанной окружности (r):

Свойство 6

Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:

Доказательства свойств углов многоугольника

Теорема 1. В любом треугольнике сумма углов равна 180°.

Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).

Рис.3

Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.

Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).

Рис.4

Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.

Замечание. Теорема 1 является следствием теоремы 2.

Теорема 3. Сумма углов – угольникаn равна

Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).

Рис.5

Получим n треугольников:

OA1A2, OA2A3, … OAnA1

Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна

что и требовалось доказать.

Теорема 4. Сумма внешних углов – угольникаn , взятых по одному у каждой вершины, равна 360°.

Доказательство. Рассмотрим рисунок 6.

Рис.6

В соответствии рисунком 6 справедливы равенства

Теорема доказана.

Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности:

Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны:

Формула площади n-угольника через радиус вписанной окружности:

Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

Рис.3

Формулы правильного треугольника:

Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

Формула радиуса вписанной окружности правильного треугольника через длину стороны:

Формула радиуса описанной окружности правильного треугольника через длину стороны:

Формула площади правильного треугольника через длину стороны:

Формула площади правильного треугольника через радиус вписанной окружности:

S = r2 3√3

Формула площади правильного треугольника через радиус описанной окружности:

Угол между сторонами правильного треугольника:

α = 60°

Рис.4

Формулы правильного четырехугольника:

Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

Формула площади правильного четырехугольника через длину стороны:

S = a2

Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r2

Формула площади правильного четырехугольника через радиус описанной окружности:

S = 2 R2

Угол между сторонами правильного четырехугольника:

α = 90°

Формулы правильного шестиугольника:

Формула стороны правильного шестиугольника через радиус вписанной окружности:

Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

Формула площади правильного шестиугольника через длину стороны:

Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r2 2√3

Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

Формулы правильного восьмиугольника:

Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 — 1)

Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 — √2

Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

Формула площади правильного восьмиугольника через длину стороны:

S = a2 2(√2 + 1)

Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r2 8(√2 — 1)

Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R2 2√2

Угол между сторонами правильного восьмиугольника:

α = 135°

Сторона правильного многоугольника через радиус описанной вокруг него окружности

Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле

Где:

a – длина его стороны;

R – радиус описанной окружности;

n – число сторон многоугольника.

Формула стороны правильного многоугольника

Шаг 1

Рассмотрим правильный многоугольник А1А2А3…Аn.

Пусть его сторона будет равна a.

Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.

Вывод формулы стороны правильного многоугольника.

Шаг 2

Соединим точку О с его вершинами. А1А2А3…Аn.

Рассмотрим треугольник ОА1А2.

Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.

Проведем в треугольнике А1ОА2 высоту ОК.

Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:

Вывод формулы стороны правильного многоугольника.

Шаг 3

Рассмотрим треугольник А1КО.

Этот треугольник прямоугольный, так как ОК – высота по построению.

Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.

Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:

По свойству углов правильного многоугольника, каждый угол равен:

Тогда угол ОА1К будет равен:

Из определения косинуса угла получим:

Отсюда:

Подставим в формулу значения, полученные выше и на шаге 2:

Умножим обе части уравнения на 2:

Воспользуемся формулами приведения

Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:

Вывод формулы стороны правильного многоугольника.

Источник

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Признаки правильного многоугольника

Основные свойства правильного многоугольника

Правильный n-угольник – формулы

Формулы длины стороны правильного n-угольника

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса описанной окружности правильного n-угольника

Формулы площади правильного n-угольника

Формула периметра правильного многоугольника:

Формула определения угла между сторонами правильного многоугольника:

Правильный треугольник

Формулы правильного треугольника:

Правильный четырехугольник

Формулы правильного четырехугольника:

Правильный шестиугольник

Формулы правильного шестиугольника:

Правильный восьмиугольник

Формулы правильного восьмиугольника:

C++

Java

Python3

C#

PHP

Javascript

Связанные определения[править | править код]

Свойства[править | править код]

Координаты[править | править код]

Размеры[править | править код]

Площадь[править | править код]

Периметр[править | править код]

Свойства диагоналей правильных многоугольников[править | править код]

Применение[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

Как посчитать диагональ

Определение правильного многоугольника

Элементы правильного многоугольника

Диагонали n — угольника

Внешний угол многоугольника

Сумма внутренних углов

Сумма внешних углов

Виды правильных многоугольников

Основные свойства правильного многоугольника

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Свойство 6

Доказательства свойств углов многоугольника

Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса описанной окружности правильного n-угольника

Формулы площади правильного n-угольника

Формула периметра правильного многоугольника:

Формула определения угла между сторонами правильного многоугольника:

Формулы правильного треугольника:

Формулы правильного четырехугольника:

Формулы правильного шестиугольника:

Формулы правильного восьмиугольника:

Сторона правильного многоугольника через радиус описанной вокруг него окружности

Шаг 1

Шаг 2

Шаг 3

Вам также может понравиться

Как хоббит нашел кольцо всевластия

Как найти название монеты

Росреестр как найти границы участка

Добавить комментарий Отменить ответ