Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.
Присоединиться к ExamMe
ЕГЭ по Математике (профильный)
Найдите длину диагонали…
Задание:
Найдите длину диагонали прямоугольника, вершины которого имеют координаты $(2; 1), (2; 4), (6; 1), (6; 4)$.
Решение:
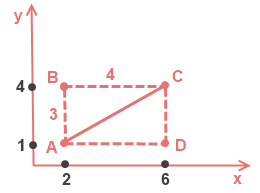
Для наглядности начертим и обозначим вершины этого прямоугольника (см. рисунок). А(2; 1), B(2; 4), D(6; 1), C(6; 4).
Найдем длину стороны $AB = 4-1 = 3$
Найдем длину стороны $BC = 6-2 = 4$
По теореме Пифагора вычислим диагональ AC.
[AC^2=AB^2+BC^2][AC=sqrt{3^2+4^2}][AC=sqrt{9+16}=sqrt{25}=5]
Ответ:
5
Задание добавил(а)
![]()
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
Задания
Версия для печати и копирования в MS Word
Задания Д6 № 513355 

Найдите длину диагонали прямоугольника, вершины которого имеют координаты (1; 2), (1; 10), (7; 2), (7; 10).
Спрятать решение
Решение.
Для того, чтобы найти диагональ прямоугольника, найдем длину и ширину
:
По теореме Пифагора: (диагональ d является гипотенузой)
Ответ: 10.
Аналоги к заданию № 513334: 513355 Все
Спрятать решение
·
Прототип задания
·
Помощь
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (3; 1), (11; 1), (11; 16), (3; 16).
Решение:
Изобразим прямоугольник на координатной плоскости:
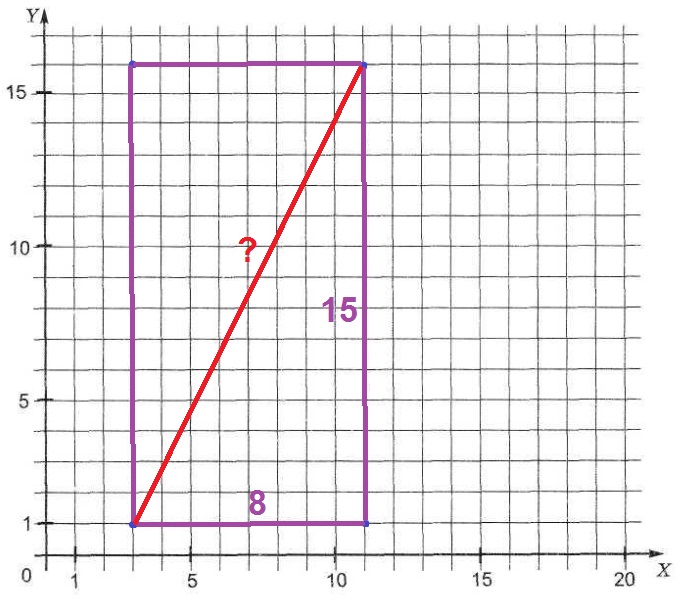
По рисунку видим, диагональ является гипотенузой прямоугольного треугольника со сторонами 8 и 15.
Найдём по теореме Пифагора диагональ:
d2 = 82 + 152 = 64 + 225 = 289
d = √289 = 17
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Найдем длину диагонали прямоугольника, вершины которого имеют координаты (2; 1), (2; 4), (6; 1), (6; 4).
Найдем стороны прямоугольника
Для этого, нужно найти расстояние между точками.
Пусть, а и b – стороны треугольника, где а – длина прямоугольника, b – ширина прямоугольника.
Расстояние между точками находиться по формуле √((x2 – x1) ^ 2 – (y2 – y1) ^ 2).
Для того, чтобы найти расстояние межу точками, нужно координаты точек подставить в формулу и вычислить значение выражения.
Сначала в порядке очереди вычисляем умножение или деление, потом проводятся действия сложения или вычитания. То есть получаем:
Расстояние между точками (2; 1) и (2; 4) равно:
а = √((x2 – x1) ^ 2 – (y2 – y1) ^ 2) = √((2 – 2) ^ 2 + (4 – 1) ^ 2) = √(0 ^ 2 + 3 ^ 2) = √(0 + 9) = √9 = 3 см;
Расстояние между точками (6; 1) и (6; 4) равно:
b = √((x2 – x1) ^ 2 – (y2 – y1) ^ 2) = √((6 – 6) ^ 2 + (4 – 1) ^ 2) = √(0 ^ 2 + 3 ^ 2) = √(0 + 9) = √9 = 3 см;
Отсюда получили, что a = b = 3 см.
Если все стороны равны, то прямоугольник является квадратом.
Найдем длину диагонали
Для того, чтобы найти длину диагонали, используем формулу d = √(a ^ 2 + b ^ 2), где:
- d – диагональ квадрата;
- а, b – стороны квадрата;
- a = b = 3 см.
Подставим известные значения в формулу длины диагонали, и вычислим его значение. То есть получаем:
d = √(a ^ 2 + b ^ 2) = √(3 ^ 2 + 3 ^ 2) = √(9 + 9) = √18 = √(9 * 2) = √9 * √2 = 3 * √2 см;
Отсюда получили, что диагональ равна d = 3 * √2 см.
Найдите длину диагонали прямоугольника, вершины которого
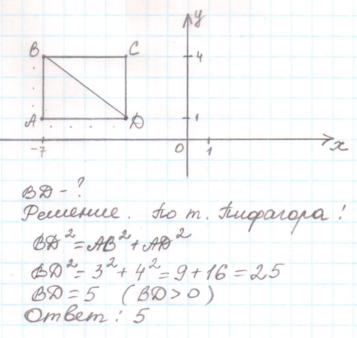
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (−7; 1), (−7; 4), (−3; 1), (−3; 4).
Решение: