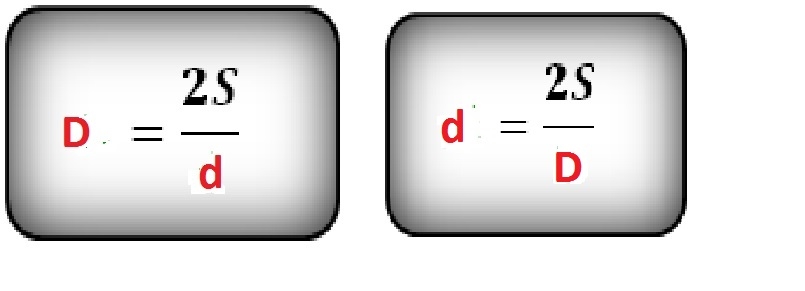Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.
- Диагональ ромба через сторону и другую известную
диагональ - Длинная диагональ ромба через сторону и острый угол
- Длинная диагональ ромба через сторону и тупой угол
- Короткая диагональ ромба через сторону и острый угол
- Короткая диагональ ромба через сторону и тупой угол
- Длинная диагональ ромба через короткую диагональ и тупой
угол - Короткая диагональ ромба через длинную диагональ и острый
угол - Диагональ ромба через площадь ромба и другую известную
диагональ
Диагональ ромба через сторону и другую известную диагональ
В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
d = √(4a² — d²)
где a — сторона, d — известная диагональ.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.
Как найти длину большей диагонали через сторону и острый угол
Найти величину длинной диагонали можно по формуле:
d = a * √(2 + 2 * cos α)
где a — сторона, cos α — острый угол.
Цифр после
запятой:
Результат в:
Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).
Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.
Как найти длину большей диагонали через сторону и известное значение тупого угла
Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:
d = a * √( 2 — 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.
Как вычислить длину меньшей диагонали через сторону и острый угол
Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.
d = a * √(2 — 2 * cos α)
где a — сторона, cos α — острый угол
Цифр после
запятой:
Результат в:
Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.
Короткая диагональ ромба через длинную диагональ и острый угол
Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:
d = D * tg (α / 2)
где D — длинная диагональ, α — острый угол
Цифр после
запятой:
Результат в:
Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.
Короткая диагональ через сторону и тупой угол
Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:
d = a * √(2 + 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 * √(2 + 2 * cos 128°) = 4 мм.
Длинная диагональ ромба через короткую диагональ и тупой угол
Длина большей диагонали ромба легко находится по формуле:
D = d * tg (β / 2)
где d — короткая диагональ, β — тупой угол
Цифр после
запятой:
Результат в:
Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.
Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.
Диагональ ромба через площадь и другую известную диагональ
Найти любую из двух диагоналей ромба можно по формуле:
D = 2 * S / d
где d – длина известного отрезка, а S-площадь фигуры.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.
Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:
- Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
всегда разделяют фигуру на 4 прямоугольных треугольника. - Противоположные стороны ромба попарно параллельны.
- Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
- Диагонали служат биссектрисами всех углов ромба.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
- Если соединить середины сторон ромба, получится прямоугольник.
- Точка пересечения диагоналей — центр вписанной окружности.
Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.
Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.
Fell
Профи
(936),
на голосовании
11 лет назад
Голосование за лучший ответ
Den Porsche
Мастер
(1408)
11 лет назад
ответ 6см
в ромбе все стороны равны
одна сторона следовательно равна 5 см
если разделить ромб диагоналями получаем 4 прямоугольных треугольника
каждый такой треугольник имеет гипотенузу 5 см и один катет 4см ( 8 / 2 )
находим второй катет из прямоугольного треугольника и умножаем его на 2 чтоб получить вторую диагональ ромба
Poli
Искусственный Интеллект
(155237)
11 лет назад
все ж поделено на треугольники, узнай сттороны и сумма 2 сторон треугольников
NaumenkoВысший разум (856084)
11 лет назад
много проще исходить из равных 4-х треугольников. на которые разбивают диагонали ромб. в которых известна гипотенуза 14Р и один из катетов – 12диагонали тоже заданной. картинка. конечно. красивая… только в этой задаче не нужна. вы “узнали” то, что задано. вот казус-то….ДИАГОНАЛЬ нужна.
Как найти диагональ ромба если известен периметр и угол.
На этой странице сайта размещен вопрос Как найти диагональ ромба если известен периметр и угол? из категории
Геометрия с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 1 – 4 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Как найти диагональ ромба
Ромб – четырехугольник, стороны которого равны и попарно параллельны. В отличие от квадрата, углы у которого прямые, ромб имеет по два острых и два тупых угла, лежащих на противоположных сторонах. А вот диагонали пересекаются под прямым углом и являются одновременно биссектрисами. Точка пересечения диагоналей делит их на равные части.
Формул для нахождения диагоналей ромба много, необходимо лишь знать исходные данные и подобрать подходящую.
1
Как найти диагональ ромба через сторону и угол: когда известны стороны и один из углов ромба, применяют следующие формулы:
2
Через сторону и половинный угол:
3
Через сторону и другую диагональ:
Сумма квадратов диагоналей равна квадрату стороны, умноженному на четыре D^2+d^2=4a^2. Отсюда можно вывести, что:
4
Через угол и другую диагональ:
5
Через площадь и другую диагональ: традиционной формулой для нахождения площади ромба считается S=a*h. Но относительно диагоналей она будет выглядеть S=1/2*D*d. После преобразований получаем:
6
Через периметр и другую диагональ. В этом случае формулу выведем самостоятельно. Т.к. ромб имеет равные стороны, чтобы найти одну из них, периметр делим на 4: a=P/4. Диагонали перпендикулярны друг другу и образуют прямой угол. Тогда одна из сторон и половины длин диагоналей образуют прямоугольный треугольник. Далее воспользуемся теоремой Пифагора. Для большой диагонали она будет выглядеть: D=2*(a^2-(d/2)^2)^1/2. Аналогично для нахождения малой диагонали: d=2*(a^2-(D/2)^2)^1/2.
Пример:
Найти меньшую диагональ ромба, если периметр равен 20 см, большая диагональ равна 8 см.
Дано: Р=20см, D=8 см. Найдем длину одной стороны ромба, разделив периметр на четыре a=20/4=5 см. Воспользуемся формулой пункта №3 и получим d=(4*5^2-8^2)^1/2=6 см.
Несмотря на кажущуюся простоту такой геометрической фигуры, как ромб, он таит в себе много интересных моментов. К нему применимы свойства параллелограмма, биссектрисы, прямоугольного, а иногда и равнобедренного треугольника. Зная формулы, легко можно решить задачи по нахождению диагоналей ромба.
Свойства ромба
- Противолежащие стороны ромба параллельны и равны.
- Диагонали ромба перпендикулярны.
- Точка пересечения диагоналей делит их пополам.
- Диагонали ромба являются биссектрисами его углов.
- Диагонали образуют из ромба 4 прямоугольных треугольника.
- Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.
- Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
Признаки ромба
- Параллелограмм с перпендикулярными диагоналями является ромбом.
-
Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то эта фигурой будет ромб.
Примечание: Не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом, так как прежде всего ромб это частный случай параллелограмма, а следовательно должен иметь все его признаки - Если в параллелограмм можно вписать круг, то он является ромбом
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
$$
AB = {S over AE}
$$
Длина стороны ромба через площадь (S) и синус угла
$$
AB = {sqrt{S} over sqrt{sin(∠CDA)}} = {sqrt{S} over sqrt{sin(∠DAB)}}
$$
Длина стороны ромба через диагонали
$$
AB = {sqrt{AC^2 + DB^2} over 2}
$$
Длина стороны ромба через диагональ и угол
$$
AB = {BD over 2 * cos(∠CDA)} = {AC over 2 * cos(∠DAB)}
$$
Длина стороны ромба через периметр
$$
AB = {P over 4}
$$
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$
BD = AB * sqrt{2 + 2 * cos(∠CDA)}
$$
$$
BD = AB * sqrt{2 – 2 * cos(∠DAB)}
$$
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$
AC = AB * sqrt{2 – 2 * cos(∠CDA)}
$$
$$
AC = AB * sqrt{2 + 2 * cos(∠DAB)}
$$
Длина диагонали ромба через сторону и другую диагональ
$$
BD = sqrt{4 * AB^2 + AC^2}
$$
$$
AC = sqrt{4 * AB^2 + BD^2}
$$
Длина диагонали ромба через площадь и другую диагональ
$$
BD = {2 * S over AC}
$$
$$
AC = {2 * S over BD}
$$
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
$$
BD = AC * tg({∠DAB over 2 })
$$
$$
AC = BD * tg({∠CDA over 2 })
$$
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
$$
S = AB * AE
$$
Площадь ромба через сторону и синус любого угла
$$
S = AB^2 * sin(∠CDA) = AB^2 * sin(∠DAB)
$$
Площадь ромба через две диагонали
$$
S = {1 over 2} * AC * BD
$$
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
$$
S = {1 over 2} * BD^2 * tg({∠CDA over 2})
$$
$$
S = {1 over 2} * AC^2 * tg({∠DAB over 2})
$$
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
$$
R = {AE over 2}
$$
Радиус вписанного круга в ромб через площадь и сторону ромба
$$
R = {S over 2 * AB}
$$
Радиус вписанного круга в ромб через сторону и синус любого угла
$$
R = {AB * sin(∠CDA) over 2} = {AB * sin(∠DAB) over 2}
$$
Радиус вписанного круга в ромб через диагональ и синус угла
$$
R = {BD * sin(∠CDA / 2) over 2}
$$
$$
R = {AC * sin(∠DAB / 2) over 2}
$$
Радиус вписанного круга в ромб через две диагонали
$$
R = {BD * AC over 2 * sqrt{BD^2 + AC^2}}
$$
Формулы высоты ромба
Высота ромба через сторону и угол
$$
AE = AB * sin(∠CDA) = AB * sin(∠DAB)
$$
Высота ромба через диагональ и угол
$$
AE = BD * sin({∠CDA over 2})
$$
$$
AE = AC * sin({∠DAB over 2})
$$
Высота ромба через диагонали
$$
AE = {BD * AC over sqrt{BD^2 + AC^2}}
$$
Высота ромба через диагонали и сторону
$$
AE = {BD * AC over 2 * AB}
$$
Формулы углов ромба
Косинус углов через диагональ и сторону
$$
cos(∠CDA) = {BD over 2 * AB^2} – 1 = 1 – {AC over 2 * AB^2}
$$
$$
cos(∠DAB) = {AC over 2 * AB^2} – 1 = 1 – {BD over 2 * AB^2}
$$
Синусы углов через диагонали
$$
sin(∠CDA) = sin(∠DAB) = {2 * BD * AC over BD^2 + AC^2}
$$
Синусы углов через площадь и сторону
$$
sin(∠CDA) = sin(∠DAB) = {S over AB^2}
$$
Тангенс половинных углов через диагонали
$$
tg(∠CDA) = {AC over BD}
$$
$$
tg(∠DAB) = {BD over AC}
$$