
{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.

-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
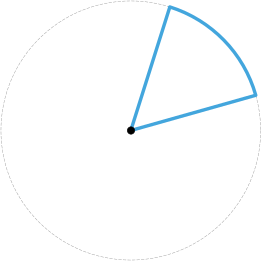
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
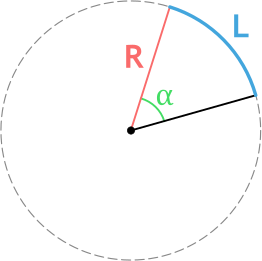
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
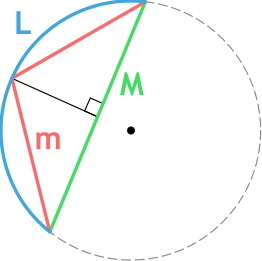
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Как найти длину дуги окружности ?
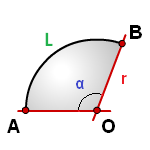
r– радиус окружности
α– угол AOB, в градусах
π ≈ 3.14
Формула длины дуги (L):

Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
- Подробности
-
Автор: Administrator
-
Опубликовано: 08 сентября 2011
-
Обновлено: 13 августа 2021
Определение окружности
Окружностью (см. Рис. 1) называется множество всех точек плоскости, которые равноудалены от одной точки (центра).

Рис. 1. Окружность
Длина дуги
Длина любой кривой (в том числе и дуги) приближённо описывается ломаной, вершины которой находятся на этой кривой. Если неограниченно измельчить звенья ломаной, то получим длину кривой (см. Рис. 2).

Рис. 2. Длина дуги окружности описывается ломаной
Длина окружности
Пусть дана окружность. Если изменить все радиусы данной окружности в ![]() раз, получим новую окружность, все размеры которой также изменятся в
раз, получим новую окружность, все размеры которой также изменятся в ![]() раз. Следовательно, отношение длины окружности к её диаметру будет числом постоянным:
раз. Следовательно, отношение длины окружности к её диаметру будет числом постоянным:
![]()
Такое отношение назвали числом пи (![]() ). Это число примерно равно 3,14.
). Это число примерно равно 3,14.
![]()
Выразим из этого выражения длину окружности (l):
![]() , где R – радиус окружности.
, где R – радиус окружности.
![]() – длина окружности
– длина окружности
Исходя из этой формулы, при ![]() :
:
![]() – длина единичной окружности
– длина единичной окружности
Необходимо ввести такую единицу измерения угла, чтобы полный угол был равен ![]() . Такой единицей измерения угла является радиан.
. Такой единицей измерения угла является радиан.
Определение радиана
Угол в один радиан – это такой центральный угол, длина дуги которого равна радиусу окружности (см. Рис. 3).
![]() ;
; ![]()

Рис. 3. Угол в один радиан
Связь между радианом и градусом
Формула длины окружности ![]() , следовательно, в одну окружность укладывается
, следовательно, в одну окружность укладывается ![]() радиусов (см. Рис. 4). Поэтому:
радиусов (см. Рис. 4). Поэтому:
![]()
![]()

Рис. 4. В одну окружность укладывается ![]() радиусов
радиусов
По полученной формуле можно переводить радианы в градусы или градусы в радианы. Например:
1. ![]()
2. ![]()
3. ![]()
Формула длины дуги окружности
Дано: ![]() ;
; ![]() (см. Рис. 5).
(см. Рис. 5).
Найти: ![]() .
.
Решение

Рис. 5. Длина дуги окружности
Дуга ![]() – это часть всей окружности. Длина окружности равна
– это часть всей окружности. Длина окружности равна ![]() , в окружности укладывается
, в окружности укладывается ![]() радиан, следовательно, длина дуги окружности, которая соответствует углу в один радиан, равна:
радиан, следовательно, длина дуги окружности, которая соответствует углу в один радиан, равна:
![]()
В ![]() всего
всего ![]() радиан, поэтому длина дуги окружности, соответствующая углу в
радиан, поэтому длина дуги окружности, соответствующая углу в ![]() радиан, равна:
радиан, равна:

Если ![]() , то:
, то:
![]()
Ответ: ![]() – формула длины дуги окружности.
– формула длины дуги окружности.
Задача 1
Дано: окружность радиуса ![]() (см. Рис. 6).
(см. Рис. 6).
Найти: 1. Длину дуги ![]() ; 2. Длину дуги
; 2. Длину дуги ![]() , если
, если ![]() .
.

Рис. 6. Иллюстрация к задаче
Решение
1. Так как окружность единичная, то её длина равна ![]() . Длина дуги
. Длина дуги ![]() составляет
составляет ![]() длины всей окружности. Поэтому её длина равна:
длины всей окружности. Поэтому её длина равна: ![]()
2. Длина дуги единичной окружности равна:
![]()
Поэтому:
![]()
Ответ: 1. ![]() ; 2.
; 2. ![]() .
.
Задача 2
Дано: окружность радиуса ![]() . Каждая четверть разделена пополам (см. Рис. 7).
. Каждая четверть разделена пополам (см. Рис. 7).
Найти: 1. ![]() ;
; ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() .
.

Рис. 7. Иллюстрация к задаче
Решение
Из предыдущей задачи известно, что длина четверти окружности равна ![]() . Следовательно:
. Следовательно:
1. ![]()
2. ![]()
3. ![]()
4. ![]() соответствует развёрнутому углу, то есть половина длины окружности, следовательно:
соответствует развёрнутому углу, то есть половина длины окружности, следовательно: ![]()
Ответ: 1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() .
.
Задача 3
Дано: окружность радиуса ![]() .
. ![]() (см. Рис. 8)
(см. Рис. 8)
Найти: 1. ![]() ;
; ![]() ; 2.
; 2. ![]() ;
; ![]() .
.

Рис. 8. Иллюстрация к задаче
Решение
1. Длина дуги ![]() равна
равна ![]() , следовательно:
, следовательно: ![]()
2. ![]()
![]()
Ответ: 1. ![]() ; 2.
; 2. ![]() ;
; ![]() .
.
Список литературы
1. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
2. Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
4. Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт aal100.narod.ru (Источник)
2. Интернет-сайт tvlad.ru (Источник)
Домашнее задание
1. Задание 11.3, 11.10, 11.13 (стр. 69–70) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)
2. Найдите радианные меры углов параллелограмма ABCD, если ![]() .
.
3. Найдите длину дуги окружности радиуса 1 см, отвечающей центральному углу: 1. 30°; 2. 45°; 3. 120°.
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить длину дуги сектора круга, а также разберем примеры решения задач для демонстрации их применения на практике.
- Определение дуги сектора круга
-
Формулы для нахождения длины дуги сектора
- Через центральный угол в градусах и радиус
- Через угол сектора в радианах и радиус
- Примеры задач
Определение дуги сектора круга
Дуга – это участок между двумя точками на окружности.
Дуга сектора круга – это участок между двумя точками на окружности, которые получены в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.
На рисунке ниже: AB – это дуга зеленого сектора круга с радиусом R (или r).

- OA = OB = R (r);
- α – угол сектора или центральный угол.
Формулы для нахождения длины дуги сектора
Через центральный угол в градусах и радиус
Длина (L) дуги сектора равняется числу π, умноженному на радиус круга (r), умноженному на центральный угол в градусах (α°), деленному на 180°.

Примечание: в расчетах используется число π, приблизительно равное 3,14.
Через угол сектора в радианах и радиус
Длина (L) дуги сектора равна произведению радиуса (r) и центрального угла, выраженного в радианах (aрад).
![]()
Примеры задач
Задание 1
Дан круг с радиусом 15 см. Найдите длину дуги сектора, угол которого равен 30°.
Решение
Воспользуемся формулой расчета, в которой используется центральный угол в градусах:
![]()
Задание 2
Длина дуги сектора равняется 24 см. Найдите, чему равен его угол (в радианах и градусах), если радиус круга составляет 12 см.
Решение
Для начала вычислим угол в радианах:
![]()
1 радиан ≈ 57,2958°
Следовательно, центральный угол приблизительно равняется 114,59° (2 рад ⋅ 57,2958°).
Урок “Длина дуги числовой окружности”
Краткое описание документа:
В 10 классе изучается числовая окружность. В содержание курса по данной теме входит урок «Длина дуги числовой окружности». Как и любой другой урок по математике, это занятие требует особых средств обучения, которые будут не только наглядными но и наиболее эффективными.
Данный урок длится 7: 11 минут. Примерно столько же времени требуется учителю, чтобы рассказать новый материал обучающимся. Но в этом случае учителю не придется перебирать множество литературы, пересматривать учебники в поиске самого главного по данной теме. Автор данного видеоурока позаботился о свободе учителя, собрал здесь самый свежий, полезный и главный материал.
Урок начинается с повторения формулы, по которой находится длина окружности. Но единичная окружность имеет радиус, равный 1, поэтому автор выводит для этого случая свою формулу, вычисляя, в конечном итоге, определенное значение длины числовой окружности. После этого вводится понятие длины дуги числовой окружности на примере единичной окружности.
После рассмотренной теории предлагается закрепить информацию с помощью примера. По условию необходимо найти длины дуг окружности, если в этой окружности проведены два взаимно перпендикулярных диаметра. При этом в задаче есть еще дополнительные сведения, которые помогут более точно найти искомую величину. Пример рассматривается с подробным объяснением решения. Здесь присутствует рисунок, иллюстрирующий суть задачи, математическая запись, развивающая математическую грамотность обучающихся, и логически построенное объяснение каждого этапа решения задачи.
Далее рассматривается не менее наглядный пример, где также необходимо найти длины дуг окружностей. Решение задачи имеет четкую структуру. Здесь имеется иллюстрация. Автор подробно поясняет все, что происходит на экране, все решение, и что, откуда берется.
После этого автор вводит проблему, которую постепенно приводит к решению. Рассказ автора сопровождается иллюстрациями, вся работа отмечается на рисунке, параллельно с этим ведется запись, которая приводит к решению проблемы.
Получив очередную порцию теоретических знаний, обучающимся предлагается рассмотреть пример по этой теории. Здесь необходимо найти, в какой четверти находится точка числовой окружности. И этот пример сопровождается иллюстрациями. Решение расписано подробно, автор комментирует каждое действие, которое происходит на экране.
Здесь урок приходит к завершению. Но на занятии должно оставаться время, чтобы закрепить материал по данной теме. Учителю необходимо подобрать такой материал по способностям обучающихся.
Тема нашего урока «ДЛИНА ДУГИ ЧИСЛОВОЙ ОКРУЖНОСТИ»
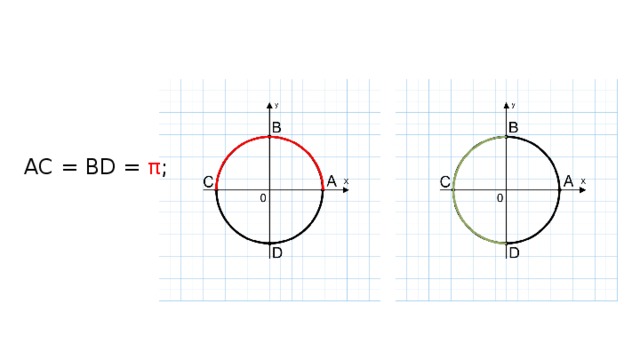
Известно, что длина окружности L вычисляется по формуле L =2πR (эль равно два пи эр), где π≈3,14 , R – радиус окружности. Для единичной окружности R=1, значит L =2π≈6,28 (эль равно два пи и приблизительно равно шесть целых двадцать восемь сотых).
Следовательно, длина половины дуги окружности АС и BD будет равна π, а длина дуги четверти окружности АВ, BC, СD, DA будет равна .
Рассмотрим примеры на нахождение длины дуги числовой окружности.
ПРИМЕР 1. В единичной окружности проведены два взаимно перпендикулярных диаметра: горизонтальный СА и вертикальный DB. Дуга АВ разделена точкой Е пополам, а точками O и F – на три равные части
(рис 1). Чему равны длины дуг EВ, OF, FВ, EO?
Решение. Так как дуга АВ – это четвертая часть длины окружности, то ее длина равна . Точкой E дуга АВ была разделена на две равные части, значит, дуги АE и EВ равны, их длины тоже равны. То есть АE = EВ=.
Точками F и O разбили дугу АВ на три равные части, то есть
АF = FO = OВ = ׃ 3 = .( равно пи на два деленное на три равно пи на шесть).
Длину дуги FВ можно найти как удвоенное произведение длины дуги АF .
FВ = 2 ∙ = ( равно два умножить на пи на шесть равно два пи на шесть равно пи на три).
И найдем длину дуги EO. Длину этой дуги можно получить из дуги EВ отбрасыванием дуги OВ. То есть EO = EВ – OВ = –= .( равно пи на четыре минус пи на шесть равно пи на двенадцать).
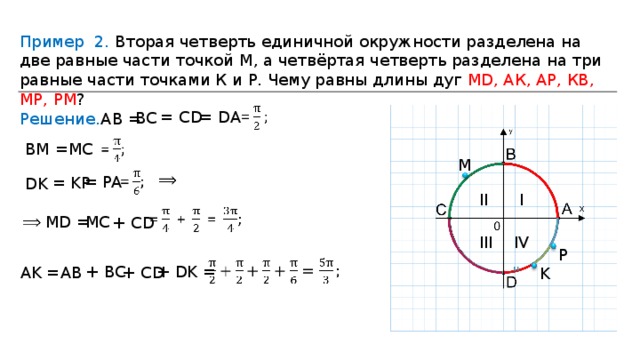
ПРИМЕР 2. Вторая четверть единичной окружности разделена на две равные части точкой М (рис), а четвертая четверть разделена на три равные части точками К и Р. Чему равны длины дуг МD, АК, АР, КВ, МР,РМ?
Решение. Очевидно, что длины дуг АВ, ВС, СD, DА равны между собой и равны пи на два. ВМ равно МС и равно пи на четыре, а DК равно КР равно РА и равно пи на шесть. Следовательно, МD = МС + СD= + = ( эм дэ равно сумме эм сэ и сэ дэ равно сумме пи на четыре и пи на два равно три пи на четыре)
АК = АВ + ВС + СD + DК = + + + = ( а ка равно сумме дуг а бэ, бэ сэ, сэ дэ, дэ ка равно пи на два плюс пи на два плюс пи на два плюс пи на шесть равно пять пи на три)
АР = АВ + ВС + СD + DР= 3∙ +2 ∙ = ( а пэ равно сумме дуг а бэ, бэ сэ, сэ дэ и дэ рэ равно сумме утроенного пи на два и удвоенного пи на шесть равно одиннадцать пи на шесть)
КВ = КР + РА + АВ = + + = ( ка бэ равно сумме дуг ка пэ, рэ а, а бэ рано сумме пи на шесть, пи на шесть и пи на два равно пять пи на шесть)
МР = МС + СD + DК + КР = + + + = ( эм пэ равно сумме дуг эм сэ, сэ дэ, дэ ка, ка пэ равно тринадцать пи на двенадцать)
РМ = РА + АВ + ВМ = + + = ( длина дуги пэ эм равна сумме длин дуг пэ а, а бэ, бэ эм равно сумме пи на шесть , пи на два и пи на четыре равно одиннадцать пи на двенадцать).
В разобранных примерах длины дуг были выражены некоторыми долями числа пи. Это и понятно, ведь длина единичной окружности равна два пи. Возникает вопрос: можно ли найти на единичной окружности такую точку Е1( е один), чтобы длина дуги АЕ1( а е один) была равна 1( единице). Поскольку π ≈ 3,14 ; ≈ 1,05; ≈ 0,79 , то единица больше чем пи на четыре, но меньше, чем пи на три. Рассуждая аналогично, можно найти точку Е2 , чтобы АЕ2 =2 , Е3, чтобы АЕ3=3 и т. д. Приблизительно отметим эти точки на единичной окружности , предварительно разделив каждую из четвертей на три равные части (рис.)
ПРИМЕР 3. Какой четверти числовой окружности принадлежит точка 30?
Решение. Нужно представить число 30 в виде t + 2πk (тэ плюс два пи ка) и подберем значение ка так, чтобы число тэ попало в отрезок [ 0, 2π] ( от нуля до двух пи включая эти числа). Поскольку 2π≈ 6,28 и 2πk ≈ 6,28k (два пи приблизительно равно шесть целых двадцать восемь сотых и два пи ка приблизительно равно шесть целых двадцать восемь сотых ка), то надо подобрать целое число k(ка) так, чтобы число шесть целых двадцать восемь сотых ка оказалось как можно ближе к числу 30. Очевидно, что ка равно четыре. Значит, 30 = 4,88 + 6,28 ∙ 4 (тридцать равно четыре целые восемьдесят восемь сотых плюс шесть целых двадцать восемь сотых, умноженное на четыре). Точка 4,88 находится в четвертой четверти, значит и точка 30 принадлежит четвертой четверти.
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Длина дуги числовой окружности

Длина дуги числовой окружности.формулы длины
Просмотр содержимого документа
«Длина дуги числовой окружности»

l – длина окружности.
l = 2π R , где π ≈ 3,14 ;
R – радиус окружности.
R = 1, значит l = 2π ≈ 6,28 .
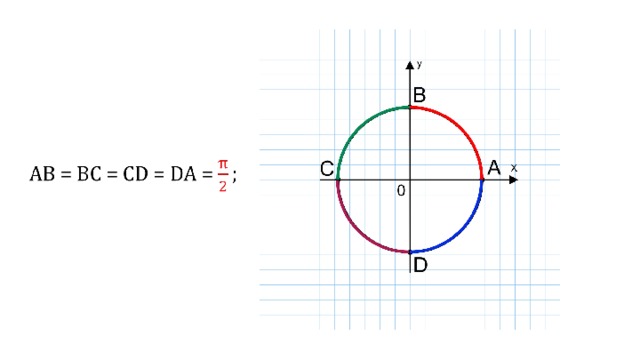

Пример 1. В единичной окружности проведены два взаимно перпендикулярных диаметра: горизонтальный AC и вертикальный BD . Дуга АВ разделена точкой Е пополам, а точками O и F – на три равные части. Чему равны длины дуг E В, OF , F В, EO ?
Пример 2. Вторая четверть единичной окружности разделена на две равные части точкой М , а четвёртая четверть разделена на три равные части точками К и Р. Чему равны длины дуг МD, АК, АР, КВ, МР, РМ ?
[spoiler title=”источники:”]
http://www.resolventa.ru/demo/diaggia6.htm
http://multiurok.ru/files/dlina-dughi-chislovoi-okruzhnosti.html
[/spoiler]
