
{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.

-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
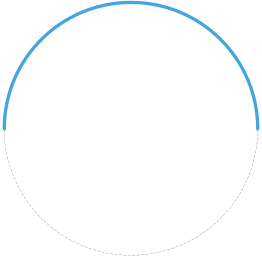
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
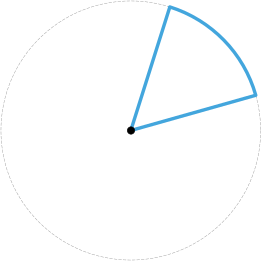
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
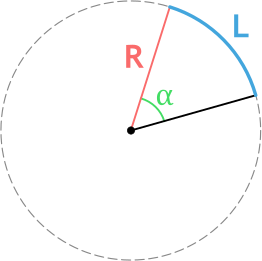
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
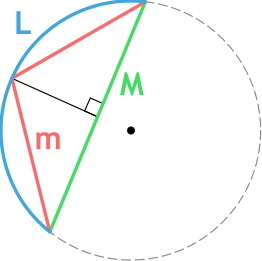
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности.

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

M N – диаметр.
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
∪ A B = ∪ C D = α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l = 2 π R
Длина дуги окружности, на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Урок математики по теме “Длина окружности и длина дуги окружности”. 9-й класс
Разделы: Математика
Класс: 9
Цель урока:
- Совершенствовать навыки решения задач на применение формул длины дуги окружности и длины окружности.
- Формировать у обучающихся регулятивные универсальные учебные действия: Учить способам самопроверки и самоанализа.
- Развивать логическое мышление, интерес к познавательной деятельности, творческие способности учащихся, математическую речь.
Тип урока: урок деятельного типа.
Оборудование: распечатки для выполнения задания «Лови ошибку!» и решения задач из различных источников для подготовки к ОГЭ и дополнительного домашнего задания, интерактивная доска, учебно-методическое пособие для подготовки к ОГЭ в 2019 году. 40 вариантов под редакцией Лысенко Ф.Ф. (у каждого ученика).
Ход урока
1. Организационный момент. Мотивация учебной деятельности
Учитель. Приветствует всех. Предлагает вспомнить тему прошлого урока и тематику домашнего задания
Предполагаемые ответы учеников (длина окружности, длина дуги окружности).
Учитель. И если сегодня у нас не будет нового теоретического материала, значит что же нам предстоит делать на этом уроке?
Предполагаемые ответы учеников (решать задачи, повторять теоретический материал).
Учитель, с учётом ответов учащихся сообщает цель урока, акцентируя внимание на эпиграфе урока, особенно на заключительном предложении, подчёркивая важность формирования у себя регулятивных универсальных учебных действий.
II. Актуализация знаний учащихся
1.1 Проверка домашнего задания (три человека работают у доски)
а) Учитель, обращаясь к классу, выясняет, кто сможет решить дополнительную задачу с объяснениями у доски и сообщает, что это была задача с сайта «Решу ОГЭ» №24 по структуре ОГЭ. Решение с использованием интерактивной доски.
1 ученик. №24. Решу ОГЭ №311 650
В треугольнике АВС: R=4,  В=72 о ,
В=72 о ,  С= 63 о , ВС =
С= 63 о , ВС =  .
.
Найти:
а) радиус окружности, описанной около треугольника;
б) длину окружности;
в) длину дуги ВС.
Решение:
а) В треугольнике АВС  А = 180 о – 135 о = 45 о . Применив следствие из теоремы синусов имеем:
А = 180 о – 135 о = 45 о . Применив следствие из теоремы синусов имеем: 
Применив свойство пропорции получим: 
б) По формуле вычисления длины окружности через полученное значение радиуса находим:  .
.
в) По формуле длины дуги окружности l =  где α = 90 о , по свойству центрального угла находим: l =
где α = 90 о , по свойству центрального угла находим: l = 
Ответ: 2; 4 ,
,  .
.
б) 2 ученик (ГВЭ) Учебник № 1101(1)
С = 6,28 · 4= 25,12
Ответ: 25,12.
в) 3 ученик. Учебник №1109(1)
а) R = 6, дуга АВ = 30 о . Найти длину дуги АВ.

Ответ:  .
.
1.2 Учитель проверяет решение домашней работы у доски, а класс выполняет самостоятельную работу по карточкам с последующей проверкой.
(Для диагностики и формирования регулятивных учебных действий использовать такой вид занятий как «Лови ошибку»).
Ответить на вопросы: «да» или «нет», заполнив таблицу
Да
2, 6, 8, 9
Нет
1, 3, 4, 5, 7
1. Окружность – это шар, все точки которого находятся на заданном расстоянии от одной данной точки. (нет)
2. Любой равносторонний треугольник является правильным? (Да)
3. Любой равносторонний четырёхугольник является правильным? (Нет, например ромб)
4. Угол, лежащий напротив радиуса – прямой. (нет)
5. Стороны треугольника пропорциональны косинусам противолежащих углов. (нет)
6. Сторона квадрата, вписанного в окружность равна. Длина этой окружности равна 12. (да)
7. Сторона правильного шестиугольника, вписанного в окружность, равна 6. Длина этой окружности равна 6. (нет)
8. Длина окружности более чем в 3 раза превышает диаметр этой окружности. (да)
9. Длина дуги прямо пропорциональна её градусной мере. (да)
1.3 Самопроверка ответов с последующей самооценкой. (Правильные ответы заготовлены для проверки).
Критерии оценивания
Менее 3 баллов
3-4 балла
5-6 баллов
7-9 баллов
«2»
«3»
«4»
«5»
III. Решение задач
1 тип (прямоугольный треугольник в окружности …)
Учитель обращает внимание на 4 и 5 вопросы «Лови ошибку» и выясняют с классом правильный ответ, подводит итог с классом: применение каких дополнительных теоретических сведений требовалось для решения задачи и правильного ответа на вопросы.
Предлагает решить задачи (Лысенко. Варианты №5,6. Задание №16), но добавить вопрос: найти С окружности.
В треугольнике АВМ АМ=12, ВМ=5, угол М=90 о . Найти радиус окружности, описанной около этого треугольника, длину окружности
Решение: АВ=13, R = 6,5; С=13 .
.
Ответ: R = 6,5; С=13 .
.
Вариант №6. Задание №16
В треугольнике ВСК ВС=8, СК=6, угол С=90 о . Найти радиус окружности, описанной около этого треугольника, длину окружности.
Решение: АВ=10, R = 5; С=10 .
.
Ответ: R = 5; С=10 .
.
IV. Физкульминутка
V. Решение задач нового типа по рассматриваемой теме
Учитель обращает внимание учеников на последний 9 вопрос. Необходимо довести до учащихся тот факт, что длина дуги окружности прямо пропорциональна её градусной мере, т.е  , где α, β – градусные меры дуг, т.е. центральные углы, а Х и У – длины этих дуг.
, где α, β – градусные меры дуг, т.е. центральные углы, а Х и У – длины этих дуг.
Учитель предлагает продолжить работу с учебно-методическим пособием по подготовке ОГЭ. Лысенко Ф.Ф. (40 вариантов).
Лысенко Вариант №13. Задание №16
На окружности с центром О отмечены точки С и Д так, что угол СОД равен 48 о . Длина меньшей дуги СД равна 34. Найти длину большей дуги.
Решение:
Пусть длина большей дуги СД равна х.
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 221.
Лысенко Вариант №14. Задание №16
На окружности с центром О отмечены точки К и L так, что угол КOL равен 76 о . Длина меньшей дуги КL равна 95. Найти длину большей дуги.
Решение:
Пусть длина большей дуги равна х. Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 355.
VI. Рефлексия учебной деятельности
- Задачи какого содержания решали на уроке? Какие из них не совсем понятны?
- Что нового узнали на уроке?
- Какие знания сегодня приобрели, приумножили, а какие умело применили.
VII. Информация о домашнем задании
Стр. 284 вопросы 1,6,7,10 № 1108 (практич.содер.; межпред. Связь) №1104(б)
Индивидуальные задания. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите длину окружности, если AB = 15, AC = 25 (теорема о касательной и секущей, проведенных к окружности из одной точки).
Дополнительные задачи
1 часть. 50 вариантов заданий. ОГЭ 2019. Под редакцией И.В.Ященко. Задание №17.
Вариант 1.
- Центр окружности, описанной около треугольника АВС лежит на стороне АВ, АС = 16, ВС = 30. Найти длину окружности.
Вариант 2
- Центр окружности, описанной около треугольника АВС лежит на стороне АВ, АС = 32, ВС = 24. Найти длину окружности.
Вариант 3.
- Сторона равностороннего треугольника равна
 . Найти длину окружности, описанной около этого треугольника.
. Найти длину окружности, описанной около этого треугольника.
2 часть
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите длину окружности, если AB = 15, AC = 25 (теорема о касательной и секущей, проведенных к окружности из одной точки).
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/673051
[/spoiler]
План урока:
Длина окружности и число пи
Длина дуги
Площадь круга
Площадь сектора
Площадь кольца и других сложных фигур
Длина окружности и число пи
Окружность представляет собой линию, а значит, у нее есть длина. Действительно, представим себе нить, опоясывающую какой-нибудь круглый предмет. Если эту нить разрезать, то ее можно будет развернуть на плоскости в отрезок. Её длина и будет длиной окружности.

Однако определить точно эту длину довольно сложно, так как окружность является «кривой» линией, а до этого в курсе геометрии мы рассматривали только длины отрезков. Для приближенной оценки длины окружности можно использовать правильные многоугольники.
Возьмем произвольную окружность и впишем в нее правильный n-угольник, и одновременно ещё один n-угольник опишем около окружности. Можно считать, что периметры этих n-угольника приближенно равны длине окружности, причем периметр вписанного многоугольника – это приближение с округлением в меньшую сторону (оценка снизу), а периметр описанного многоугольника – это уже оценка сверху.
Обычно длину окружности обозначают буквой С. Обозначим периметры вписанного и описанного многоугольника как Рв и Ро. Тогда можно записать двойное неравенство:

Далее будем увеличивать число n. При этом n-угольник будет всё плотнее «прилегать» к окружности, и тем самым его периметр будет являться все более точным приближением длины окружности.

Напомним две формулы, которые мы вывели, изучая правильные многоугольники:

Здесь аn – это сторона n-угольника, R – радиус описанной окружности, r – радиус вписанной окружности. Из второй формулы можно выразить R и подставить это выражение в первую формулу:

Здесь R радиус окружности, ав и ао – стороны вписанного и описанного многоугольника соответственно. Умножим эти равенства на n, чтобы в левой части получился периметр многоугольников:

Это неравенство позволяет для любой окружности оценить отношение длины ее окружности к ее диаметру (2R – это как раз диаметр окружности).
Можно доказать, что при увеличении n величина

при росте n, наоборот, убывает, но также стремится к пределу. Более того, оказывается, что эти пределы у обоих выражений одинаковы, то есть являются одним и тем же числом. Это значит, что и само отношение длины окружности к диаметру является этим же числом, которое традиционно обозначается буквой π. Записать этот факт можно так:

Ещё раз обратите внимание, что число π (читается как «число пи») не зависит от диаметра окружности или расположения ее центра, это некоторое постоянное число. Обычно его определяют так:

Чем большее n мы сюда подставим, тем более точную оценку числа π мы получим. Ещё Архимед использовал в этом неравенстве n = 96 (это значение было удобно взять, так как соответствующие значения синуса и тангенса угла 180°/96 уже умели вычислять в Древней Греции). Если мы воспользуемся калькулятором, то при n = 96 получим:

Вы можете и сами найти более точную оценку числа пи, используя неравенство (1) и калькулятор, умеющий высчитывать синусы и тангенсы. Попробуйте, например, подставить в него n = 1 000 000.
Используя метод многоугольников, Людольфу ван Цейлену в 1596 г. удалось вычислить 20 верных десятичных знаков числа пи после запятой:

Дальнейший прогресс в этой области был связан уже с использованием более сложных методов, основанных на бесконечных рядах чисел. Также в XVIII в. было доказано, что число π – иррациональное, то есть оно является бесконечной непериодической десятичной дробью. На сегодня даже на обычном персональном компьютере можно вычислить триллионы цифр после запятой в числе π. В большинстве школьных задач число π принимается равным 3,14. Однако если в задаче не просят округлить ответ, то вместо числа π вообще не надо ничего подставлять.
Из определения числа π вытекает формула для вычисления длины окружности c радиусом R или диаметром D:

Задание. Найдите длину окружности, если ее радиус составляет 5 см.
Решение. Просто подставляем в формулу число 5:

Обратите внимание, что вместо числа π НЕ надо подставлять его приближенное значение, так как в условии не говорится, что ответ надо округлять. Только та запись, в которой число π оставлено как есть, является точным, а не приближенным ответом.
Ответ: 10π см.
Задание. Диаметр окружности составляет 40 см. Вычислите приближенно ее длину, принимая число π примерно равным 3,14.
Решение. Так как ответ надо будет округлить, то вместо числа π подставим значение 3,14:

Ответ: 125,6 см.
Задание. Длина окружности составляет 100 см. Вычислите приближенно её радиус.
Решение. Из формулы для длины окружности легко получить формулу и для вычисления радиуса:

Ответ: 15,9 см.
Задание. Вычислите радиус Земли, если известно, что длина экватора составляет 40 000 км.
Решение. Задача аналогична предыдущей, только вместо длины окружности надо подставить 40 000 км:

Ответ: ≈ 6369 км.
Задание. Автомобиль проехал 1978 метров, при этом одно из его колес совершило 1000 оборотов. Вычислите приближенно диаметр этого колеса.
Решение. В таких задачах неявно предполагается, что колесо плавно катится по дороге, а не скользит по нему. Можно посчитать, какое передвижение соответствует 1 обороту колеса:
1978 м : 1000 обор. = 1,978 м/об
Это величина как раз является длиной окружности колеса. Тогда легко найти и диаметр:

Ответ: 63 см.
Длина дуги
Иногда требуется вычислить не длину всей окружности, а только лишь длину ее части, то есть дуги.

Напомним, что дуги имеют такую характеристику, как градусную меру, которая равна величине центрального угла, на который дуга опирается. Оказывается, что длина дуги окружности и ее градусная мера связаны. Для начала попытаемся найти длину дуги величиной в 1°. Напомним, что вся окружность составляет 360°. Значит, ее можно разбить на 360 маленьких дуг по 1°. Так как все эти дуги одинаковы, то длина каждой из них будет в 360 раз меньше длины все окружности:

Теперь предположим, что нам надо найти длину дуги с градусной мерой α, причем α – это целое число. Тогда мы можем разбить эту дугу на α маленьких дуг по 1°, и ее длина будет равна сумме их длин:

Задание. На окружности с радиусом 6 см отмечена дуга величиной в 30°. Найдите ее длину.
Решение. Просто подставляем в формулу числа:

Ответ: π см.
Задание. На железнодорожном пути есть закругленный участок радиусом 5 км, а его длина составляет 400 м. Какова градусная мера этого закругления? Дайте приближенный ответ без использования числа π.
Решение. Выведем из формулы выражение для угла α:

Ответ: 4,6°.
Задание. Длина дуги окружности равна 20 см, ей соответствует центральный угол в 60°. Каков радиус окружности? Ответ не округляйте.
Решение. Теперь из формулы выражаем радиус окружности:

Ответ: 60/π см.
Задание. Точки А и В разбивают окружность на две дуги. Длина меньшей дуги равна 63, а опирается она на центральный угол в 28°. Какова длина большей дуги?
Решение. Сначала найдем радиус окружности:

Вся окружность составляет 360°. Если градусная мера меньшей дуги – это 28°, то у большей дуги градусная мера (обозначим ее как β) определяется так:

Ответ: 747 см.
Задание. Какой должна быть градусная мера дуги, чтобы ее длина в точности совпадала с длиной радиуса?
Решение. Запишем формулу:

Ответ: ≈ 57,32°.
Площадь круга
Напомним, что кругом называется часть плоскости, ограниченная окружностью. Для нахождения площади круга можно использовать все тот же метод многоугольников, который мы применили для нахождения длины окружности и вычисления числа π.
Возьмем окружность и впишем в нее n-угольник. В свою очередь в него впишем окружность.

Выпишем изученные нами ранее две формулы:

Здесь r и R – радиусы вписанной и описанной окружности соответственно, Р – периметр многоугольника, Sмног. – площадь многоугольника. С ростом n периметр многоугольника приближается к длине описанной окружности, что можно записать в таком виде

Одновременно с этим и площадь многоугольника приближается к площади круга (имеется ввиду больший, то есть описанный круг), что позволяет вычислить ее:

Задание. Определите площадь круга, ограниченного окружностью 10 см.
Решение. В этой задаче надо просто подставить числа в формулу:

Ответ: 100π см2.
Задание. Площадь круглого бассейна составляет 10 м2. Каков его радиус? При расчете примите число π равным 3,14.
Решение. Здесь надо из формулы площади получить выражение для вычисления радиуса:

Ответ: ≈ 1,8 м.
Задание. Во сколько раз увеличится площадь круга, если его радиус увеличится в 2 раза?
Решение. Пусть радиус исходного круга – это R. Тогда его площадь рассчитывается так:

Ответ: в 4 раза.
Примечание. В общем случае увеличение радиуса круга в k раз приводит к увеличению его площади в k2 раз.
Задание. Ваня и Петя решили купить пиццу. Сначала Ваня заметил пиццу диаметром 30 см, цена которой – 300 рублей. Но тут же Петя обнаружил на витрине такую же пиццу диаметром 40 см, которая стоила уже 450 рублей, и предложил ее купить. Ваня сказал, что этот невыгодная покупка, ведь радиус у второй пиццы больше только на треть, а цена больше уже наполовину. Прав ли Ваня?
Решение. Масса пиццы пропорциональна их площади. У второй пиццы радиус больше в 4/3 раза (так как 40/30 = 4/3), значит, площадь у нее больше в

Получается, что вторая пицца больше в 1,78 раза, а цена у нее выше только в 1,5 раза. То есть выгодней купить именно вторую, то есть большую пиццу.
Ответ: Ваня не прав, лучше купить пиццу диаметром 40 см.
Примечание. В этой задаче можно было посчитать площадь каждой пиццы, а потом поделить их стоимость на площадь и получить цену 1 см2 пиццы в каждом варианте. Ответ бы при этом не изменился.
Задание. Завод изготавливает круглые столы радиусом 1,5 метра. Их поверхность надо покрывать лаком, причем на каждый 1 м2 поверхности необходимо тратить 20 г лака. Лак закупается раз в месяц, и в течение ближайшего месяца завод должен изготовить 5000 столов. Сколько лака должен закупить завод на ближайший месяц?
Решение. Считаем площадь поверхности каждого стола:

Ответ: 706,5 кг.
Площадь сектора
Напомним, что сектором называется часть круга, образованная двумя его радиусами. Если же в круге проведена хорда, то она отсекает от него сегмент:

Проведем из центра окружности 360 радиусов, причем угол между соседними радиусами будет ровно 1°. В результате мы разобьем окружность на 360 одинаковых секторов, площадь каждого такого сектора будет в 360 раз меньше площади круга:

Теперь рассмотрим сектор, который образован дугой величиной в α градусов. Если α – целое число, то такой сектор можно составить из α секторов, каждый из которых составляет по 1°. Тогда площадь сектора круга будет определяться формулой:


Задание. Круговой сектор опирается на дугу в 45°, а его радиус составляет 40. Определите площадь этого сектора.
Решение. Используем выведенную формулу:

Ответ: 12,5π.
Задание. Площадь сектора равна 200 см2. Он опирается на дугу в 30°. Каков радиус кругового сектора? При решении примите π равным 3,14.
Решение. Из формулы площади сектора выразим радиус окружности:

Ответ: ≈ 27,6 см.
Задание. На сторонах произвольного прямоугольника построены полукруги:

Докажите, что площадь полукруга, опирающегося на полуокружность, равна сумме площадей полукругов, опирающихся на катеты.
Решение. Полукруг представляет собой сектор с центральным углом α = 180°, поэтому его площадь может быть рассчитана так:

Заметим, что эти стороны являются диаметрами полукругов. Обозначим как D1 диаметр полукруга, опирающегося на гипотенузу, а два других диаметра как D2 и D3. Тогда можно выполнить преобразования:

Именно это равенство нам и требовалось доказать.
Теперь рассмотрим более сложную задачу, в которой необходимо определить площадь сегмента.
Задание. В окружности радиусом 20 проведена хорда длиной 12. Она разбивает окружность на два круговых сегмента. Найдите площадь каждого из них. При расчете примите π ≈3,14.

Чтобы найти площадь меньшего сегмента, можно вычесть из площади кругового сектора площадь треугольника АВО. Для нахождения обоих площадей в любом случае надо сначала определить величину угла ∠АОВ. Это можно сделать, применив теорему косинусов:

Далее надо рассчитать площадь ∆АВС. Это можно сделать с помощью разных формул, мы используем формулу с синусом угла. Для этого предварительно вычислим синус ∠АОВ, применив основное тригонометрическое тождество:

Осталось вычесть из площади сектора площадь ∆АВС, чтобы найти площадь кругового сегмента S1:

Примечание. В подобных задачах ответы и промежуточные ответы могут немного отличаться в зависимости от того, с какой точностью берется число π, вычисляется ∠АОВ и его синус, и как именно округляются промежуточные результаты и т. п. Более точные расчеты показывают, что в описанной задаче величины S1 и S2 примерно равны:

Площадь кольца и других сложных фигур
Если какая-либо фигура образована с помощью нескольких окружностей, то найти ее площадь можно, представив ее в виде суммы площадей нескольких более простых фигур. В качестве простейшего примера можно привести кольцо. По сути оно представляет собой круг, в котором есть круговое отверстие:

Если обозначить наружный радиус кольца буквой R, а радиус отверстия буквой r, то площадь кольца можно найти, вычтя из площади большего круга площадь отверстия:

Задание. Внешний радиус кольца составляет 20 см, а радиус отверстия в нем равен 15 см. Определите площадь кольца.
Решение. Подставляем числа в формулу:

Ответ: 175π.
Задание. Есть диск радиусом 1 метр. Необходимо вырезать в нем отверстие так, чтобы масса диска уменьшилась в два раза. Какой радиус должен быть у отверстия?
Решение. Можно считать, что масса диска пропорциональна его площади, поэтому нам надо, чтобы площадь диска уменьшилась вдвое. Начальная площадь диска определяется так:

Площадь кольца должна быть вдвое меньше, то есть она будет составлять π/2. Если радиус отверстия мы обозначим как r, то можно составить уравнение:

Ответ: ≈ 70,7 см.
В прямоугольной плите с габаритами 180 и 60 см сделано 27 отверстий диаметром 10 см. Вычислите площадь этой плиты. Считайте, что π ≈ 3,1416, и округлите ответ до целых.

Решение. Надо найти площадь плиты без учета отверстий, а потом вычесть из нее площадь всех отверстий. Площадь плиты равна произведению ее сторон

Ответ: ≈ 8679 см2.
Задание. Из вершин квадрата со стороной а проведены дуги радиусом а/2. В результате получили следующую фигуру:

Найдите заштрихованную площадь.
Решение. Площадь заштрихованной области может быть получена, если из площади квадрата мы вычтем площади 4 секторов. Площадь квадрата рассчитывается так:

Задание. В квадрате, сторона которого обозначается буквой а, из вершин провели дуги, чей радиус совпадает со стороной квадрата. В результате в центре квадрата получили следующую фигуру:

Определите, какую долю квадрата занимает эта центральная фигура. Ответ дайте в процентах и округлите его до десятых.
Решение. Задача решается в несколько действий, причем нам потребуется составить формулы для вычисления площадей вспомогательных фигур. Сначала найдем площадь маленького треугольника с «кривыми» сторонами, для чего используем такое построение:

Площадь, которую мы пытаемся найти, обозначена здесь как S1. Ее можно получить, просто вычтя из площади квадрата (она составляет а2) площади двух секторов и площадь треугольника. Треугольник на рисунке – равносторонний, ведь и сторона квадрата, и радиусы окружностей равны величине а. Тогда каждый его угол составляет 60°, и его площадь можно найти так:

Также мы можем найти центральные углы обоих секторов. Так как углы в квадраты составляют 90°, а в равностороннем треугольнике 60°, то эти углы окажутся равными 90° – 60° = 30°. Тогда площадь сектора вычисляется по формуле:

На следующем шаге вычислим площадь другой фигуры:

Попытаемся выразить величину S2. Для этого из площади квадрата надо вычесть площадь сектора, у которого центральный угол составляет 90°. Найдем площадь этого сектора:

Здесь мы ищем площадь S3. Обратите внимание, что ее можно выразить через уже найденные нами величины S1 и S2:

Мы составили выражения для всех необходимых нам вспомогательных фигур. Теперь вернемся к исходному рисунке и отметим на нем эти вспомогательные фигуры:

Итак, мы составили выражение для вычисления площади центральной фигуры. По условию надо указать, сколько процентов она составляет от площади всего квадрата. Для ответа на этот вопрос поделим площадь фигуры на площадь квадрата и умножив это отношение на 100%:

Ответ: 31,5%.
В рамках этого урока мы узнали, как вычислять длину окружности и дуги, площади круга, сектора, сегмента, кольца и других фигур, одна или несколько сторон которых представляют собой дуги окружности. Эти навыки могут пригодиться и в реальной жизни, так как именно от площади многих предметов часто зависит потребность в краске, лаке, клее и т. п.
Arc length is defined as the distance between the two points placed on the circumference of the circle and measured along the circumference. Arc length is the curved distance along the circumference of the circle. Length of the arc between two points is always greater than the chord between those two points.
What is Arc Length?
The arc length is defined as the circular distance between two points along the circumference of the circle. The length of the arc is directly dependent on the radius and central angle of the circle. The central angle is the angle subtended by the endpoints of the arc to the center of the circle. It is denoted by θ. It is measured both in degrees and radians. The figure given below shows the arc AB when the radius is r and the central angle is θ.

Arc Length Formula
Length of the arc is calculated using different formulas, the formula used is based on the central angle of the arc. Central angle is measured in degrees or radians, and accordingly, the length of an arc of the circle is calculated. For a circle, the formula for arc length formula is θ times the radius of the circle.
| Arc Length Formula (θ in degrees) | s = 2×π×r ×(θ/360°) |
| Arc Length Formula (θ in radians) | s = θ × r |
| Arc Length Formula (Integral Form) | s = ∫√(1 + (dy/dx)2dx |
There are different cases that are used accordingly to find the required Arc Length
Case 1: When Radius and Angle are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)… (1)
where
r is the radius of the circle
θ is the angle in degrees
L is the Arc lengthArc length when the angle is represented in radians
1 radian = π/180°
Substituting the value of radian in equation (1)
L = 2πr × (θ × / 360)
L = r θ…(2)
where,
r is the radius of the circle
θ is the angle in radians.
Case 2: When Area and Central Angle of the Arc are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)
where,
r is the radius of the circle
θ is the angle in degreesWe need to find the radius of the circle from the given area. After finding the radius, we will substitute the value of radius in the formula.
Area of the circle = πr2
Example: If area of the circle is 314 m2 and centeral angle of the arc is π radian find the length of the arc.
Sloution:
πr2 = 314 m2
r2 = 314/π (π = 3.14)
r2 = 314/3.14
r2 = 100
r = √100 = 10 m
Length of the arc with angle π radians will be:
L = r θ
L = 10 × π
L = 10 × 3.1415
L = 31.415 m
The value of r can be used in the same formula, as discussed above.
Case 3: Arc length In Integral Form
Arc length in integral form is given by:
L = ∫√(1 + (dy/dx)2)dx
where,
Y is the f(x) function
limit of integral is [a, b]
How to Find Arc Length?
Use the steps given below to find the Arc length of the given arc.
Step 1: Mark the central angle and length of the radius of the given arc.
Step 2: Use the formula as given above according to the value of the angle in degrees or radians accordingly.
Step 3: Simplify the above equation to get the required answer.
Also, Check
- Equation of a Circle
- Degrees To Radians
- Radians to Degrees
Solved Examples on Arc Length
Example 1: Find the length of the arc with a radius of 2m and angle π/2 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 2m and θ = π/2 radians
Length of arc = 2 × π/2
Length of arc = π
(π = 3.1415)
Length of arc = 3.1415 m
Thus, the length of the arc is 3.1415 m.
Example 2: Find the length of the arc of function f(x) = 8 between x =2 and x = 4.
Solution:
The formula to calculate the arc length for the function is given by:
L = ∫√(1 + (dy/dx)2)dx
The limit of integral is [a, b]
Substituting the values a = 2, b = 4, and y = 6 or dy/dx = 0 in the above formula,
L = ∫√(1 + (0)2)dx
L = ∫√1 dx
L = ∫1 dx
L = x
(Integral of 1 is x)
The limit of integral is [2, 4]
L = (4 – 2)
L = 2
Thus, the length of the arc of function f(x) = 8 between x = 2 and x = 4 is 2.
Example 3: Find the length of the arc with a radius of 5cm and an angle of 60°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 5cm and θ = 60°
Length of arc = 2πr × (60 / 360)
Length of arc = 2πr × 1/6
Length of arc = 2 × 3.1415 × 5/6
(π = 3.1415)
Length of arc = 5.235cm
Thus, the length of the arc is 5.235cm
Example 4: Find the length of the arc with a radius of 0.5m and an angle of π/4 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 0.5m and θ = π/4 radians
Length of arc = 0.5 × π/4
Length of arc = 0.392 m
(π = 3.1415)
Thus, the length of the arc is 0.392 m
Example 5: Find the length of the arc with a radius of 10cm and an angle of 135°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 10cm and θ = 135°
Length of arc = 2πr × (135/360)
Length of arc = (2 × 3.1415 × 10 × 135)/360°
(π = 3.1415)
Length of arc = 23.56cm
Thus, the length of the arc is 23.56cm.
Example 6: Find the length of the arc with a radius of 20mm and angle π/6 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 20mm and θ = π/6 radians
Length of arc = 20 × π/6
Length of arc = 10.47 mm
(π = 3.1415)
Thus, the length of the arc is 10.47 mm
Example 7: Find the length of the arc with a radius of 2 cm and an angle of 90°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 2cm and θ = 90°
Length of arc = 2πr × (90 / 360)
Length of arc = 2πr × 1/4
Length of arc = 2 ×3.1415 × 2 × 1/4
(π = 3.1415)
Length of arc = 3.1415 cm
Thus, the length of the arc is 3.1415 cm.
FAQs on Arc Length
Question 1: What is the Arc Length of a Circle?
Answer:
Arc length of a circle is the length made by the arc which is measured along its circimference.
Question 2: Length of the arc is measured in which unit?
Answer:
Length of arc is of a circle is either measured in m or in cm.
Question 3: Does arc length is measured in radians?
Answer:
Angles are measured in radians and arc length is a measurement of distance, thus it cannot be measured in radians.
Question 4: How do you find the circumference if the arc length (l) and central angle (θ) are given?
Answer:
When arc length (l) and central angle (θ) is given then the circumference by the formula
Arc Length (L) / Circumference = θ/360º
Last Updated :
20 Jan, 2023
Like Article
Save Article

