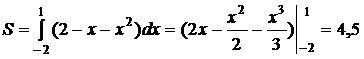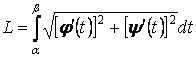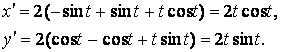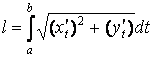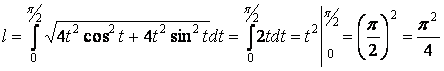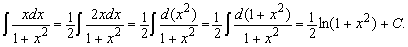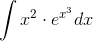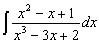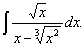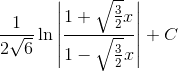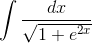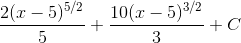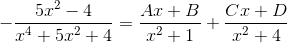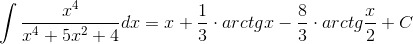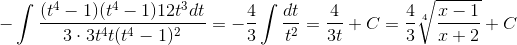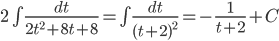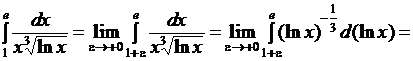Как найти длину дуги интеграл онлайн

Как найти длину дуги интеграл онлайн

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:

график функции y=x^2

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:

В более общем случае, если у нас задана функция

в декартовых координатах и стоит задача найти длину дуги этой кривой между точками

и
,
нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение

означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Источник

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • длина:дуги:x,:0,:1

  • длина:дуги:sqrt{1-x^{2}}

  • длина:дуги:ln(sec(x)),:[0,:frac{pi}{4}]

  • длина:дуги:y=2x^{2}+3,:0le xle 1

  • Показать больше

Описание

Найдите длину дуги функций между интервалами шаг за шагом

arc-length-calculator

длина дуги y=2x^{2}+3, 0le xle 1

ru

Блог-сообщения, имеющие отношение к Symbolab

  • Practice, practice, practice

    Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Калькулятор длины дуги кривой линии в декартовых координатах

    Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции :

    Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:

    В более общем случае, если у нас задана функция в декартовых координатах и стоит задача найти длину дуги этой кривой между точками и , нам необходимо вычислить интеграл:

    В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции , а затем полученное выражение возвести в квадрат.

    Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

    Вычислить длину дуг кривых заданных параметрическими уравнениями онлайн калькулятор

            Пусть кривая задана уравнениями в параметрической форме

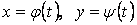
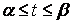
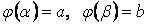
    где         и         .
            Длина дуги кривой

            Прежде, чем Вы начнёте скачивать свои варианты, попробуйте найти интеграл по образцу, приведённому ниже для варианта 27.

            Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6

            Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12

        Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18

        Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24

        Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30

            Задача 18.27. Вычислить длину дуги кривой, заданной параметрическими уравнениями.

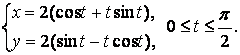
    Решение

            Найдём производные

            Длина дуги кривой, заданной параметрически, ищется по формуле

            Подставляя данные, получим

            Ответ:         .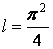

    Вычислить длину дуг кривых заданных параметрическими уравнениями онлайн калькулятор

    Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
    где параметр t лежит в промежутке [a, b],
    и вы можете указать свои границы.
    Задайте также функции x и y, зависящих от параметра.

    Примеры кривых

    Название кривой Уравнение
    Окружность
    Спираль
    Дельтоида
    Астроида
    Гипоциклоиды
    Кардиоида
    Нефроида
    Эпициклоиды
    Бабочка
    Фигуры Лиссажу
    Сердце

    Правила ввода выражений и функций

    3.14159.. e Число e – основание натурального логарифма, примерно равно

    2,7183.. i Комплексная единица oo Символ бесконечности – знак для бесконечности

    © Контрольная работа РУ – калькуляторы онлайн

    Где учитесь?

    Для правильного составления решения, укажите:

    [spoiler title=”источники:”]

    http://www.kvadromir.com/kuznecov_integral_18.html

    http://www.kontrolnaya-rabota.ru/s/grafik/parametr/

    [/spoiler]

    Источник

    Если линия задана параметрическими уравнениями (x=varphi _{1}left(t right), y=varphi _{2}left(t right), z=varphi _{3}left(t right)), где (varphi _{i}left(t right) left(i=1,2,3 right)) – дифференцируемые функции аргумента (t) и (left(alpha leq tleq beta right)), то длина дуги линии вычисляется по формуле: [S=int_{alpha }^{beta }{sqrt{x’^{2}+y’^{2}+z’^{2}}}dt.] В случае, когда плоская линия задана уравнением [y=fleft(x right),] где (fleft(x right)) – дифференцируемая функция и (aleq xleq b), то [S=int_{a}^{b}{sqrt{1+y’^{2}}}dx.] Если плоская линия задана уравнением [rho =rho left(varphi right) left(alpha leq t right)] в полярных координатах, то [S=int_{alpha }^{beta }{sqrt{rho ^{2}+rho ‘^{2}}}dvarphi.]

    С помощью нашего решебника вы можете вычислить длину дуги кривой. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку “Решить”.

    Вычислить длину дуги кривой 

    arc length of y=x^2 from x=0 to 1
    length of e^-x^2 for x=-1 to x=1

    Вычислить длину дуги кривой заданной параметрически

    arclength x(t)=cos^3 t, y(t)=sin^3 t for t=0 to 2pi
    length of the curve {x=2cos(t), y=2sin(t), z=t} from 0 to 7

    Вычислить длину дуги кривой

    arc-length (t,t,t,t^3,t^2) from 1 to Pi

     

    Похожие публикации: математика

    Источник

    Вычисление интегралов

    Множество всех первообразных функции f(x) (дифференциала f(x)dx) называется неопределенным интегралом от этой функции и обозначается ∫f(x)dx.

    • Решение онлайн
    • Видеоинструкция
    • Также решают

    С помощью данного онлайн-калькулятора можно вычислять любые интегралы. Например, найти интеграл x3sin(x2). Запишем как x^3*sin(x^2) и нажимаем кнопку Получить решение.

    Если интеграл определенный, например, 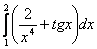решение интеграла онлайн, то записываем 2/x^4+tan(x), в качестве пределов интегрирования указываем 1, 2.

    Примечание: число “пи” (π) записывается как pi; знак “бесконечность” (∞) ≡ infinity

    Примеры правильной записи некоторых выражений

    Таблица интегралов

    Приемы нахождения неопределенных интегралов

    Способы нахождения неопределенных интегралов:

    1. Подведение под знак дифференциала:

    2. Интегрирование по частям: ∫xexdx
    3. Простейшие преобразования подынтегрального выражения (пример):
    4. Интегрирование рациональных дробей:
    5. Интегрирование простейших иррациональностей:
    6. Интегрирование выражений, содержащих тригонометрические функции: ∫cos4(x)sin3(x)dx

    Пример 1. Вычислить ∫(3x+15)17dx.

    Решение.

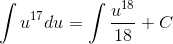
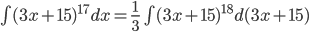
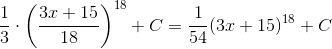
    Возводить двучлен в 17-ю степень нецелесообразно. Исходя из табличного интеграла , получаем

    = .

    Пример 2. Вычислить .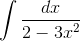

    Решение.

    Аналогично предыдущему,

    =

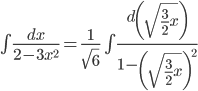
    Пример 3. .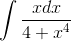

    Решение. Поскольку

    , то .

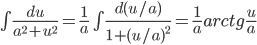
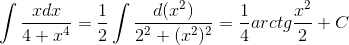
    Пример 4. Вычислить

    Решение. Так как

    , то .

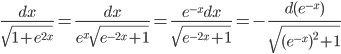
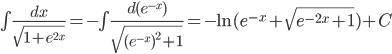
    Пример 5. Вычислить .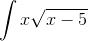

    Решение.

    Применим подстановку 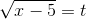. Отсюда x-5=t2, x=t2+5, dx=2tdt.

    Подставив в интеграл, получим

    =

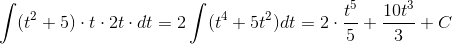
    Пример 6. Вычислить ∫x2exdx.

    Решение.

    Положим u=x2, dv=exdx; тогда du=2xdx, v=ex. Применим формулу интегрирования по частям:

    ∫x2exdx=x2ex-2∫xex.

    Мы добились понижения степени x на единицу. Чтобы найти ∫xex, применим еще раз интегрирование по частям. Полагаем u=x, dv=exdx; тогда du=dx, v=ex и

    ∫xex=x2ex-2xex+2ex+C.

    Пример 7. Вычислить .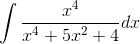

    Решение. Выделяя целую часть, получим: .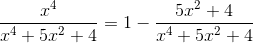

    Учитывая, что x4+5x2+4=(x2+1)(x2+4), для второго слагаемого получаем разложение



    Приводя к общему знаменателю, получим равенство числителей:

    -5x2–4=(Ax+B)(x2+4)+(Cx+D)(x2+1).

    Приравнивая коэффициенты при одинаковых степенях x, получаем

    x3: 0=A+C

    x2: -5=B+D

    x: 0=4A+C

    x0: -4=4B+D

    Отсюда находим A=C=0, B=1/3, D=-16/3.

    Подставляя найденные коэффициенты в разложение и интегрируя его, получаем:

    Пример 8. Вычислить .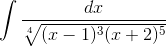

    Решение. Так как

    ,

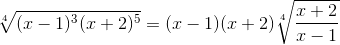
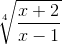
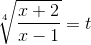
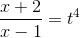
    то подынтегральное выражение есть рациональная функция от x и ; поэтому введем подстановку:

    ; ,

    откуда

    ; ; ;.

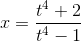
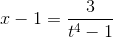
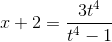
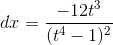
    Следовательно,

    Пример 9. Вычислить .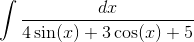

    Решение.

    Подынтегральная функция рационально зависит от sinx(x) и cos(x); применим подстановку tgx/2=t, тогда

    , , и

    =

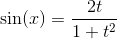
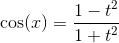
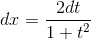
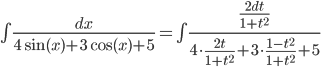
    Возвращаясь к старой переменной, получим

    = .

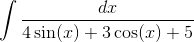
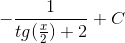
    Пример 10. Вычислить .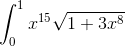

    Решение.

    Произведем замену 1+3x8 = z2. Тогда , ;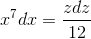

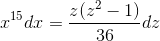
    таким образом,

    .

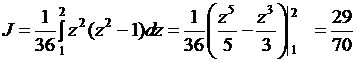
    Следует обратить внимание, что при замене переменной в определенном интеграле пределы интегрирования в общем случае изменяются.

    Пример 11.Вычислить несобственный интеграл 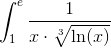или доказать его расходимость.

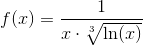
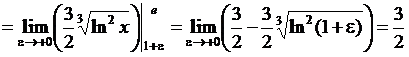
    Решение. Подынтегральная функция не ограничена в окрестности точки x=1. На любом же отрезке [1+ε;e] она интегрируема, так как является непрерывной функцией. Поэтому



    .

    Пример 12. Вычислить несобственный интеграл 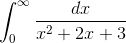или доказать его расходимость.

    Решение.

    Подынтегральная функция непрерывна и интегрируема на R. По определению

    = =

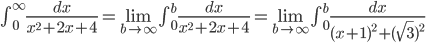
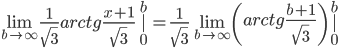
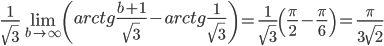
    Интеграл сходится.

    Пример 13. Найти площадь фигуры, ограниченной параболой y=x2 и прямой x+y=2.

    Решение.

    Найдем абсциссы точек пересечения параболы y=x2 и прямой y=2-x. Решая уравнение x2=2-x, находим x1=-2, x2=1. Так как фигура ограничена сверху прямой, а снизу параболой, по известной формуле находим

    .

    Источник

    Добавить комментарий