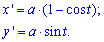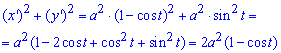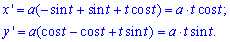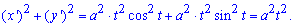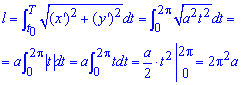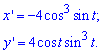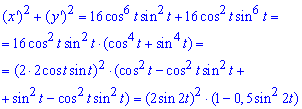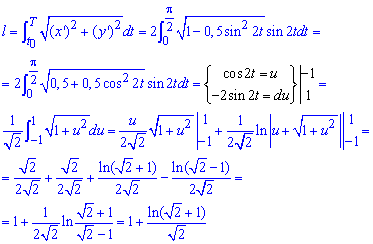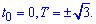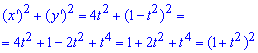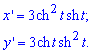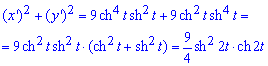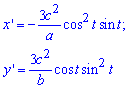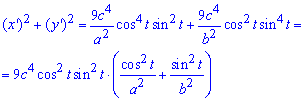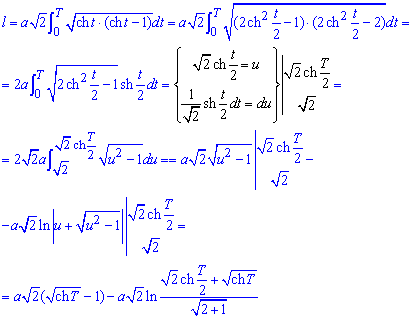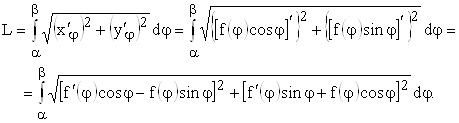Как найти длину дуги кривой заданной параметрически

Если кривая C задана уравнениями x=x(t), y=y(t) (t[t₀;T]), где x(t) и y(t) непрерывные на [t₀;T] функции, то длина дуги кривой С равняется определенному интегралу

Из формулы длины дуги кривой, заданной параметрически видим, что здесь нужно хорошо знать производные элементарных функций и иметь отличные знания c интегрирования. Как это выглядит на практике Вы можете увидеть с готовых ответов до заданий.
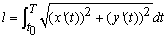
Примеры подобрано из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича). 

Для изучения основных моментов схема интегрирования и формулы вычисления дуги кривой, заданной в параметрической форме будут повторяться из примера в пример.
Часть заданий обязательно проиллюстрируем графиками кривых.

Как найти длину дуги, заданной в параметрическом виде?

Пример 2.127-2443 Найти длину дуги кривой, заданной в параметрическом виде
 x=a(t-sin(t)),  y=a(1-cos (t)), tє[0;2pi].
(См. 2.100)

Вычисление: Найдем производные по переменной t функций:

Пределы интегрирования берем из условия: [0;2pi].
Выражаем подинтегральную функцию:

Интегрированием находим длину дуги кривой на заданном отрезке:

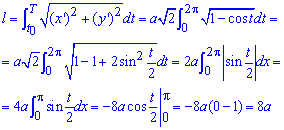
Для выведения формулы использовали известные тригонометрические формулы.
Длина дуги равна 8a единиц.

Пример 2.128 (2444) Найти длину дуги кривой, заданной параметрически
x=a(cos(t)+t*sin(t)),  y=a(sin(t)-t*cos(t)), tє[0;2*Pi]. (См. 2.103)
Вычисление: Вычисляем производную по переменной t от параметрических уравнений координат функции:

Пределы интегрирования записываем из начального условия: [0;2*Pi].
Складываем подинтегральную функцию:

Ее вид чрезвычайно прост, а длина дуги параметрической кривой через интеграл вычисляется быстро:

Пример 2.129 (2442) Найти длину дуги кривой, заданной параметрически
x=cos⁴(t), y=sin⁴(t).
Вычисление: Найдем производные по переменной t от параметрически заданных координат:

Имеем пределы интегрирования:
[0;Pi/2], поскольку функция принимает только положительные значения.
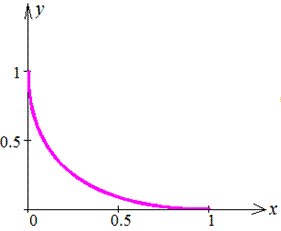
График кривой приведен на рисунку

Складываем уравнение подинтегральной функции:

Однократно применив замену переменных и метод интегрирования частями находим длину дуги кривой:

Интеграл достаточно распространен для такого сорта примеров, поэтому вспомните все формулы интегрирования, которые в результате дают логарифм.

Пример 2.130 Найти длину дуги кривой, заданной параметрически
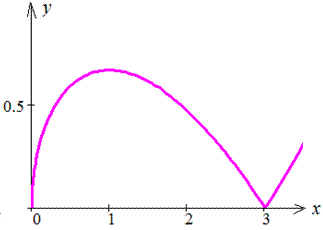
x=t²,y=t-t³,

Вычисление: Первым делом находим производные параметрически заданных координат по переменной t:
x’=2t; y’=1-t².

Крайние точки известны: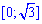
, отсюда нужно определить чему равен параметр:
из условия y=0 определяем 
Функция симметрична относительно оси Ox, поэтому принимаем 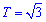 и результат интегрирования умножаем на 2.
График кривой на положительной части оси абсцисс изображен ниже

Составим уравнение подинтегральной функции:

Последним шагом находим длину дуги кривой на заданном отрезке:

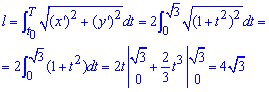
Интеграл достаточно быстро вычисляется.

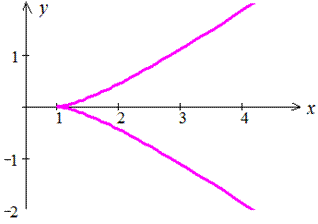
Пример 2.131 (2445.1) Найти длину дуги кривой, заданной в параметрическом виде
 x=ch³(t), y=sh³(t), [0;T]
Вычисление: Найдем производные от гиперболичного косинуса и синуса по t:

Пределы интегрирования известны: [0;T].
График кривой приведен на рисунке 

Вычислим подинтегральную функцию:

Учитывая формулы для гиперболичных функций при вычислении интеграла синус гиперболический от двойного угла вносим под дифференциал.
В результате придем к формуле, которую и без замены переменных можем проинтегрировать.
 

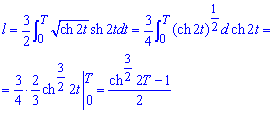
Пример 2441 Найти длину дуги эволюты эллипса, заданной параметрически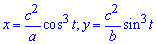
 
Вычисление: Найдем производные параметрически заданных координат эволюты эллипса:

Пределы интегрирования: [0;Pi/2] (оси координат являются осями симметрии).
График эволюты эллипса имеет вид

Складываем уравнение подинтегральной функции:

Чтобы найти длину дуги эволюты эллипса придется превратить подинтегральную функцию, потом свести ее под известные интегралы.
Чтобы облегчить чтение формул на середине вычислений выполняем замену переменных и, соответственно, пересчет пределов интегрирования.
 
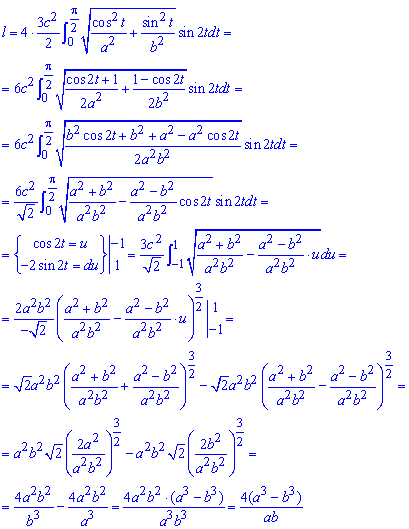
Также последние строки показывают, что умение работать с дробями Вам тоже пригодятся.
Если не упрощать, то получим тяжелую для чтения формулу с иррациональными слагаемыми.

Пример 2445 Найти длину дуги кривой, заданной параметрически
x=a(sh(t)-t), x=a(ch(t)-1, tє[0;T].
Вычисление: Вычислим производные от параметрических координат кривой:
x’=a(ch(t)-1;
y’=a*sh(t).
Пределы интегрирования заданы: [0;T].
Подносим к квадрату производные параметрических координат линии:

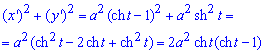
За формулой находим длину дуги кривой:
для этого превращаем подынтегральную функцию, а дальше методом замены переменных вычисляем интеграл:

Конечная формула длины дуги кривой содержит зависимости от косинуса гиперболического.

Рассмотрим
теперь случай, когда кривая, длину
которой необходимо вычислить, задана
параметрически, то есть при
этом изменение от до приводит
к изменениюот до .
Пусть функции и непрерывны
вместе со своими производными на
отрезке и
при этом .
Тогда ,
а .
Подставим значение данной производной
и дифференциала в формулу для длины
дуги в прямоугольной системе координат
(п. 5):

.

В
случае пространственной кривой ее
параметрическое задание будет выглядеть
следующим образом:

Если
указанные функции непрерывны вместе
со своими производными на отрезке ,
то можно доказать, что длина данной
кривой вычисляется по формуле

.

7. Длина дуги в полярной системе координат

Если
кривая задана в полярной системе
координат, то она описывается функцией ,
где .
Пусть непрерывна
вместе со своей производной на отрезке .

Перейдем
от полярной к прямоугольной системе
координат: .
Но так как ,
то получаем, что .
Иначе говоря, и выражены
через параметр ,
поэтому можно воспользоваться формулой
для длины дуги при ее параметрическом
задании (п. 6.):

Возведя
в квадрат выражения в скобках и выполнив
элементарные преобразования, получаем:

.

Обычно
данную формулу записывают следующим
образом:

.

31. http://phys.rsu.ru/web/students/1/MatAnDetInt2.pdf

http://www.kakprosto.ru/kak-125630-kak-vychislit-dlinu-krivoy

Соседние файлы в папке билеты

• #
• #

Длина дуги кривой