Как найти длину дуги меридиана

Планирование экспедиции. Геодезия и отвага

Это продолжение истории Экваториальной Градусной экспедиции в XVIII веке отправившейся к, как следует из названия, экватору, чтобы уточнить форму Земли. 

Нашу научную экспедицию к берегам Перу мы оставили в том месте, где морской министр Франции, выделивший государственный бюджет на проект, пришел в ужас от кадровой политики ученых и сам занялся подбором персонала, выделением кредитов и денег, а также дипломатической перепиской с испанским двором. Луи Годену, как идеологу, оставалось лишь позаботиться о плане работ и инструментах.

Планирование работ

Планирование работ происходило в публичном пространстве кофеен и трактиров, широко обсуждалось в уже упомянутом нами Градо и в личной переписке всей ученой братии. Над чашками и бокалами разворачивались карты (довольно устаревшие) и шли ожесточенные споры.

Луи Годен, руководитель, ослепленный легким успехом, заявляет о том, что лучше измерить длину не 1 градуса меридиана (около 111 км), а целых четырех. Определенный смысл в этом действительно есть: чем большее расстояние мы измеряем, тем больше мы в безопасности от влияния случайных погрешностей. Но четыре градуса! Почти четыре с половиной сотни километров в малоизученном высокогорье, на которое и карт-то толком нет!

В чем заключалась задача экспедиции? Требовалось измерить длину дуги меридиана в 1 градус на экваторе и сравнить, на сколько туазов (это местная мера длины) она отличается от 1 градуса Парижского меридиана.

На злобу дня в Академию пришло едкое письмо из России, где в самом вежливом тоне Жозеф Делилль, создатель Санкт-Петербургской обсерватории, предложил коллеге не мелочиться и, чего уж, измерить дугу меридиана до самой Огненной Земли. Чтобы дважды не ходить. Впрочем, Делилль имел право быть сколько угодно резким: Годен был его учеником.

Маленькая историческая справка

В 1735 году, о котором мы говорим, в России царствовала Анна Иоанновна, племянница Петра I: Екатерина I уже умерла, а ее дочь Елизавета еще не захватила престол. Кстати, если вы окажетесь в Москве, сходите поглядеть на Царь-колокол. Когда Луи Годен готовил свою экспедицию, Царь-колокол отливали в Кремле в специально подготовленной яме. А в Академии Наук Петербурга за астрономию отвечал Жозеф Николя Делилль, приглашенный из Парижа еще Петром I.

Делилль совершенно легендарный дядька. Учился он у Джованни Кассини, итальянца, стоявшего во главе первой обсерватории Парижа. Потом уехал в Россию делать обсерваторию в Петербурге. Тогда она размещалась в здании Кунсткамеры. Он закупил приборы, написал план обучения молодых астрономов, организовал регулярные метеоизмерения, предложил основать службу времени. Кстати, в Кунсткамере в экспозиции “Первая обсерватория” демонстируются те самые заказанные им инструменты. По предложению Делилля, при Академии Наук был создан Географический департамент для руководства картографированием. Страна большая, карты на эту огромную территорию надо создавать, а существующие – обновлять. Более того, Делилль придумал коническую проекцию, как раз для нашей территории подходящую.

Про проекции хочу немного пояснить

Помните старую шутку:

Никто не сделал больше для величия России, чем проекция Меркатора.

Судя по общественному резонансу, слишком многие приняли изящный юмор за чистую монету. Дело в том, что нельзя просто так взять и перенести (земной) шар (мы же еще про XVIII век) на плоскость.

Выше картинка цилиндрической проекции Меркатора Проекция – это математический способ перенести изображение с земного шара на плоскую карту с контролируемым искажением углов и расстояний. Идея проста: земной шар мы оборачиваем бумажным цилиндром, и в месте соприкосновения (это может быть экватор, как на картинке, или меридиан) длина линии (например, дороги) на шаре будет равна длине линии на бумаге. Чем дальше от места касания – тем больше при переносе на бумагу будут искажены длины линий. Поперечная проекция Меркатора (когда цилиндр касается Земного шара по меридиану) – сегодня самая популярная из проекций.

Россия, однако, далеко от экватора и вытянута с востока на запад. Получаются сплошные искажения. Поэтому Делилль в своем XVIII веке придумал специальный подвид конической проекции.

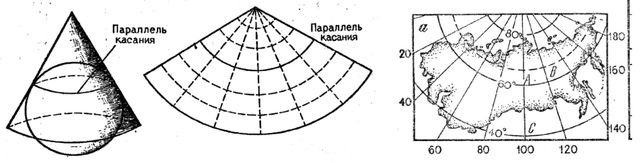
Тут земной шар оборачивается конусом, а значит “соприкосновение” бумаги с шаром идет по параллели. Профит: меньше искажений на нашу большую территорию.

Почему Делилль молодец и про проекции надо помнить? Во-первых, до конца ХХ века по бумажным картам выполняли измерения: определяли длины и площади. И подготовка любого путешествия велась по картам. Не учел искажение – не заложил денег и провианта – погиб в пути. Сейчас проекции тоже существуют, хотя обычный пользователь редко сталкивается с ними напрямую. А вот косвенно – еще как. Дело в том, что координаты, которые измеряет GPS-приемник (при обмере приусадебного участка, для постановки на учет, например) – пространственные и относятся к тому самому Земному шару (на самом деле, эллипсоиду). А координаты, которые фигурируют в документах на собственность – плоские. Относящиеся к поперечно цилиндрической проекции шара на плоскость. И, чтобы пересчитать одно в другое, надо не только помнить о том, что пересчет необходим, но и помнить, с какой точностью выведены те формулы, которые заложены в программу пересчета.

Кстати, Делилль тоже пытался заниматься градусными измерениями: года через два после Луи Годена. Но ему сократили финансирование, поскольку для нашей страны эта сугубо научная (как тогда казалось) задача не была первостепенной. Увы, карьера ученого в Петербурге завершилась бесславно. Он оказался замешан в шпионском скандале (то ли правда было за что, а то ли политическая борьба за место директора обсерватории) и вернулся в Париж к 1747 году. Зато в России весь XVIII век для измерения температуры использовали градусы Делилля. Но вернемся к основному повествованию.

Как измерить длину дуги меридиана?

Что именно собирались делать ученые, когда доберутся до тайного города Кито, что в Перу? Помните, мы уже говорили об Эратосфене и градусных измерениях? Градусные измерения – это когда между двумя точками, расположенными на одном меридиане, измеряют расстояние и разность широт.

Про измерение расстояния: к XVIII веку (и, кстати, до конца века двадцатого) для этой цели применялся метод триангуляции. Как следует из названия – она имеет отношение к треугольникам.

Как триангуляция появилась в геодезии?

Был такой голландский ученый, живший в XVI веке, Эратосфен Батавский (в те времена было принято брать себе хвастливые прозвища, подражая ученым древности), он же Виллеборд Снелл. Именно он использовал и популяризировал известную из математики триангуляцию для геодезических работ.

Подобно Эратосфену, Снелл тоже выполнял градусные измерения для определения радиуса Земли. Ему тоже нужно было найти длину дуги меридиана в градусах и в линейной мере (милях, к примеру). Однако караванов с погонщиками в северной Европе не было, так что расстояние пришлось определять самостоятельно.

Как устроена триангуляция?

Предположим, мы хотим найти расстояние между весьма удаленными точками (допустим удаленных на 100 километров). Просто измерить это расстояние невозможно: нет прямой видимости, нет возможности хотя бы построить прямую линию между точками (ведь одна может находиться на холме а другая на низменности, между ними могут быть реки, овраги и озера. На помощь приходит цепочка треугольников.

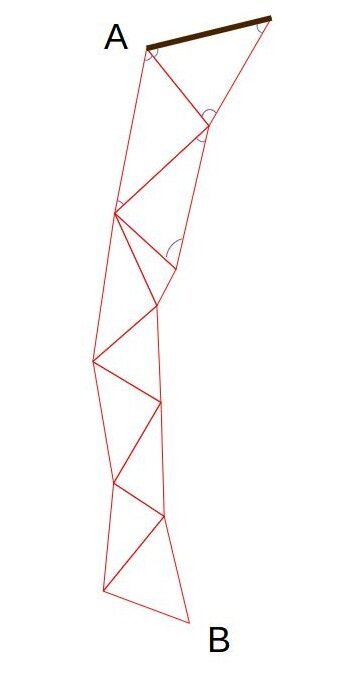
Допустим, нам нужно найти расстояние (АВ). Мы строим цепочку стыкующихся треугольников вокруг этой линии и измеряем небольшую (до 10 км) сторону треугольника A-1.

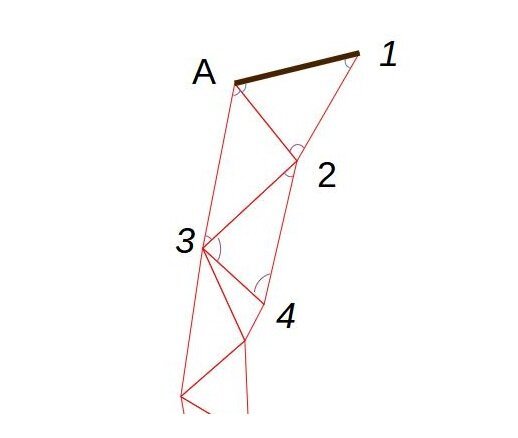
Измеренная сторона на рисунке помечена коричневым. Дальше мы угломерным прибором (квадрантом, астролябией, тахеометром) измеряем все внутренние углы треугольника 1-А-2. Получается, нам известны одна сторона и углы в треугольнике. Значит мы можем вычислить оставшиеся стороны в треугольнике. Среди прочего – мы найдем сторону А-2. И, если мы измерим все углы в треугольнике А-2-3, то сможем найти все стороны и для него тоже. Таким образом, последовательно решая стыкующиеся треугольники, для которых известны внутренние углы, мы сможем отыскать длины сторон всех треугольников.

Тут возникает нестыковка: мы можем отыскать все элементы треугольника по стороне и всего лишь двум углам. Значит, измерять все углы нет необходимости, достаточно измерить только два из трех? Теоретически это так. Однако на практике измеряют третий угол, чтобы обеспечить избыточность измерений. Как минимум – это такой простейший контроль: если сумма всех углов не будет равна 180 градусам – где-то в измерения вкралась серьезная ошибка.
Существуют статистические методы (курс ТМОГИ), позволяющие оценить погрешность, с которой были выполнены измерения и вычисления окончательной величины (расстояния), но в первой трети XVIII века, о которой я рассказываю, про все это имелись скорее смутные догадки.

Примерно по такой схеме, как описана выше, строил свои рассуждения Снелл. Он измерил расстояние от своего дома до шпиля местной церкви, а затем построил цепочку стыкующихся треугольников (триангуляции), которая позволила ему определить расстояние между городами Алкмар и Берген-оп-Зом, которые лежат на одном меридиане. Далее, зная длину дуги меридиана в линейной мере (милях) и в градусной мере – он мог вычислить радиус Земли, подобно Эратосфену (настоящему Эратосфену, Киренскому).

Метод Снелла оказался удачным, выполнимым и был взят на вооружение. Разумеется, по мере применения он совершенствовался: измерения выйдут точнее, если треугольники будут, по возможности, равносторонние или хотя бы равнобедренные. Придумали также делать дополнительный базис (измерять еще одну сторону треугольника где-то в конце цепочки) – для контроля. Эта сторона треугольника будет известна из измерений и из вычислений. Разница поможет оценить погрешность, с которой проводились работы.

Кстати, триангуляция была основным методом высокоточных геодезических измерений до самого конца XX века, пока не появились спутниковые системы позиционирования, GPS/ГЛОНАСС. Но это уже – совсем другая история.

Вернемся к Экваториальной экспедиции 1735 года. Что именно предстояло сделать ученым?

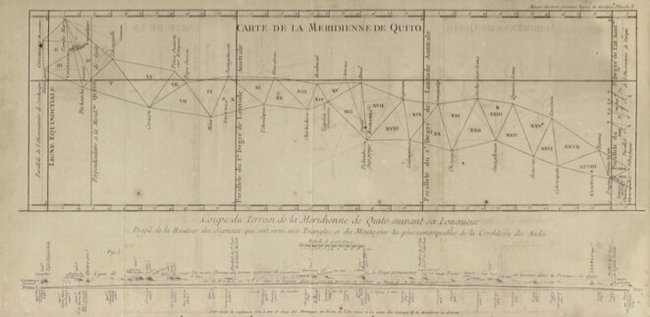
Ученые решают разбить вдоль меридиана (с севера на юг) цепочку треугольников. Треугольники требуется делать по возможности равносторонними или хотя бы равнобедренными, на местности необходимо обеспечить видимость хотя бы на две соседние вершины. Учитывая расстояния и сложности местного рельефа, треугольников по плану двадцать семь. Длина стороны в них около 30-40 км.

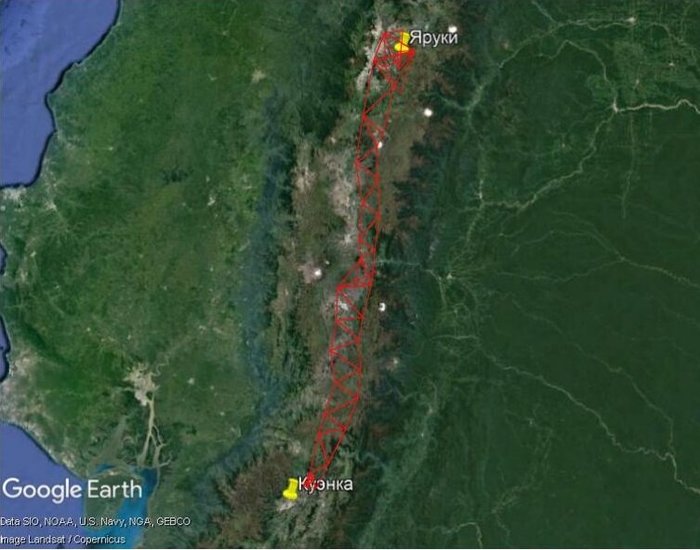
Измерена будет сторона одного из северных треугольников (базис в районе Яруки) и еще одна сторона на юге (базис в Куэнке), для контроля результатов. К сожалению, ввиду того, что это горная цепь с ущельями, скалами, реками и провалами, удобное плато для базиса было найти трудно, поэтому его длина существенно меньше (раза в четыре), чем длины сторон основных треугольников. Базис составит около 12 км. Во всех прочих треугольниках будут измерены внутренние углы. После этого ученые последовательно вычислят длины сторон всех треугольников.

Казалось бы: как теперь из наклонных сторон треугольников получить длину меридиана? Ученые будут вычислять длину проекции каждой западной стороны треугольника на меридиан. В сумме они дадут длину дуги меридиана:

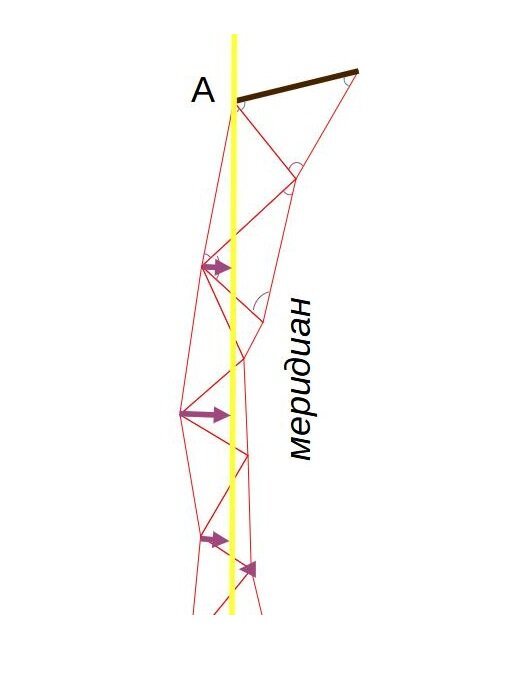
Кстати, вот любопытный факт про измеряемую сторону треугольника (базис, как он называется в триангуляции):

Деллиль в России (и еще кое-то из его коллег в Швеции) считал, что удобно будет измерять базис по замерзшему льду реки или залива, поскольку он образует ровную, поверхность с идеальной видимостью. Очень крутая и новаторская по тем временам мысль. Увы, замерзающих заливов в Перу не было.

Тот план, который Годен изначально представил в Академии, касался измерений в горной долине между западной и восточной цепью Анд. Это казалось разумным: горные вершины послужат отличным ориентиром для наблюдений, а города Кито (на севере) и Куэнка (на юге), упомянутые на карте, должны иметь хоть какие-то подъездные дороги. Однако потом Годен увлекся идеей измерять не меридиан, а параллель, его коллеги вообще хотели держаться ближе к побережью, так что планирование миссии застопорилось и окончательный ответ на вопрос “а что именно мы там будем делать?” не был дан до самого отплытия из Франции.

В защиту такого подхода руководителя миссии следует сказать, что предварительная подготовка работ велась по очень приблизительным картам, самой свежей из которых было лет двадцать. Последним французом, побывавшим в Перу был Амеде Франсуа Фрезье (торговец, инженер и шпион).

Любопытно, что широко известен он совсем не разведдеятельностью, а клубничным десертом. Именно он привез чилийскую землянику в королевскую оранжерею. И свое французское имя fraise, ананасная земляника, ее потомок, носит по его фамилии. В общем, планирование экспедиции, хотя и было занимательным, содержало слишком много белых пятен. Все станет понятно на местности. А пока следовало позаботиться об инструментах.

Все статьи этого цикла:

1. О форме Земли: тыква или дыня?

2. Как набрать команду к экватору?

3. Планирование экспедиции.

4. Приборы и инструменты.

5. Дорога на Запад.

6. Базисные измерения и политика.

7. Триангуляция и коррида.

8. О звездном непостоянстве.

9. Нельзя просто так взять и вернуться из экспедиции.

Пусть точка А
(рис. 11.1) на меридианном эллипсе имеет
широту В.
Возьмем на бесконечно малом расстоянии
ds
от точки А
точку А₁,
имеющую широту B+dB;
таким образом, разность широт точек А
и А₁
,соответствующая дуге меридиана ds,
будет dB.

Рис.
11.1

Рассматривая
элементарную дугу ds
как дугу окружности с радиусом M,
будем иметь:

ds
= MdB,

или

.

Длина дуги меридиана
между точками, имеющими широты В₁
и В₂,
выразится так:

.
(11.1)

Таким образом,
вычисление длины дуги меридиана сводится
к нахождению эллиптического интеграла
вида

,

который, как
известно, в элементарных функциях не
интегрируется.

Для вычисления
указанного интеграла разложим
подинтегральную функцию

в ряд по биному Ньютона, после чего
почленно произведем интегрирование,
удерживая необходимое число членов.

Разложение дает:

(11.2)

Для простоты
дальнейших выкладок ограничимся членами
с е⁴.
Четные степени синусов, входящих в
разложение функции

,
в ряд, заменим косинусами четных дуг
согласно следующим равенствам:

Теперь формула
(11.2) будет иметь вид:

(11.3)

Обозначая

(11.4),
(11.5)

Подставляя
найденное значение

в (11.1), получим:

.
(11.6)

Интегрируя
почленно, найдем:

.
(11.7)

Полученная формула
является общей для дуги меридиана.
Рассмотрим основные преобразования
формулы (11.7) в зависимости от цели ее
применения.

1.
При вычислении
геодезических таблиц,
например для вычисления таблиц координат
Гаусса, возникает необходимость вычислять
длины дуг меридианов от экватора до
точек дуги, расположенных через
определенные интервалы широты. В этом
случае начальная широта B₁
= 0. Переменной
величиной при вычислении будет широта
B₂
= В, поэтому
формула (11.7) может быть оставлена без
перегруппировки членов. Будем иметь:

(11.8)

Особенностью
этого случая является то, что широта В
может изменяться от 0
до 90°,
длина дуги значительна, и вычисления
следует вести, как правило, с большим
числом членов.

2. При обработке
градусных измерений с целью вывода
размеров земного эллипсоида
формула (11.7) становится неудобной. В
этом случае широты концов измеренных
меридианных дуг, участвующих в обработке
градусных измерений, могут считаться
постоянными; в отличие от предыдущего
случая размеры эллипсоида (или поправки
к некоторым приближенным их значениями
подлежат определению. Поэтому нужно
расположить члены ряда, выражающего
дугу меридиана, так, чтобы около
определяемых величин а,
е²,
е⁴
и т. д. сгруппировать постоянные члены.
Уравнения градусных измерений составляются
обычно по отдельным дугам длиной не
свыше 400 —
600 км, которым
соответствуют разности широт приблизительно
4 — 6°.
Так как эти дуги гораздо короче, чем
дуги, рассматриваемые в первом случае,
то число членов ряда, подлежащих
удержанию, должно быть меньше.

Преобразуем
формулу (11.7), учитывая изложенные
соображения и заменяя разности синусов
через произведения синусов и косинусов
соответствующих углов:

(11.9)

Примем:

(как стоящий при
коэффициенте с е⁴)
и введем среднюю широту дуги В_m
по формуле:

.

Получим:

(11.10)

или

(11.10΄)

Член

,
стоящий в последнем выражении, мал: даже
при s = 2000 км,
что соответствует

,
его значение будет равно

т. е. этим членом
можно пренебречь. Поэтому далее:

,

причем в последнем
выражении отброшены малые члены с е⁶
и е⁴
(B₂
– В₁)².

Делая приведение
подобных членов по возрастающим степеням
е
и выражая разность широт в секундах,
получим окончательно:

(11.11)

3. Для вычислений
в триангуляции,
когда стороны незначительны и редко
превосходят 40-50
км, дадим
более простую и удобную формулу.
Обозначим:

.

Введем вспомогательную
величину:

которая, очевидно,
представляет собою длину дуги окружности
с радиусом, равным радиусу кривизны
меридиана в точке со средней широтой
данной дуги. На основании (11.5) напишем:

Подставляем
значения коэффициентов А,
В, С:

(11.12)

Сравнивая (11.12) с
(11.10′), получим:

Полагая в поправочном
члене последней формулы a(1
— е²)
=M_m,
т. е. пренебрегая членами порядка

s
получим:

.

Окончательная
формула для вычислений в триангуляции
имеет вид:

.
(11.13)

Формула (11.13)
пригодна для расстояний до
400 км (при s
= 400 км допущенная выше погрешность
порядка

даст ошибку в значении s,
равную приблизительно 1 мм).

При s
≤
45 км значение
поправочного члена будет менее
1 мм, поэтому
поправочный член в (11.13) можно отбросить
и вычисления вести по формуле:

(11.14)

Следовательно,
при длине дуги, меньшей 45 км, ее можно
рассматривать как сферическую с
центральным углом, равным разности
широт ее конечных точек, и описанную
радиусом меридианного сечения,
соответствующим средней широте дуги.

На основании
формулы (11.14) можно решить обратную
задачу: зная длину дуги и среднюю широту
ее, определить разность широт конечных
точек
дуги:

.

(11.15)

Практически
нередко приходится решать следующую
задачу. Даны
широта первой точки В₁,
расстояние по дуге меридиана до второй
точки s;
требуется определить широту второй
точки В₂.
Имеем:

B₂=B₁
+
(B₂
–
B₁).

Для определения
(B₂
–
B₁)
воспользуемся
формулой (11.15); однако сразу по этой
формуле искомая разность (B₂
–
B₁)
вычислена
быть не может, так как неизвестна средняя
широта В_m,
по которой должен быть рассчитан радиус
М
или взята из таблиц величина [1]_m
. Рассмотрим решение задачи с применением
метода последовательных приближений.

В первом приближении
вычисляют (B₂
–
B₁),
используя для определения [1]
широту первой точки, и получают
приближенное значение

(B₂
–
B₁)₁
= s[1]₁,

и далее

(B₂)₁
=
B₁
+ (В₂—
В₁)₁.

С этим значением
широты второй точки вычисляют приближенно
среднюю широту

,
используя найденную приближенную
среднюю широту (В_m)₁,
находят разность широт (B₂
— B₁)₂
и среднюю широту (В_m)₂
во втором приближении; далее, аналогично
производят вычисления в третьем
приближении, четвертом и т. д. до тех
пор, пока два смежных приближения не
дадут одинаковые результаты в пределах
заданной точности, которые и будут
окончательными.

При вычислении
длин дуг свыше
45 км формулу
(11.13) употребляют в
логарифмическом виде:

.
(11.16)

Известно, что

,

где х
— малая величина, меньшая единицы, а μ
— переходный модуль от натуральных
логарифмов к десятичным.

Применяя это
разложение к выражению (11.16), получим
формулу для вычисления с помощью
восьмизначных таблиц логарифмов:

.
(11.17)

Используя прежние
обозначения и, кроме того, обозначая

,

получим окончательно:

,
(11.18)

причем последний
член уравнения (11.18) выражен в единицах
8-го десятичного знака логарифма.

Коэффициенты А,
В, С,
которые были, введены ранее при выводе
формул для дуги меридиана, для эллипсоида
Красовского имеют следующие значения:

А =
1,005 051 7739,

В =
0,005 062 37764,

С
= 0,000 010 62451,

D
= 0,000 000 02081.

В табл. 1 приведены
для справок длины дуг меридиана на
эллипсоиде Красовского для некоторых
широт с точностью до 0,1 м.

Таблица 1

B	Длина дуги меридиана (м)
В один градус	В одну минуту	В одну секунду
0°	110 576,3	1842,9	30,7
30°	110 854,4	1847,6	30,8
60°	111 414,1	1856,9	30,9
90°	111 695,8	1861,6	31,0

П р и м е р 1.
Вычислить длину дуги меридиана между
двумя его точками (s
> 45 км),
широты которых равны В₁
= 46°59’10”,315;
В₂
= 48°54’36”,482.

Вычисления
производим по формуле (11.18), т. е.

,

по следующей схеме:

B2	48°54’36”,482 lg(B2 – B1)΄΄	3.8404 9296
B1	46°59’10”,315 lg[1]m	8.5102 3202
B2 – B1	1°55‘26”,167 lgs΄	5.3302 6094
(B2 – B1)΄΄	6926”,167 Δ lgs	-4
Bm	47°56‘53”,4 lgs	5.3302 6090
2Bm	95°53‘47” s	213 924,685 м
lgk	3.932-10 lgμ	9.638-10
lg(B2 – B1)΄΄2	7.681 lg108	8.000-10
lg cos2Bm	9.012-10 lg e2	7.826-10
	доп. lg8	9.097-10
lgΔ lgs	0.624-10 доп. lgρ΄΄2	9.371-20
Δ lgs	– 4.2 lg k	3.932-10

Для контроля длина
той же дуги может быть вычислена по
таблицам для
вычисления
координат Гаусса.
В таблицах приводятся длины дуг меридианов
от экватора -до заданных точек через
одну
минуту.

Искомая длина
дуги меридиана в определится как разность
дуг меридианов
х₂
и х₁
от экватора
до точек с широтами В₂
и В₁.
Указания
о порядке вычислений
дуг
приведены во введении к упомянутым
таблицам.

Если длина дуги
s
≤ 45
км, то, как
следует из формулы (11.14),
вычисление
ведется
по схеме
примера
в его первом и втором столбцах, но без
вычислений поправочного члена.

П
р
и
м
е
р
2.
Вычислить широту В₂
точки 2,
если известна широта В₁
точки 1
и
расстояние s
между
этими точками, лежащими на одном меридиане
(точка 2—севернее
точки 1).

lg
s
= 4.494 2945,
В₁
= 57°24’49”,218.

Задача решается
методом приближений.

1-е приближение

lg s	4.49 429
lg[1]1	8.50 954
lg b”	3.00 383
b	+16‘48”,8
B1	57°24’49”,2
B‘2	57°41‘37”,0

2-е
приближение

B1	57°24’49”,2
½ b	+8.24,4
B΄m	57°33‘13”,6
lg s	4.494 2945
lg[1]m	8.509 5279
lg b”	3.003 8224
b	16‘48”,840
B1	57°24’49”,218
b	+16‘48”,840
B”2	57°41‘38”,058

3-е приближение

B1	57°24’49”,218
½ b	+8.24,420
Bm	57°33‘13”,638

Так как величина
[1]_m,

соответствующая значению широты В_m
полученной для решения задачи в третьем
приближении, будет иметь то же значение,
что и во втором, то в продолжении
вычислений необходимости нет. Искомое
значение широты для точки 2
будет В₂
= 57°41′38”,058.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  05.09.2019181.25 Кб3Л1.doc

• #
• #

  05.09.2019249.34 Кб6Л2.doc

• #
• #

  05.09.2019454.66 Кб10Л3.doc

• #
• #

  05.09.2019179.71 Кб11Л4.doc

• #
• #
• #

1. Каким образом греческий учёный Эратосфен определил размеры Земли?

Идея Эратосфена заключается в следующем. На одном и том же географическом меридиане земного шара выберем две точки $O_1$ и $O_2.$ Обозначим длину пути меридиана $O_1O_2$ через $l,$ а её угловое значение через $n$ (в градусах). Тогда длина пути $1°$ меридиана $l_0$ будет равна:

$$l_0=dfrac{l}{n},$$

а длина всей окружности меридиана:

$$L=360°·l_0=dfrac{360°·l}{n}=2pi R,$$

где $R$ — радиус земного шара. Отсюда $R=dfrac{180°·l}{pi n}.$

2. Как определяют длину дуги меридиана триангуляционным методом?

Длина дуги определяется путём вычислений, требующих измерения только сравнительно небольшого расстояния — базиса и ряда углов. По обе стороны дуги $O_1O_2$, длину которой необходимо определить, выбирается несколько точек $A, B, C, …$ на взаимных расстояниях до 50 км с таким расчётом, чтобы из каждой из них были видны по меньшей мере две другие точки.

Длину базиса очень тщательно измеряют специальными мерными лентами. Измеренные углы в треугольниках и длина базиса позволяют по тригонометрическим формулам вычислить стороны треугольников, а по ним — длину дуги $О_1О_2$ с учётом её кривизны.

3. Что понимают под горизонтальным параллаксом?

Определение расстояний до тел Солнечной ситсемы основано на измерении их горизонтальных параллаксов. Горизонтальный параллакс — угол $p,$ под которым со светила виден радиус Земли, перпендикулярный к лучу зрения.

4. Как определить расстояние до светила, зная его горизонтальный параллакс?

Зная горизонтальный параллакс светила, можно определить его расстояние $D.$ Расстояние до светила $D=S=dfrac{R_⊕}{sin p},$ где $R_⊕$ — радиус Земли. Приняв $R_⊕$ за единицу, можно выразить расстояние до светила в земных радиусах.

5. Что такое астрономическая единица?

Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а.е.), которая равна среднему расстоянию Земли от Солнца(1 а.е. ≈ 149 600 000 км).

6. В чём состоит радиолокационный метод определения расстояний до небесных тел?

Расстояние до объекта по времени прохождения радиолакационного сигнала можно определить по формуле $S=dfrac{1}{2}ct,$ где $S$ — расстояние до объекта; $c$ — скорость светы; $t$ — время прохождения сигнала до объекта и обратно.

7. на каком расстоянии от Земли находится небесное тело, если его горизонтальный параллакс равен 1′?

Для нахождения расстояния применим формулу:

$$D=dfrac{206265”}{p”}R_⊕.$$

Приняв радиус Земли $6371, км,$ получим $D=1, 314, 114, 315, км,$ или $8.8, а.е.$

8. Определите линейный радиус Луны, если во время наблюдений стало известно, что её горизонтальный параллакс в это время равен 57′ а угловой радиус — 15,5′ Радиус Земли принять равным 6400 км.

Дано:

$p = 57′,$
$ρ = 15.5′,$
$R_З = 6400, км.$

$R – ?$

Решение:

Найдём расстояние $D$ до Луны:

$D=dfrac{R_З}{sin p};$ $D=dfrac{6400}{sin 0.95°} approx 3.86 · 10^5, км.$

Вычислим линейный радиус:

$R=D·sin ρ;$ $R = 3.86 · 10^5 · sin 0.26° approx 1752, км.$

Ответ: $1752, км.$

9. Определите диаметр Меркурия, если при прохождении по диску Солнца его угловой диаметр оказался 11.0″, а горизонтальный параллакс в этот момент равен 14.3″.

Дано:

φ=28°.varphi=28°.

Найти:

aМ−?a_М-?

Решение:

sin⁡φ=aМaЗ.sin varphi=dfrac{a_М}{a_З}.

aМ=a⊕⋅sin⁡(28°)=0.4694…≈=0.47 а. е.a_М=a_opluscdot sin(28°)=0.4694…approx=0.47text{ а. е.}

Ответ: aМ=0.47 а. е.a_М=0.47text{ а. е.}

Присоединяйтесь к Telegram-группе @superresheba_11,
делитесь своими решениями и пользуйтесь материалами, которые присылают другие участники группы!

Содержание

• – Чему равна длина одного градуса параллели?
• – Какая длина 1 градуса меридиана в КМ?
• – Чему равен один градус меридиана?
• – Какое расстояние между меридианами?
• – Как определить длину дуги одного градуса параллели?
• – Как найти длину 1 градуса?
• – Сколько градусов в 1 км?
• – Какую длину имеет любой меридиан Земли?
• – Чему равна длина экватора Земли?
• – Сколько километров в градусе широты и долготы?
• – Какие бывают параллели?
• – Кто ввел понятие широта и долгота?
• – Как рассчитать длину дуги меридиана?
• – Как рассчитать длину параллели по градусной сети?
• – Как найти длину параллели по градусной сети?

На глобусе и картах параллели обычно отмечаются с промежутками десять или пятнадцать градусов, стартуя от ноля на Экваторе и заканчиваются на Северном (+ 90°) и Южном (- 90°) полюсах.

Чему равна длина одного градуса параллели?

Длина дуги параллели в 1°, 1′ и 1″ по долготе (по линии запад-восток), метров

Широта, градус	Длина дуги параллели в 1° по долготе, м	Длина дуги паралл в 1′,м
1	111305	1855
2	111254	1854
3	111170	1853
4	111052	1851

Какая длина 1 градуса меридиана в КМ?

Расстояние между двумя параллелями (фактически — дуга меридиана), которые отличаются на 1° по широте, — примерно 111 км.

Чему равен один градус меридиана?

Меридианы можно провести через любые точки земного шара. Все они пересекаются в точках полюсов и ориентированы с севера на юг. Средняя длина дуги 1º меридиана 40008,5 км : 360° = 111 км . Направление местного меридиана в любом пункте можно определить в полдень по направлению тени от гномона или другого предмета.

Какое расстояние между меридианами?

Линии долготы – меридианы, пересекающие параллели под прямыми углами и сходящиеся у полюсов, тоже подразделяются на градусы и минуты. Только на экваторе расстояние в 1° между соседними меридианами равно расстоянию между соседними параллелями – 111 км (69 уставных миль).

Как определить длину дуги одного градуса параллели?

Для определения длины одного градуса дуги произвольной параллели нужно умножить 111,3 км (длину дуги экваториальной параллели в 1 градус) на косинус угла, соответствующего искомой параллели.

Как найти длину 1 градуса?

Чтобы рассчитать длину 1° меридиана,нужно окружность земли разделить на количество градусов: 40 000 км: 360°=111 км.

Сколько градусов в 1 км?

Тут все просто: длина окружности (меридиана) постоянна – 40 008,55 км, разделим на 360°, получим: 111,134861111 км в одном градусе, делим на 60 минут: 1,85224768519 км в одной минуте, делим на 60 секунд: 0,0308707947531 км (30,8707947531 м) в одной секунде.

Какую длину имеет любой меридиан Земли?

Длина каждого меридиана на общеземном эллипсоиде равна 20 004 274 м. Все точки одного меридиана имеют одинаковую долготу, но разную широту.

Чему равна длина экватора Земли?

Оба определения приводят к длине экватора 40 075 км с разницей во второй значащей цифре после запятой, отражающей реально существующую неопределённость (±2 м) в определении усреднённого радиуса Земли.

Сколько километров в градусе широты и долготы?

Географическая миля определяется как длина одной минуты дуги вдоль экватора, поэтому длина градуса долготы вдоль экватора составляет ровно 60 географических миль или 111,3 километра.

Какие бывают параллели?

В географии выделяют 5 основных параллелей:

• Экватор;
• Северный тропик (тропик Рака);
• Южный тропик (тропик Козерога);
• Северный полярный круг;
• Южный полярный круг.

15 авг. 2019 г.

Кто ввел понятие широта и долгота?

13 октября 1884 года на Международной меридианной конференции в качестве нулевого был выбран Гринвичский меридиан. Понятия широты и долготы ввел греческий ученый Эратосфен, а Птолемей впервые использовал нулевой меридиан в карте мира в своем сочинении «География».

Как рассчитать длину дуги меридиана?

Длина дуги меридиана и параллели

Если необходимо вычислить длину дуги меридиана ΔХ =Х2-Х1 , заключенную между двумя точками с широтами, соответственно В2 и В1, то ее получают как разность длин дуг меридианов от экватора до этих точек.

Как рассчитать длину параллели по градусной сети?

Длина параллелей величиной 1° на разных широтах отличается. Длина увеличивается от полюсов к экватору. Длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. А = (д1+ д2) · 104,6 (длина 1° на широте 20°) = (10° + 20°) · 104,6 = 30° · 104,6 = 3 138 км.

Как найти длину параллели по градусной сети?

Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км.

Интересные материалы:

Кто поет со лонг?
Кто поёт Светка Соколова день рождения?
Кто поет ты беспощадна когда Нарядна?
Кто поет в фильме Бриллиантовая рука?
Кто поет в Иван Царевич и серый волк?
Кто поет в служебном романе У природы нет плохой погоды?
Кто поёт вместо Варлей в Кавказской пленнице?
Кто поет за Атаманшу в Бременских музыкантах?
Кто поет зацепила меня?
Кто поймал мышонка на льду?