{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.
-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
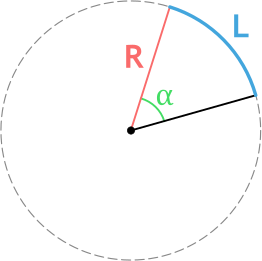
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
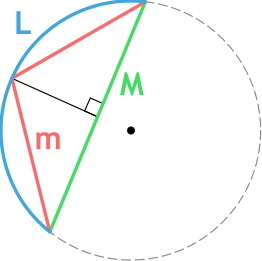
Формула длины дуги окружности по формуле Гюйгенса
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Как рассчитать длину дуги окружности
На данной странице калькулятор поможет рассчитать длину дуги окружности онлайн. Для расчета задайте радиус, угол между радиусами.
Чтобы найти длину дуги, когда не известен радиус, например, на чертеже или у предмета, то используют формулу Гюйгенса. При расчете по этой формуле есть погрешность, примерно от 0,5% до 0,02%.
Дуга окружности – это часть окружности ограниченная двумя точками.
Через радиус и угол
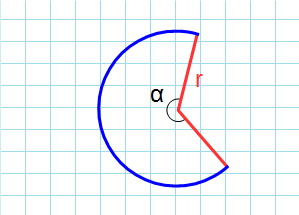
Формула для нахождения площади сектора круга:
π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.
По формуле Гюйгенса
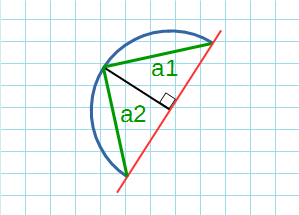
Формула Гюйгенса для нахождения длины дуги окружности:
a1, a2 – хорды.
Длина дуги
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина дуги
Чтобы найти длину дуги окружности воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна длина дуги, если:
радиус r =
угол α =
Ответ: L =
0
Округление числа π: Округление ответа:
Просто введите радиус и угол α, и получите ответ.
Теория
Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги – центральный угол α?
Формула
Если угол в градусах:
L = π ⋅ r ⋅ α ⁄ 180
Если угол в радианах:
L = r ⋅ α
Пример
Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :
L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см
См. также
-
Длина дуги
Длина дуги окружности представляет собой часть длины самой окружности, поэтому она также будет зависеть от радиуса окружности. Поскольку дуга окружности образована определенным центральным углом, то ее длина, как и площадь сектора круга, – это определенная часть исходной длины окружности, относящаяся к ней как центральный угол сектора к полному углу круга в 360°. Поэтому формула длины дуги будет выглядеть следующим образом:
Формула длины дуги окружности через диаметр образуется подстановкой вместо радиуса половины диаметра:
Также можно подставить вместо радиуса корень из произведения площади круга на число π, выведенный из формулы площади круга:
Существует также формула Гюйгенса для расчета длины дуги окружности через хорду. Для того чтобы ей воспользоваться нужно провести перпендикуляр из середины хорды, соединяющий ее с самой дугой, а из точки соединения перпендикуляра с дугой провести еще два отрезка к концам хорды. Таким образом, мы получаем два конгруэнтных перпендикулярных треугольника, гипотенузы которых мы будем использовать в формуле под обозначением l, а саму хорду назовем L. Следует учитывать, что для углов более 60 градусов формула Гюйгенса дает ощутимую погрешность в расчетах.
Длина дуги
Лариса Семеновна Петрова
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
Из этой статьи вы узнаете, как выглядит формула длины дуги окружности через угол, а также научитесь определять длину дуги сектора по формуле Гюйгенса. Также на страницу добавлены онлайн-калькуляторы для вычисления по данным формулам.
Определение 1
Дугой окружности (сектора) называют часть окружности, ограниченную двумя точками.
Чтобы определить длину дуги окружности, введите заданные данные в поля для ввода онлайн-калькулятора.
Длина дуги через радиус и угол
Для определения длины дуги можно воспользоваться формулой:
$l = π cdot R cdot frac{α}{180°}$, где
$R$ — радиус окружности;
$α$ — угол, которым характеризуется дуга;
$π$ — константа.
Рассмотрим пример на использование этой формулы.
Пример 1
Задача
Угол, ограничивающий дугу, составляет $50°$, а радиус окружности равен $9$ см. Рассчитайте, чему равна длина дуги.
Решение:
$l = 3.14 cdot 9 cdot frac{50}{180} = 7.85$ см.
Проверим длину дуги окружности с помощью онлайн-калькулятора. Результат совпадает, значит ответ верный.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Длина дуги по формуле Гюйгенса
По формуле Гюйгенса длина дуги рассчитывается следующим образом:
$l ≈ 2 cdot AB + frac13 cdot ( 2 cdot AB – AC)$, здесь
$AC$ — хорда, соединяющая концы дуги;
$AB$ — хорда, соединяющая середину дуги, расположенную в точке $B$ и конец дуги $A$.
Формула Гюйгенса не является точной. Для угла в $60°$ погрешность по этой формуле будет составлять около $0.5%$, однако для меньших значений угла погрешность уменьшается.
Также посмотрим, как использовать формулу Гюйгенса.
Пример 2
Задача
Длина хорды $AC$ равна $3.51$ см, а хорды $AB$ $2.19$ см. Чему равна длина дуги $l$?
Решение:
$l = 2 cdot 2.19 + frac13 cdot (2 cdot 2.19 — 3.51) = 4.67$ см.
Результат совпадает, а значит, ответ — верный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 27.06.2019