Как найти длину дуги определенного интеграла

При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.

Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.

Как вычислить длину кривой

Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).

Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).

Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).

Примеры:

Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

1. Точками х₀ = а, х₁…, х_n = b (х₀ < x₁ < …< х_n) разобьем отрезок [а; b] на n частей (см. рис. 183).  Пустьэтим точкам соответствуют точки М₀ = А, M₁,…,M_n =В на кривой АВ. Проведем хорды М₀M₁, M₁M₂,…, М_n-1М_n, длины которых обозначим соответственно через ΔL₁, AL₂,…, ΔL_n. Получим ломаную M₀M₁M₂ … M_n-ιM_n, длина которой равна L_n=ΔL₁ + ΔL₂+…+ ΔL_n =

2. Длину хорды (или звена ломаной) ΔL₁ можно найти по теореме Пифагора из треугольника с катетами Δx_i и Δу_i:

По теореме Лагранжа о конечном приращении функции Δу_i=ƒ'(с_i)•Δх_i, где ci є (x_i-1;x_i). Поэтому

а длина всей ломаной M₀M₁… М_n равна

3.Длина l кривой АВ, по определению, равна

.

Заметим, что при ΔL_i→0 также и Δx_i →0 ΔLi =и, следовательно, |Δx_i|<ΔL_i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx_i→ 0:

Таким образом,или в сокращенной записи l =

Если уравнение кривой АВ задано в параметрической форме

где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,

Пример 2. Определить длину окружности x² + y² = r². Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда,следовательно,

Длина всей окружности L = 2πr.

Пример 3. Найти длину дуги кривой y² = x³ от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x^1/2, откуда

Пример 4.     Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).

     Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).

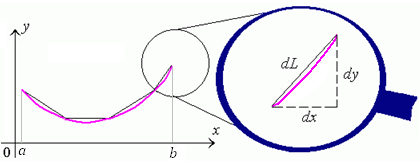
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.

      Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:

(1)

где y ‘  – производная функции y = f(x)  по переменной x.

      Длина дуги равна сумме длин составляющих ее элементов:

.

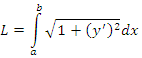Пример 5.

1. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.

Пусть
некоторая функция f(x) непрерывна на
отрезке ,
и её график на данном промежутке
представляет собой кривую или,
что то же самое, дугу
кривой :

В
предположение о непрерывности
производной  на [a,b], длина кривой AB выражается
формулой:

 или
компактнее: 

Рассмотрим
случай параметрического задания кривой:

где  t∈[a,b].
В
этом случае для определения длина
дуги  вычисляется определенный
интеграл:

Рассмотрим
случай, когда кривая задается в полярных
координатах ρ=ρ(φ) где φ∈[α,β].
Тогда для определения длины
дуги  вычисляется
следующий определенный
интеграл:

 Вычисление
объема тела вращения:

а)
если тело образовано вращением
криволинейной трапеции, ограниченной
кривой y = f(x), осью OX и двумя
прямыми x = a и x = b(a < b)
вокруг оси OX, то объем тела ;

б)
а если тело образовано вращением фигуры,
ограниченной кривой ,
прямыми y=c, y=d (c<d) и осью OY,
вокруг оси OY, то его объем ;

в)
если тело образовано вращением вокруг
оси OY фигуры, ограниченной
линией y = f (x), прямыми x = a, x = b
(0≤a≤b)  и
осью OX, то его объем можно вычислить
по формуле ;

г)
если вращается вокруг полярной оси
криволинейный сектор, ограниченный
дугой ,
двумя полярными радиусами  и ,
то  объем полученного тела может
быть вычислен по формуле .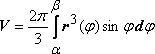

д
)вычисление объема тела по площадям
поперечных сечений

 Пусть
тело V расположено
в пространстве между плоскостями x = a и x = b,
и для  известна
площадь его поперечного сечения S = S(x).
Требуется определить объём этого тела. 

 Рассечём
это тело плоскостями x = x₀ = a, x = x₁, x = x ₂,
…, x = x_i-1, x = x_i,
…, x = x _n-1, x =x_n = b на n слоёв (a = x₀< x₁ <
< x₂<
…< x_n-1 < x_n = b),
на каждом из отрезков [x_i-1, x_i] возьмём
произвольную точку ;
будем считать, что объём слоя, заключенного
между плоскостями x = x_i-1 и x= x_i приближённо
равен объёму  цилиндрика
с площадью основания  и
высотой : .
Сумма объёмов  –
объём ступенчатой фигуры – при  стремится
к искомому объёму V,
поэтому .

Площадь
поверхности вращения.

Площадь
поверхности вращения, образующейся при
вращении вокруг оси Ox дифференцируемой
кривой, определяется по формулам (в
зависимости от способа задания)

(–
длина окружности кольца,  –
его ширина).

1. Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления

 Путь S,
пройденный телом при прямолинейном
движении со скоростью v(t) за
интервал времени от t1 до t2,
вычисляется по формуле

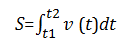
Вычисление
работы
с помощью определённого интеграла.

Пусть
под действием некоторой силы  материальная
точка М движется по прямой в направлении
оси OX.
Требуется найти работу, произведённую
силой  при
перемещении точки М из положения  в
положение .

1)     Если
сила постоянна ,
то работа выражается следующим образом .

2)     Если
сила переменная величина, то .

Теоремы
Гульдена
Выведем теоремы, связывающие площадь
поверхности (соответственно, объем
тела) вращения с центром тяжести
вращающейся дуги (соответственно,
криволинейной трапеции).

Пусть
поверхность  образована
вращением дуги ,
имеющей длину .
Мы знаем, что ордината центра тяжести
этой дуги выражается формулой

Так
как площадь поверхности вращения
выражается интегралом

то
из этого равенства следует, что .

Мы
доказали следующее утверждение,
называемое первой
теоремой Гульдина–Паппа.

Площадь
поверхности, полученной от вращения
кривой вокруг непересекающей ее оси,
равна произведению длины  дуги
этой кривой на длину окружности, описанной
центром тяжести  этой
кривой.

Аналогично,
из формулы, выражающей ординату центра
тяжести криволинейной трапеции

 и
формулы объема тела вращения 

получаем ,
т. е. следующее утверждение, называемое второй
теоремой Гульдина–Паппа:

Объем
тела, полученного от вращения плоской
фигуры вокруг непересекающей ее оси,
равен произведению площади этой фигуры
на длину окружности, описанной центром
тяжести этой фигуры.

Пользуясь
этими двумя теоремами, можно в ряде
случаев упростить процесс вычисления
поверхности или объема тела вращения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:

В более общем случае, если у нас задана функция

в декартовых координатах и стоит задача найти длину дуги этой кривой между точками

и
,
нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение

означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.