Как найти длину дуги параллели

Паралле́ль — линия сечения поверхности планеты плоскостью, параллельной плоскости экватора.

На глобусе[править | править код]

На глобусе параллель рисуется в виде окружности, все точки которой равноудалены от экватора. Все точки одной параллели имеют одинаковую широту, но различную долготу. Длины параллелей различны: они увеличиваются при приближении к экватору и уменьшаются — к полюсам. Экватор — самая длинная параллель.

На Земле[править | править код]

Длина дуги параллели в 1° по долготе[править | править код]

Чтобы найти для любой параллели длину дуги в 1°, нужно умножить 111,3 км (длину дуги экватора в 1°) на косинус угла, соответствующего географической широте искомой параллели. Например, на широтах с шагом 15° получаем:

15° — 108 км
30° — 96 км
45° — 79 км
60° — 56 км
75° — 29 км
90° — 0 км

Принято определение экватора как нулевой параллели. Северный полюс имеет широту плюс 90°, Южный полюс — минус 90°. Расстояние между двумя параллелями (фактически — дуга меридиана), которые отличаются на 1° по широте, — примерно 111 км.

Параллели (кроме экватора) не являются ортодромиями, то есть кратчайшими линиями на поверхности между любыми их двумя точками.

Основные широты[править | править код]

Существует пять основных широт, перечисленных ниже с севера на юг. Положение экватора является фиксированным (90 градусов от оси вращения Земли), но показатели других широт зависят от наклона оси относительно плоскости орбиты Земли, и поэтому не являются идеально фиксированными. Приведённые ниже значения даны на 20 сентября 2020^[1]:

• Северный полярный круг — 66°33′48,0″ с. ш.
• Северный тропик (Тропик Рака) — 23°26′12,0″ с. ш.
• Экватор — 0° широты
• Южный тропик (Тропик Козерога) — 23°26′12,0″ ю. ш.
• Южный полярный круг — 66°33′48,0″ ю. ш.

Эти широты, за исключением экватора, отмечают различия между пятью основными географическими зонами.

Параллели как государственные и административные границы[править | править код]

Параллели могут использоваться для обозначения границ между регионами или странами.

• 70° с. ш.: часть границы между канадскими территориями Нунавут (Ю) и Северо-Западные территории (С) на о. Виктория.
• 67° с. ш.: Россия, часть границы Ненецкого автономного округа (С) и Республики Коми (Ю).
• 60° с. ш.: в Канаде, граница Юкона (С) и Британской Колумбии (Ю), а также Северо-Западных территорий (C) с Британской Колумбией, Альбертой и Саскачеваном (Ю), а также материковой части Нунавута (С) с Манитобой (Ю).
• 54°40′ с. ш.: южная граница Русской Америки с 1825 г.
• 52° с. ш.: часть границы между канадскими провинциями Ньюфаундленд и Лабрадор (С) и Квебек (Ю).
• 51° с. ш.: южная граница Русской Америки с 1799 по 1821 гг.
• 49° с. ш.: бо́льшая часть протяжённости границы между Канадой (С) и США (Ю).
• 48° с. ш.: часть границы между канадскими провинциями Квебек (С) и Нью-Брансуик (Ю).
• 46° с. ш.: часть границы между американскими штатами Вашингтон (С) и Орегон (Ю),
• 46° с. ш.: Казахстан, граница Карагандинской (С) области с Туркестанской (Ю) и Жамбылской (Ю) областями.
• 45° с. ш.: часть границы между Канадой (С) и США (Ю); почти вся граница между американскими штатами Вайоминг (С) и Монтана (Ю).
• 43°30′ с. ш.: США, граница между штатами Миннесота (С) и Айова (Ю).
• 43° с. ш.: США, бо́льшая часть протяжённости границы между штатами Южная Дакота (С) и Небраска (Ю).
• 42°30′ с. ш.: США, граница между штатами Висконсин (С) и Иллинойс (Ю).
• 42° с. ш.: США, граница между штатами Орегон (С) и Калифорния (Ю); Орегон (С) и Невада (Ю); Айдахо (С) и Невада (Ю); Айдахо (С) и Юта (Ю); была установлена по северной границе Новой Испании, существовавшей в начале 19 века. Кроме того, по этой параллели проведена бо́льшая часть протяжённости границы между американскими штатами Пенсильвания (С) и Нью-Йорк (Ю).
• 41° с. ш.: США, граница между штатами Вайоминг (С) и Колорадо (Ю); часть границы между штатами Вайоминг (С) и Юта (Ю), Вайоминг (С) и Колорадо (Ю).
• 40° с. ш.: США, граница между штатами Небраска (С) и Канзас (Ю).
• 38° с. ш.: граница между зонами советской (С) и американской (Ю) оккупации Кореи с 1945 г. до начала Корейской войны (1950—1953).
• 37° с. ш.: США, граница между штатами Юта, Колорадо и Канзас (С) и Аризона, Нью-Мексико и Оклахома (Ю)
• 36° с. ш.: США, небольшая часть границы между штатами Миссури (С) и Арканзас (Ю)
• 35° с. ш.: США, граница между штатами Теннесси и Северная Каролина (С) и Миссисипи, Алабама и Джорджия (Ю).
• 33° с. ш.: США, часть границы между штатами Арканзас (С) и Луизиана (Ю).
• 32° с. ш.: США, часть границы между штатами Нью-Мексико (С) и Техас (Ю).
• 31°20′ с. ш.: часть границы между США (С) и Мексикой (Ю).
• 31° с. ш.: часть границы между Ираном (С) и Ираком (Ю).
• 31° с. ш.: США, часть границы между штатами Миссисипи (С) и Луизиана (Ю), а также между штатами Алабама (С) и Флорида (Ю).
• 28° с. ш.: Мексика, граница между штатами Нижняя Калифорния (С) и Южная Нижняя Калифорния (Ю).
• 27° с. ш.: Ливия, граница между муниципалитетами Эль-Вахат (С) и Эль-Куфра (Ю).
• 26° с. ш.: часть границы между Западной Сахарой (С) и Мавританией (Ю).
• 25° с. ш.: часть границы между Мавританией (С) и Мали (Ю).
• 22° с. ш.: бо́льшая часть границы между Египтом (С) и Суданом (Ю).
• 20° с. ш.: небольшая часть границы между Ливией (С) и Суданом (Ю).
• 20° с. ш.: Судан, граница между штатами Северный (С) и Северный Дарфур (Ю).
• 19° с. ш.: Мавритания, граница между областями Иншири и Адрар (С) и Трарза (Ю).
• 17° с. ш.: граница с демилитаризованной зоной между бывшими Демократической Республикой Вьетнам и Южным Вьетнамом до начала Вьетнамской войны.
• 15°30′ с. ш.: часть границы между Мавританией (С) и Мали (Ю).
• 1° ю. ш.: часть границы между Угандой (С) и Танзанией (Ю).
• 5° ю. ш.: Демократическая Республика Конго: часть границ между провинциями Маниема и Южное Киву (С) и Ломами и Танганьика (Ю)
• 8° ю. ш.: Папуа — Новая Гвинея, граница между регионами Момасе (С) и Папуа (Ю).
• 13° ю. ш.: часть границы между Анголой и Замбией
• 21° ю. ш.: Ботсвана, граница между округами Северо-Западный (С) и Ганзи (Ю).
• 21° ю. ш.: Боливия, часть границы между департаментами Чукисака (С) и Тариха (Ю).
• 22° ю. ш.: часть границы между Намибией (С) и Ботсваной (Ю).
• 26° ю. ш.: Австралия, часть границы между Северной территорией и штатом Квинсленд (С) и штатом Южная Австралия (Ю).
• 28° ю. ш.: Аргентина, граница между провинциями Чако (С) и Санта-Фе (Ю).
• 29° ю. ш.: Австралия, часть границы между штатами Квинсленд (С) и Новый Южный Уэльс (Ю).
• 35° ю. ш.: Аргентина, граница между провинциями Кордова (С) и Ла-Пампа (Ю).
• 36° ю. ш.: Аргентина, граница между провинциями Мендоса (частично) и Сан-Луис (С) и Ла-Пампа (Ю).
• 42° ю. ш.: Аргентина, граница между провинциями Рио-Негро (С) и Чубут (Ю).
• 46° ю. ш.: Аргентина, граница между провинциями Чубут (С) и Санта-Крус (Ю).
• 52° ю. ш.: часть границы между Аргентиной (С) и Чили (Ю)

См. также[править | править код]

• Географические координаты
• 45-я Параллель (улица в Ставрополе)

Примечания[править | править код]

Ссылки[править | править код]

• U.S. Naval Observatory — mean obliquity of the ecliptic Архивная копия от 12 октября 2007 на Wayback Machine

Параллель на
эллипсоиде вращения является окружностью,
поэтому вычисление дуги параллели
сводится к определению дуги окружности
с центральным углом, равным разности
долгот конечных точек дуги.

Радиус параллели
r
определяется по формуле (9.9), которая
имеет вид:

.
(12.1)

Длина дуги параллели
s΄,
имеющей
широту В
и разность
долгот конечных точек дуги l,
очевидно,
дается формулой:

.
(12.2)

Отсюда легко
получаем разность долгот двух точек
параллели под широтой В,
расположенных на расстоянии s’,

l”
=
[2]s’
sec
B (12.3)

В табл. 3 приводятся
для справок длины дуг параллелей для
широт от 30 до 70° на эллипсоиде Красовского.

Таблица 3

В	Длина дуги параллели (м)
в один градус	в одну минуту	в одну секунду
30° 40° 50° 60° 70°	96 489,9 85 395,3 71 696,9 55 800,9 38 187,2	1608,1 1423,3 1194,9 930,0 636,5	26,8 23,7 19,9 15,5 10,6

П р и м е р.
Вычислить длину дуги параллели между
точками, лежащими на одной параллели,
если даны долготы этих точек и широта
параллели.

L₂
= 64°53’17”,358
L₁
= 62°45’14”,812
B
=
55°48’12”,382

L2 L1 l = L2 – L1 l”

64°53’17”,358 lg l” 62°45’14”,812 lg cosB 2°08’02”,546 доп lg[2] 7682″,546 lg s s

3.8855 0517 9.7497 6238 1.4912 7268 5.1265 4023 133 825,912 м

13. Вычисление площадей съемочных трапеций

Вычисление площади
съемочной трапеции или листа карты
сводится к определению части поверхности
эллипсоида, ограниченной линиями
меридианов и параллелей.

Возьмем на
эллипсоиде (рис. 13.1) два бесконечно
близко расположенных меридиана РВАР₁
и PCDP₁
с долготами
l
и 1
+ dl и
две бесконечно близко расположенные
параллели TBCR
и QADS
с широтами В
и B+dB,
пересечения которых образуют бесконечно
малую трапецию АВСD.

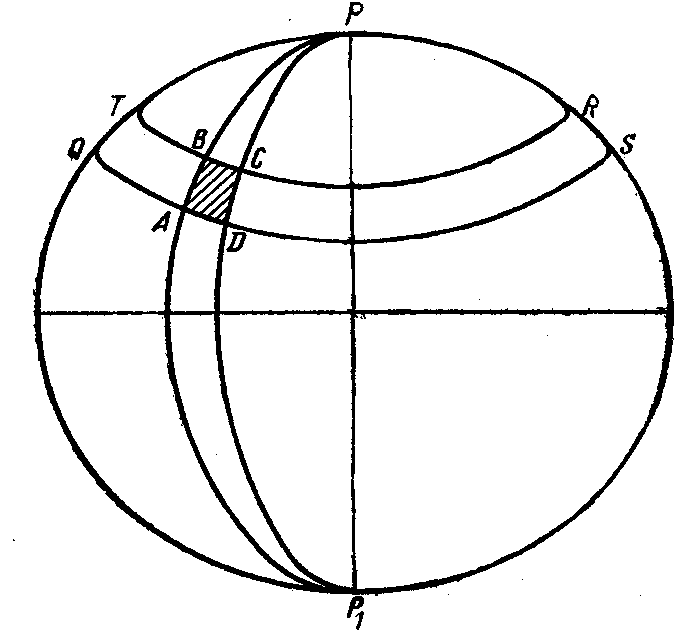
Рис.
13.1

Стороны этой
трапеции как элементы дуг меридианов
и параллелей будут равны:

AB=
CD
= М
dB,

AD
= ВС
= NcosBdl.

Площадь элементарной
трапеции ABCD
выразится формулой:

dТ
= MNcos
BdB
dl.
(13.1)

Площадь dZ
всего пояса, ограниченного указанными
параллелями, получится, если в формуле
для dT
величину
dl
заменить через 2π,
т. е

dZ
= 2π
MN cos
BdB = 2π
R²
cos
BdB,

или

.

(13.2)

Площадь поверхности
пояса эллипсоида, расположенного между
параллелями с широтами B₁
и В₂,
будет:

.
(13.3)

Для вычисления
интеграла (13.3) разложим подинтегральную
функцию в ряд по биному Ньютона (интеграл
берется и в конечном виде, однако
получаемое при этом выражение мало
пригодно для вычислений):

(13.5)

Для приведения
этой формулы к виду, удобному для
практического применения, воспользуемся
формулами, дающими выражения синусов
нечетных степеней в функции синусов
кратных дуг(эти формулы получаются на
основе общей формулы:

(13.6)

Заменяя в формуле
(13.5) синусы нечетных степеней согласно
выражениям (13.6) и подставляя пределы
интегрирования, будем иметь:

(13.7)

Заменяя разности
синусов по известным формулам
тригонометрии, получим:

При разложении
выражения (13.4) в ряд члены с е⁶,
е⁸
и т. д. не были приняты во внимание. Более
точная формула для площади пояса, с
учетом членов с е⁶,
е⁸,
будет иметь следующий вид:

Для эллипсоида
Красовского эти коэффициенты имеют
следующие численные значения:

1g А’
= 0.001 45834

1g В’
= 7.050 7767_-10

1g
C’
=4.230 14_-10

1g
D’ =
1.428_-10

(13.9)

Формула (13.8)
выражает площадь пояса эллипсоида,
ограниченного параллелями с широтами
В₁
и В₂.
Чтобы получить формулы для вычисления
площадей трапеций данного масштаба и
номенклатуры, берут разность широт
северной и южной рамок трапеций B₂
— B₁
и определяют, какую долю площади всего
пояса составляет площадь трапеции
данного масштаба, причем, очевидно, эта
доля определится в зависимости от
разности долгот меридианов западной и
восточной рамок трапеции.

Например, для
государственной карты масштаба 1:
1 000 000 B₂
— B₁
= 4°;
разность долгот восточной и западной
рамок карты Δl
= 6°, т.
е. равна 1:
60 от полной
окружности пояса. Поэтому рабочая
формула для вычисления площадей трапеции
масштаба 1: 1 000 000 будет:

(13.10)

Положив в формуле
(13.7) B₁
= 0,
B₂
= 90° и удвоив
полученное выражение, получим формулу
для вычисления площади ∑
всей
поверхности эллипсоида с удержанием
любого числа членов, так как закон
построения членов ряда совершенно ясен:

(13.11)

Рассмотрим пример
на вычисление площади трапеции масштаба
1: 100 000.

П р и м е р.
Вычислить площадь трапеции карты
масштаба 1:100
000 N-36-14.

Для площади
трапеции карты этого масштаба формула
будет иметь следующий вид:

Имеем:

B₂
=
55°40΄;
В₁
= 55°20΄;
В_m
= 55°30΄.

Вычисления
производим по следующей схеме:

1g А‘ lg sin 10° lg cos Вm lg I I

4583 7.463 7255-10 9.753 1280-10 7.218 3118-10 +0,001 653148

1g B’ lg sin 30° lg cos 3Вm lg II II

7.05 078-10 7.94 084-10 9.98 783n -10 4.97 945n -10 -0,000009538

1g C’ lg sin 50° lg cos 5Вm lg III III

4.23-10 8.16-10 9.12-10 1.51-10 +0,00000003

I -II +III k	+0,001653148 +0,000009538 +0,000000003	lg π 2 lg b доп. lg 180	0.497 1499 7.606 4857 7.744 7275-10	lg Q lg k	5.848 3631 7.220 8110-10
+0,001662689	lg Q	5.848 3631	Lg P	3.069 1741

Р
=
1172,666 кв. км.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  05.09.2019181.25 Кб3Л1.doc

• #
• #

  05.09.2019249.34 Кб6Л2.doc
• #
• #

  05.09.2019454.66 Кб10Л3.doc

• #
• #

  05.09.2019179.71 Кб11Л4.doc

• #
• #
• #

Есть у нас калькулятор, вычисляющий длину дуги меридиана в зависимости от широты, а точнее, длину дуги меридиана размером в одну минуту, более известной как морская миля. Для полноты решил написать калькулятор, рассчитывающий размер длины дуги параллели в зависимости от широты. Из достаточно очевидных соображений, чем больше широта, то есть, чем ближе мы к тому или иному полюсу, тем меньше размер дуги, скажем, в 1 градус, в метрах. Калькулятор ниже и считает размер этой дуги на заданной широте по заданному угловому размеру дуги. Для справки, на экваторе размер дуги параллели в один градус будет максимальным (широта равна нулю) и составит 111 км 319 метров (приближенно). Как это считается, описано под калькулятором.

Длина дуги параллели

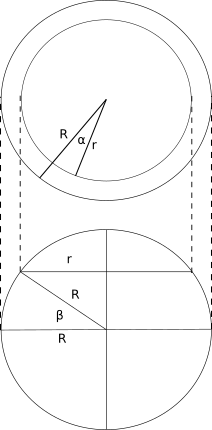
Расчет достаточно простой, и выполняется из общих геометрических соображений. Землю мы конечно приближенно представляем сферой (хотя она геоид).
Чтобы найти длину дуги окружности по углу дуги α, достаточно радиус окружности r умножить на угол дуги в радианах

Для длины дуги в 360 градусов, или 2π радиан, формула превращается в известную всем формула длины окружности

Как видно из рисунка, на определенной широте нас интересует радиус окружности r, полученной при отсечении части сферы плоскостью, параллельной плоскости экватора. На самом экваторе радиус совпадает с радиусом земли R. Выразим интересующий нас радиус через радиус Земли R и заданную широту β:

Соответственно, финальная формула

Ну и в качестве радиуса Земли берем значение, определенное в стандарте WGS-84, а именно, 6378137м. Вот и всё.

Содержание

• – Как определить расстояние в км по градусной сетке?
• – Как определить расстояние между точками в градусной мере?
• – Что можно узнать с помощью градусной сети карты?
• – Как определять по глобусу расстояние?
• – Как определить протяженность по градусной сетке?
• – Как определить расстояние в градусах по карте?
• – Как по географическим координатам определить расстояние между точками?
• – Как определить расстояние между городами с помощью координат?
• – Как посчитать расстояние между географическими координатами?
• – Как можно узнать по карте полушарий длину дуги одного градуса параллели?
• – Как ведут отсчет параллелей и меридианов?
• – Как на карте образуется градусная сетка?
• – Как определить расстояние по параллели?
• – Как на глобусе можно определить кратчайшее расстояние между двумя точками?

Длина параллелей величиной 1° на разных широтах отличается. Длина увеличивается от полюсов к экватору. Длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. А = (д1+ д2) · 104,6 (длина 1° на широте 20°) = (10° + 20°) · 104,6 = 30° · 104,6 = 3 138 км.

Как определить расстояние в км по градусной сетке?

Длина дуги одного градуса меридиана (или одного градуса на экваторе) равна 111 км.

1. Определяем расстояние между ними в градусах (из долготы одного пункта вычитаем долготу другого пункта)
2. Далее необходимо число градусов умножить на 111 км.

18 апр. 2020 г.

Как определить расстояние между точками в градусной мере?

Алгоритм определения расстояний по параллели: 1) определить значение координат двух точек параллели, расстояние между которыми необходимо рассчитать; 2) определить расстояние между двумя точками параллели в градусной мере (отсчет производится от нулевого меридиана, поэтому значения либо складываются, либо вычитаются); …

Что можно узнать с помощью градусной сети карты?

С помощью градусной сетки на глобусе и карте можно определить стороны горизонта, а также точное местоположение какого-либо объекта по его географическим координатам. Изображение меридианов и параллелей на глобусе и физической карте полушарий различно. На глобусе все меридианы — полуокружности, а параллели — окружности.

Как определять по глобусу расстояние?

Чтобы определить расстояние по глобусу надо нитью, или сантиметром, или гибкой линейкой замерить расстояние между искомыми точками на глобусе, затем полученное значение умножить на масштаб глобуса, который можно найти в районе экватора на акватории океана.

Как определить протяженность по градусной сетке?

Вычислить расстояние с помощью градусной сетки несколько сложнее. Для определения протяженности страны с севера на юг, выясните широты крайних северной и южной точек, определите разницу в градусах и умножьте полученное число на 111,1 км (градус каждого меридиана равен 111,1 км).

Как определить расстояние в градусах по карте?

Чтобы рассчитать расстояние между двумя точками на карте в градусах с севера на юг нужно знать, чему равен 1° по меридиану. Он равен 111 км. То есть находим разницу в градусах между двумя точками и умножаем её на 111 км, получаем расстояние в километрах.

Как по географическим координатам определить расстояние между точками?

Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е.

Как определить расстояние между городами с помощью координат?

Расстояние между двумя точками равно квадратному корню из суммы квадратов разностей координат по каждой оси. Каждая точка на плоскости характеризуется двумя координатами, а каждая точка в пространстве – тремя. Для того, чтобы определить расстояние между двумя точками на плоскости, надо ввести две координаты двух точек.

Как посчитать расстояние между географическими координатами?

Расстояние между пунктами, измеряемое в километрах, определяется по формуле: L = d·R, где R = 6371 км — средний радиус земного шара.

Как можно узнать по карте полушарий длину дуги одного градуса параллели?

Для определения длины одного градуса дуги произвольной параллели нужно умножить 111,3 км (длину дуги экваториальной параллели в 1 градус) на косинус угла, соответствующего искомой параллели.

Как ведут отсчет параллелей и меридианов?

По параллелям и меридианам можно определять основные и промежуточные стороны горизонта. По меридианам определяют направления «север», «юг», по параллелям – «восток», «запад». Пересекаясь, параллели и меридианы образуют градусную сеть.

Как на карте образуется градусная сетка?

Меридиан и параллель можно провести через любую точку земной поверхности. На карте и глобусе их проводят через одинаковое число градусов, например через 100или 200. Пересекаясь, они образуют градусную сетку.

Как определить расстояние по параллели?

Для определения расстояния в километрах между пунктами, лежащими на одной параллели, число градусов умножают на длину дуги 1° параллели, обозначенную на карте или определенную по таблицам.

Как на глобусе можно определить кратчайшее расстояние между двумя точками?

Как на глобусе можно определить кратчайшее расстояние между двумя точками? Большинство из них обладают меридианными дугами, которые помогают выявить географические координаты. У них есть градусные шкалы, которые помогают установить точное расположение объекта. На экваторе тоже имеется градусная шкала.

Интересные материалы:

В чем отличие клиники от больницы?
В чем отличие манки от муки?
В чем отличие маржинальности от рентабельности?
В чем отличие между желанием и мечтой?
В чем отличие общих и профессиональных компетенций?
В чем плюсы гло?
В чем плюсы не есть мясо?
В чем подавать шашлык?
В чем полезна радиация?
В чем польза баклажанов?