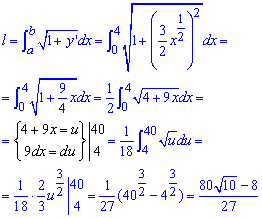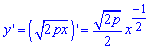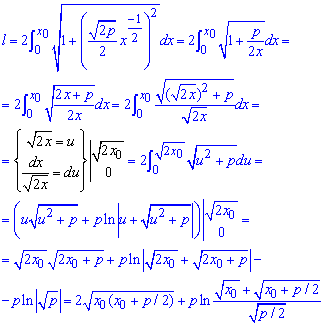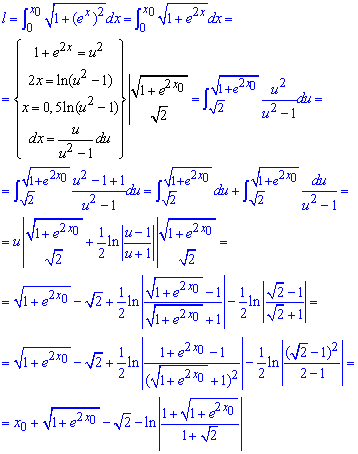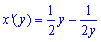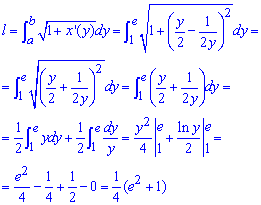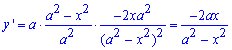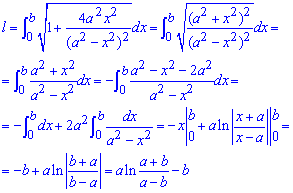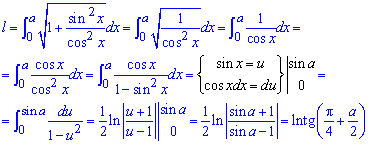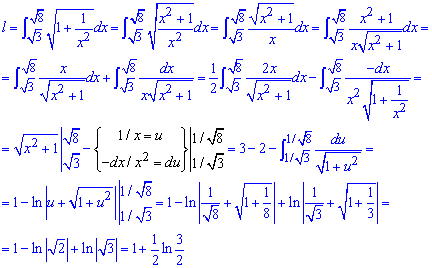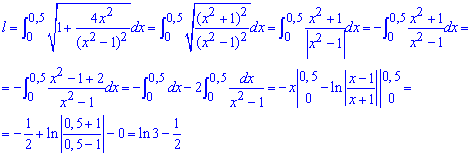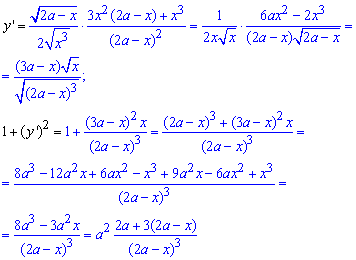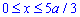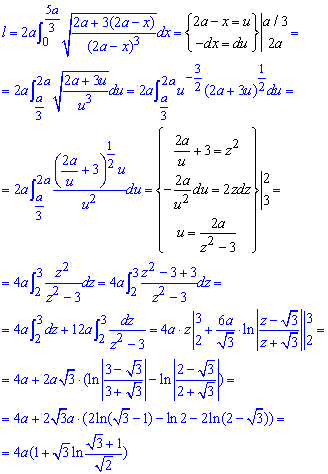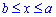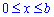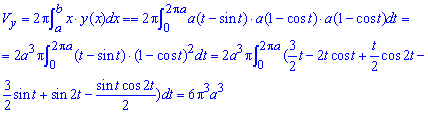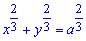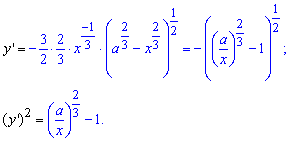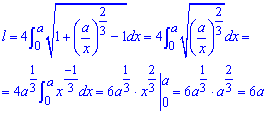{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.
-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
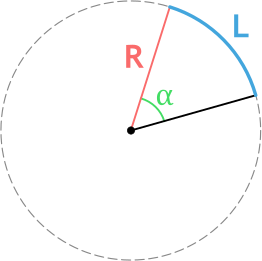
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
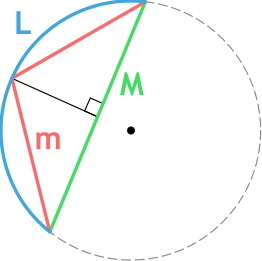
Формула длины дуги окружности по формуле Гюйгенса
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича).
Для запоминания основных моментов схема интегрирования и вычисление дуги кривой из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы графиками кривых.
Найти длины дуг кривых в прямоугольной системе координат
Пример 2.117 (2431) Вычислить длину дуги кривой y=x3/2 (полукубическая парабола Нейля) xє[0;4] .
Вычисление: Найдем производную заданной функции по переменной x:
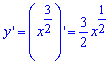
График полукубической параболы Нейля имеет вид
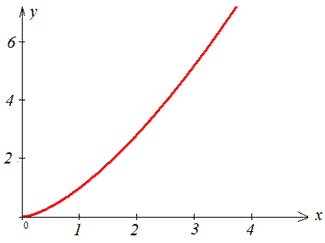
Выписываем пределы интегрирования:
a=0, b=4 (известны из начального условия).
По формуле находим длину дуги на заданном отрезке:
Во время интегрирования для приведения подынтегральной функции к табличному виду выполнили замену переменных.
При этом нужно перечислять пределы интегрирования.
В результате пришлось интегрировать корневую функцию, а длина дуги после вычислений приблизительно равна l=9,07.
Помните, что все длины измеряются в единицах (од.) !!!
Пример 2.118 (2432) Найти длину дуги кривой y2=2px (парабола) xє[0;x0].
Вычисление: Поскольку отрезок дуги параболы задан в пределах [0;x0], то заданная функция будет иметь вид положительной ветки корневой функции 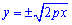
Вычислим производную функции по переменной x:
Запишем пределы интегрирования:
a=0, b=x0 .
График параболы приведен ниже
Вычислим длину дуги через определенный интеграл:
для сведения к простым формулам интегрирования применяем замену переменных, при этом не забываем перечислить изменение пределов интегрирования:
В конце вычислений применено интегрирование частями.
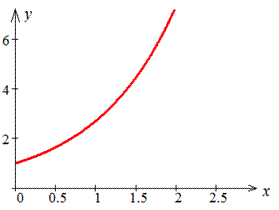
Пример 2.119 (2434) Найти длину дуги кривой y=ex, [0;x0].
Вычисление: Для интегрирования находим производную (по переменной x) экспоненты :
y’=(ex)’=ex.
Поскольку показатель не содержит никаких коэффициентов при переменной, то производная равна самой экспоненте.
Из начального условия выписываем пределы интегрирования:
a=0, b=x0.
График экспоненты имеет вид
Чтобы вычислить длину дуги экспоненты переходим к новой переменной.
Это ведет к изменению и пределов интегрирования и самого дифференциала:
Напоследок расчетов приходим к формуле дуги, которая содержит корневую и логарифмическую зависимости от бегущей координаты.
Пример 2.120 ( 2435) Найти длину дуги кривой x=1/4y2-ln(y)/2, yє[1;e].
Вычисление: Вычислим производную (по переменной y ) заданной функции:
Приведенная формула работает и для обратных функций x=x(y), особенно если функция изменяется как показано на графике
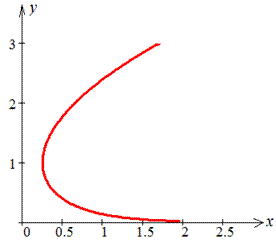
Пределы интегрирования: a=1, b=e .
Находим длину дуги кривой на заданном отрезке:
При возведении к квадрату производной получим простую для интегрирования функцию, которая в результате дает l=(e2+1)/4.
Пример 2.121 (2436) Вычислить длину дуги кривой
Вычисление: Найдем производную по переменной x функции:
Пределы интегрирования для этой дуги равны [0;b].
График исследуемого логарифма имеет вид
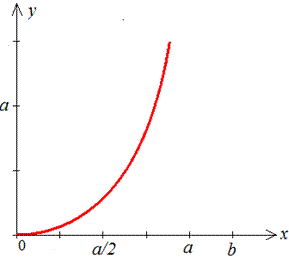
Интегрированием находим длину дуги кривой:
Со всеми превращениями подинтегральной функции попробуйте разобраться самостоятельно.
Пример 2.122 (2437) Вычислить длину дуги кривой y=ln(cos(x)), 0<x<a<Pi/2.
Вычисление: Найдем производную (по переменной x) заданной функции :
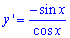
Запишем пределы интегрирования: 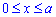
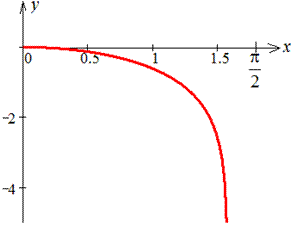
Вычислим длину дуги кривой на заданном отрезке:
Если воспользоваться тригонометрическими формулами то перейдем к тангенсу, а сама длина дуги равна
l=ln(tg (Pi/4+a/2)).
Пример 2.123 Найти длину дуги кривой y=ln(x), 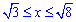
Вычисление: Вычисляем производную от логарифма:
y’=1/x.
Пределы интегрирования переписываем из условия: 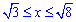
График логарифма имеет вид
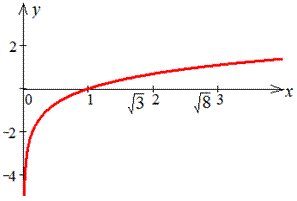
Интегрирование по длине дуги достаточно непростое, требует добрых умений.
Расписав подынтегральную функцию, и применив замену переменных к одному из интегралов, приходим к логарифмам, которые при указанных пределах интегрирования несколько упрощаются.
Невзирая на трехэтажные выражения конечное значение длины дуги выраженно простой зависимостью.
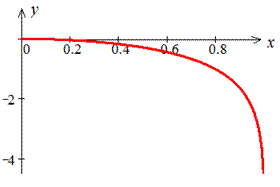
Пример 2.124 Найти длину дуги кривой y=ln(1-x2), x[0;0,5].
Вычисление: Найдем производную (по переменной x) заданной функции :
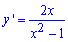
Из начального условия имеем такие пределы интегрирования: [0;0,5].
График исследуемого логарифма имеет вид
Вычисляем длину дуги логарифма:
Если округлить конечное значение, то будем иметь l=0,5986.
Пример 2.125 (2439) Вычислить длину дуги кривой 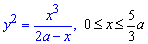
Вычисление: Поскольку график заданной функции симметричен относительно оси Ox, то вычислим длину дуги для положительной части функции
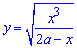
и результат умножим на 2.
Найдем производную функции и саму подинтегральную функцию:
Пределы интегрирования известны:
График веток в декартовой плоскости имеет вид.
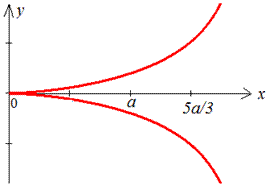
При нахождении длины дуги дважды выполняем замену переменных.
Как и в предыдущих примерах ответ получаем через логарифмы
Кому в учебе придется вычислять подобное задание, просьба разобраться с превращениями.
А еще лучше – придумать и решить подобный пример.
Пример 2.126 (2438) Найти длину дуги кривой 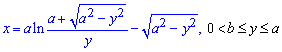
Вычисление: Запишем производную по переменной y трактрисы (см. 2408):
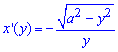
Пределы интегрирования:
График трактрисы имеет вид

По формуле дуги кривой интегрируем и находим длину трактрисы:
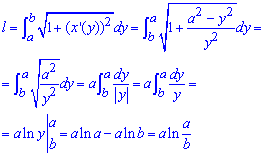
Конечная формула достаточно простая для расчетов.
От края следует несколько отойти, в ином случае длина трактрисы направляется к безконечности.
Пример 2433 Найти длину дуги кривой 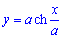
Вычисление: Цепная линия – это кривая, форму которой принимает цепь (нить) под действием силы притяжения, которая подвешена за оба конца.
Поскольку 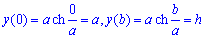
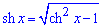
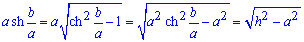
Найдем производную трактрисы:
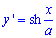
Пределы интегрирования по аргументу следующие:
Рисунок цепной линии приведен ниже
Вычислим длину дуги кривой на заданном отрезке:
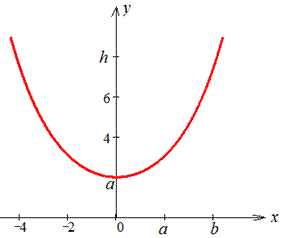
Пример 2440 Найти длину дуги астроиды
Вычисление: Для астроиды оси прямоугольной системы координат делят линию на 4 части (смотри 2429), поэтому длину будем искать для чверти и результат умножим на 4.
Выражаем функцию для чверти астроиды
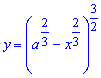
Найдем производную от полученной зависимости и подинтегральную функцию:
Пределы интегрирования: [0;a] (для чверти астроиды).
Вычислить длину дуги астроиды на практике достаточно легко:
Дело в том, что единицы сокращаются и получаем простой табличный интеграл.
В результате длина астроиды равна l=6a.

CHELZabor.ru
ЧелЗабор | Металлоконструкции для дома и дачи
+7 (951) 81-888-77
E-mail: info@chelzabor.ru
Главная
»
Расчеты
»
Расчет дуги
Рассчитать длину дуги, радиус
Порой нужно быстро рассчитать длину дуги, радиус фермы для навеса, для этого на скорую руку был сделан этот простенький калькулятор.
Если известны высота дуги и длина хорды, то это не составит большого труда.
Длина хорды в мм (A)
Высота дуги в мм (B)
Рассчитать
Arc length is defined as the distance between the two points placed on the circumference of the circle and measured along the circumference. Arc length is the curved distance along the circumference of the circle. Length of the arc between two points is always greater than the chord between those two points.
What is Arc Length?
The arc length is defined as the circular distance between two points along the circumference of the circle. The length of the arc is directly dependent on the radius and central angle of the circle. The central angle is the angle subtended by the endpoints of the arc to the center of the circle. It is denoted by θ. It is measured both in degrees and radians. The figure given below shows the arc AB when the radius is r and the central angle is θ.
Arc Length Formula
Length of the arc is calculated using different formulas, the formula used is based on the central angle of the arc. Central angle is measured in degrees or radians, and accordingly, the length of an arc of the circle is calculated. For a circle, the formula for arc length formula is θ times the radius of the circle.
| Arc Length Formula (θ in degrees) | s = 2×π×r ×(θ/360°) |
| Arc Length Formula (θ in radians) | s = θ × r |
| Arc Length Formula (Integral Form) | s = ∫√(1 + (dy/dx)2dx |
There are different cases that are used accordingly to find the required Arc Length
Case 1: When Radius and Angle are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)… (1)
where
r is the radius of the circle
θ is the angle in degrees
L is the Arc lengthArc length when the angle is represented in radians
1 radian = π/180°
Substituting the value of radian in equation (1)
L = 2πr × (θ × / 360)
L = r θ…(2)
where,
r is the radius of the circle
θ is the angle in radians.
Case 2: When Area and Central Angle of the Arc are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)
where,
r is the radius of the circle
θ is the angle in degreesWe need to find the radius of the circle from the given area. After finding the radius, we will substitute the value of radius in the formula.
Area of the circle = πr2
Example: If area of the circle is 314 m2 and centeral angle of the arc is π radian find the length of the arc.
Sloution:
πr2 = 314 m2
r2 = 314/π (π = 3.14)
r2 = 314/3.14
r2 = 100
r = √100 = 10 m
Length of the arc with angle π radians will be:
L = r θ
L = 10 × π
L = 10 × 3.1415
L = 31.415 m
The value of r can be used in the same formula, as discussed above.
Case 3: Arc length In Integral Form
Arc length in integral form is given by:
L = ∫√(1 + (dy/dx)2)dx
where,
Y is the f(x) function
limit of integral is [a, b]
How to Find Arc Length?
Use the steps given below to find the Arc length of the given arc.
Step 1: Mark the central angle and length of the radius of the given arc.
Step 2: Use the formula as given above according to the value of the angle in degrees or radians accordingly.
Step 3: Simplify the above equation to get the required answer.
Also, Check
- Equation of a Circle
- Degrees To Radians
- Radians to Degrees
Solved Examples on Arc Length
Example 1: Find the length of the arc with a radius of 2m and angle π/2 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 2m and θ = π/2 radians
Length of arc = 2 × π/2
Length of arc = π
(π = 3.1415)
Length of arc = 3.1415 m
Thus, the length of the arc is 3.1415 m.
Example 2: Find the length of the arc of function f(x) = 8 between x =2 and x = 4.
Solution:
The formula to calculate the arc length for the function is given by:
L = ∫√(1 + (dy/dx)2)dx
The limit of integral is [a, b]
Substituting the values a = 2, b = 4, and y = 6 or dy/dx = 0 in the above formula,
L = ∫√(1 + (0)2)dx
L = ∫√1 dx
L = ∫1 dx
L = x
(Integral of 1 is x)
The limit of integral is [2, 4]
L = (4 – 2)
L = 2
Thus, the length of the arc of function f(x) = 8 between x = 2 and x = 4 is 2.
Example 3: Find the length of the arc with a radius of 5cm and an angle of 60°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 5cm and θ = 60°
Length of arc = 2πr × (60 / 360)
Length of arc = 2πr × 1/6
Length of arc = 2 × 3.1415 × 5/6
(π = 3.1415)
Length of arc = 5.235cm
Thus, the length of the arc is 5.235cm
Example 4: Find the length of the arc with a radius of 0.5m and an angle of π/4 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 0.5m and θ = π/4 radians
Length of arc = 0.5 × π/4
Length of arc = 0.392 m
(π = 3.1415)
Thus, the length of the arc is 0.392 m
Example 5: Find the length of the arc with a radius of 10cm and an angle of 135°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 10cm and θ = 135°
Length of arc = 2πr × (135/360)
Length of arc = (2 × 3.1415 × 10 × 135)/360°
(π = 3.1415)
Length of arc = 23.56cm
Thus, the length of the arc is 23.56cm.
Example 6: Find the length of the arc with a radius of 20mm and angle π/6 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 20mm and θ = π/6 radians
Length of arc = 20 × π/6
Length of arc = 10.47 mm
(π = 3.1415)
Thus, the length of the arc is 10.47 mm
Example 7: Find the length of the arc with a radius of 2 cm and an angle of 90°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 2cm and θ = 90°
Length of arc = 2πr × (90 / 360)
Length of arc = 2πr × 1/4
Length of arc = 2 ×3.1415 × 2 × 1/4
(π = 3.1415)
Length of arc = 3.1415 cm
Thus, the length of the arc is 3.1415 cm.
FAQs on Arc Length
Question 1: What is the Arc Length of a Circle?
Answer:
Arc length of a circle is the length made by the arc which is measured along its circimference.
Question 2: Length of the arc is measured in which unit?
Answer:
Length of arc is of a circle is either measured in m or in cm.
Question 3: Does arc length is measured in radians?
Answer:
Angles are measured in radians and arc length is a measurement of distance, thus it cannot be measured in radians.
Question 4: How do you find the circumference if the arc length (l) and central angle (θ) are given?
Answer:
When arc length (l) and central angle (θ) is given then the circumference by the formula
Arc Length (L) / Circumference = θ/360º
Last Updated :
20 Jan, 2023
Like Article
Save Article
Как рассчитать длину дуги окружности
На данной странице калькулятор поможет рассчитать длину дуги окружности онлайн. Для расчета задайте радиус, угол между радиусами.
Чтобы найти длину дуги, когда не известен радиус, например, на чертеже или у предмета, то используют формулу Гюйгенса. При расчете по этой формуле есть погрешность, примерно от 0,5% до 0,02%.
Дуга окружности – это часть окружности ограниченная двумя точками.
Через радиус и угол
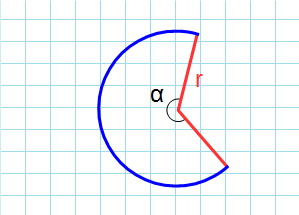
Формула для нахождения площади сектора круга:
π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.
По формуле Гюйгенса
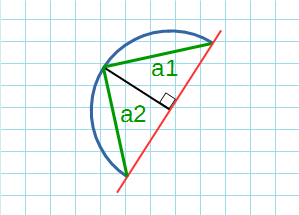
Формула Гюйгенса для нахождения длины дуги окружности:
a1, a2 – хорды.