В прошлых уроках Вы узнали, что такое натуральные числа – это числа, используемые при счете предметов.
Также мы успели поговорить про шкалы – линии с отмеченными на них величинами, которые помогают нам определить ту или иную величину.
Эта информация доступна зарегистрированным пользователям
Сегодня мы рассмотрим в некотором смысле “шкалу” для натуральных чисел – координатный луч, узнаем, что скрывается за этим определением.
Ответим на вопрос, почему луч подходит больше всего для обозначения натуральных чисел, а также научимся определять с помощью него длины отрезков.
Луч- это часть прямой ограниченная с одной стороны точкой, называемой началом луча.
Начертим луч с началом в точке О так, чтобы он шел слева направо, и отметим на нем точку А не очень далеко от начала.
Эта информация доступна зарегистрированным пользователям
Отрезок ОА назовем единичным отрезком.
Далее отложим от точки А следующий отрезок АВ, равный отрезку ОА.
Затем отложим от точки В отрезок ВС, также равный единичному отрезку.
Продолжим процесс, уже не называя точки.
Эта информация доступна зарегистрированным пользователям
Теперь напишем над точкой O число 0, над точкой А число 1, над точкой В число 2, над С – 3 и так далее.
Эта информация доступна зарегистрированным пользователям
Так мы получили шкалу, которую называют координатным лучом.
В самом деле, для шкалы нам необходимы были такие объекты, как штрих, деление, цена деления, посмотрим, чем они представлены в данном случае.
В роли штрихов выступают точки.
Изображая координатный луч, можно точки обозначать как небольшие штрихи, это ничуть не делает рисунок менее точным.
Делением в данном случае является отрезок между любыми соседними точками.
Этот отрезок всегда равен единичному по построению, ведь мы всегда откладывали отрезок, равный единичному.
Ценой деления в данном случае является единица.
Может быть немного непривычно, что единица идет без наименования, ведь на других шкалах обычно цена деления 1 кг, 1 см, 1 км/ч.
Но здесь идет измерение натуральных чисел, поэтому просто единица.
Так что координатный луч вполне можно считать шкалой.
Если же говорить про более конкретное определение, то вот оно.
Координатный луч – луч с указанным для него единичным отрезком.
Нередко к этому определению добавляют помимо единичного отрезка еще два объекта: точку начала отсчета и направление увеличения чисел.
В сущности они не обязательны, ведь на луче уже есть точка – точка начала луча.
А на координатном луче точка начала отсчета и точка начала луча всегда совпадают.
Направление задавать тоже нет необходимости, ведь у луча только одно вполне определенное направление: от начала.
Единичный отрезок же необходим, ведь без него не будет одинакового расстояния между соседними точками и смысла в луче не будет.
Отметим важный момент: в одном координатном луче всегда один единичный отрезок.
Эта информация доступна зарегистрированным пользователям
Мы уже поговорили про координатный луч, но важно понять, почему он “координатный” и как определены координаты в данном случае.
Обычно можно услышать слово “координаты” в географическом контексте.
Когда мы узнаем координаты, а это два числа, то можем однозначно сказать, про какую точку на карте идет речь.
Другими словами, в географическом смысле, координаты являются числами, определяющими положение точки на карте.
В случае с координатным лучом все даже проще.
Ведь если карта – двумерный объект, то есть, если перед нами лежит карта, нам нужно одно число, чтобы определить, как высоко расположена точка, а второе число, чтобы определить насколько она смещена вправо или влево, то на луче точка может быть лишь дальше или ближе от его начала.
Координата точки на координатном луче соответствует количеству единичных отрезков между этой точкой и точкой начала отсчета.
Посмотрим еще раз на рисунок из прошлой главы:
Эта информация доступна зарегистрированным пользователям
Точка А находится на расстоянии одного единичного отрезка от точки начала отсчета.
Точке А соответствует число 1
Точка В находится на расстоянии двух единичных отрезков от точки начала отсчета.
И точке В соответствует число 2
Аналогично каждой следующей точке соответствует число на единицу больше.
Число, соответствующее точке на координатном луче, называют координатой этой точки.
Заметим теперь, как соответствуют друг другу натуральный ряд и координатный луч.
За исключением точки начала отсчета, каждой точке соответствует натуральное число.
Если смотреть от начала отсчета, то координата следующей точки после данной равна следующему натуральному числу после координаты данной точки.
На том же самом рисунке мы видим, что следующее число за координатой точка В (2) , за точкой В идет точка С и координата точки С (3)
Допустим мы знаем, что точки P и Q – соседние, причем Q находится дальше от точки начала отсчета, чем P.
И также мы знаем, что координата точки P равняется 276
Тогда мы сможем сказать координату точки Q, это будет следующее натуральное число после числа 276, то есть ответ: 277
Аналогичная логика работает и в другую сторону.
Координата точки, идущей перед данной, является предыдущим натуральным числом по отношению к координате данной точки.
Эта информация доступна зарегистрированным пользователям
Так, если координата точки В – это 2, то координата точки А будет числом, на единицу меньшим, чем 2, то есть единицей.
Допустим, точки E и R соседние.
Также известно, что R находится дальше от точки начала отсчета, чем Е; а также известна координата точки R, она равна 315
Чтобы найти координату точки Е достаточно взять предыдущее натуральное число от числа 315, это будет число 314
Эти примеры показывают, как натуральный ряд ложится на координатный луч.
Отметим, что именно луч идеально соответствует натуральным числам, ведь и луч, и натуральный ряд ограничены с одной стороны (с начала), но продолжаются бесконечно.
Если же нам надо найти координату точки безотносительно соседних точек, то достаточно отсчитать количество единичных отрезков между данной точкой и точкой начала отсчета.
Эта информация доступна зарегистрированным пользователям
Найдем координату точки Н.
Между ей и точкой О (началом отсчета) 4 единичных отрезка, значит, координата точки Н равна 4
Эта информация доступна зарегистрированным пользователям
Только что в тесте было задание, в котором было необходимо найти разность координат двух точек.
Возможно, вы заметили некоторую закономерность, но если нет, сейчас разберем.
Эта информация доступна зарегистрированным пользователям
Посмотрим на разность координат точек D и C
Мы можем посчитать их координаты. В данном случае они сразу указаны, надо просто вычесть из большей меньшую.
Получится, что разность координат равна единице.
Также заметим, что между точками C и D один единичный отрезок.
Если рассмотрим разность координат точек D и В, то увидим, что разность координат равна 2, а также то, что между ними 2 единичных отрезка.
Правило: чтобы посчитать разность координат двух точек на координатном луче, достаточно посчитать, сколько между ними единичных отрезков.
Данное правило удобно, когда изначально координаты точек неизвестны, но при этом легко посчитать, сколько между ними единичных отрезков.
Теперь поговорим про измерение отрезков.
Допустим, требуется найти длину отрезка AD
Мы можем просто сосчитать количество единичных отрезков между точками А и D
Получится 3 отрезка, следовательно, длина равна 3.
Но можно сделать проще.
Правило: чтобы найти длину отрезка на координатном луче необходимо из координаты точки, дальней от точки начала отсчета, надо вычесть координаты ближней точки.
В случае с отрезком AD необходимо вычесть из координаты точки D (4) координату точки А (1)
Таким образом, длина отрезка AD равна ((mathbf{4-1=3}))
Эта информация доступна зарегистрированным пользователям
Интересно, что с математикой можно столкнуться не только в учебниках, но и в художественной литературе и даже в кинематографе.
Привычно видеть в роли главного героя в фильме какого-либо сильного человека, спортсмена, политика.
Но иногда главным харизматичным героем может быть математик, ученый.
Расскажу про одну достаточно интересную картину, повествующую о нестандартно мыслящемем математике.
А именно про “Человека, который изменил все”.
Эта информация доступна зарегистрированным пользователям
Данный фильм рассказывает про то, как менеджер одного из беднейших в американской лиге бейсбольных клубов “Окленд Атлетикс” нанимает к себе, казалось бы, далекого от спорта человека, похожего на типичного “ботаника”.
Этот человек оказывается выпускником экономического факультета, который решает отбирать игроков в клуб используя методы статистического анализа.
И здесь очень интересна концепция: нередко тот или иной клуб тратит большие деньги, чтобы нанять к себе успешного игрока.
Правда, после того как деньги потрачены, за новый клуб игрок может выступать уже не так хорошо.
Суть статистики заключалась в том, чтобы посмотреть данные множества игроков и начать выявлять таланты, которые еще не успели себя проявить.
Таким образом, клуб нанимает к себе игроков, которые в будущем становятся успешными, да еще и за не очень большие деньги.
Со статистикой можно даже идти дальше и просчитывать не только успехи отдельных игроков, но и всей команды в целом.
Так что данный фильм интересен той концепцией, которую он несет в массы.
Читайте также
Математика
5 класс
Урок № 79
Координатный луч
Перечень рассматриваемых вопросов:
– координатный луч;
– единичный отрезок;
– соотношение единичного отрезка со знаменателем дроби;
– координата точки.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Отрезок – часть прямой, ограниченная с двух сторон точками.
Луч – это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Зададим прямую, на которой указано направление. Отметим на ней точку О. Примем её за начало отсчета.
Отложим на прямой вправо от точки О единичные отрезки.
Единичный отрезок – это расстояние от О до точки, выбранной для измерения.
Обозначим конец первого отрезка числом 1, второго – числом 2 и т. д.
Сформулируем определение.
Прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатной осью или координатным лучом.
С помощью координатной прямой натуральные числа изображаются точками.
Точке О на координатной прямой соответствует число 0. Обозначают: О (0).
Число, которое соответствует данной точке на координатной оси, называют координатой данной точки.
Например, точка А имеет координату 5.
Обозначают А (5).
Таким образом, на координатной прямой можно найти точку, соответствующую натуральному числу. Также с помощью натуральных чисел и числа ноль можно указать положение любой точки на прямой.
А теперь рассмотрим, как отметить на координатном луче дробь.
Чтобы удобно было изображать дробные числа, нужно правильно выбрать длину единичного отрезка.
Удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Например, если требуется изобразить на координатном луче дроби со знаменателем 7, единичный отрезок лучше взять длиной в 7 клеточек. В этом случае изображение дробей на координатном луче будет несложным.
можно изобразить одним единичным отрезком и ещё двумя клеточками.
Если требуется отметить на координатном луче дроби с разными знаменателями, желательно, чтобы число клеточек в единичном отрезке делилось на все знаменатели. Например, для изображения на координатном луче дробей со знаменателями 6, 4 и 12 удобно взять единичный отрезок длиной в двенадцать клеточек. Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берём таких частей столько, каков числитель.
Возьмём единичный отрезок, разделим на шесть частей и возьмём одну из них.
Тренировочные задания
№ 1. Подберите правильные названия к числам. Разместите нужные подписи под изображениями.
Варианты ответов: смешанное число; правильная дробь; неправильная дробь.
Чтобы правильно выполнить задание, необходимо вспомнить, какую дробь называют правильной, а какую неправильной. А также, что называют смешанным числом.
Правильный ответ:
Варианты ответа: 9; 6; 4; 3; 2
Мы знаем, что удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Знаменатель равен 9, значит, единичный отрезок следует выбирать в 9 клеток.
Правильный ответ: 9.
5.1. Координатный луч. Единичный отрезок
Натуральные числа можно изображать на луче. Построим луч с началом в точке О, направив его слева – направо, направление отметим стрелкой.
Началу луча (точке О) поставим в соответствие число 0 (ноль). Отложим от точки О отрезок ОА произвольной длины. Точке А поставим в соответствие число 1 (один). Длину отрезка ОА будем считать равной 1 (единице). Отрезок АВ = 1 называется единичным отрезком. Отложим от точки А в направлении луча отрезок АВ = ОА. Поставим точке В в соответствие число 2. Заметим, что точка В находится от точки О на расстоянии в два раза большем, чем точка А. Значит, длина отрезка ОВ равна 2 (двум единицам). Продолжая откладывать в направлении луча отрезки, равные единичному, будем получать точки, которым соответствуют числа 3, 4, 5, и т.д. Данные точки удалены от точки О соответственно на 3, 4, 5, и т.д. единиц.
Луч, построенный таким способом, называется координатным или числовым. Начало числового луча, точка О, называется точкой отсчета. Числа, поставленные в соответствие точкам на этом луче, называются координатами этих точек (отсюда: координатный луч). Пишут: О(0), А(1), В(2), читают: «точка О с координатой 0 (ноль), точка А с координатой 1 (один), точка В с координатой 2 (два)» и т.д.
Любое натуральное число n можно изобразить на координатном луче, при этом соответствующая ему точка P будет удалена от точки О на n единиц. Пишут: ОP = n и P(n) – точка P (читают: “пэ”) с координатой n (читают: “эн”). Например, чтобы отметить на числовом луче точку К(107), необходимо от точки О отложить 107 отрезков, равных единичному. В качестве единичного можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на числовом луче необходимые натуральные числа. Рассмотрите пример
5.2. Шкала
Важным применением числового луча являются шкалы и диаграммы. Они используются в измерительных приборах и устройствах, при помощи которых измеряют различные величины. Одним из основных элементов измерительных приборов является шкала. Она представляет собой числовой луч, нанесенный на металлическое, деревянное, пластиковое, стеклянное или другое основание. Часто шкала выполнена в виде окружности или части окружности, которые разделены штрихами на равные части (деления-дуги) подобно числовому лучу. Каждому штриху на прямой или круговой шкале поставлено в соответствие определенное число. Это значение измеряемой величины. Например, числу 0 на шкале термометра соответствует температура 00С, читают: «ноль градусов Цельсия». Это температура, при которой начинает таять лед (или начинает замерзать вода).
Используя измерительные приборы и инструменты со шкалами, определяют значение измеряемой величины по положению указателя на шкале. Чаще всего указателем служат стрелки. Они могут перемещаться вдоль шкалы, отмечая значение измеряемой величины (например, стрелка часов, стрелка весов, стрелка спидометра – прибора для измерения скорости, рисунок 3.1.). Подобна смещающейся стрелке граница столбика ртути или подкрашенного спирта в термометре (рисунок 3.1). В некоторых приборах движется не стрелка вдоль шкалы, а шкала перемещается относительно неподвижной стрелки (метки, штриха), например, в напольных весах. В некоторых инструментах (линейка, рулетка) указателем служат границы самого измеряемого предмета.
Промежутки (части шкалы) между соседними штрихами шкалы называются деления. Расстояние между соседними штрихами, выраженное в единицах измеряемой величины, называется ценой деления (разность чисел, которым соответствуют соседние штрихи шкалы.) Например, цена деления спидометра на рисунке 3.1. равна 20 км/ч (двадцать километров в час), а цена деления комнатного термометра на рисунке 3.1. равна 10С (один градус Цельсия).
Диаграмма
Для видимого изображения величин используют линейные, столбчатые или круговые диаграммы. Диаграмма состоит из числового луча-шкалы, направленного слева – направо или снизу – вверх. Кроме того на диаграмме помещены отрезки или прямоугольники (столбцы), изображающие сравниваемые величины. При этом длина отрезков или столбцов в единицах шкалы равна соответствующим величинам. На диаграмме возле числового луча-шкалы подписывают название единиц измерения, в которых отложены величины. На рисунке 3.2. изображена столбчатая диаграмма, а на рисунке 3.3 линейная.
3.2.1. Величины и приборы для их измерения
В таблице приведены названия некоторых величин, а также приборов и инструментов, предназначенных для их измерения. (Жирным шрифтом выделены основные единицы Международной системы единиц).
5.2.2. Термометры. Измерение температуры
На рисунке 3.4 приведены термометры, в которых использованы разные температурные шкалы: Реомюра (°R), Цельсия (°С) и Фаренгейта (°F).В них использован один и тот же температурный интервал – разность температур кипения воды и плавления льда. Этот интервал разделён на различное число частей: в шкале Реомюра – на 80 частей, шкале Цельсия – на 100 частей, в шкале Фаренгейта – на 180 частей. При этом в шкалах Реомюра и Цельсия температуре таяния льда соответствует число 0 (ноль), а в шкале Фаренгейта – число 32. Единицы температуры в этих термометрах: градус по Реомюру, градус по Цельсию, градус по Фаренгейту. В устройстве термометров используется свойство жидкостей (спирта, ртути) расширяться при нагревании. При этом различные жидкости по-разному расширяются при нагревании, что видно на рисунке 3.5, где штрихи для столбика спирта и ртути не совпадают при одинаковой температуре.
5.2.3. Измерение влажности воздуха
Влажность воздуха зависит от количества в нём водяных паров. Например, летом в пустыне воздух сухой, влажность его низкая, так как в нём содержится мало паров воды. В субтропиках, например, в Сочи влажность высокая, в воздухе много водяных паров. Измерить влажность можно с помощью двух термометров. Один из них обычный (сухой термометр). У второго шарик обёрнут влажной тканью (влажный термометр). Известно, что при испарении воды температура тела понижается. (Вспомните озноб при выходе из моря после купания). Поэтому влажный термометр показывает более низкую температуру. Чем суше воздух, тем больше разность показаний двух термометров. Если показания термометров одинаковы (разность равна нулю), то влажность воздуха равна 100 %. В этом случае выпадает роса. Прибор, измеряющий влажность воздуха, называется психрометром (рисунок 3.6). Он снабжён таблицей, в которой приведены: показания сухого термометра, разность показаний двух термометров, влажность воздуха в процентах. Чем ближе влажность к 100%, тем более влажный воздух. Нормальная влажность в помещениях должна быть равна около 60%.
Блок 3.3. Самоподготовка
5.3.1. Заполните таблицу
Отвечая на вопросы таблицы, заполняйте свободную колонку («Ответ»). При этом используйте рисунки приборов в блоке «Дополнительный».
760 мм. рт. ст. считается нормальным. На рисунке 3.11 показано изменение атмосферного давления при подъёме на самую высокую гору Эверест.
Постройте линейную диаграмму изменения давления, отложив на вертикальном луче высоту над уровнем моря, а по горизонтали давление.
Блок 5.4. Проблемный
Построение числового луча с единичным отрезком заданной длины
Для решения этой учебной проблемы работайте по плану, приведенному в левой колонке таблицы, при этом правую колонку рекомендуется закрыть листом бумаги. Ответив на все вопросы, сопоставьте свои выводы с приведёнными решениями.
Блок 5.5. Фасетный тест
Числовой луч, шкала, диаграмма
В задачах фасетного теста использованы рисунки из таблицы. Все задачи начинаются так: «ЕСЛИ числовой луч представлен на рисунке …., то…»
ЕСЛИ: числовой луч представлен на рисунке… Таблица
ТО:
- Количество единиц между соседними штрихами числового луча.
- Координаты точек А, В, С, D.
- Длина (в сантиметрах) отрезков АВ, ВС, АD, ВD соответственно.
- Длина (в метрах) отрезков АВ, ВС, АD, ВD соответственно.
- Натуральные числа, расположенные на числовом луче левее точки D.
- Натуральные числа, расположенные на числовом луче между точками А и С.
- Количество натуральных чисел, лежащих на числовом луче между точками А и D.
- Количество натуральных чисел, лежащих на числовом луче между точками В и С.
- Цена деления шкалы прибора.
- Скорость автомобиля в км/ч, если стрелка спидометра указывает на точки А, В, С, D соответственно.
- Величина (в км/ч), на которую увеличилась скорость автомобиля, если стрелка спидометра переместилась из точки В в точку С.
- Величина скорости автомобиля после того, как водитель уменьшил скорость на 84 км/ч (перед уменьшением скорости стрелка спидометра указывала на точку D).
- Масса груза на весах в центнерах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Масса груза на весах в килограммах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Масса груза на весах в граммах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Количество учеников в 5 классе.
- Разность между количеством учеников, успевающих на «4», и количеством учеников, успевающих на «3».
- Отношение количества учеников, успевающих на «4» и «5», к количеству учеников, успевающих на «3».
РАВНО (равна, равны, это):
а) 10 б) 6,12,3,3 в) 1 г) 99,102,106,104 д) 2 е) 201,202 ж) 49 з) 3500,3000,8000,4500
и) 5,2,1,4 к) 599 л) 6,3,3,9 м) 10,4,16,7 н) 100 о) 4 км/ч п) 65,85,105,115 р) 7,2,4,6 с) 20,20,50,30 т) 0 у) 700,600,1600,900 ф) 1,2,3,4,5,6 х) 25,10,5,20 ц) 3,4,5,2 ч) 203,197,200,206 ш) 15,20,25,10 щ) 1599 ы) 11,12,13,14,15 э) 30,60,15,15 ю) 0,700,1300,1600 я) 100,100,250,150 аа) 30,15,15,45 бб) 4 вв) 1,2,3,4,5 гг) 17 дд) 500 кг ее) 19 жж) 80 зз) 100,101,102,103,104,105 ии)5,6 кк) 28,64,100,164 лл) 1500000,3000000,4500000 мм) 11 нн) 36 оо) 1500,3000,4500 пп) 7 рр) 24 сс) 15,30,45
Блок 5.6. Учебная мозаика
В заданиях мозаики использованы приборы из блока «Дополнительный». Ниже приведено поле мозаики. На нём указаны названия приборов. Кроме того для каждого прибора обозначены: измеряемая величина (В), единица измерения величины (Е), показание прибора (П), цена деления шкалы (Ц). Далее помещены ячейки мозаики. Прочитав ячейку, вы должны сначала определить прибор, к которому она относится, и поставить в окружность ячейки номер прибора. Затем надо догадаться, о чём эта ячейка. Если речь идёт об измеряемой величине, надо к номеру приписать букву В. Если это единица измерения – поставить букву Е, если показание прибора – букву П, если цена деления – букву Ц. Таким образом надо обозначить все ячейки мозаики. Если ячейки вырезать и расположить так, как на поле, то можно систематизировать сведения о приборе. В компьютерном варианте мозаики при правильном расположении ячеек создаётся рисунок.
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Запомните!
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой.
Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: «(·) A» — точка «А».
Прямая
Запомните!
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
- Через две точки можно провести единственную прямую.
- Две прямые могут пересекаться только в одной точке.
- Через одну точку можно провести бесконечное множество прямых.
Способы обозначения прямых
- Строчной латинской буквой:
Прямая «a».
- Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены
точки, расположенные на прямой.
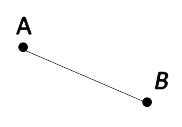
Прямая «АB».
Луч
Запомните!
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки.
У луча есть начало, но нет конца.
Способы обозначения лучей
- Строчной латинской буквой:
Луч «c».
- Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а
вторая точка лежит на луче.
Луч «AB».
Отрезок
Запомните!
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка).
У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Отрезок «AB».
Ломаная
Запомните!
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими
буквами.
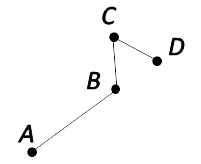
Ломаная «ABCD».
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Запомните!
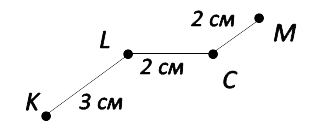
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из
которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную
геометрическую фигуру — угол.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 февраля 2017 в 9:40
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
6. (4 балла) Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
25 февраля 2017 в 9:37
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Ильназ Хуснутдинов
Профиль
Благодарили: 0
Сообщений: 2
Дан отрезок MP длиной 39 см. На нем отмечены точки G и H таким образом, что длины отрезков GP = 26 см, MH = 23 см. Найти длину отрезка GH в дециметрах.
0
Спасибо
Ответить
13 сентября 2016 в 8:06
Serega Pavlichenko
Профиль
Благодарили: 0
Сообщений: 1
Serega Pavlichenko
Профиль
Благодарили: 0
Сообщений: 1
найдите длину единичного отрезка координатного луча.Отметьте на координатном луче точки Е(2) и Д(5)
0
Спасибо
Ответить
19 сентября 2016 в 14:44
Ответ для Serega Pavlichenko
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Единичный отрезок- это отрезок равный 1делению. Точка E — на расстоянии 2 деления от начала луча, а точка Д — на расстоянии 5 делений от начала луча.
0
Спасибо
Ответить
10 июня 2016 в 9:50
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Объясните, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой.
0
Спасибо
Ответить
24 июня 2016 в 12:39
Ответ для Дарья Бондарь
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
отрезок, образующий с данной прямой угол 90 градусов
0
Спасибо
Ответить
9 июня 2016 в 10:28
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Дарья Бондарь
Профиль
Благодарили: 0
Сообщений: 4
Какими инструментами пользуются для измерения расстояний?
0
Спасибо
Ответить
9 июня 2016 в 10:53
Ответ для Дарья Бондарь
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Линейка, рулетка. Расстояние можно измерить по карте, зная масштаб и имея линейку.
0
Спасибо
Ответить
19 марта 2016 в 17:01
Настюшка Петрухова
Профиль
Благодарили: 0
Сообщений: 1
Настюшка Петрухова
Профиль
Благодарили: 0
Сообщений: 1
Дается отрезок, единичный отрезок равен 10 клеточкам. Как на нем указать 0,75 и 2,15???
0
Спасибо
Ответить
25 марта 2016 в 19:21
Ответ для Настюшка Петрухова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если я правильно понимаю задание, то необходимо нарисовать соответствующие отрезки. Если единичный отрезок равен 10 клеточек, то 0,75 от него =10*0,75=7,5 клеток. А 2,15 = 2,15*10=21,5 клетка.
0
Спасибо
Ответить
3 октября 2015 в 11:37
Ольга Сырая
Профиль
Благодарили: 0
Сообщений: 1
Ольга Сырая
Профиль
Благодарили: 0
Сообщений: 1
На прямой поставили 3 точки. Сколько получилось отрезков? Мы решили, что 2. Но это олимпиадная задача и ответ пришел -3. Неужели АС это тоже отрезок?
0
Спасибо
Ответить
6 октября 2015 в 17:56
Ответ для Ольга Сырая
Альбина Серб
Профиль
Благодарили: 0
Сообщений: 2
Альбина Серб
Профиль
Благодарили: 0
Сообщений: 2
да
0
Спасибо
Ответить
25 сентября 2015 в 19:16
Снежана Бабюк
Профиль
Благодарили: 0
Сообщений: 1
Снежана Бабюк
Профиль
Благодарили: 0
Сообщений: 1
выберите геометрические фигуры понятие которых не определяется:
прямая, квадрат, плоскость, треугольник, окружность, точка, полупрямая, отрезок.
0
Спасибо
Ответить
12 сентября 2016 в 11:39
Ответ для Снежана Бабюк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Прямая, плоскость и точка.
0
Спасибо
Ответить
15 сентября 2015 в 13:19
Марьям Туманова
Профиль
Благодарили: 0
Сообщений: 1
Марьям Туманова
Профиль
Благодарили: 0
Сообщений: 1
начерти отрезок мн длиной 4 см.начерти отрезок, каторий длиннееотрезкамн: а)на 3см; б)в3раза.какой длиныполулся каждый отрезок?
0
Спасибо
Ответить
17 сентября 2015 в 21:23
Ответ для Марьям Туманова
Ега Превосходный
Профиль
Благодарили: 0
Сообщений: 2
Ега Превосходный
Профиль
Благодарили: 0
Сообщений: 2
1 отрезок 4 см., второй 7 см., третий в трираза больше когого? если первого то полусится12см если вророго то получится 21см записать так( 4+3)* 3=21 см
0
Спасибо
Ответить
Содержание:
- § 1 Координатный луч
- § 2 Определение координат точки
§ 1 Координатный луч
В этом уроке Вы научитесь строить координатный луч, а также определять координаты точек, расположенных на нем.
Чтобы построить координатный луч, нам сначала потребуется, конечно же, сам луч.
Обозначим его OX, точка O – начало луча.
Забегая вперед, скажем, что точку O называют началом отсчета координатного луча.
Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.
Итак, начертим луч ОХ горизонтально слева направо и обозначим его направление стрелкой. Отметим на луче точку Е.
Над началом луча (точкой О) напишем 0, над точкой Е – цифру 1.
Отрезок ОЕ называют единичным.
Далее на луче отложим отрезок ЕА, равный единичному отрезку, и над точкой А напишем цифру 2.
Так, шаг за шагом, откладывая единичные отрезки, получим бесконечную шкалу.
Числа 0, 1, 2 называют координатами точек О, Е и А. Пишут точка О и в скобках указывают ее координату ноль – О(о), точка Е и в скобках ее координата один – Е(1), точка А и в скобках ее координата два – А(2).
Таким образом, для построения координатного луча необходимо:
1. начертить луч ОХ горизонтально слева направо и обозначить его направление стрелкой, над точкой O написать число 0;
2. нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1;
3. на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному и тоже поставить штрих, далее от конца уже этого отрезка нужно отложить еще один единичный отрезок, также отметить штрихом и так далее;
4. чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2, 3, 4, и так далее.
§ 2 Определение координат точки
Давайте выполним задание:
На координатном луче нужно отметить следующие точки: точку М с координатой 1, точку Р с координатой 3 и точку А с координатой 7.
Построим координатный луч с началом в точке О. Единичный отрезок этого луча выберем 1 см, то есть 2 клетки (через 2 клетки от нуля поставим штрих и число 1, дальше еще через две клетки – штрих и число 2; затем 3; 4; 5; 6; 7 и так далее).
Точка М будет расположена правее нуля на две клетки, точка Р будет расположена правее нуля на 6 клеток, так как 3 умножить на 2, будет 6, и точка А – правее нуля на 14 клеток, так как 7 умножить на 2, получится 14.
Следующее задание:
Найдите и запишите координаты точек А; В; и С отмеченных на данном координатном луче
Решение:
Данный координатный луч имеет единичный отрезок, равный одной клетке, значит координата точки А равна 4, координата точки В равна 8, координата точки С равна 12.
Подведем итог, луч ОХ с началом отсчета в точке О, на котором указаны единичный отрезок и направление, называют координатным лучом. Координатный луч представляет собой не что иное, как бесконечную шкалу.
Число, которое соответствует точке координатного луча, называется координатой этой точки.
Например: А и в скобках 3.
Читают: точка А с координатой 3.
Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа 0 и 1. В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.
Таким образом, в этом уроке Вы научились строить координатный луч, а также определять координаты точек, расположенных на координатном луче.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.