Единичный вектор
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
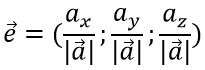
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Единичные векторы: характеристики, как получить, примеры
Содержание:
В единичные векторы – это те, модуль, величина или размер которых равны числовому значению. Единичные векторы полезны для указания направления других неединичных векторов.
Помните, что векторы – это математические объекты, которые математически представляют физические величины, зависящие от направления, такие как сила, скорость, ускорение и другие.
Независимо от физической величины, с которой они связаны, единичные векторы лишены единиц измерения, и их размер всегда равен 1, чистому числу.
Например, скорость частицы, движущейся со скоростью 3 м / с в положительном направлении декартовой оси X, обозначается: v = (3 м / с) я, где жирным шрифтом обозначены векторные величины. В этом примере модуль v составляет 3 м / с, а модуль единичного вектора я равно 1 (без единиц).
Модуль, направление и смысл
Учитывая, насколько важно установить ориентацию этих величин для того, чтобы узнать их влияние, векторы имеют три важные характеристики: величину или модуль, связанный с размером вектора, направление и смысл. При представлении векторной величины необходимо четко указать эти аспекты.
Теперь единичный вектор может иметь любое направление и любое значение, но величина всегда должна быть равна 1.
Единичные векторы используются для обозначения конкретного направления в пространстве или на плоскости. Если, например, нам нужно работать со всеми силами, которые действуют вдоль горизонтальной оси, то единичный вектор в этом направлении помогает нам отличать эти силы от других, направленных в другом направлении.
А чтобы отличить их от неединичных векторов, в печатных буквах обычно используется жирный шрифт, а сверху ставится каретка, например:
Характеристики единичного вектора
Математически единичный вектор:
Итак, мы можем установить, что:
-Модуль единичного вектора всегда равен 1, не имеет значения, является ли это силой, скоростью или другим вектором.
-Унитарные векторы имеют определенное направление, а также смысл, например единичный вектор в вертикальном направлении, который может иметь смысл вверх или вниз.
-Единичные векторы имеют точку происхождения. Когда она представлена декартовой системой координат, эта точка совпадает с началом системы: (0,0), если это плоскость, или (0,0,0), если вектор находится в трехмерном пространстве.
-Также с единичными векторами вы можете выполнять все операции сложения, вычитания и умножения векторов, которые выполняются с использованием обычных векторов. Следовательно, можно умножать единичный вектор на скаляр, а также выполнять точечное произведение и кросс-произведение.
-С помощью единичного вектора в определенном направлении могут быть выражены другие векторы, которые также ориентированы в этом направлении.
Единичные векторы в пространстве
Чтобы выразить любой вектор в пространстве или на плоскости, можно использовать набор единичных векторов, перпендикулярных друг другу, которые образуют ортонормированный базис. Каждое из трех предпочтительных направлений пространства имеет собственный единичный вектор.
Вернемся к примеру сил, направленных по горизонтальной оси. Это ось абсцисс, которая имеет две возможности: вправо и влево. Предположим, у нас есть единичный вектор на оси x, направленный вправо, который мы можем обозначить любым из следующих способов:
Любой из них действителен. Теперь предположим, что сила F1 величиной 5 Н вдоль этой оси и направленной вправо такую силу можно выразить как:
Если бы сила была направлена вдоль оси x, но в противоположном направлении, то есть влево, то для установления этой разницы можно было бы использовать отрицательный знак.
Например, сила величиной 8 Н, расположенная по оси x и направленная влево, будет выглядеть так:
А для векторов, которые не направлены вдоль декартовых осей, также есть способ представить их в терминах ортогональных единичных векторов, используя их декартовы компоненты.
Как получить / рассчитать единичный вектор?
Чтобы вычислить единичный вектор в направлении любого произвольного вектора v, применяется следующая формула:
Это модуль или величина вектора v, квадрат которого рассчитывается так:
Произвольный вектор через единичный вектор
В качестве альтернативы вектор v можно выразить так:
То есть произведение его модуля и соответствующего единичного вектора. Именно это и было сделано ранее, когда говорилось о силе величиной 5 Н, направленной вдоль положительной оси x.
Графическое представление
Графически это видно на этом изображении, где вектор v он синего цвета, а соответствующий единичный вектор в его направлении – красным.
В этом примере вектор v его величина больше, чем у единичного вектора, но объяснение справедливо, даже если это не так. Другими словами, у нас могут быть векторы, которые, например, в 0,25 раза больше единичного вектора.
Примеры единичных векторов
Перпендикулярные единичные векторы i, j и k
Как мы видели ранее, перпендикулярные единичные векторы я, j Y k они очень полезны для представления любого другого вектора на плоскости или в пространстве, а также для выполнения векторных операций. В терминах этих векторов произвольный вектор v представлен как:
v = vИкся + vYj + vzk
Где VИкс, vY и Vz – прямоугольные компоненты вектора v, которые являются скалярами – жирным шрифтом они не выделяются в печатном тексте.
Закон Кулона
Единичные векторы часто появляются в физике. Вот, например, закон Кулона, который количественно описывает взаимодействие двух точечных электрических зарядов.
В нем говорится, что сила F Притяжение или отталкивание между указанными зарядами пропорционально их произведению, обратно пропорционально квадрату расстояния, которое их разделяет, и направлено в направлении единичного вектора, соединяющего заряды.
Этот вектор обычно представлен:
А закон Кулона в векторной форме выглядит так:
Упражнение решено
Найдите единичный вектор в направлении вектора v = 5я + 4j -8kв условных единицах.
Решение
Применяется определение единичного вектора, данное выше:
Но сначала мы должны вычислить модуль вектора, который, поскольку он состоит из трех компонентов, определяется:
|v| 2 = (5) 2 + (4) 2 + (-8) 2 = 25 + 16 + 64 = 105
Поэтому модуль v это:
Искать единичный вектор просто:
Что в конечном итоге приводит нас к следующему:
v = 0.488 я + 0.390 j – 0.781 k
Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Резник, Р. (1999). Физический. Том 1. 3-е изд. На испанском языке. Compañía Editor Continental S.A. de C.V.
История машин: от истоков до наших дней
Каковы жизненно важные функции живых существ?
Векторная алгебра — основные понятия с примерами решения и образцами выполнения
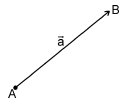
Вектором называется направленный отрезок. Вектор обозначается либо символом  (
(  — точка начала,
— точка начала,  — точка конца вектора), либо
— точка конца вектора), либо  . В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
. В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
2. Длиной (модулем) вектора 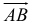 называется длина отрезка
называется длина отрезка 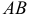 . Модуль вектора обозначается
. Модуль вектора обозначается 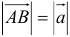 .
.
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 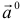 направления вектора
направления вектора  называется ортом вектора
называется ортом вектора  и определяется по формуле
и определяется по формуле 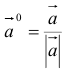 .
.
4. Вектор называется нулевым, если его начало и конец совпадают 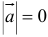 ; любое направление можно считать направлением нулевого вектора.
; любое направление можно считать направлением нулевого вектора.
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 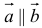 . Необходимым и достаточным условием коллинеарности векторов
. Необходимым и достаточным условием коллинеарности векторов  и
и 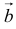 является существование такого числа
является существование такого числа 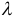 , что
, что 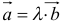 .
.
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 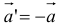 называется противоположным вектору
называется противоположным вектору  , если модули их равны, а направления противоположны.
, если модули их равны, а направления противоположны.
8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
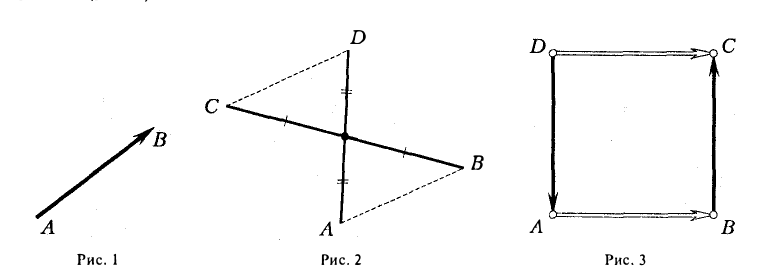
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
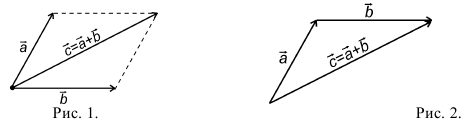
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
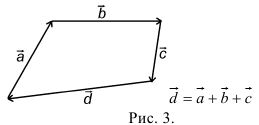
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).

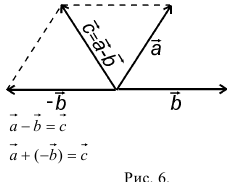
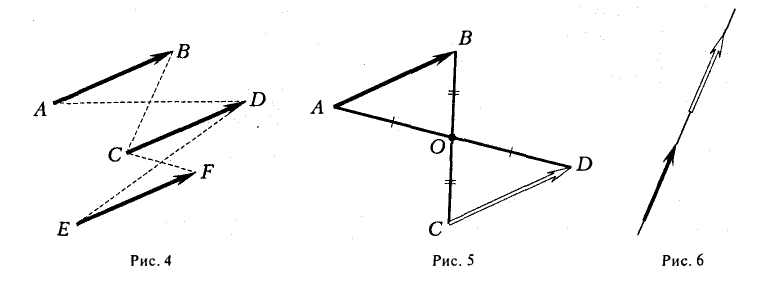
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
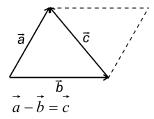
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора  на число
на число  называется вектор
называется вектор 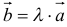 , который имеет :
, который имеет :
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
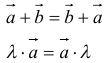
- сочетательный:
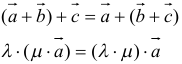
- распределительный:
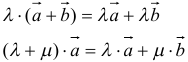

Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки 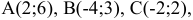
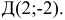
1) Найти координаты векторов
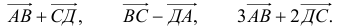
2) Написать разложение этих векторов по базису 
3) Найти длины этих векторов
4) Найти скалярное произведение 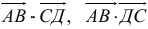
5) Найти угол между векторами  и
и 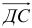 .
.
6) Найти разложение вектора 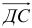 по базису
по базису  и
и 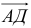
Решение:
1) Вычислим координаты векторов  и
и 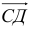 (нужно из координат точки его конца вычесть координаты его начала):
(нужно из координат точки его конца вычесть координаты его начала):
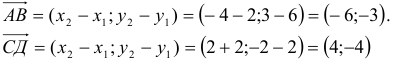
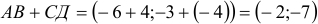 , аналогично,
, аналогично, 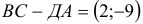
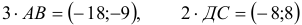 и
и 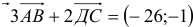
2) 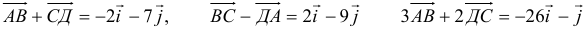
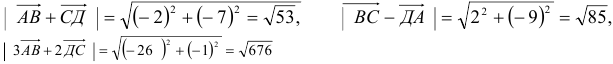
4) Для вычисления угла между векторами воспользуемся формулой:
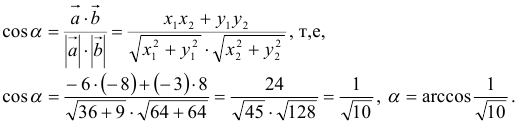
5) Разложить вектор 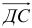 по векторам
по векторам  и
и 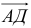 — это значит представить вектор
— это значит представить вектор 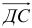 в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и 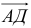 , т. е.
, т. е.
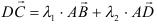 , где
, где 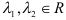 . Имеем
. Имеем 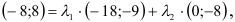
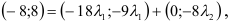
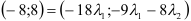 , но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем
, но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем 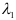 и
и 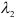 .
.
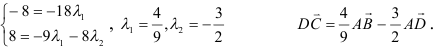
Задача:
а). Даны векторы 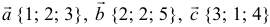 и
и 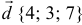 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 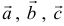 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 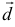 в этом базисе.
в этом базисе.
Решение:
Три вектора образуют базис, если 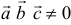 .
.
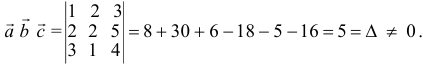
Найдем координаты вектора 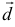 в базисе
в базисе 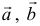 и
и 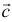 .
.
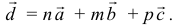
Два вектора равны, если их соответствующие координаты равны.
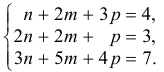
Решим систему методом Крамера:
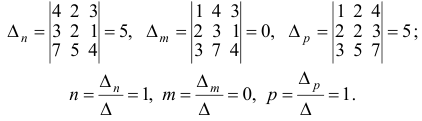
Ответ:  .
.
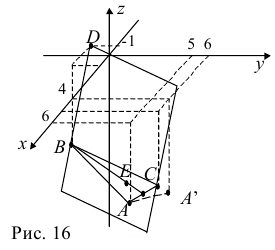
Задача:
Даны координаты вершин тетраэдра 
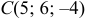 и
и 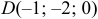 . Найти: 1) координаты точки пересечения медиан треугольника
. Найти: 1) координаты точки пересечения медиан треугольника 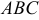 ; 2) уравнение прямой, проходящей через вершину
; 2) уравнение прямой, проходящей через вершину  параллельно медиане, проведенной из вершины
параллельно медиане, проведенной из вершины  треугольника
треугольника  ; 3) координаты точки, симметричной точке
; 3) координаты точки, симметричной точке  относительно плоскости
относительно плоскости  . Сделать чертёж.
. Сделать чертёж.
Решение:
1) Найдем координаты т. 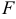 середины отрезка
середины отрезка 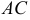 (рис. 16):
(рис. 16): 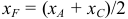
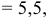
Точка  пересечения медиан треугольника делит медиану
пересечения медиан треугольника делит медиану  в отношении
в отношении 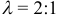 , считая от вершины
, считая от вершины 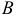 . Найдем координаты точки
. Найдем координаты точки 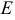 :
:
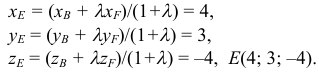
2) Найдем направляющий вектор прямой 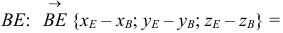
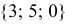 . Уравнение прямой, проходящей через вершину
. Уравнение прямой, проходящей через вершину  параллельно прямой
параллельно прямой  :
:
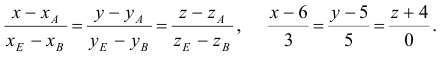
3) Найдем уравнение плоскости  :
:
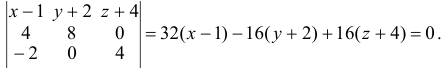
Найдем каноническое уравнение прямой, перпендикулярной плоскости  и проходящей через т.
и проходящей через т.  :
: 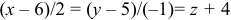 . Запишем каноническое уравнение прямой в параметрическом виде:
. Запишем каноническое уравнение прямой в параметрическом виде: 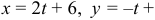
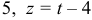 .
.
Найдем координаты точки 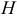 пересечения плоскости
пересечения плоскости  и найденной прямой:
и найденной прямой: 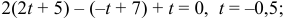
Координаты точки 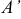 симметричной точке
симметричной точке  относительно плоскости
относительно плоскости  —
— 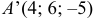 .
.
Ответ: 1) координаты точки пересечения медиан 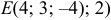 уравнение прямой
уравнение прямой 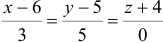 ; 3) координаты симметричном точки
; 3) координаты симметричном точки 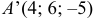 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 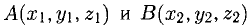 пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается
пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается 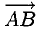 или
или 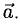 Длина вектора, обозначаемая
Длина вектора, обозначаемая  , АВ или
, АВ или 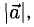 а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала:
а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала: 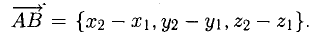 Тогда длина вектора найдется так:
Тогда длина вектора найдется так:
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 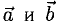 называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут
называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут 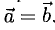 Равные векторы имеют равные координаты.
Равные векторы имеют равные координаты.
Векторы 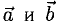 называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления:
называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления: 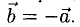
Вектор называется нулевым, если его модуль равен нулю, и обозначается 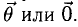
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало  совмещено с концом
совмещено с концом 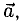 то начало
то начало 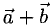 совпадает с началом
совпадает с началом 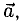 а конец — с концом
а конец — с концом 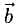 (рис. 3.1).
(рис. 3.1).
2.Если начала векторов 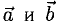 совмещены, то начало
совмещены, то начало  совпадает с концом
совпадает с концом 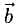 , а конец
, а конец  совпадает с концом
совпадает с концом 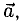 (рис. 3.2).
(рис. 3.2).
3.При умножении вектора  на число (скаляр)
на число (скаляр) 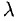 длина вектора умножается на
длина вектора умножается на 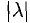 , а направление сохраняется, если
, а направление сохраняется, если 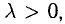 и изменяется на противоположное, если
и изменяется на противоположное, если 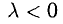 (рис. 3.3).
(рис. 3.3).
Вектор 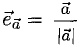 называется ортом, или единичным вектором вектора
называется ортом, или единичным вектором вектора 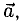 его длина равна единице:
его длина равна единице: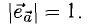
3°. Запись ci — 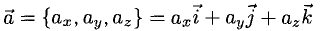 означает, что вектор
означает, что вектор  имеет координаты
имеет координаты 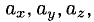 или
или  разложен по базису
разложен по базису 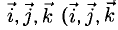 — орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
— орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
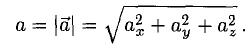
4°. Числа 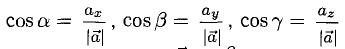 называются направляющими косинусами вектора
называются направляющими косинусами вектора  — углы между вектором
— углы между вектором  и координатными осями Ох, Оу, Oz соответственно. Единичный вектор
и координатными осями Ох, Оу, Oz соответственно. Единичный вектор 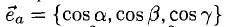 — орт вектора
— орт вектора  . Для любого вектора справедливо:
. Для любого вектора справедливо: 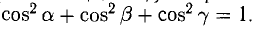
5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 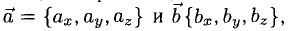 тогда
тогда
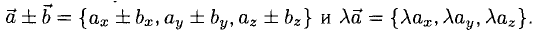
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 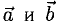 , устанавливаемое равенством
, устанавливаемое равенством 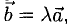 может быть записано соотношениями
может быть записано соотношениями 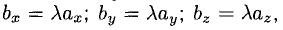 из которых следует пропорциональность их координат:
из которых следует пропорциональность их координат: 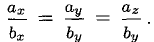
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 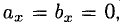 то векторы
то векторы 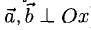 ).
).
7°. Система векторов 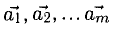 называется линейно независимой, если равенство
называется линейно независимой, если равенство
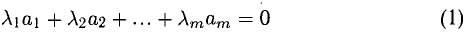
( 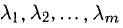 — действительные числа) возможно только при
— действительные числа) возможно только при  Если же равенство (1) возможно при некотором нетривиальном наборе
Если же равенство (1) возможно при некотором нетривиальном наборе 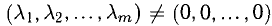 то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 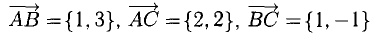 (рис. 3.4).
(рис. 3.4).
Найдем длины сторон: 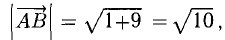
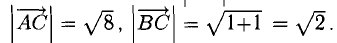
Нетрудно видеть, что 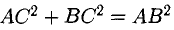 Следовательно, треугольник ABC прямоугольный с гипотенузой
Следовательно, треугольник ABC прямоугольный с гипотенузой 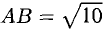 и катетами
и катетами 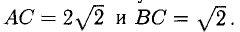
Пример:
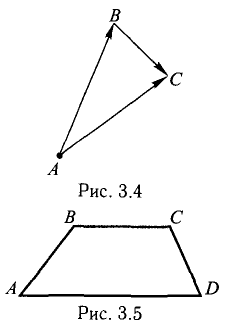
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
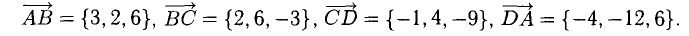
Имеем 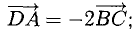 значит, ABCD — трапеция.
значит, ABCD — трапеция.
Пример:
Найти орт и направляющие косинусы вектора 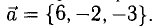
Решение:
Имеем 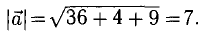 В соответствии с п. 3°, 4°
В соответствии с п. 3°, 4°
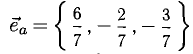 и направляющие косинусы вектора
и направляющие косинусы вектора 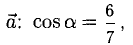
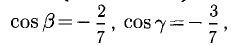 причем
причем 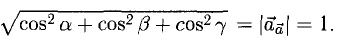
Пример:
Определить точку В, которая является концом вектора 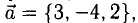 , если его начало совпадает с точкой
, если его начало совпадает с точкой
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
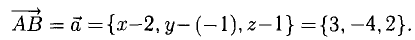
Следовательно, 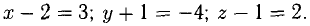 Ответ. В(5, -5,3).
Ответ. В(5, -5,3).
Пример:
Вектор 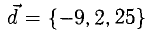 разложить по векторам
разложить по векторам
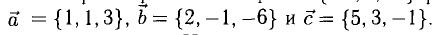
Решение:
Необходимо найти такие числа х, у, z, что 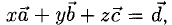 т.е.
т.е.
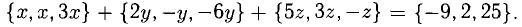
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
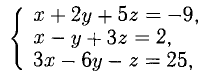
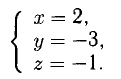
Ответ. 
Пример:
Показать, что система векторов 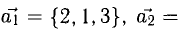
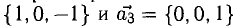 линейно независима.
линейно независима.
Решение:
В данном случае равенство (1) имеет вид 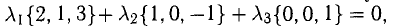 , или
, или 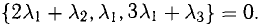 Отсюда получаем систему уравнений
Отсюда получаем систему уравнений
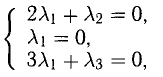
из которой следует, что 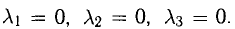 Это подтверждает линейную независимость данных векторов.
Это подтверждает линейную независимость данных векторов.
Пример:
Показать, что система векторов 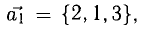
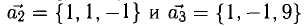 линейно зависима.
линейно зависима.
Решение:
Равенство (1) равносильно системе уравнений
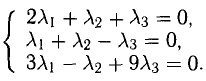
Она имеет ненулевое решение, например, 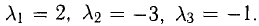 Таким образом,
Таким образом, 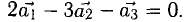 Отсюда видно, что
Отсюда видно, что 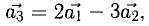 т.е. вектор
т.е. вектор 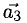 линейно выражается через
линейно выражается через 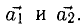 Очевидно, что
Очевидно, что 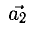 можно выразить через
можно выразить через 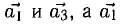 — через
— через 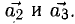
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 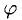 между ними:
между ними:
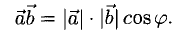
Из  (рис. 3.7) имеем
(рис. 3.7) имеем 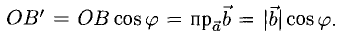 (
( 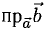 — проекция вектора
— проекция вектора 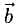 на направление вектора
на направление вектора  ).
).
Итак, 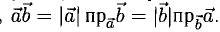
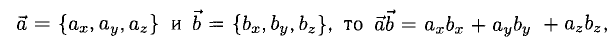
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 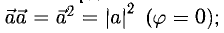 если же
если же 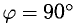 , т. е.
, т. е. 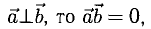 поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
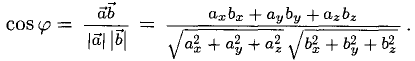
Примеры с решениями
Пример:
Перпендикулярны ли векторы 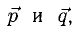 если
если 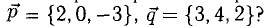
Решение:
Условие перпендикулярности векторов (п. 2°) 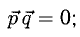 в нашем случае
в нашем случае
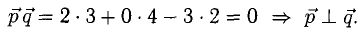
Пример:
Найти проекцию вектора 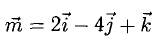 на направление вектора
на направление вектора 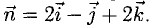
Решение:
Имеем 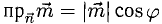 (п. 1°). Подставив сюда выражение для
(п. 1°). Подставив сюда выражение для 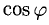 из п. 3°, получим
из п. 3°, получим
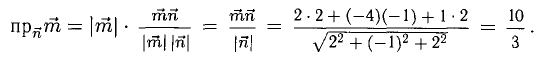
Ответ 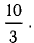
Пример:
Зная векторы, совпадающие с двумя сторонами:  и
и 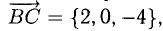 найти внутренние углы треугольника ABC.
найти внутренние углы треугольника ABC.
Решение:
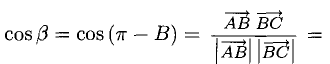
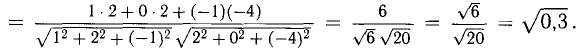
При помощи таблиц находим 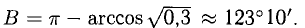 Для нахождения других углов нам понадобится вектор
Для нахождения других углов нам понадобится вектор 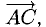 который является суммой
который является суммой 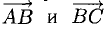 :
: 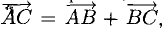 поэтому
поэтому 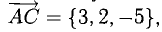
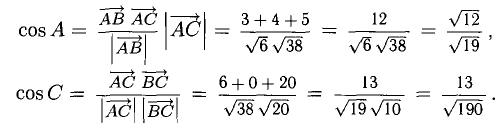
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
Найти координаты вектора  если
если  где
где  и
и 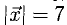
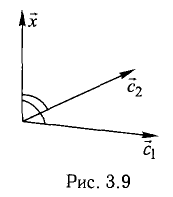
Решение:
На рис. 3.9 имеем 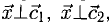 Из условий перпендикулярности векторов (п. 2°) имеем
Из условий перпендикулярности векторов (п. 2°) имеем 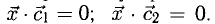 Положим
Положим  Условие задачи перепишем в виде Рис. 3.9 системы
Условие задачи перепишем в виде Рис. 3.9 системы
Векторное произведение векторов
1°. Векторы  приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора
приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора  на плоскость векторов
на плоскость векторов 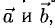 то кратчайший поворот от
то кратчайший поворот от 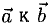 совершается против (по) часовой стрелки (рис. 3.10).
совершается против (по) часовой стрелки (рис. 3.10).
2°. Векторным произведением ненулевых векторов  называется вектор
называется вектор 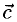 , обозначаемый
, обозначаемый 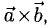 удовлетворяющий следующим трем условиям.
удовлетворяющий следующим трем условиям.
1) 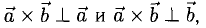 вектор
вектор 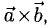 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 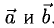
2) Вектор 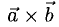 направлен так, что векторы
направлен так, что векторы 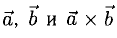 образуют правую тройку.
образуют правую тройку.
3) 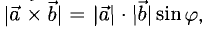 т.е. его длина численно равна площади параллелограмма, построенного на векторах
т.е. его длина численно равна площади параллелограмма, построенного на векторах 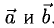 (рис. 3.11), таким образом,
(рис. 3.11), таким образом, 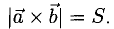
Если векторы 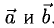 коллинеарны, то под
коллинеарны, то под 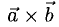 понимается нулевой вектор:
понимается нулевой вектор: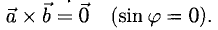
3°. Если известны координаты векторов-сомножителей 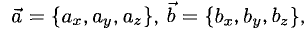 то для отыскания координат векторного произведения служит формула
то для отыскания координат векторного произведения служит формула
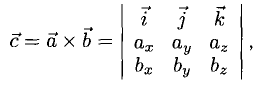
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В<3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 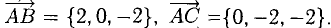 Определим координаты векторного произведения
Определим координаты векторного произведения 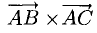 (рис. 3.12):
(рис. 3.12):
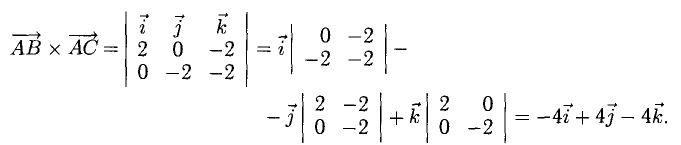
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 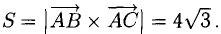 Площадь треугольника
Площадь треугольника  равна
равна 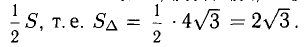
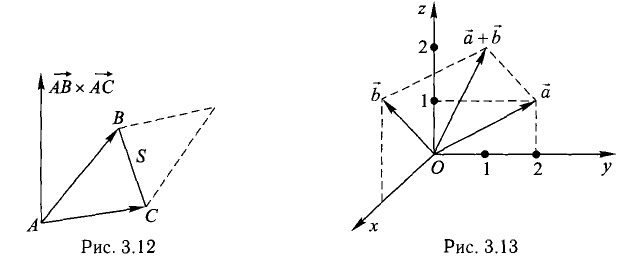
Пример:
Построить параллелограмм на векторах 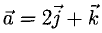 и
и 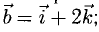 вычислить его площадь и высоту, опущенную на
вычислить его площадь и высоту, опущенную на  .
.
Сделаем чертеж (рис. 3.13). Имеем 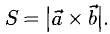 Отдельно вычисляем векторное произведение:
Отдельно вычисляем векторное произведение:
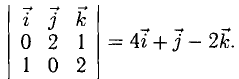
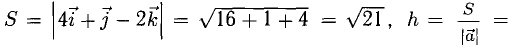
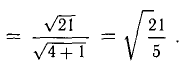
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов  называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение
называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение 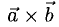 , а другой — вектор
, а другой — вектор 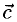 . Обозначение:
. Обозначение: 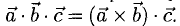 Если
Если  образуют правую тройку, то
образуют правую тройку, то 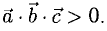 Если
Если  образуют левую тройку, то
образуют левую тройку, то 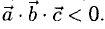
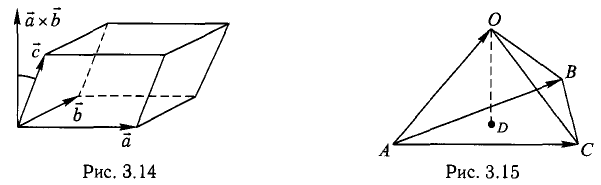
Модуль смешанного произведения векторов  равен объему параллелепипеда (рис. 3.14), построенного на этих векторах,
равен объему параллелепипеда (рис. 3.14), построенного на этих векторах, 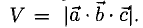 Условие
Условие 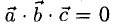 равносильно тому, что векторы
равносильно тому, что векторы  расположены в одной плоскости, т.е. компланарны. Имеет место равенство
расположены в одной плоскости, т.е. компланарны. Имеет место равенство
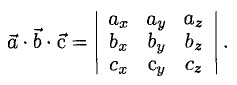
Объем тетраэдра с вершинами в точках 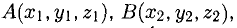
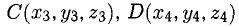 можно вычислить по формуле
можно вычислить по формуле 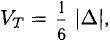 где
где
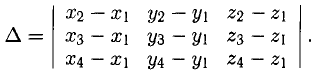
2°. Условие 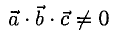 равносильно условию линейной независимости
равносильно условию линейной независимости  , а тогда любой вектор
, а тогда любой вектор 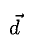 линейно выражается через них, т. е.
линейно выражается через них, т. е. 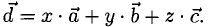 Для определения х, у, z следует решить соответствующую систему линейных уравнений
Для определения х, у, z следует решить соответствующую систему линейных уравнений
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах 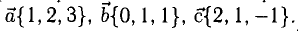
Решение:
Искомый объем 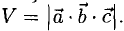 Поскольку
Поскольку
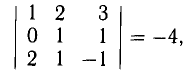
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 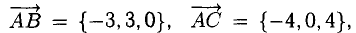
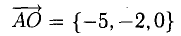 .Объем пирамиды ОАВС (тетраэда) равен
.Объем пирамиды ОАВС (тетраэда) равен
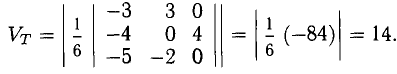
3) Площадь грани ABC
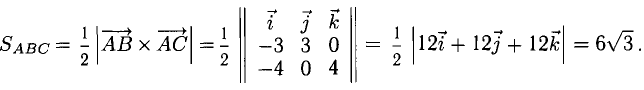
4) Объем пирамиды 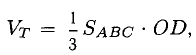 отсюда
отсюда 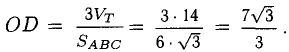
Ответ. 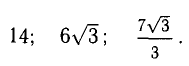
Основные понятия векторной алгебры




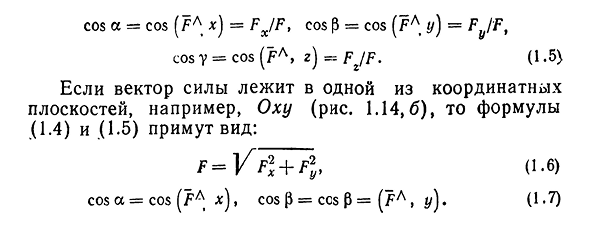
Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси  некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
Пусть М — произвольная точка оси  . Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).
. Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).

Оnределение:
Ось  с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
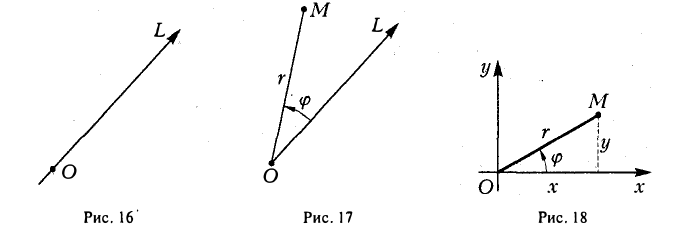
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
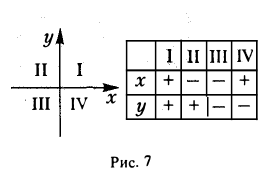
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:

Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
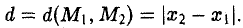
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
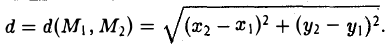
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
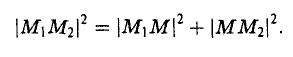
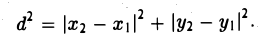
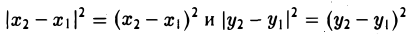
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 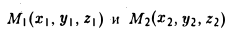 в пространстве вычисляется по следующей формуле
в пространстве вычисляется по следующей формуле
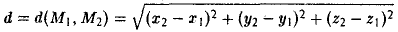
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
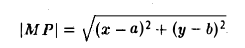
и возведем обе части полученного равенства в квадрат:
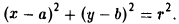
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
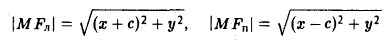
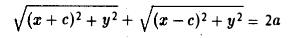
Перенесем второй корень в правую часть
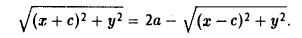
Возводя обе части в квадрат, после простых преобразований получим
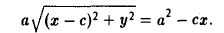
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
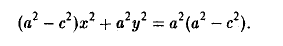
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b 2 , nолучаем уравнение эллипса
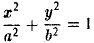
Деление отрезка в данном отношении:
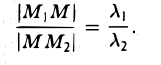
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
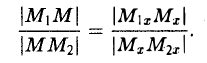
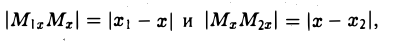
то из последних двух соотношений получаем, что
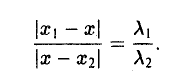
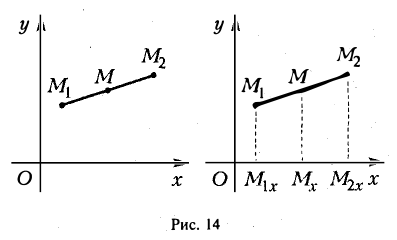
Точка М лежит между точками М1 и М2 , поэтому либо х 1 х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
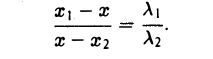

В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
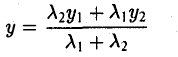
доказывается аналогичным рассуждением .
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
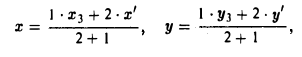
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
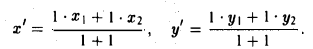
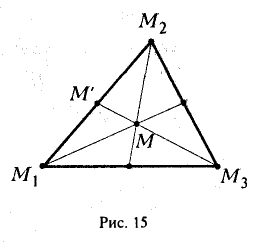
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
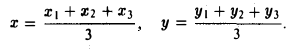
Замечание:
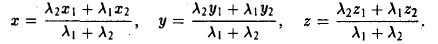
Полярные координаты
Предположим, что задана точка О, ось  .содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
.содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси  и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
Точка О называется полюсом,  — полярной осью.
— полярной осью.
Ясно, что Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный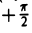 . Тогда
. Тогда
(рис.18). В свою очередь 
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г, 
Определители 2-го и 3-го порядков
Определителем второго порядка называется число
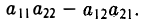
Обозначение:
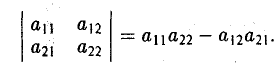
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
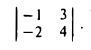
По правилу (1) имеем
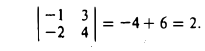
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
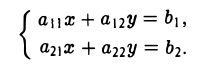
Решая эту систему методом исключения неизвестных при условии, что
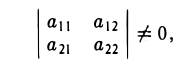
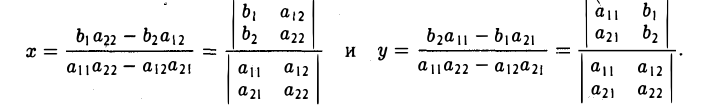
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом

и вычисляемое по следующему правилу:
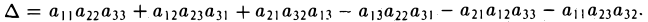
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
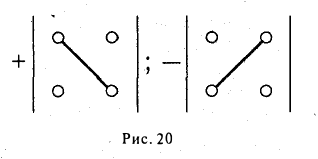
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
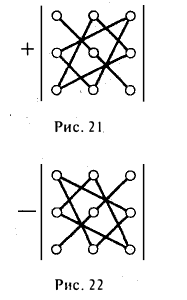
Пример:

Применяя правило треугольника, находим
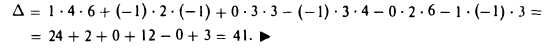
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
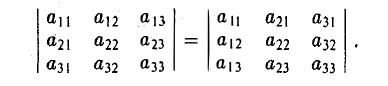
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
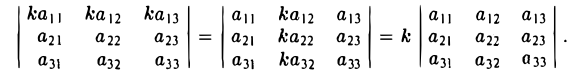
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка

Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
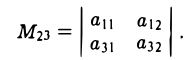
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
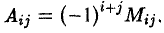
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
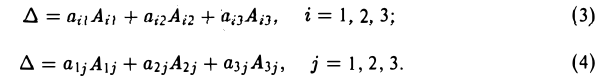
Покажем, например, что
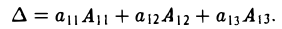
Пользуясь формулой (2), получаем, что
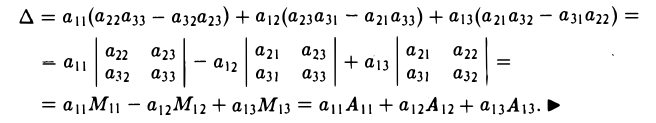
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
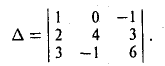
Раскладывая определитель по элементам 1-ой строки, получим
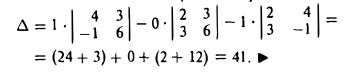
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор  однозначно определяется заданием связанного вектора АВ.
однозначно определяется заданием связанного вектора АВ.
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой
 = а
= а
(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 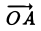 = а. От полученной точки А отложим вектор b:
= а. От полученной точки А отложим вектор b:  = b. Полученный в результате вектор
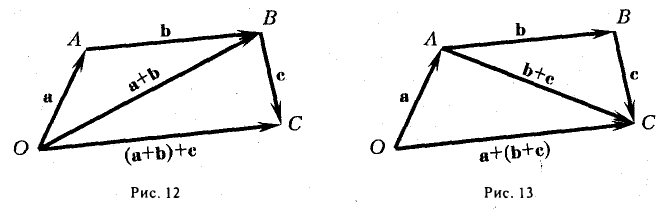
= b. Полученный в результате вектор  называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
а + b = b + а
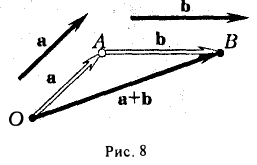
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор  , идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
, идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
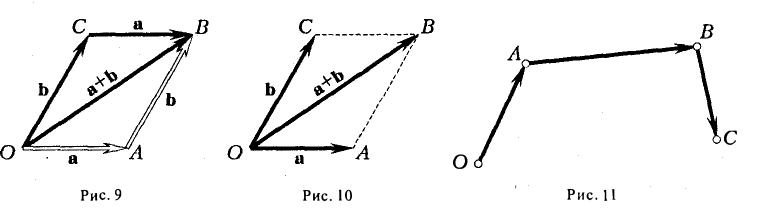
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a:  = а; от полученной точки А отложим вектор b:
= а; от полученной точки А отложим вектор b:  = b; отточки В — вектор с:
= b; отточки В — вектор с: 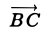 = с (рис. 11). По определению суммы
= с (рис. 11). По определению суммы  — а + b и
— а + b и  = (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
= (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
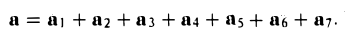
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
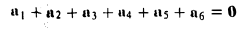
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О,  = n,
= n,  = Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
= Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ 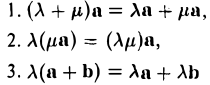
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
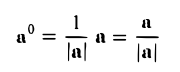
есть единичный вектор (орт) направления вектора а (рис. 18).
Координаты и компоненты вектора
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что

Векторы 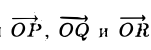 коллинеарны соответственно единичным векторам i, j, k,
коллинеарны соответственно единичным векторам i, j, k,
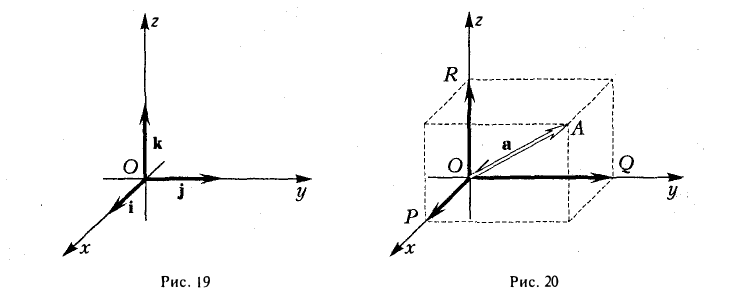
поэтому найдутся числа х, у, z такие, что
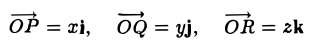
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = <х, y,z>.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = < х1, у1, z1 > и b = <х2, у2, z2> равны тогда и только тогда, когда соответственно равны их координаты, т. е.
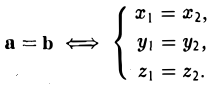
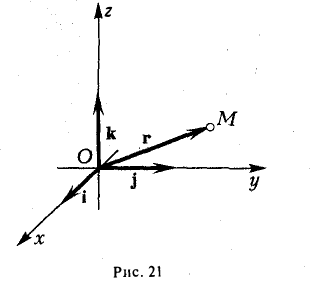
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
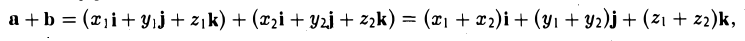
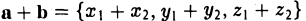
— при сложении векторов их координаты попарно складываются. Аналогично получаем
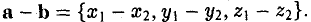
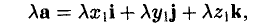
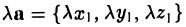
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = < х1, у1, z1>, b = < х2, у2, z2 > — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
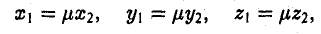
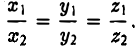
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
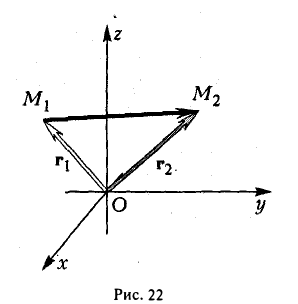
Пример:
Найти координаты вектора 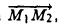 начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
Из рис. 22 видно, что 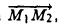 = r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
= r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
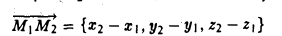
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
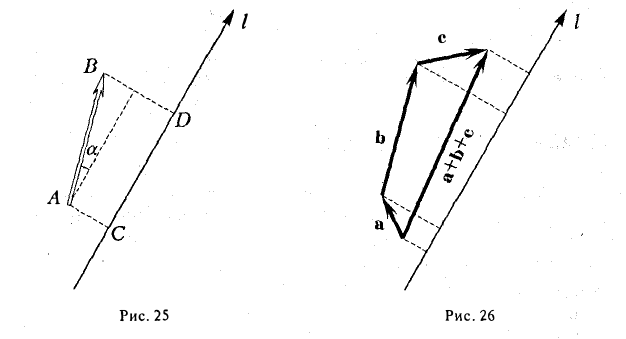
Проекция вектора на ось
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор  , определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
, определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
Определение:
Проекцией вектора  на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
Обозначение: 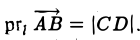
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
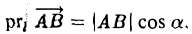
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
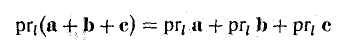
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
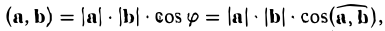
(1)
где φ, или в иной записи ( ), есть угол между векторами а и b (рис. 27 а).
), есть угол между векторами а и b (рис. 27 а).
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
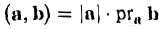
(рис. 27 б) и, аналогично,’ (2)
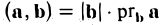
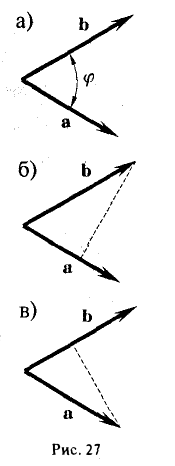
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
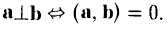
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
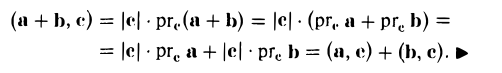
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
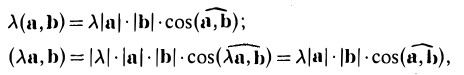
поскольку при λ > 0 углы (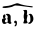 ) и (λ
) и (λ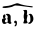 ) равны (рис.28).
) равны (рис.28).
Аналогично рассматривается случай λ 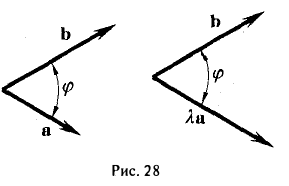
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
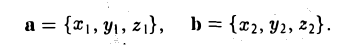
Рассмотрим скалярное произведение векторов а и b:
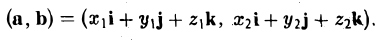
Пользуясь распределительным свойством скалярного произведения, находим
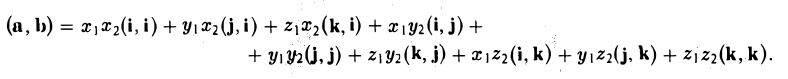
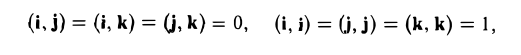
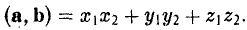
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а 2 .
Применяя формулу (4) при b = а, найдем (5)
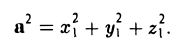
С другой стороны,
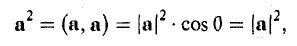
так что из (5) следует, что (6)
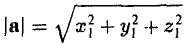
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
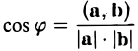
(предполагается, что векторы а и b — ненулевые).
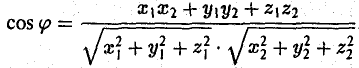
Пример:
Найти угол между векторами a = <2, -4,4,>и d = <-3,2,6>. Пользуясь формулой (8), находим
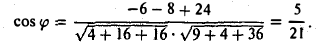
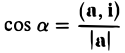
или, в координатной записи, (9)
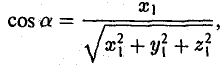
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
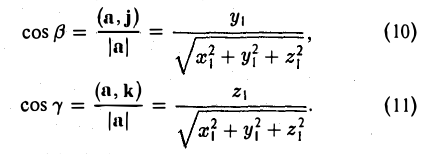
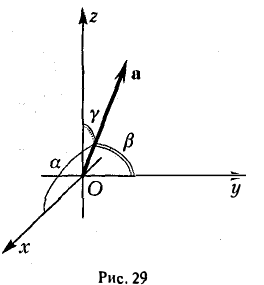
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
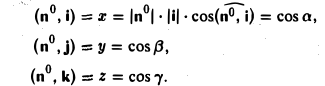
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
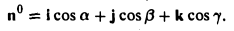
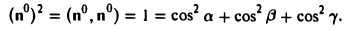
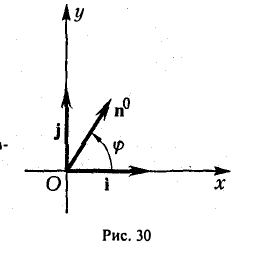
Пример:
Пусть единичный вектор n° ортогонален оси z:
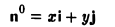
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
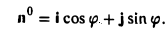
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
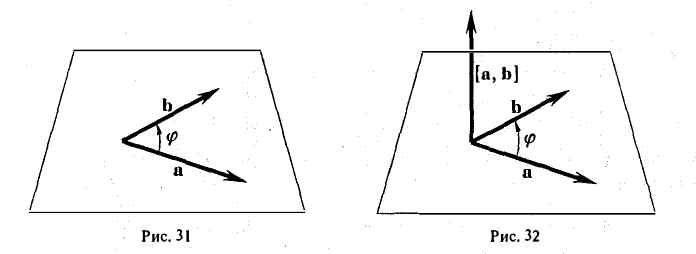
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
По определению длина векторного произведения (1)
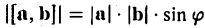
численно равна площади  параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
|[a, b]| =  .
.
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
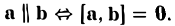
2. Векторное произведение антикоммутативно, т. е. всегда (2)
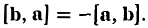
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = < х1, у1, z1>, b = < х2, у2, z2 >. Пользуясь распределительным свойством векторного произведения, находим (3)
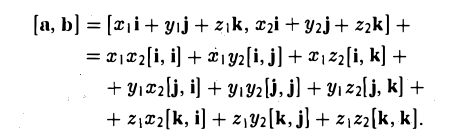
Выпишем векторные произведения координатных ортов (рис. 35):
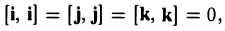
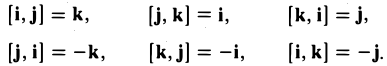
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
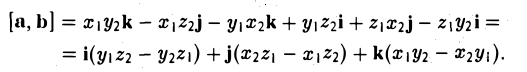
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
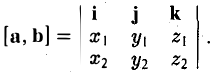
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 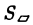 = |[а, b]. Поэтому находим
= |[а, b]. Поэтому находим
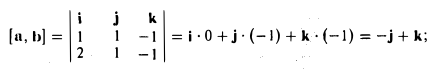
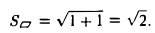
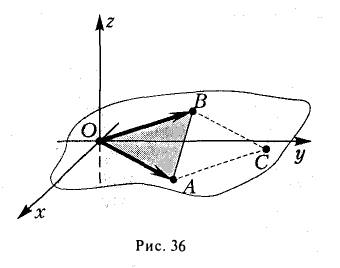
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= 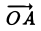 и b =
и b =  , получаем
, получаем
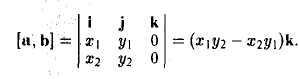
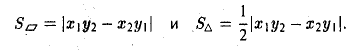
Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
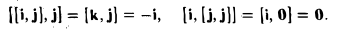
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
Геометрический смысл смешанного произведения
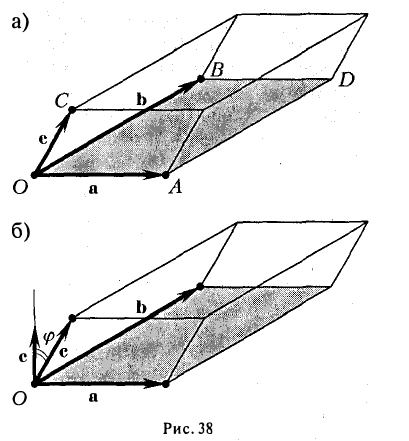
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
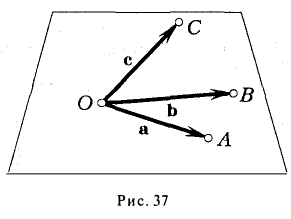
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где  — площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
— площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
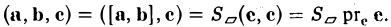
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
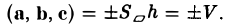
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
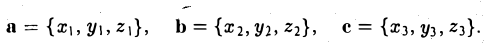
Найдем выражение для их смешанного произведения (а, b, с). Имеем
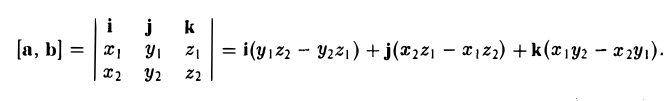
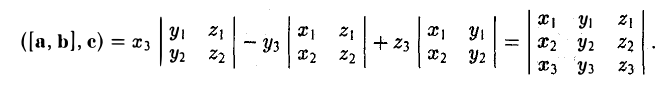
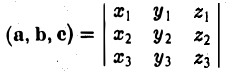
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
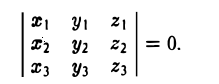
Пример:
Проверить, компланарны ли векторы
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
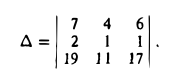
Разлагая его по элементам первой строки, получим
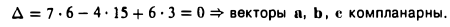
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://ru1.warbletoncouncil.org/vectores-unitarios-9631
http://lfirmal.com/vektornaya-algebra-osnovnyie-ponyatiya-i-opredeleniya/
[/spoiler]
1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы ![]() и
и ![]() ,
, ![]() и противоположно направленные им векторы, например:
и противоположно направленные им векторы, например:
![]()
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам ![]() .
.
А теперь рассмотрим произвольный вектор ![]() либо
либо
![]() и поставим задачу найти
и поставим задачу найти
единичный вектор ![]() , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора
, коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора ![]() разделить на его длину:
разделить на его длину:
![]() либо
либо ![]() ,
,
или, что то же самое – умножить каждую координату вектора ![]() на
на ![]() . То
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
![]() либо
либо ![]()
Задача 10
Найти единичные векторы, коллинеарные векторам а) ![]() , б)
, б) ![]() . Выполнить проверку.
. Выполнить проверку.
Решение: а) вычислим длину вектора ![]() и найдём
и найдём
сонаправленный единичный вектор:
![]() , от иррациональности в знаменателе (корня) тут
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
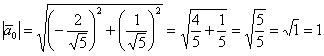 , что и требовалось проверить.
, что и требовалось проверить.
Второй вектор очевиден: ![]() , как очевидна и его
, как очевидна и его
длина ![]() .
.
Ответ: ![]()
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.
 1.5.6. Деление отрезка в данном отношении
1.5.6. Деление отрезка в данном отношении
 1.5.4. Действия с векторами в координатах
1.5.4. Действия с векторами в координатах
| Оглавление |
Автор: Aлeксaндр Eмeлин
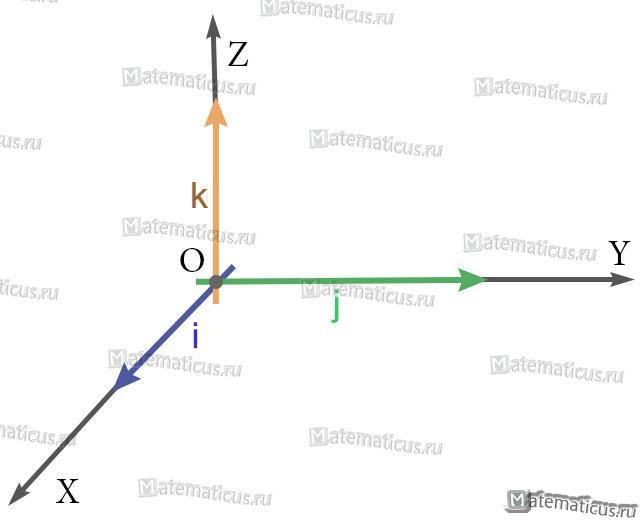
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0);j(0;1;0); k(0;0;1);
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
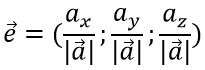
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$left| {vec a} right| = sqrt {{1^2} + {2^2} + {{left( { — 2} right)}^2}} = 3$
затем вычисляем единичный вектор e
$vec e = left( {frac{1}{3};frac{2}{3}; — frac{2}{3}} right)$
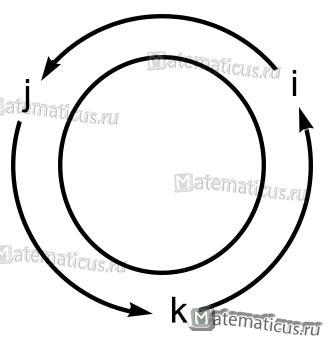
Векторное произведения единичных векторов
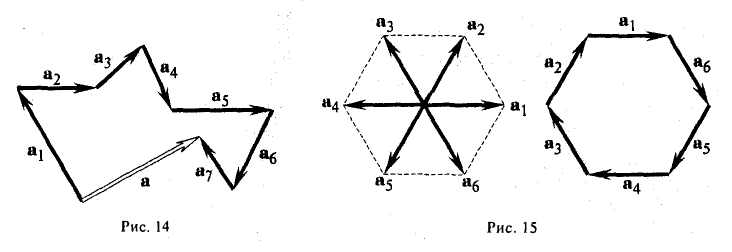
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.

Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
i×i=0 i×j=k i×k=-j
j×i=-k j×j=0 j×k=i
k×i=j k×j=-i k×k=0
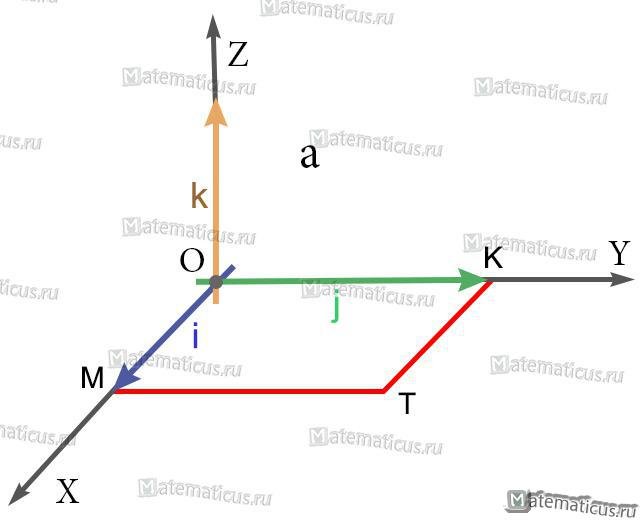
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
![]() 20573
20573
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Определение
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
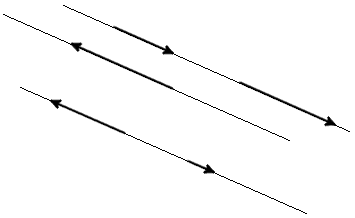
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
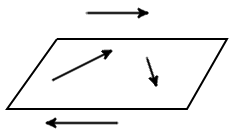
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать 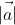 .
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор 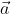 имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора 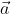 , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор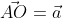 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
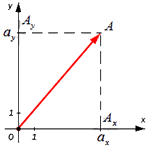
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
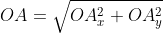
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 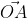 получаем
получаем
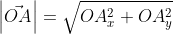
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
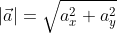
Когда вектор 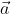 дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 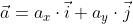 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле 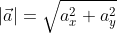 , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Пример
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Необходимо:
Чтобы найти модуль вектора используем ранее приведённую формулу
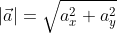
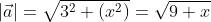
Ответ: 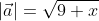
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор 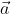 =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a )
)
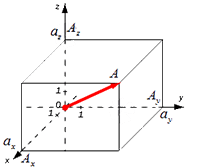
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому
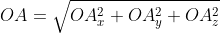
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
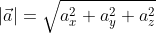
Пример
Необходимо узнать длину вектора ( left|vec{a}right|=2*vec{i}+3*vec{j}+4*vec{k} ), в котором ( vec{i}, vec{j}, vec{k} ), орты.
Решение
Получается, что дан вектор ( left|vec{a}right| ) с координатами (2; 3; 4)
Применив выведенную ранее формулу получим
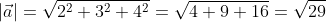
Ответ: 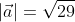
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор 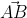 имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
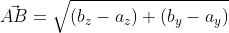
При этом формула вычисления длины вектора 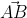 для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 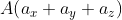 и
и 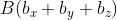 ), будет следующей:
), будет следующей:
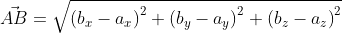
Пример
Для прямой системы координат, найти длину вектора ( overrightarrow{AB}) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
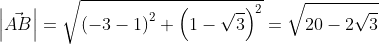
Существует второй вариант решения, где формулы применяются по очереди:
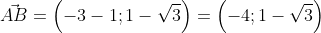
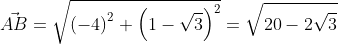
Ответ: 
Пример
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
Решение
В первую очередь представим длину вектора в виде формулы.
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
(=sqrt{left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2} = sqrt{26 + left ( lambda^2 -2right )^2})
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
(
sqrt{26+left(lambda^2-2right)^2}=sqrt{30}
)
(
26+left(lambda^2-2right)^2=30
)
(
left(lambda^2-2right)^2=4
)
(
lambda^2-2=2
)
или
(
lambda^2-2=-2
)
(
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Ответ: (
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow{AB}) и (overrightarrow{AC}) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow{BC} ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Пример
Даны длины двух векторов ( overrightarrow{AK}) и ( overrightarrow{AM}) 2 и 4 соответственно, а угол между ними равен ( frac{pi}{3} ) . необходимо найти длину ( overrightarrow{KM}).
Решение
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
(
KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac{pi}{3})
(=2^2+4^2-2cdot2cdot4cdotcosfrac{pi}{3})
(=4+16-16cosfrac{pi}{3})
(=20-8=12
)
Получается (KM=sqrt{12}
)
Ответ: (
left|overrightarrow{KM}right|=sqrt{12}
)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
Первая формула это ( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2}. ), для плоскости
( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2+a_z^2} )
длина вектора формула для трёхмерного пространства;
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vec{AB}right|=sqrt{left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2}) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vec{S}right|=sqrt{ s_x^2+s_y^2}) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
Все курсы > Линейная алгебра > Занятие 1
Материалы по линейной алгебре используют определения и примеры следующих курсов и источников:
- 3Blue1Brown⧉
- Khan Academy: Linear Algebra⧉
- Linear Algebra⧉, PCA⧉, ICL
- Linear Algebra⧉, MIT
- Matrix Methods for Data Analysis and Machine Learning⧉, MIT
- Matrix Algebra for Engineers⧉
- Introduction to Linear Algebra, Gilbert Strang
- Mathematics for Machine Learning, Marc Peter Deisenroth
На первом занятии мы более подробно познакомимся с понятием вектора и векторного пространства.
Ноутбук к сегодняшнему занятию⧉
Понятие вектора
Вектор (vector) — это направленный отрезок, и для нас будет важно, что любой вектор обладает длиной (magnitude) и направлением (direction). Например, возьмем вот такой двумерный вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
На курсе мы будем обозначать векторы полужирной строчной буквой, например $textbf{v}$, а матрицы заглавной буквой, например, А.
Вектор $textbf{v}$ удобно изобразить на координатной плоскости, исходящим из начала координат.
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([0, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |
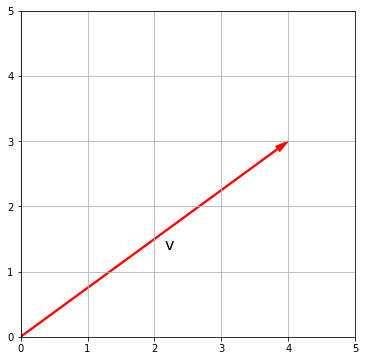
Добавлю, что вектор — частный случай матрицы. В случае вектор-столбца речь идет о матрице размерностью n x 1. В случае вектор-строки — 1 x n. Вектор $textbf{v}$ — это матрица 2 х 1.
Операции над векторами
Сложение векторов
Складывать векторы очень несложно. Достаточно сложить их компоненты или координаты.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + begin{bmatrix} 2 \ -1 end{bmatrix} = begin{bmatrix} 6 \ 2 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, –1]) a_plus_b = a + b a_plus_b |
Графически, если поставить начало второго вектора в конец первого, сложение можно представить как расстояние от начала первого вектора до конца второго. Своего рода путь, пройденный двумя векторами.
|
ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_a_plus_b = ax.arrow(0, 0, a_plus_b[0], a_plus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b, arrow_a_plus_b], [‘вектор a’, ‘вектор b’, ‘вектор a + b’], prop = {‘size’: 16}) plt.show() |
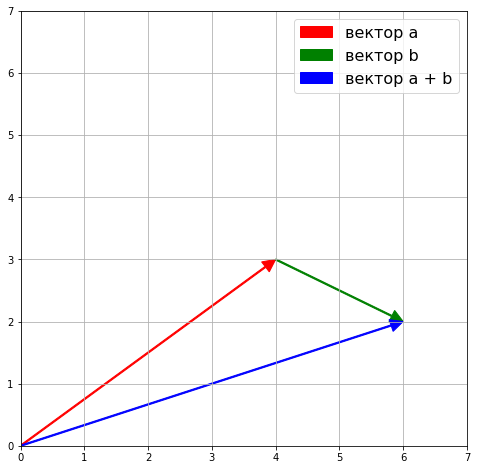
Сложение векторов ассоциативно $textbf{a} + textbf{b} = textbf{b} + textbf{a}$.
Умножение на скаляр
Умножение на скаляр просто удлиняет или укорачивает вектор.
$$ 2 cdot textbf{v} = 2 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} 8 \ 6 end{bmatrix} $$
|
v = np.array([4, 3]) double_v = 2 * v double_v |
|
ax = plt.axes() plt.xlim([0, 10]) plt.ylim([0, 10]) plt.grid() ax.arrow(0, 0, double_v[0], double_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘2v’, xy=(double_v[0], double_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |

Умножение на отрицательное число не только удлиняет или укорачивает вектор, но и переворачивает его направление.
$$ -0,5 cdot textbf{v} = -0,5 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -2 \ -1,5 end{bmatrix} $$
|
v = np.array([4, 3]) neg_half_v = –0.5 * v neg_half_v |
|
ax = plt.axes() plt.xlim([–5, 5]) plt.ylim([–5, 5]) plt.grid() ax.arrow(0, 0, neg_half_v[0], neg_half_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-0.5v’, xy=(neg_half_v[0], neg_half_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |

Очевидно, что умножение на −1 просто переворачивает направление вектора, но не меняет его длины.
$$ -1 cdot textbf{v} = -1 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -4 \ -3 end{bmatrix} $$
|
v = np.array([4, 3]) neg_one_v = –1 * v neg_one_v |
|
ax = plt.axes() plt.xlim([–5, 5]) plt.ylim([–5, 5]) plt.grid() ax.arrow(0, 0, neg_one_v[0], neg_one_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-v’, xy=(neg_one_v[0], neg_one_v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) plt.show() |

Вычитание и деление на число
Вычитание векторов можно представить как сумму первого вектора со вторым вектором, умноженным на −1.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + left( -1 cdot begin{bmatrix} 2 \ -1 end{bmatrix} right) = begin{bmatrix} 2 \ 4 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, –1]) b_neg = –1 * b a_minus_b = a + b_neg b_neg, a_minus_b |
|
(array([-2, 1]), array([2, 4])) |
Графически мы сначала находим вектор $textbf{-b}$ (зеленая стрелка), а затем прибавляем его к вектору $textbf{a}$ (красная стрелка).
|
plt.figure(figsize = (8, 8)) ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b_neg = ax.arrow(a[0], a[1], b_neg[0], b_neg[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.0001, head_width = 0.1, head_length = 0.1, length_includes_head = True, fc = ‘black’, ec = ‘black’, linestyle = ‘–‘) arrow_a_minus_b = ax.arrow(0, 0, a_minus_b[0], a_minus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b_neg, arrow_b, arrow_a_minus_b], [‘вектор a’, ‘вектор -b’, ‘вектор b’, ‘вектор a+(-b)’], prop = {‘size’: 16}) plt.show() |

Остается добавить, что деление вектора на число, это всего лишь умножение на обратное число (multiplicative inverse). Разделим вектор $textbf{v}$ на семь.
$$ frac{textbf{v}}{7} = begin{bmatrix} 4 \ 3 end{bmatrix} cdot frac{1}{7} = begin{bmatrix} frac{4}{7} \ frac{3}{7} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/7) |
|
array([0.57142857, 0.42857143]) |
Тот факт, что мы выразили вычитание через сложение и умножение на скаляр, а деление через умножение на обратное число позволило нам остаться в пределах операций сложения и умножения на скаляр.
Видео про векторы⧉.
Длина вектора
Длину или норму вектора (norm, length, magnitude or size of a vector) рассчитать не сложно, достаточно вспомнить теорему Пифагора. Снова возьмем вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([–0.01, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.hlines(y = 0, xmin = 0, xmax = 4, linewidth = 3, color = ‘b’, linestyles = ‘–‘) ax.vlines(x = 4, ymin = 0, ymax = 3, linewidth = 3, color = ‘g’, linestyles = ‘–‘) plt.show() |

Как видно на графике, вектор $textbf{v}$, смещение вдоль оси x и смещение вдоль оси y образуют прямоугольный треугольник. Значит, длина вектора (гипотенуза) равна квадратному корню из суммы квадратов смещений (катетов или в нашем случае координат).
$$ ||textbf{v}|| = sqrt{4^2 + 3^2} = sqrt{25} = 5 $$
Для n-мерного вектора ничего не меняется.
$$ ||textbf{v}|| = sqrt{v_1^2 + v_2^2 + dots + v_n^2} $$
Например, найдем длину трехмерного вектора $textbf{w}$.
$$ textbf{w} = begin{bmatrix} 6 \ 3 \ 2 end{bmatrix} rightarrow ||textbf{w}|| = sqrt{6^2 + 3^2 + 2^2} = sqrt{49} = 7 $$
Единичный вектор
Вектор с длиной, равной единице, называют единичным вектором (unit vector). Примерами единичных векторов, с которыми мы будем часто встречаться в пространстве $ R^2 $, являются следующие два вектора
$$ hat{i} = begin{bmatrix} 1 \ 0 end{bmatrix}, hat{j} = begin{bmatrix} 0 \ 1 end{bmatrix} $$
Единичный вектор принято обозначать строчной буквой с знаком циркумфлекса, «крышечки» (hat).
Проверим, равна ли их длина единице.
$$ ||hat{i}|| = sqrt{1^2 + 0^2} = sqrt{1} = 1, ||hat{j}|| = sqrt{0^2 + 1^2} = sqrt{1} = 1 $$
Интересно, что с помощью векторов $ hat{i}, hat{j} $ можно выразить любой другой вектор в $ R^2 $. Например, вектор $textbf{v}$ можно представить как
$$ 4 begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 4 \ 3 end{bmatrix} rightarrow 4hat{i} + 3 hat{j} $$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
v = np.array([4, 3]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([–0.07, 4.5]) plt.ylim([–0.07, 4.5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, –10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
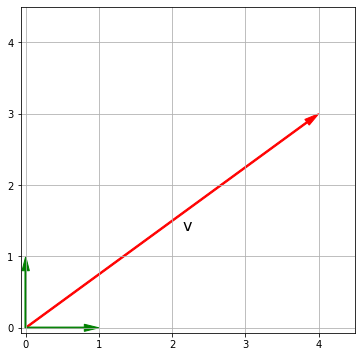
Это обстоятельство нам пригодится в будущем.
Нормализация вектора
Длина нормализованного вектора равна единице. Для того чтобы нормализовать вектор, достаточно разделить вектор на его длину. Создадим единичный вектор $hat{v}$ для вектора $textbf{v}$.
$$ hat{v} = frac{textbf{v}}{||textbf{v}||} = frac{1}{5} cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} frac{4}{5} \ frac{3}{5} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/np.linalg.norm(v)) |
Скалярное произведение
Важной операцией над векторами является уже знакомое нам скалярное произведение (dot product). В качестве напоминания того, как работает скалярное произведение приведем несложный пример. Пусть даны два вектора $textbf{v}$ и $textbf{w}$.
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 2 \ 1 end{bmatrix} $$
Найдем их скалярное произведение.
$$ textbf{v} cdot textbf{w} = 4 cdot 2 + 3 cdot 1 = 11 $$
Как вы видите, мы перемножаем компоненты векторов и складываем получившиеся произведения.
Скалярное произведение как длина вектора
Интересно, что корень из скалярного произведения вектора на самого себя есть его длина.
$$ sqrt{ textbf{v} cdot textbf{v} } = sqrt{4 cdot 4 + 3 cdot 3 } = sqrt{ 4^2 + 3^2 } = sqrt{25} = 5 $$
|
v = np.array([4, 3]) np.sqrt(v.dot(v)) |
Угол между векторами
Помимо этого скалярное произведение определяется как произведение длин векторов на косинус угла между ними.
$$ mathbf a cdot mathbf b = ||a|| cdot ||b|| cdot cos(theta) $$
Именно это свойство привело нас к расчету косинусного расстояния между векторами.
$$ cos(theta) = frac{mathbf a cdot mathbf b}{||a|| cdot ||b||} $$
Выведем эту формулу. Для начала вспомним теорему косинусов.
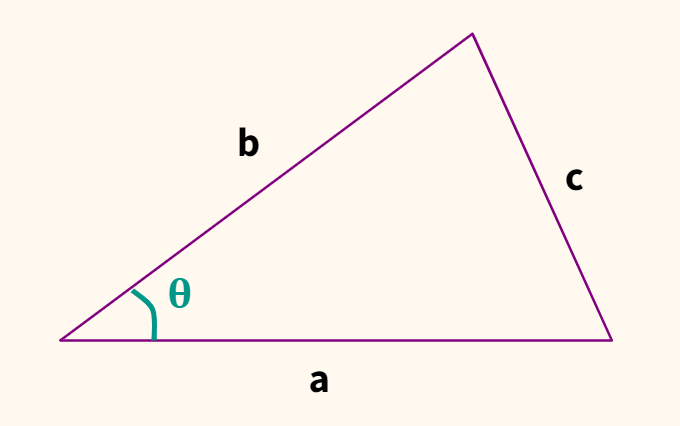
$$ c^2 = a^2 + b^2-2ab cdot cos(theta) $$
Теперь представим, что у нас не стороны треугольника, а векторы. Если сторону а обозначить как вектор $ textbf{a} $, сторону b — как вектор $ textbf{b} $, то сторона с станет разностью между $ textbf{a} $ и $ textbf{b} $. Чтобы убедиться в этом, найдите $ textbf{-b} $ и приставьте его к окончанию $ textbf{a} $.
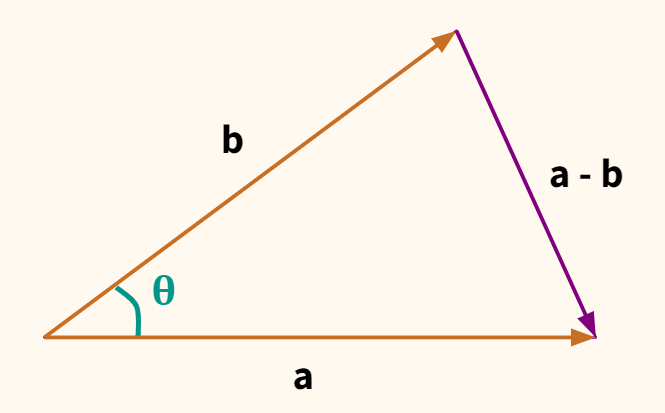
Выразим теорему косинусов через длины векторов.
$$ || a-b ||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Помня, что длина есть скалярное произведение вектора на самого себя, мы можем выразить левую часть $ || a-b || $ как
$$ (a-b)(a-b) = a cdot a-a cdot b-b cdot a + (-b) cdot (-b) = ||a||^2-2ab + ||b||^2 $$
Поместим результат в исходное выражение.
$$ ||a||^2-2ab + ||b||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Сократив подобные члены получим
$$ a cdot b = ||a|| cdot ||b|| cdot cos(theta) $$
Выводы. Из тригонометрии мы помним, что косинус 90 градусов равен нулю. Как следствие, скалярное произведение перпендиклярных (правильнее сказать ортогональных (orthogonal)) векторов $ textbf{a} perp textbf{b} $ равно нулю.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(90) = 0 $$
Очевидно, что если угол между двумерными векторами меньше 90 градусов, косинус, а значит и скалярное произведение положительны. В противном случае — отрицательны. Для n-мерных векторов положительное скалярное произведение говорит, что они в целом смотрят в одну строну, отрицательное — противоположные.
Для коллинеарных (сонаправленных) векторов скалярное произведение равно произведению их длин, потому что косинус нуля равен единице.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(0) = ||a|| cdot ||b|| $$
Добавлю, что если $ textbf{a} $ и $ textbf{b} $ — единичные векторы, то косинус угла между векторами просто равен его их скалярному произведению.
$$ cos(theta) = a cdot b $$
Рассчитаем косинусное расстояние для векторов
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 1 \ 7 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([1, 7]) numerator = np.dot(a, b) aLen = np.linalg.norm(a) bLen = np.linalg.norm(b) denominator = aLen * bLen cosine = numerator / denominator angle = np.arccos(cosine) * 360/2/np.pi cosine, angle |
|
(0.7071067811865475, 45.00000000000001) |
|
from scipy.spatial import distance 1 – distance.cosine([4, 3], [1, 7]) |
Внешнее произведение
Под внешним произведением (outer product) понимается умножение вектор-столбца на вектор-строку по обычным правилам матричного умножения. Результатом такого произведения будет матрица, а не число, как в случае скалярного произведения.

Ортогональность векторов
Еще раз продемонстрируем, почему если векторы ортогональны, их скалярное произведение будет равно нулю. Возьмем три вектора, образовывающих прямоугольный треугольник.

Тогда, по теореме Пифагора,
$$ || mathbf x ||^2 + || mathbf y ||^2 = || mathbf x + mathbf y ||^2 $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = (mathbf x + mathbf y)^T (mathbf x + mathbf y) $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + mathbf x^T mathbf y + mathbf y^T mathbf x $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + 2 mathbf x^T mathbf y $$
$$ mathbf 0 = 2 mathbf x^T mathbf y $$
$$ mathbf x^T mathbf y = mathbf 0 $$
Проекция вектора на вектор
Подойдем к скалярному произведению с другой стороны. Рассмотрим два вектора $ textbf{a} $ и $ textbf{b} $ и найдем проекцию первого вектора на второй.

Проекция через угол между векторами
Говоря неформально, проекцией вектора $ textbf{a} $ на вектор $ textbf{b} $ будет такой участок вектора $ textbf{b} $, что расстояние от точки A до точки B минимально. Минимальным оно будет, если угол OAB будет равен 90 градусов. Получается прямоугольный треугольник. Найдем отрезок OB.
$$ cos(theta) = frac {OB}{OA} = frac {OB}{||a||} rightarrow OB = ||a|| cdot cos(theta) $$
Выразим то же самое через формулу скалярного произведения, заменив $||a|| cdot cos(theta) $ на OB.
$$ b cdot a = ||b|| cdot ||a|| cdot cos(theta) rightarrow b cdot a = ||b|| cdot OB $$
Так мы нашли длину проекции OB. Ее называют числовой или скалярной проекцией (scalar projection).
$$ frac{b cdot a}{||b||} = ||a|| cdot cos(theta) = OB $$
Более того, если длина вектора $ textbf{b} $ равна единице, то длина проекции OB просто равна скалярному произведению.
$$ ||b|| = 1 rightarrow b cdot a = OB $$
Это объясняет, почему скалярное произведение еще называют projection product.
Очевидное и тем не менее интересное примечание. Обратите внимание на связь понимания скалярного произведения как проекции одного вектора на другой и произведения длин векторов на косинус угла между ними. Если векторы перпендикулярны, проекция одного вектора на другой равна нулю, а значит и произведение проекции второго вектора на первый равно нулю.

Предположим, нас интересует не только длина проекции, но и ее направление. В этом случае говорят про векторную проекцию (vector projection).
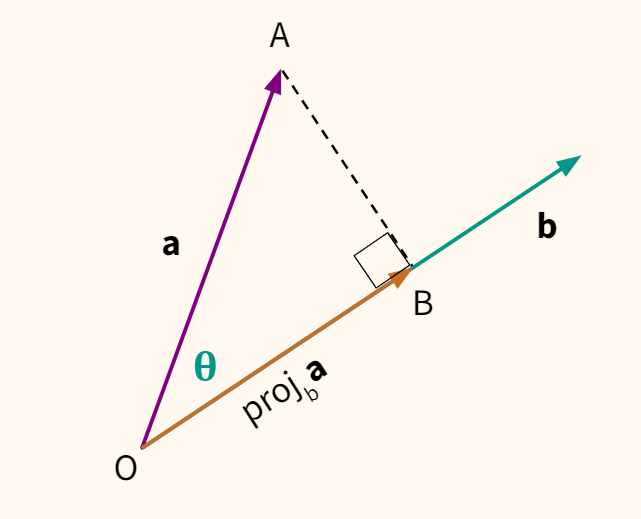
Она выражается как произведение нормализованного вектора $ textbf{b} $ на длину проекции (то есть скалярную проекцию) OB.
$$ proj_mathbf{b} textbf{a} = OB cdot hat{b} $$
Перепишем OB через скалярное произведение, а $hat{b}$ через частное вектора $ textbf{b} $ на его длину.
$$ proj_mathbf{b} textbf{a} = frac{b cdot a}{||b||} cdot frac{b}{||b||} $$
Таким образом, можно сказать, что векторная проекция показывает, длину вектора $ textbf{a} $ в направлении вектора $ textbf{b} $.
Пример. Возьмем два вектора a и b и найдем вначале скалярную, затем векторную проекцию вектора a на вектор b.
|
a = np.array([3, 4]) b = np.array([1, 1]) scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b |
|
vector_proj_a_on_b = scalar_proj_a_on_b * (b / np.linalg.norm(b)) vector_proj_a_on_b |
|
a = np.array([3, 4]) b = np.array([1, 1]) proj = np.array([3.5, 3.5]) ax = plt.axes() plt.xlim([–0.07, 4.5]) plt.ylim([–0.07, 4.5]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, proj[0], proj[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Матрица проекции
Векторную проекцию можно выразить с помощью матрицы проекции $P$.
$$ proj_mathbf{b} textbf{a} = P cdot mathbf a = frac{mathbf b mathbf b^T}{mathbf b^T mathbf b} cdot mathbf a $$
В знаменателе находится скалярное произведение и результатом умножения будет число. В числителе — внешнее произведение и результатом будет матрица. Найдем внешнее произведение из примера выше.
|
b_bT = np.outer(b, b) b_bT |
Найдем скалярное произведение.
Создадим матрицу проекции $P$ и умножим ее на вектор $mathbf a$.
Симметрия скалярного произведения
Продемонстрируем с точки зрения проекции, почему $a cdot b = b cdot a $. Возьмем два вектора a и b.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
a = np.array([1, 3]) b = np.array([4, 1]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([–0.07, 4]) plt.ylim([–0.07, 4]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.plot([0, 4], [0, 4], linestyle = ‘dashed’) plt.show() |
Выше мы сказали, что $ a cdot b = OB cdot ||b|| $. То есть скалярное произведение вектора a на вектор b равно произведению проекции a на b, умноженной на длину вектора b.
Продемонстрируем, что произведение проекции вектора a на вектор b, умноженное на длину вектора b, равно произведению проекции вектора b на вектор a, умноженному на длину вектора a.
$$ proj_ba times || b || = proj_ab times || a || $$
|
scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b * np.linalg.norm(b) |
|
scalar_proj_b_on_a = np.dot(b, a) / np.linalg.norm(a) scalar_proj_b_on_a * np.linalg.norm(a) |
|
np.dot(a, b), np.dot(b, a) |
Видео про скалярное произведение векторов⧉.
Векторное произведение
Векторное произведение (cross product) задано только в трехмерном пространстве. Результатом такого произведения будет вектор, перпендикулярный каждому из исходных векторов. Приведем иллюстрацию из Википедии⧉.

Математически векторное произведение задается формулой
$$ a times b = || a || || b || sin(theta) $$
Геометрически — это площадь параллелограмма, сформированного из исходных векторов a и b.

Приведем пример.
|
a = [1, 2, 3] b = [4, 5, 6] np.cross(a, b) |
Подведем итог
Сегодня мы ввели понятие вектора, познакомились с базовыми операциями с векторами, в частности, изучили скалярное произведение векторов и научились находить скалярную и векторную проекцию одного вектора на другой.
Перейдем к рассмотрению векторного пространства.
