Как найти длину электромагнитной волны по частоте

Длина, скорость и частота электромагнитной волны.

Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.

Электромагнитные колебания – это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.

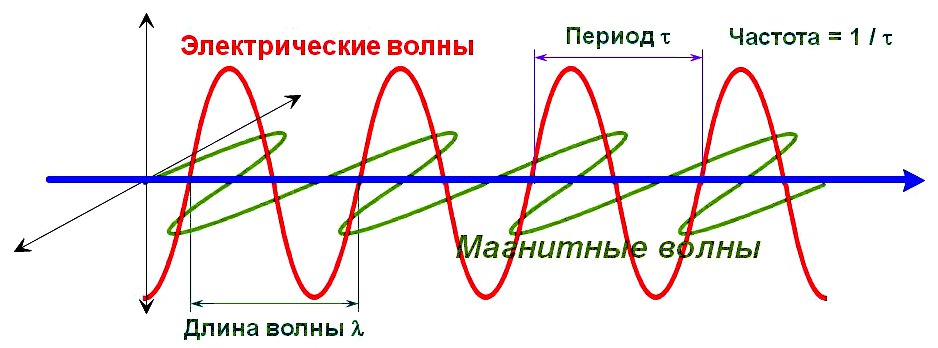
Рис.1

Длина волны, обозначаемая буквой λ и измеряемая в метрах –
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.

Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.

Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).

Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 – это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.

Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).

И окончательно для воздушной среды:

λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).

Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.

А теперь можно переходить к калькуляторам.

КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ

КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ

В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n – это, как мы помним, показатель преломления среды.
Другие, наоборот – как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду – если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.

Did this article help you?

Содержание:

• Определение и формула длины волны
• Длина стоячей волны
• Длина бегущей волны
• Длина бегущей волны
• Длина электромагнитной волны
• Единицы измерения длины волны
• Примеры решения задач

Определение и формула длины волны

Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:

$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$

где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.

Длина стоячей волны

Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):

$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$

где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:

$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$

Длина бегущей волны

В бегущей волне длина волны связана с фазовой скоростью (v_ph) формулой:

$$lambda=frac{v_{p h}}{nu}(4)$$

Длина бегущей волны

Разность фаз и длина волны

Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:

$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$

Длина электромагнитной волны

Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:

$$lambda=c T=frac{c}{nu}(6)$$

Длина электромагнитной волны в веществе равна:

$$lambda=frac{c}{n nu}(7)$$

где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.

Отметим, что все рассматриваемые формулы относят к случаю T=const.

Единицы измерения длины волны

Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м

В СГС: [$lambda$]=см

Примеры решения задач

Читать дальше: Формула количества теплоты.

Была ли эта статья полезной?

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе^[1][2].

Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π^[3].

Длину волны можно также определить:

• как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на ;
• как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
• как пространственный период волнового процесса.

Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву , размерность длины волны — метр ([м]).

Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.

Длина волны — пространственный период волнового процесса[править | править код]

Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний [с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны [м] можно рассматривать как пространственный период волнового процесса. Следует заметить, что круговой частоте колебания [радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» [радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в [м], отличаются ровно на .

Связь с частотой[править | править код]

Получить соотношение, связывающее длину волны с фазовой скоростью и частотой можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому

Для электромагнитных волн в вакууме скорость в этой формуле равна скорости света (299 792 458 м/с), и длина волны
. Если значение подставить в герцах, то  будет выражена в метрах.

Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.

Длина волны в среде[править | править код]

Длина электромагнитной волны в среде короче, чем в вакууме:

где  — показатель преломления среды;

 — относительная диэлектрическая проницаемость среды;

 — относительная магнитная проницаемость среды.

Величины , и могут существенно зависеть от частоты (явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне (для диэлектриков , для ферромагнетиков с ростом частоты ), то в инженерной практике используют величину , которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) = 2,56, и коэффициент укорочения = 1/1,6 = 0,625.

Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением , но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же .

Волны де Бройля[править | править код]

Волнам де Бройля также соответствует определённая длина волны. Частице с энергией и импульсом , соответствуют:

• частота:
• длина волны:

где  — постоянная Планка.

Примеры[править | править код]

Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару ↔ , например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм^[4].

Примечания[править | править код]

Литература[править | править код]

• Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
• Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).