|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам:
Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим
Ксарфакс 4 года назад Периметр по координатам Периметр фигуры – это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2):
Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 – x1)^2 + (y2 – y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:
Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((12 – 1)^2 + ((-5) – 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((-2 – 12)^2 + (1 – -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 – (-2))^2 + (8 – 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты.
Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым – просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула:
, где х1 и х2 – координаты концов отрезка по оси х, а y1 и y2 – координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины.
Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы
Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр.
Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр – сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула:
где точка А имеет координаты (x1; y1), а точка В – координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС.
габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 – x1^2) + (y2^2 – y1^2), х1 и у1 координаты начала, х2,у2 – координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр – это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb – xa)2 + (yb – ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb – xa)2 + (yb – ya)2 + (zb – za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2):
Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить – получить.
Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле:
У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле.
Складываем полученные результаты и получаем периметр.
Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр.
Знаете ответ? |
Загрузить PDF
Загрузить PDF
Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.[1]
С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.
-

1
Запишите формулу для вычисления длины. Формула:
, где
— длина отрезка,
— координаты начальной точки отрезка,
— координаты конечной точки отрезка.[2]
-

2
Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.[3]
-

3
Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты
должны находится внутри первой пары скобок, а две координаты
— внутри второй пары скобок.[4]
Реклама
-

1
Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.[5]
-

2
Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.[6]
-

3
Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.
-

4
Вычислите длину отрезка
. Для этого извлеките корень из полученной суммы чисел.
Реклама
Советы
- Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
- Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.
Реклама
Об этой статье
Эту страницу просматривали 24 315 раз.
Была ли эта статья полезной?
Длина отрезка. Расстояние между точками: онлайн-калькулятор
Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:
- Задать размерность (плоскость или пространство).
- Ввести в поля координаты точек.
- Нажать «рассчитать».
Расстояние между точками онлайн
Для нахождения длины отрезка по координатам существует формула. Для отрезка AB в трехмерном пространстве она имеет вид:
d=xb-xa2+yb-ya2+zb-za2
Даже если вы забыли данную формулу, расстояние между точками всегда можно найти по координатам онлайн. Калькулятор не только предоставляет правильный ответ, но и подробно расписывает решение.
Онлайн-калькулятор нахождения длины отрезка по координатам будет полезен школьникам и студентам в самостоятельной подготовке, а также преподавателям и всем любителям математики.
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Модуль вектора а будем обозначать  .
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор  имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора  , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор
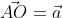 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 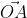 получаем
получаем
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор  дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 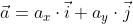 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле  , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор  =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a  )
)
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a  , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор  имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
При этом формула вычисления длины вектора  для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 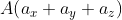 и
и 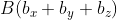 ), будет следующей:
), будет следующей:
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
Геометрия для новичков. Часть 1: координаты и векторы – теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:

На этом рисунке крупные черные точки – это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора

Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx – Ax
y = By – Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это – лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок

Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор

Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это – не вектор.
В нашем примере направленный отрезок  представляет вектор
представляет вектор  . Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например:
. Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например: 
Примечание: о тонкостях приведенного мной определения – в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора  и
и  , представленные направленными отрезками
, представленные направленными отрезками  и
и  называются равными, если:
называются равными, если:
Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы

На рисунке любая пара из векторов  ,
,  ,
,  является коллинеарными векторами
является коллинеарными векторами
Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:

Пишут: 


Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:

Пишут: 


Нулевой вектор
Единичные векторы
 =1
=1
Обратный вектор

Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
 , умноженный на число, записывается как k*
, умноженный на число, записывается как k* . Вектор будет сонаправлен (противоположно направлен) с вектором
. Вектор будет сонаправлен (противоположно направлен) с вектором  , если k – положительное (отрицательное) число. Вектор k*
, если k – положительное (отрицательное) число. Вектор k*  будет иметь длину |k|*|
будет иметь длину |k|*| |:
|:
|k* | = |k|*|
| = |k|*| |
|
k* 

 , если k>0
, если k>0
k* 

 , если k 0, такое, что:
, если k 0, такое, что:
|k *  |=1
|=1
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором 
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k* | = |k|*|
| = |k|*| | = k * 0 = 0
| = k * 0 = 0
Итак, как же найти это число k?
Распишем |k *  | по определению:
| по определению:
|k *  | = |k| * |
| = |k| * | | = k * |
| = k * | | = 1
| = 1
Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * | | = 1
| = 1
Из этого следует, что:
k = 1 / | |
|
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора – разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора  и
и  ,
,
то для каждого вектора  можно подобрать 2 числа k и s, для которых выполняется равенство:
можно подобрать 2 числа k и s, для которых выполняется равенство:
 = k*
= k*  + s*
+ s*
Теперь возьмем в качестве таких неколлинеарных векторов  и
и  следующие векторы:
следующие векторы:
- вектор
 – направление – вдоль оси Ox, длина равна 1
– направление – вдоль оси Ox, длина равна 1 - вектор
 – направление – вдоль оси Oy, длина равна 1
– направление – вдоль оси Oy, длина равна 1

Векторы  и
и  называют координатными векторами.
называют координатными векторами.
Определение координат вектора
 = x*
= x*  + y*
+ y*
то пара чисел (x, y) будет называться координатами вектора  .
.
Часто пишут:
 = (x, y)
= (x, y)
Эта запись означает, что вектор  имеет координаты x и y.
имеет координаты x и y.
Арифметические операции над координатами векторов
–  = (-ax, -ay)
= (-ax, -ay)
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k*  = (k*ax, k*ay)
= (k*ax, k*ay)
Пусть у нас есть 2 произвольных вектора  =(ax, ay) и
=(ax, ay) и  =(bx, by). Тогда:
=(bx, by). Тогда:
- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
 +
+  = (ax + bx, ay + by)
= (ax + bx, ay + by) - как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
 –
–  = (ax – bx, ay – by)
= (ax – bx, ay – by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор

Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт:  =(Ax, Ay)
=(Ax, Ay)
где (Ax, Ay) – координаты точки A
Связь между координатами вектора и координатами концов отрезка
если  – направленный отрезок, представляющий вектор
– направленный отрезок, представляющий вектор  , то значения координат вектора
, то значения координат вектора  (x, y) вычисляются по формуле:
(x, y) вычисляются по формуле:
(x, y) = (Bx – Ax, By – Ay)
где (Ax, Ay), (Bx, By) – координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора  :
:
 =
=  –
– 

Заметим, что  и
и  – радиус векторы.
– радиус векторы.
Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx – Ax, By – Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор  , представленный отрезком
, представленный отрезком  . Координаты вектора
. Координаты вектора  равны (x, y).
равны (x, y).
Чтобы найти длину вектора  через его координаты, воспользуемся теоремой Пифагора и равенством:
через его координаты, воспользуемся теоремой Пифагора и равенством:
 =
=  +
+ 

По теореме Пифагора:

AC = | | = |x|,
| = |x|,
СB = | | = |y|
| = |y|
то в итоге получаем равенство:

Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье “свое” определение вектора.
Координаты вектора как найти длину отрезка по двум точкам, правило и формула нахождения в пространстве, свойства, задачи с решением, онлайн-калькулятор
При рассмотрении отрезков с заданным направлением часто используют декартову систему координат. Найти на ней вектор — значит, определить значения начальной и конечной точки. То есть при решении задач оперируют не геометрическими параметрами, а числовыми характеристиками. Такой подход позволяет перейти от геометрии к алгебре. Этот метод называется координатным и применим как к плоскому пространству — двухмерному, так и объёмному — трёхмерному.

Общие сведения

Под термином «вектор» принято понимать прямую с определённым направлением, ограниченную начальной и конечной точкой. Фактически это отрезок, в котором известно, где его начало и конец. Обозначают его с помощью заглавных латинских букв и стрелочкой над ними. Например, если имеется вектор, берущий начало в точке A и заканчивающийся в B, то его подписывают как AB. Но также существует и короткое обозначение — одной малой буквой со стрелкой (чертой) над ней.
При работе с отрезками приходится сталкиваться с понятием «коллинеарность». Если векторы можно совместить параллельным переносом, и линии необязательно являются равными, то их называют коллинеарными. При этом их направление не имеет значения. Если же они совпадают по нему, то такие отрезки называют сонаправленными.
Тут следует учесть, что отрезки будут направлены в одну сторону лишь только тогда, когда их лучи находятся по одну сторону от прямой, объединяющей их начала. Когда векторы коллинеарны и не сонаправлены, то они противоположные. Осюда можно сформулировать правило, что два ненулевых вектора являются коллинеарными, если они располагаются на одной или на параллельных прямых. Причём точка считается коллинеарной любому отрезку.
При работе с отрезками можно выполнять различные арифметические операции на основании их свойств. Математические правила нахождения положения общего вектора называются линейными. Выделяют следующие действия над ограниченными прямыми:

Кроме того, вектор можно умножить на число или разложить на составляющие компоненты. Всё это позволяет построить базисный отрезок для нахождения в дальнейшем его координат. При этом если существует перпендикулярность двух векторов, то отрезок к направляющей ограниченной линии называют нормальным или ортогональным.
Проекция на ось координат
Определить координаты отрезка возможно различными способами. Один из них — использование проекции. Другими словами, изображаются в координатных плоскостях начало и конец вектора, которые соединяются прямой линией. Откладывать расположение точек нужно в соответствии с используемым масштабом. После с помощью перпендикулярных координатным осям линий на них переносят расположение начала и конца вектора, то есть как бы проецируют отрезок на оси.
При этом если направление перенесённого вектор совпадает с направлением оси, то проекция обозначается со знаком плюс, если же оно противоположное — со знаком минус. Обозначают перенос отрезков символом ПР. Существуют несколько свойств, характерных для проекции:

Если отрезок располагается перпендикулярно оси, то его проекцией будет точка. Для декартовой системы координат в записи вектора на одном из мест будет стоять ноль. Например, AB (0; 1) или AB (-3; 0). Для задания направления в пространстве применяют так называемый единичный вектор.
Другими словами, он является отрезком нормирования пространства и обозначает масштаб проекции. Его выбирают в качестве базисного вектора, что заметно помогает упростить расчёты. Для того чтобы его вычислить, необходимо вектор разделить на длину: e = AB / | AB |. Такая операция называется нормированием.
Формула координат

При построении отрезка единичный вектор выбирается исходя из удобства размещения его в плоскости. Начальная и конечная точка могут быть определены в координатной плоскости. Чаще всего для этого используется декартова система координат. К расположениям осей жёстких требований нет, но принято по горизонтали рисовать ось икс в правом направлении, а по вертикали снизу вверх — ось игрек. Пересекаются эти оси между собой под прямым углом и место их пересечения называют началом отсчёта. В этой точке координата записывается как (0, 0).
Задать координаты, значит, присвоить точке два числа. Так, если точка имеет координаты x = 4; y = -2, то обозначаться она будет как A (4, -2). Ось от нуля в направлении икса называется абсциссой, а совпадающая с игреком — ординатой. В плоскости каждая точка заданного отрезка характеризуются двумя значениями. Одно из них соответствует оси ординат, а другое абсцисс. Например, A (1, 5); B (3, 2). Здесь единица и тройка соответствуют значению точек на оси икс, а пятёрка и двойка — на оси игрек.
Исходя из этого, чтобы нарисовать вектор на плоскости, нужно узнать координаты его начальной и конечной точек, а также направление. Для получения рисунка вектора нужно просто соединить эти две точки. Из знания значений, ограничивающих точки отрезка, довольно легко определить координаты вектора.
Существует простое правило, которое гласит, что для этого необходимо из координат конечной точки вычесть координаты начальной. Для рассмотренного примера с точками A (1, 5); B (3, 2) координаты вектора будут: AB = (2 — 1); (3 — 5). То есть справедливо будет записать: AB (1; -2). Для общего случая можно сказать, что формула координаты вектора по двум точкам имеет следующий вид: AB (x2 — x1, y2 − y1), где икс и игрек один — положение первой точки, а икс и игрек два — второй.
Это выражение справедливо не только для плоскости, но и для нахождения координат в пространстве. В этом случае добавляется третья осью. Обозначается она часто буквой Z. Соответственно, каждая точка будет описываться уже не двумя координатными значениями, а тремя — по числу осей: A (x1, y1, z1) и B (x2, y2, z2). Отсюда следует, что координаты вектора определяются уже по формуле: AB = (x2 — x1; y2 — y1; z2 — z1).
При сложении, умножении, вычитании двух ограниченных линий нужно выполнять поэлементно действия над их координатами. Например, AB (x 1, y 1) + BC (x 2, y 2) = AC (x 1 + x 2, y 1 + y 2).
Примеры решения задач
В своём большинстве задачи на поиск длины вектора по координатам или просто вычисление расположения отрезка в плоскости не представляет труда. Но эти действия нужно уметь выполнять, так как проекции очень часто используются при рассмотрении различных физических процессов.
Есть типовые задачи, дающиеся в седьмом классе средней школы для самостоятельной работы. Проработав их и научившись находить ответ, можно будет утверждать о знании темы. Вот один из вариантов примеров разной сложности:

Вот задача посложнее. Имеются две точки на плоскости. Первая имеет координаты L (1, 5), а вторая J (2, 7). Нужно найти длину соединяющего их отрезка. Для наглядности можно нарисовать чертёж, на которой изобразить эти две точки и объединяющую их прямую. Затем из этих координат нужно провести два перпендикуляра, таким образом, чтобы они пересеклись. Место их пересечения нужно как-то обозначить. Пусть это будет буква T.
Посмотрев на рисунок, можно заметить, что полученная фигура есть не что иное, как прямоугольный треугольник. Получается, что отрезки LT и JT— это катеты. Поэтому нужно лишь найти их длины по модулю и применить теорему Пифагора. Осюда, длина: |LT| = x2 — x1 = 7 — 5 = 2, |JT| = 2 — 1 =1. Исходя из формулы для нахождения гипотенузы, искомая длина будет равняться: d = √ LT 2 + JT 2 = √ 2 2 + 1 2 = √5.
Таким образом, все задачи на нахождение длины или расположения отрезка решаются через формулу координат. При этом не имеет значения, какое пространство рассматривается. Она справедлива как к двухмерному, так и n-мерному.
Использование онлайн-калькулятора

На практике чаще всего решение задач подразумевает нахождение какого-либо параметра в пространстве. Особенно это характерно для физики при изучении электромагнетизма или движения. Нередко приходится на координатных осях откладывать точки, в итоге образующие сложную фигуру. Поэтому даже незначительная, на первый взгляд, ошибка приведёт к неправильному ответу.
Гораздо эффективнее использовать так называемые онлайн-калькуляторы. Это обычные сайты, содержащие специальные программы для расчёта математических заданий. Пользоваться ими сможет любой, у кого есть доступ к интернету и установленный веб-браузер. Всё что требуется от пользователя, это просто в предложенную форму ввести исходные данные и нажать интерактивную кнопку, часто подписанную «Вычислить». Приложение запустится автоматически и через несколько секунд выдаст ответ. При этом за его точность можно не переживать. Ведь в основе работы программы используются алгоритмы на основе математических формул.
Из наиболее популярных сервисов, предоставляющих бесплатный доступ к своим услугам, можно выделить следующие:
- ru.onlinemschool;
- ru.solverbook;
- math.semestr;
- geleot;
- mathonline.um-razum.

Это сервисы доступны на русском языке, имеют простой и понятный интерфейс. Их услуги привлекательны как для инженеров, выполняющим сложные расчёты, так и учащихся. Для первых это экономия времени и точный результат, а для вторых — отличное подспорье в учёбе. Всё дело в том, что эти сайты на своих страницах содержат весь необходимый теоретический материал с примерами вычислений. Кроме того, программа не просто выдаёт расчёт, но и выводит на дисплей пошаговое решение с описанием ключевых моментов.
Таким образом, даже ничего не понимая, ученик, попробовав решить несколько заданий, научится самостоятельно вычислять ответ. Векторные формулы отлично поддаются автоматизированному вычислению. Поэтому часто есть резон решать задания по нахождению векторных координат на онлайн-калькуляторе.
[spoiler title=”источники:”]
http://gamedev.ru/code/articles/geometry_for_beginners_1
http://sprint-olympic.ru/uroki/algebra/78091-koordinaty-vektora-kak-naiti-dliny-otrezka-po-dvym-tochkam-pravilo-i-formyla-nahojdeniia-v-prostranstve-svoistva-zadachi-s-resheniem-onlain-kalkyliator.html
[/spoiler]
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
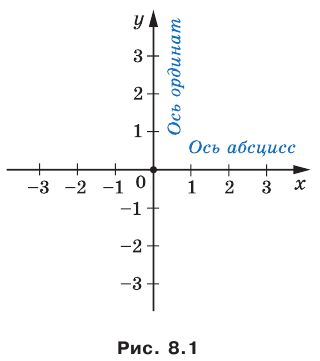
Договорились координатную плоскость с осью 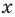
Координаты точки на плоскости 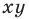 называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
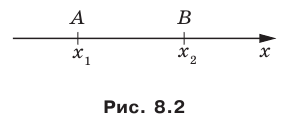
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 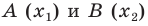 (рис. 8.2) имеем:
(рис. 8.2) имеем:
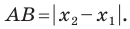
Научимся находить расстояние между точками 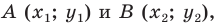 заданными на плоскости
заданными на плоскости 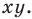
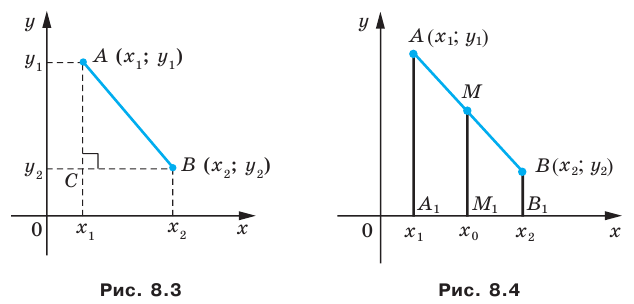
Рассмотрим случай, когда отрезок 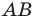 не перпендикулярен ни одной из координатных осей (рис. 8.3).
не перпендикулярен ни одной из координатных осей (рис. 8.3).
Через точки 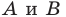 проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник
проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник 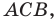 в котором
в котором 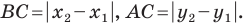 Отсюда
Отсюда 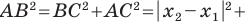
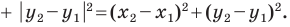
Тогда формулу расстояния между точками 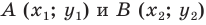 можно записать так:
можно записать так:

Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 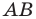 перпендикулярен одной из осей координат.
перпендикулярен одной из осей координат.
Пусть 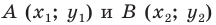 — точки плоскости
— точки плоскости 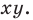 Найдем координаты
Найдем координаты 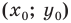 точки
точки 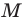 — середины отрезка
— середины отрезка 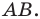
Рассмотрим случай, когда отрезок 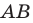 не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что
не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что 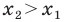 (случай, когда
(случай, когда 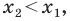 рассматривается аналогично). Через точки
рассматривается аналогично). Через точки 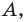
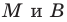 проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках
проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках 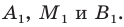 По теореме Фалеса
По теореме Фалеса 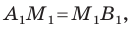 тогда
тогда 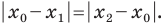 Поскольку
Поскольку 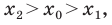 то можем записать:
то можем записать: 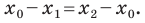 Отсюда
Отсюда  Аналогично можно показать что
Аналогично можно показать что 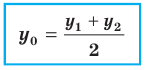
Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 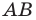 перпендикулярен одной из осей координат. Докажите это самостоятельно.
перпендикулярен одной из осей координат. Докажите это самостоятельно.
Пример №1
Докажите, что треугольник с вершинами в точках 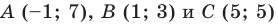 является равнобедренным прямоугольным.
является равнобедренным прямоугольным.
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
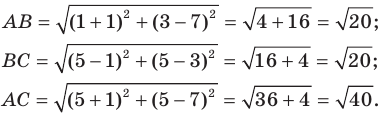
Следовательно, 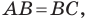 то есть треугольник
то есть треугольник 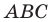 равнобедренный.
равнобедренный.
Поскольку 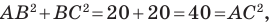 то треугольник
то треугольник 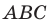 прямоугольный.
прямоугольный. 
Пример №2
Точка 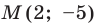 — середина отрезка
— середина отрезка 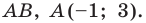 Найдите координаты точки
Найдите координаты точки 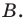
Решение:
Обозначим 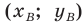 — координаты точки
— координаты точки 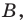
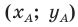 — координаты точки
— координаты точки 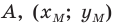 — координаты точки
— координаты точки 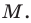
Поскольку 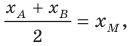 то получаем:
то получаем: 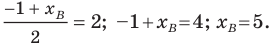
Аналогично 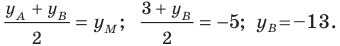
Ответ: 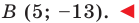
Пример №3
Докажите, что четырехугольник 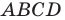 с вершинами в точках
с вершинами в точках 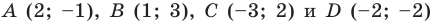 является прямоугольником.
является прямоугольником.
Решение:
Пусть точка 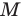 — середина диагонали
— середина диагонали 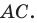 Тогда
Тогда
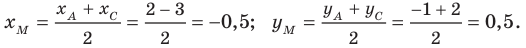
Следовательно, 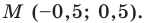
Пусть точка 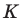 — середина диагонали
— середина диагонали 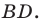 Тогда
Тогда
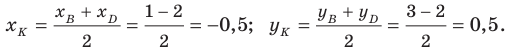
Следовательно, 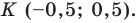
Таким образом, точки 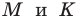 совпадают, то есть диагонали четырехугольника
совпадают, то есть диагонали четырехугольника  имеют общую середину. Отсюда следует, что четырехугольник
имеют общую середину. Отсюда следует, что четырехугольник  — параллелограмм.
— параллелограмм.
Найдем диагонали параллелограмма:
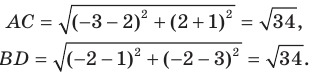
Следовательно, диагонали параллелограмма  равны. Отсюда следует, что этот параллелограмм является прямоугольником.
равны. Отсюда следует, что этот параллелограмм является прямоугольником. 
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
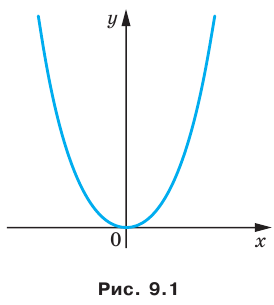
Координаты 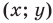 каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения
каждой точки параболы, изображенной на рисунке 9.1, являются решением уравнения 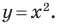 И наоборот, каждое решение уравнения с двумя переменными
И наоборот, каждое решение уравнения с двумя переменными 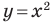 является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид
является координатами точки, лежащей на этой параболе. В этом случае говорят, что уравнение параболы, изображенной на рисунке 9.1, имеет вид 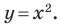
Определение. Уравнением фигуры  заданной на плоскости
заданной на плоскости 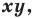 называют уравнение с двумя переменными
называют уравнение с двумя переменными 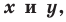 обладающее следующими свойствами:
обладающее следующими свойствами:
- если точка принадлежит фигуре
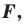 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения; - любое решение
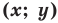 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 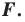
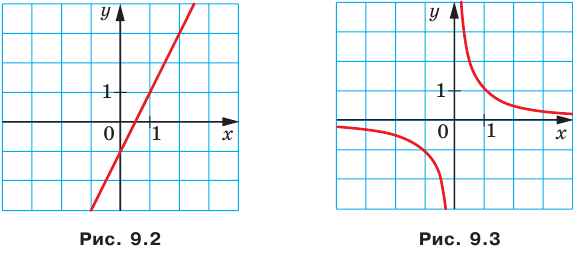
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 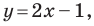 а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид
а уравнение гиперболы, изображенной на рисунке 9.3, имеет вид 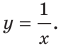 Принято говорить, что, например, уравнения
Принято говорить, что, например, уравнения 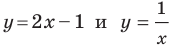 задают прямую и гиперболу соответственно.
задают прямую и гиперболу соответственно.
Если данное уравнение является уравнением фигуры 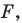 то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
то эту фигуру можно рассматривать как геометрическое место точек (ГМТ), координаты которых удовлетворяют данному уравнению.
Пользуясь этими соображениями, выведем уравнение окружности радиуса 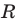 с центром в точке
с центром в точке 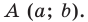
Пусть 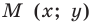 — произвольная точка данной окружности (рис. 9.4). Тогда
— произвольная точка данной окружности (рис. 9.4). Тогда 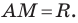 Используя формулу расстояния между точками, получим:
Используя формулу расстояния между точками, получим:
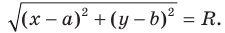
Отсюда
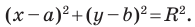
Мы показали, что координаты 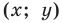 произвольной точки
произвольной точки 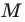 данной окружности являются решением уравнения
данной окружности являются решением уравнения 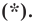 Теперь покажем, что любое решение уравнения
Теперь покажем, что любое решение уравнения 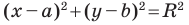 является координатами точки, принадлежащей данной окружности.
является координатами точки, принадлежащей данной окружности.
Пусть пара чисел 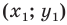 — произвольное решение уравнения
— произвольное решение уравнения 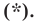
Тогда 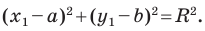 Отсюда
Отсюда 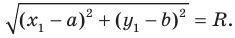
Это равенство показывает, что точка 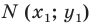 удалена от центра окружности
удалена от центра окружности 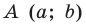 на расстояние, равное радиусу окружности, а следовательно, точка
на расстояние, равное радиусу окружности, а следовательно, точка 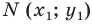 принадлежит данной окружности.
принадлежит данной окружности.
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 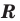 с центром в точке
с центром в точке 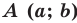 имеет вид
имеет вид
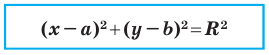
Верно и такое утверждение: любое уравнение вида 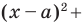 где
где 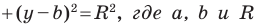 некоторые числа, причем
некоторые числа, причем 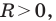 является уравнением окружности радиуса
является уравнением окружности радиуса 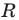 с центром в точке с координатами
с центром в точке с координатами 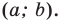
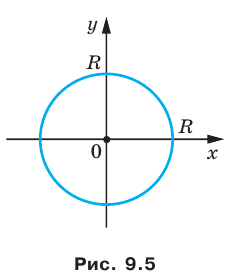
Если центром окружности является начало координат (рис. 9.5), то 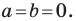 В этом случае уравнение окружности имеет вид
В этом случае уравнение окружности имеет вид 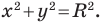
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 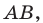 если
если 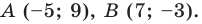
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 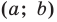 центра
центра 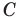 окружности:
окружности:
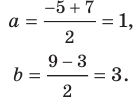
Следовательно, 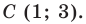
Радиус окружности 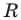 равен отрезку
равен отрезку 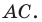 Тогда
Тогда
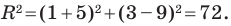
Следовательно, искомое уравнение имеет вид
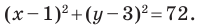
Ответ: 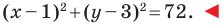
Пример №5
Докажите, что уравнение 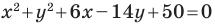 задает окружность. Найдите координаты центра и радиус этой окружности.
задает окружность. Найдите координаты центра и радиус этой окружности.
Решение:
Представим данное уравнение в виде 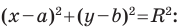
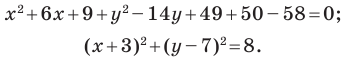
Следовательно, данное уравнение является уравнением окружности с центром в точке 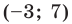 и радиусом
и радиусом 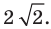
Ответ: 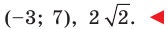
Пример №6
Докажите, что треугольник с вершинами в точках 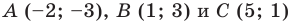 является прямоугольным, и составьте уравнение окружности, описанной около треугольника
является прямоугольным, и составьте уравнение окружности, описанной около треугольника 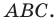
Решение:
Найдем квадраты сторон данного треугольника:
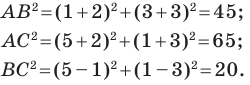
Поскольку 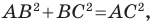 то данный треугольник является прямоугольным с прямым углом при вершине
то данный треугольник является прямоугольным с прямым углом при вершине 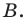 Центром описанной окружности является середина гипотенузы
Центром описанной окружности является середина гипотенузы 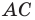 — точка
— точка 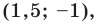 радиус окружности
радиус окружности 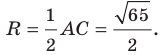 Следовательно, искомое уравнение имеет вид
Следовательно, искомое уравнение имеет вид
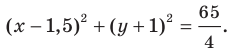
Ответ: 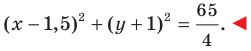
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
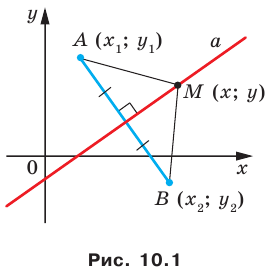
Пусть 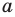 — данная прямая. Выберем две точки
— данная прямая. Выберем две точки 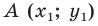 и
и 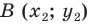 так, чтобы прямая
так, чтобы прямая 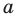 была серединным перпендикуляром отрезка
была серединным перпендикуляром отрезка 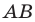 (рис. 10.1).
(рис. 10.1).
Пусть 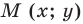 — произвольная точка прямой
— произвольная точка прямой 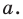 Тогда по свойству серединного перпендикуляра отрезка выполняется равенство
Тогда по свойству серединного перпендикуляра отрезка выполняется равенство 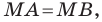 то есть
то есть
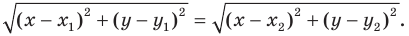
Мы показали, что координаты 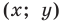 произвольной точки
произвольной точки 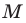 прямой
прямой 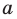 являются решением уравнения
являются решением уравнения 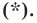
Теперь покажем, что любое решение уравнения  является координатами точки, принадлежащей данной прямой
является координатами точки, принадлежащей данной прямой 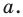
Пусть 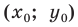 — произвольное решение уравнения
— произвольное решение уравнения 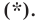 Тогда
Тогда 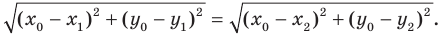 Это равенство означает, что точка
Это равенство означает, что точка 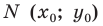 равноудалена от точек
равноудалена от точек 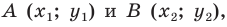 следовательно, точка
следовательно, точка 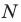 принадлежит серединному перпендикуляру отрезка
принадлежит серединному перпендикуляру отрезка 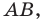 то есть прямой
то есть прямой 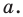
Итак, мы доказали, что уравнение 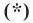 является уравнением данной прямой
является уравнением данной прямой 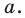
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 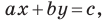 где
где 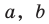 и
и 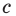 — некоторые числа, причем
— некоторые числа, причем 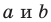 не равны нулю одновременно. Покажем, что уравнение
не равны нулю одновременно. Покажем, что уравнение 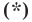 можно преобразовать к такому виду. Возведем обе части уравнения
можно преобразовать к такому виду. Возведем обе части уравнения 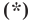 в квадрат. Имеем:
в квадрат. Имеем:
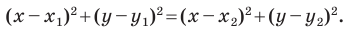
Раскроем скобки и приведем подобные слагаемые. Получим:
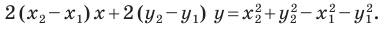
Обозначив 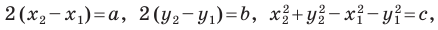 получим уравнение
получим уравнение 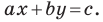
Поскольку точки 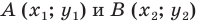 различны, то хотя бы одна из разностей
различны, то хотя бы одна из разностей 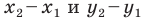 не равна нулю. Следовательно, числа
не равна нулю. Следовательно, числа 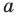 и
и 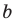 не равны нулю одновременно.
не равны нулю одновременно.
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
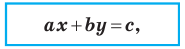
где 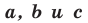 — некоторые числа, причем
— некоторые числа, причем 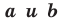 не равны нулю одновременно.
не равны нулю одновременно.
Верно и такое утверждение: любое уравнение вида 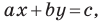 где
где 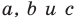 — некоторые числа, причем
— некоторые числа, причем 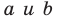 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 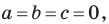 то графиком уравнения
то графиком уравнения 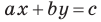 является вся плоскость
является вся плоскость 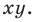 Если
Если 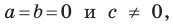 то уравнение не имеет решений.
то уравнение не имеет решений.
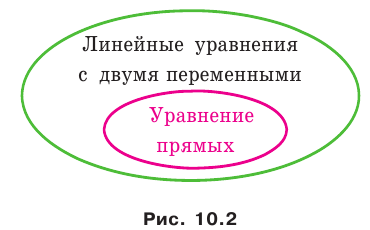
Из курса алгебры 7 класса вы знаете, что уравнение вида 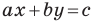 называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 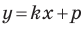 является прямая. Сейчас мы можем это доказать.
является прямая. Сейчас мы можем это доказать.
Перепишем уравнение 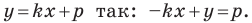 Мы получили уравнение вида
Мы получили уравнение вида 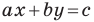 для случая, когда
для случая, когда 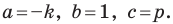 Поскольку в этом уравнении
Поскольку в этом уравнении 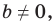 то мы получили уравнение прямой.
то мы получили уравнение прямой.
А любую ли прямую на плоскости можно задать уравнением вида 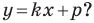 Ответ на этот вопрос отрицательный.
Ответ на этот вопрос отрицательный.
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида 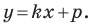
Вместе с тем, если в уравнении прямой 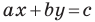 принять
принять 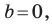 то его можно переписать так:
то его можно переписать так: 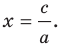 Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Если 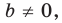 то уравнение прямой
то уравнение прямой 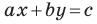 можно записать так:
можно записать так:
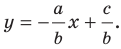 Обозначив
Обозначив 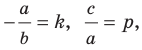 получим уравнение
получим уравнение 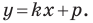
Следовательно, если 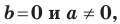 то уравнение прямой
то уравнение прямой 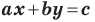 задает вертикальную прямую; если
задает вертикальную прямую; если 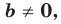 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Уравнение невертикальной прямой удобно записывать в виде 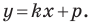
Данная таблица подытоживает материал, рассмотренный в этом пункте.

Пример №7
Составьте уравнение прямой, проходящей через точки:

Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 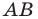 является вертикальной. Ее уравнение имеет вид
является вертикальной. Ее уравнение имеет вид 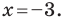
2) Поскольку данные точки имеют разные абсциссы, то прямая 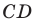 не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде
не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде 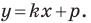
Подставив координаты точек 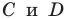 в уравнение
в уравнение 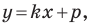 получаем систему уравнений:
получаем систему уравнений:
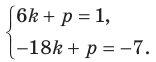
Решив эту систему уравнений, находим, что 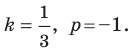
Ответ: 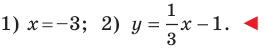
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 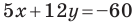 и осями координат.
и осями координат.
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 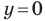 получаем
получаем 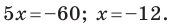
С осью ординат: при 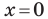 получаем
получаем 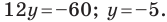
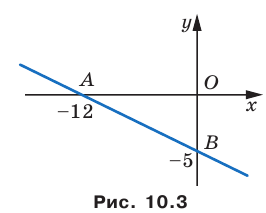
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 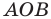 (рис. 10.3) с вершинами
(рис. 10.3) с вершинами 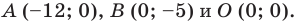 Найдем стороны треугольника:
Найдем стороны треугольника: 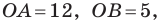
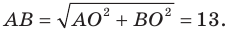 Тогда искомые периметр и площадь соответственно равны
Тогда искомые периметр и площадь соответственно равны 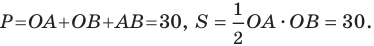
Ответ: 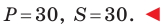
Угловой коэффициент прямой
Рассмотрим уравнение 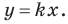 Оно задает невертикальную прямую, проходящую через начало координат.
Оно задает невертикальную прямую, проходящую через начало координат.
Покажем, что прямые 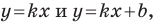 где
где 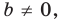 параллельны.
параллельны.
Точки 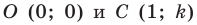 принадлежат прямой
принадлежат прямой 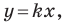 а точки
а точки 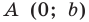 и
и 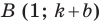 принадлежат прямой
принадлежат прямой 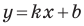 (рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей
(рис. 11.1). Легко убедиться (сделайте это самостоятельно), что середины диагоналей 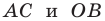 четырехугольника
четырехугольника 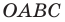 совпадают. Следовательно, четырехугольник
совпадают. Следовательно, четырехугольник 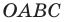 — параллелограмм. Отсюда
— параллелограмм. Отсюда 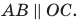
Теперь мы можем сделать такой вывод: если 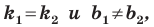 то прямые
то прямые 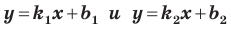 параллельны (1).
параллельны (1).
Пусть прямая 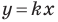 пересекает единичную полуокружность в точке
пересекает единичную полуокружность в точке 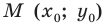 (рис. 11.2). Угол
(рис. 11.2). Угол 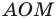 называют углом между данной прямой и положительным направлением оси абсцисс.
называют углом между данной прямой и положительным направлением оси абсцисс.
Если прямая 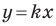 совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным
совпадает с осью абсцисс, то угол между этой прямой и положительным направлением оси абсцисс считают равным 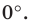
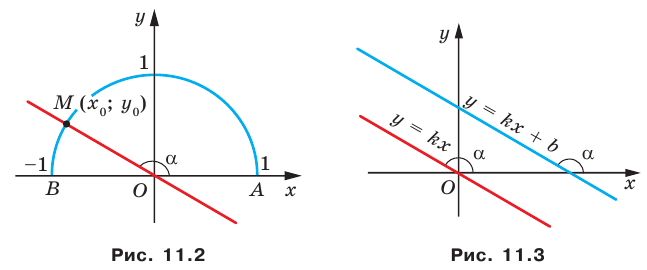 Если прямая
Если прямая 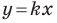 образует с положительным направлением оси абсцисс угол
образует с положительным направлением оси абсцисс угол 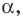 то считают, что и прямая
то считают, что и прямая 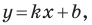 параллельная прямой
параллельная прямой 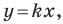 также образует угол
также образует угол 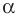 с положительным направлением оси абсцисс (рис. 11.3).
с положительным направлением оси абсцисс (рис. 11.3).
Рассмотрим прямую 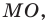 уравнение которой имеет вид
уравнение которой имеет вид 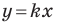 (рис. 11.2). Если
(рис. 11.2). Если 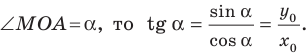 Поскольку точка
Поскольку точка 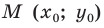 принадлежит прямой
принадлежит прямой 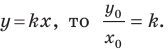 Отсюда
Отсюда 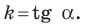 Таким образом, для прямой
Таким образом, для прямой 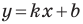 получаем, что
получаем, что
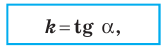
где 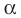 — угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент
— угол, который образует эта прямая с положительным направлением оси абсцисс. Поэтому коэффициент 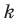 называют угловым коэффициентом этой прямой.
называют угловым коэффициентом этой прямой.
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 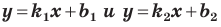 параллельны, то
параллельны, то 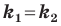 (2).
(2).
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 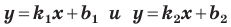 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 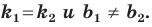
Пример №9
Составьте уравнение прямой, которая проходит через точку 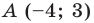 и параллельна прямой
и параллельна прямой 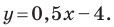
Решение:
Пусть уравнение искомой прямой 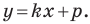 Поскольку эта прямая и прямая
Поскольку эта прямая и прямая 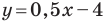 параллельны, то их угловые коэффициенты равны, то есть
параллельны, то их угловые коэффициенты равны, то есть 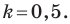
Следовательно, искомое уравнение имеет вид 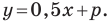 Учитывая, что данная прямая проходит через точку
Учитывая, что данная прямая проходит через точку 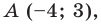 получаем:
получаем: 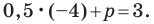 Отсюда
Отсюда 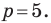
Искомое уравнение имеет вид 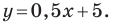
Ответ: 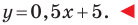
Метод координат
Мы часто говорим: прямая 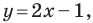 парабола
парабола 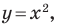 окружность
окружность 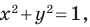 тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
тем самым отождествляя фигуру с ее уравнением. Такой подход позволяет сводить задачу о поиске свойств фигуры к задаче об исследовании ее уравнения. В этом и состоит суть метода координат.
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
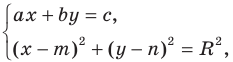
где числа 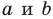 одновременно не равны нулю и
одновременно не равны нулю и 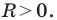
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 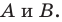 Вы хорошо знаете, какой фигурой является геометрическое место точек
Вы хорошо знаете, какой фигурой является геометрическое место точек 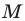 таких, что
таких, что 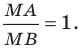
Это серединный перпендикуляр отрезка 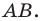 Интересно выяснить, какую фигуру образуют все точки
Интересно выяснить, какую фигуру образуют все точки 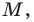 для которых
для которых 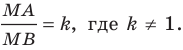 Решим эту задачу для
Решим эту задачу для 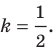
Плоскость, на которой отмечены точки 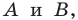 «превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку
«превратим» в координатную. Сделаем это так: в качестве начала координат выберем точку 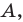 в качестве единичного отрезка — отрезок
в качестве единичного отрезка — отрезок 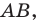 ось абсцисс проведем так, чтобы точка
ось абсцисс проведем так, чтобы точка 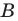 имела координаты
имела координаты 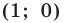 (рис. 11.6).
(рис. 11.6).
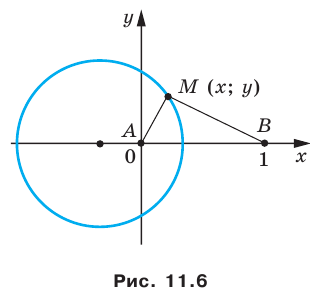
Пусть 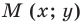 — произвольная точка искомой фигуры
— произвольная точка искомой фигуры 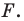 Тогда
Тогда 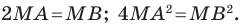 Отсюда
Отсюда
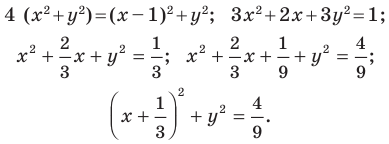
Следовательно, если точка 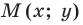 принадлежит фигуре
принадлежит фигуре 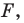 то ее координаты являются решением уравнения
то ее координаты являются решением уравнения 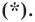
Пусть 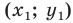 — некоторое решение уравнения
— некоторое решение уравнения 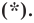 Тогда легко показать, что
Тогда легко показать, что 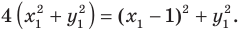 А это означает, что точка
А это означает, что точка 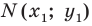 такова, что
такова, что 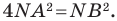 Тогда
Тогда 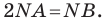 Следовательно, точка
Следовательно, точка 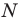 принадлежит фигуре
принадлежит фигуре 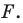
Таким образом, уравнением фигуры 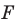 является уравнение
является уравнение 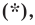 то есть фигура
то есть фигура 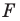 — это окружность с центром в точке
— это окружность с центром в точке 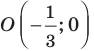 и радиусом
и радиусом 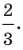
Мы решили задачу для частного случая, когда 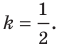 Можно показать, что искомой фигурой для любого положительного
Можно показать, что искомой фигурой для любого положительного 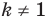 будет окружность. Эту окружность называют окружностью Аполлония
будет окружность. Эту окружность называют окружностью Аполлония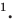
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 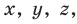 а коэффициенты — первыми:
а коэффициенты — первыми: 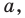
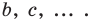 Привычные нам обозначения степеней
Привычные нам обозначения степеней 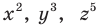 и т. д. также ввел Р. Декарт.
и т. д. также ввел Р. Декарт.

Справочный материал
Расстояние между двумя точками
Расстояние между точками 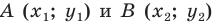 можно найти по формуле
можно найти по формуле 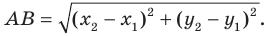
Координаты середины отрезка
Координаты 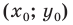 середины отрезка с концами
середины отрезка с концами 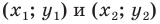 можно найти по формулам:
можно найти по формулам:
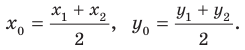
Уравнение фигуры
Уравнением фигуры 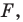 заданной на плоскости
заданной на плоскости 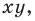 называют уравнение с двумя переменными
называют уравнение с двумя переменными 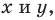 обладающее следующими свойствами:
обладающее следующими свойствами:
1) если точка принадлежит фигуре 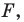 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;
2) любое решение 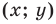 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре 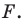
Уравнение окружности
Уравнение окружности радиуса 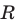 с центром в точке
с центром в точке 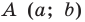 имеет вид
имеет вид 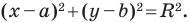
Любое уравнение вида 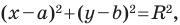 где
где 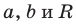 — некоторые числа, причем
— некоторые числа, причем 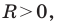 является уравнением окружности радиуса
является уравнением окружности радиуса 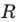 с центром в точке с координатами
с центром в точке с координатами 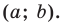
Уравнение прямой
Уравнение прямой имеет вид 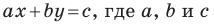 — некоторые числа, причем
— некоторые числа, причем 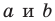 не равны нулю одновременно. Любое уравнение вида
не равны нулю одновременно. Любое уравнение вида 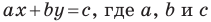 — некоторые числа, причем
— некоторые числа, причем 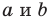 не равны нулю одновременно, является уравнением прямой.
не равны нулю одновременно, является уравнением прямой.
Если 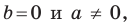 то уравнение прямой
то уравнение прямой 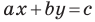 задает вертикальную прямую; если
задает вертикальную прямую; если 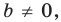 то это уравнение задает невертикальную прямую.
то это уравнение задает невертикальную прямую.
Угловой коэффициент прямой
Коэффициент 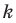 в уравнении прямой
в уравнении прямой 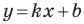 называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
называют угловым коэффициентом прямой, и он равен тангенсу угла, который образует эта прямая с положительным направлением оси абсцисс.
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 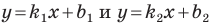 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 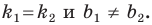
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование













