Как находить длину
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.

Инструкция
Если вам нужно найти длину стороны квадрата, то это не составит труда, если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют одинаковую длину, вычислить величину одной из них можно по формуле: a = √S.
В случае, когда требуется просчитать длину стороны прямоугольника, воспользуйтесь значениями его площади s и длины другой стороны b. Из формулы a=S/b вы получите искомое значение.
Чтобы определить длину окружности, то есть замкнутой линии, которая образует круг, воспользуйтесь значениями: r – ее радиусом и D – диаметром. Диаметр можно вычислить, умножив радиус окружности на 2. Известные вам значения подставьте в формулу определения длины окружности: C=2πr=πD, где π=3,14.
Для вычисления длины обычного отрезка воспользуйтесь методом эксперимента. То есть возьмите линейку и измеряйте.
Для того чтобы вычислить длину стороны такой фигуры, как треугольник, вам понадобятся размеры двух других сторон, а также величины углов. Если вы имеете дело с прямоугольным треугольником, и один из его углов равен 60 градусам, то величину его катета можно определить по формуле a=c*cosα, где c – гипотенуза треугольника, а α – угол между гипотенузой и катетом.
Помимо этого, если вы располагаете такими известными величинами, как высота b и площадь S треугольника, то длину стороны, которая является основанием, можно узнать благодаря формуле a=2√S/√√b.
Что касается правильного многоугольника, то длину его стороны можно просчитать, руководствуясь формулой an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности, n – количество углов.
Если вы хотите вычислить длину равносторонней фигуры, вокруг которой описана окружность, то сделать это можно по формуле an=R√3, где R – радиус окружности, n – количество углов фигуры.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Длина прямоугольника


4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.

Опыт работы учителем математики – более 33 лет.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
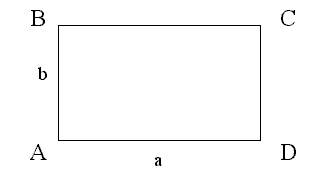
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Значит: d2=a2+b2 . Из этого выражения выразим квадрат ширины (значение «b»):b2=d2-a2
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
-
Через площадь
Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.
-
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c
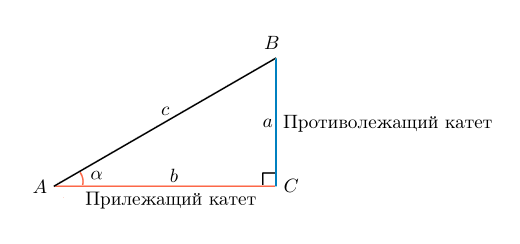
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c
Задача
- Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Корень квадратный из 16 равен 4.
Значение b=4

Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 89.
А какая ваша оценка?
Лучший ответ
$-Z@i4eNOkk-$
Знаток
(461)
12 лет назад
Р=2(а+б) получается периметр поделить на дваи отнять ширину)
Остальные ответы
cHin-cHillo
Гений
(85865)
12 лет назад
ну формула.
периметр = 2*(длина+ширина)
две составляющие известны, находишь длину.
длина = периметр/2-ширина
юю юю
Мыслитель
(6346)
12 лет назад
b=P/2-а
Мария
Знаток
(350)
12 лет назад
Периметр разделить на 2 и отнять ширину
ВЕКтор
Мыслитель
(6359)
12 лет назад
Периметр отнять две ширины и поделить на два.
Ольга Федосеева
Ученик
(191)
7 лет назад
Ширина прямоугольника5мм, периметр4см2ммнайти длину прямоугоьника?
Татка Медведева
Знаток
(259)
7 лет назад
периметр :на 2 – ширина)
Эмиль Гахраманов
Ученик
(123)
7 лет назад
b=P/2-a
Бомбавёнок
Знаток
(260)
7 лет назад
я не то
Радомир Шагабутдинов
Знаток
(285)
7 лет назад
B=Р разделить на 2 и минус A
Иван Липин
Ученик
(128)
6 лет назад
b=P/2-a
Елена Плотникова
Знаток
(319)
6 лет назад
а че писать
pjotr fedorovits
Ученик
(194)
6 лет назад
Как найти длинну прямоугольника если периметр 20 известен, а ширина 3см.?
юрий стал-оол
Ученик
(147)
6 лет назад
Чтобы найти длину Сергей Давыдов. Нужно P поделить на два и отнять ширину.
Формула P 2-b
Евгений Новиков
Ученик
(129)
5 лет назад
Спасибо
Sofia Foxinka
Ученик
(104)
5 лет назад
A= P:2-B
Bayok
Ученик
(202)
4 года назад
,Хер знает
Софья Новикова
Ученик
(109)
2 года назад
а=Р*2-б
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.

Содержание
- Что такое длина прямоугольника
- Три способа найти длину прямоугольника
- Через теорему Пифагора
- Через площадь
- Тригонометрическая функция
- Задача
- Что мы узнали?
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длинна. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.

Рис. 1. Изображение прямоугольника
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известна длина диагонали ( обозначим ее буквой d) и ширина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и ширины будет равен длине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Значит: d2=a2+b2 . Из этого выражения выразим квадрат длины (значение «b»):b2=d2-a2
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула ширины.
-
Через площадь
Рассмотрим еще один способ найти длину прямоугольника. Через площадь.Площадь прямоугольника равняется произведению длины на ширину. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение длины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для ширины: a=S/b.
-
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длинной и диагональю. Обозначим его α. Тогда sin α катета, противоположного углу α к гипотенузе: Sin α = a/d

Рис. 2. Угол альфа на половине прямоугольника
Значение синуса любого угла можно найти в таблицах Брадиса. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а значит воспользуемся основным тригонометрическим тождеством.Косинус это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/d
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*d
Задача
- Найти длину прямоугольника, если известно, что его ширина равна 3, а диагональ 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Корень квадратный из 16 равен 4.
Значение b=4

Рис. 3. Решение задачи
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Предыдущая
МатематикаДиагональ треугольника – формула
Следующая
МатематикаИзмерение углов транспортиром в докладе (5 класс, математика)
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Определение
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать  .
.
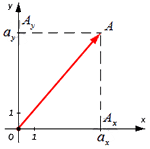
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор  имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора  , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор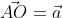 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
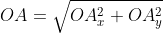
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 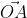 получаем
получаем
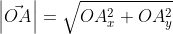
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор  дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 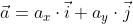 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле  , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Пример
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Необходимо:
Чтобы найти модуль вектора используем ранее приведённую формулу

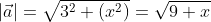
Ответ: 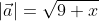
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор  =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a )
)
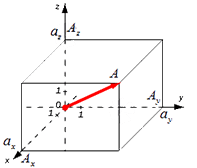
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому
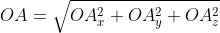
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
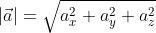
Пример
Необходимо узнать длину вектора ( left|vec{a}right|=2*vec{i}+3*vec{j}+4*vec{k} ), в котором ( vec{i}, vec{j}, vec{k} ), орты.
Решение
Получается, что дан вектор ( left|vec{a}right| ) с координатами (2; 3; 4)
Применив выведенную ранее формулу получим
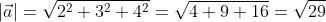
Ответ: 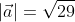
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор  имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
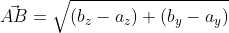
При этом формула вычисления длины вектора  для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 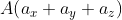 и
и 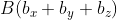 ), будет следующей:
), будет следующей:
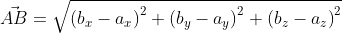
Пример
Для прямой системы координат, найти длину вектора ( overrightarrow{AB}) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
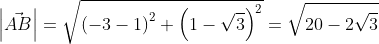
Существует второй вариант решения, где формулы применяются по очереди:
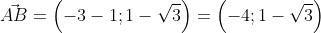
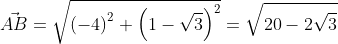
Ответ: 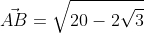
Пример
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
Решение
В первую очередь представим длину вектора в виде формулы.
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
(=sqrt{left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2} = sqrt{26 + left ( lambda^2 -2right )^2})
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
(
sqrt{26+left(lambda^2-2right)^2}=sqrt{30}
)
(
26+left(lambda^2-2right)^2=30
)
(
left(lambda^2-2right)^2=4
)
(
lambda^2-2=2
)
или
(
lambda^2-2=-2
)
(
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Ответ: (
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow{AB}) и (overrightarrow{AC}) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow{BC} ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Пример
Даны длины двух векторов ( overrightarrow{AK}) и ( overrightarrow{AM}) 2 и 4 соответственно, а угол между ними равен ( frac{pi}{3} ) . необходимо найти длину ( overrightarrow{KM}).
Решение
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
(
KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac{pi}{3})
(=2^2+4^2-2cdot2cdot4cdotcosfrac{pi}{3})
(=4+16-16cosfrac{pi}{3})
(=20-8=12
)
Получается (KM=sqrt{12}
)
Ответ: (
left|overrightarrow{KM}right|=sqrt{12}
)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
Первая формула это ( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2}. ), для плоскости
( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2+a_z^2} )
длина вектора формула для трёхмерного пространства;
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vec{AB}right|=sqrt{left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2}) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vec{S}right|=sqrt{ s_x^2+s_y^2}) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
