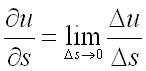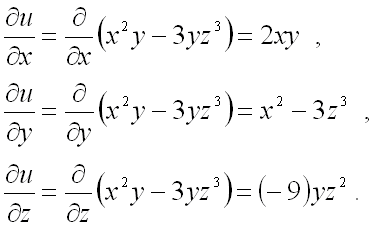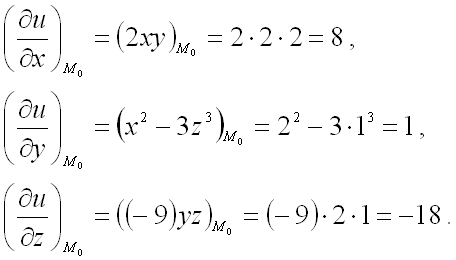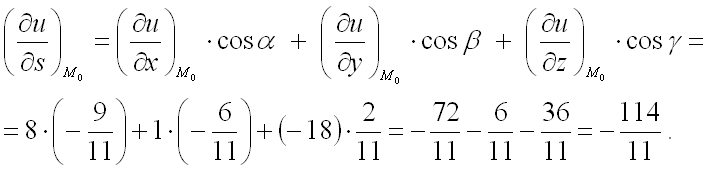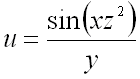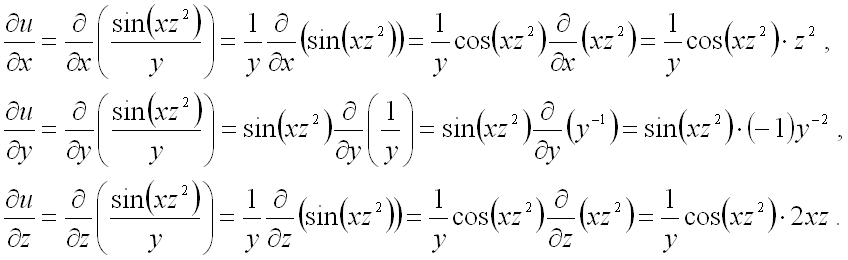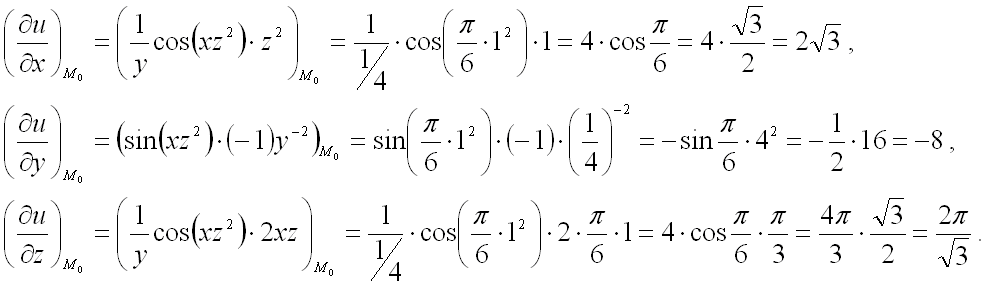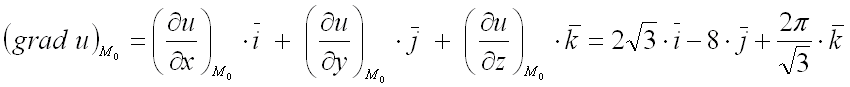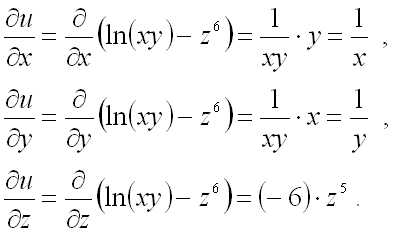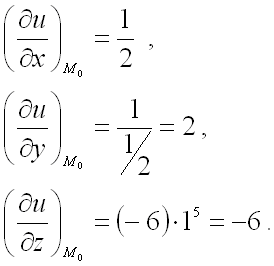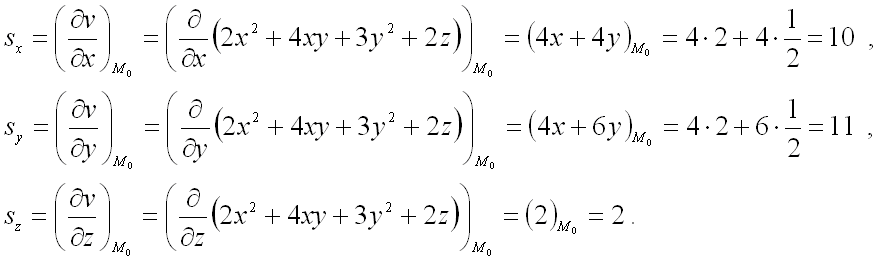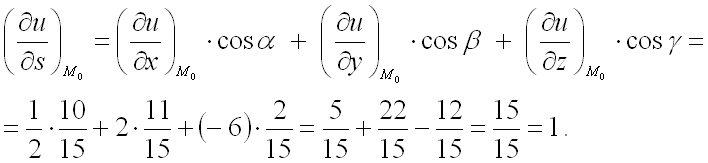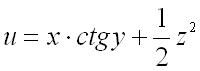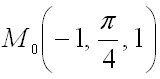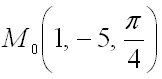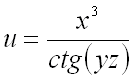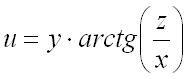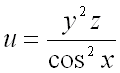Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.
Определение слова “градиент” в математике нужно усвоить.
Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.
Запишем формулу для нахождения вектора градиента:
При нашем раскладе можно с теорией закончить, этого будет достаточно.
Разберём простенький примерчик для начала.
Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.
Было слишком уж просто для нас, возьмём что-нибудь посложнее.
Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.
Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.
Берёмся за дело.
Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.
Другие темы:
Ответы Mail.ru
Наука, Техника, Языки
Гуманитарные науки
Естественные науки
Лингвистика
Техника
Вопросы – лидеры.
Где у скамьи право,а где лево? Я знаю,какие руки у меня))) Вопрос в другом…
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Длина вектора градиента функции
Негр Ганджубасович
Мыслитель
(7988),
закрыт
7 лет назад

Дополнен 7 лет назад
в точке A(-1;2) равна:
а) 7√2
б) 8√2
в) 5√2
г) 9√2
Лучший ответ
Андрей Степанов
Просветленный
(22749)
7 лет назад
grad(z) = i*(y^3 + 8xy) + j*(3xy^2 + 4x^2)
Подставим А (-1; 2)
grad(z) = -8i – 8j
|grad(z)| = sqrt(64 + 64) = sqrt(2*64) = 8*sqrt(2)
Остальные ответы
Рустам Искендеров
Искусственный Интеллект
(133392)
7 лет назад
б).
Похожие вопросы
Производная
по направлению. Градиент
Пусть в некоторой области
задана функция
и точка .
Проведем из точки
вектор ,
направляющие косинусы которого .
На векторе ,
на расстоянии
от его начала рассмотрим точку ,
т.е. 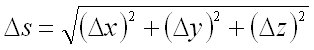
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется
производной от функции
в точке по
направлению вектора
и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: 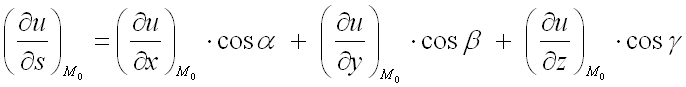
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
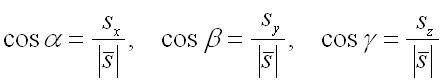
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
и обозначается
или
(читается «набла у»): 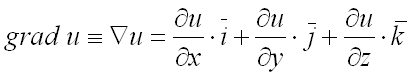
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
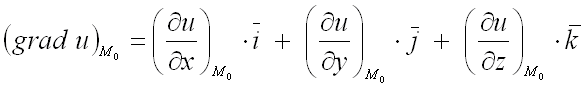
Свойства
градиента
1. Производная
в данной точке по направлению вектора
имеет наибольшее значение, если направление вектора
совпадает с направлением градиента. Это наибольшее значение производной равно
.
2. Производная
по направлению вектора, перпендикулярного к вектору ,
равна нулю.
Примеры
решения задач
Пример 1.
Найти производную от функции
в точке
по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
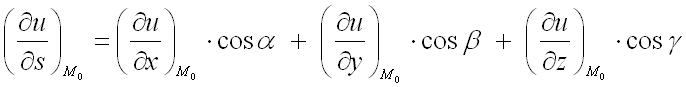
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
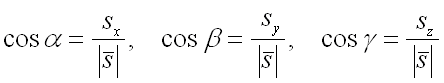
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
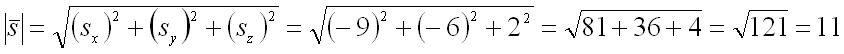
Следовательно, для направляющих косинусов вектора получим следующие значения:
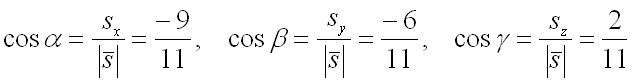
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна 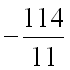
Пример 2.
Найти градиент функции
в точке 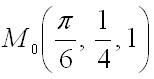
Решение.
Поскольку градиентом функции
называется вектор, проекциями которого на оси координат являются значения частных
производных этой функции в соответствующей точке, то для решения задачи сначала
найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке 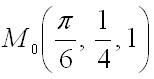
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен 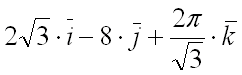
Пример 3.
Найти производную функции
в точке
по направлению градиента функции
в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
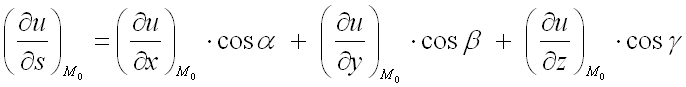
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
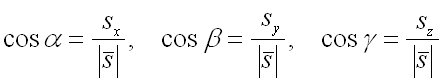
В данном случае вектор совпадает
с градиентом функции
в точке 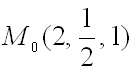
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: 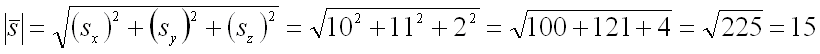
Найдем направляющие косинусы вектор по формулам:
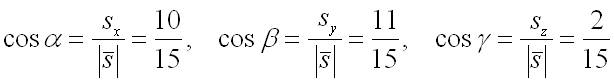
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке 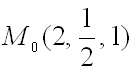
направлению градиента функции
в той же точке равна 1.
Задания
для самостоятельной работы
1.
Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке 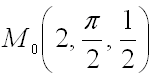
Ответ: .
5. Найти градиент функции
в точке .
Ответ: 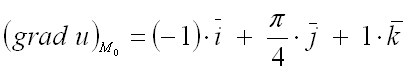
6. Найти градиент функции
в точке 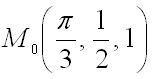
Ответ:
.
Градиент функции
Как найти?
Постановка задачи
Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Градиент функции $ f(x,y,z) $ – это вектор, каждая координата которого является частной производной первого порядка этой функции:
$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$
- Берём частные производные первого порядка от функции $ f(x,y,z) $:
$$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
$$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$ - Подставляем, полученные данные в формулу градиента функции:
$$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$
Примеры решений
| Пример 1 |
| Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $ |
| Решение |
|
Находим частные производные первого порядка функции трёх переменных: Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ grad f = (1,1,1) $$ |
| Пример 2 |
| Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $ |
| Решение |
|
Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$ |
| Ответ |
| $$ grad f = (3,1,frac{pi}{2}) $$ |
Как найти градиент функции
Градиент функции – векторная величина, нахождение которой связано с определением частных производных функции. Направление градиента указывает путь наискорейшего роста функции от одной точки скалярного поля к другой.
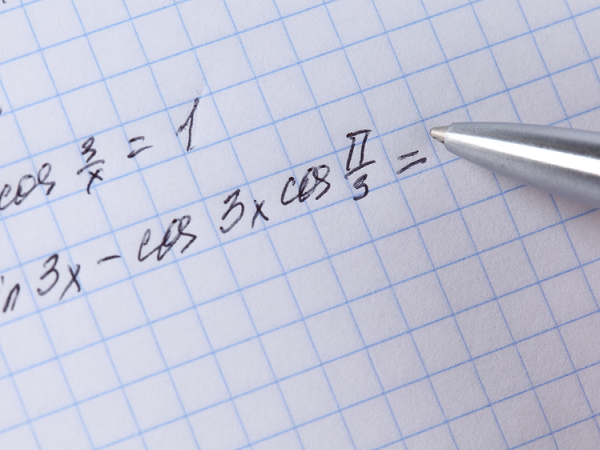
Инструкция
Для решения задачи на градиент функции используются методы дифференциального исчисления, а именно нахождение частных производных первого порядка по трем переменным. При этом предполагается, что сама функция и все ее частные производные обладают свойством непрерывности в области определения функции.
Градиент – это вектор, направление которого указывает направление максимально быстрого возрастания функции F. Для этого на графике выбираются две точки M0 и M1, которые являются концами вектора. Величина градиента равна скорости возрастания функции от точки M0 к точке M1.
Функция дифференцируема во всех точках этого вектора, следовательно, проекциями вектора на координатных осях являются все ее частные производные. Тогда формула градиента выглядит следующим образом:grad = (∂F/∂х)•i + (∂F/∂y)•j + (∂F/∂z)•k, где i, j, k – координаты единичного вектора. Иными словами, градиент функции – это вектор, координатами которого являются ее частные производные grad F = (∂F/∂х, ∂F/∂y, ∂F/∂z).
Пример1.Пусть задана функция F = sin(х•z²)/y. Требуется найти ее грaдиент в точке (π/6, 1/4, 1).
Решение.Определите частные производные по каждой переменной: F’_х = 1/y•соs(х•z²)•z²;F’_y = sin(х•z²)•(-1)•1/(y²);F’_z = 1/y•соs(х•z²)•2•х•z.
Подставьте известные значения координат точки:F’_x = 4•соs(π/6) = 2•√3; F’_y = sin(π/6)•(-1)•16 = -8; F’_z = 4•соs(π/6)•2•π/6 = 2•π/√3.
Примените формулу градиента функции:grаd F = 2•√3•i – 8•j + 2•π/√3•k.
Пример2.Найдите координаты градиента функции F = y•arсtg (z/x) в точке (1, 2, 1).
Решение.F’_х = 0•аrсtg (z/х) + y•(аrсtg(z/х))’_х = y•1/(1 + (z/х)²)•(-z/х²) = -y•z/(х²•(1 + (z/х)²)) = -1;F’_y = 1•аrсtg(z/х) = аrсtg 1 = π/4;F’_z = 0•аrсtg(z/х) + y•(аrсtg(z/х))’_z = y•1/(1 + (z/х)²)•1/х = y/(х•(1 + (z/х)²)) = 1.grаd = (-1, π/4, 1).
Видео по теме
Источники:
- нахождение градиента
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.