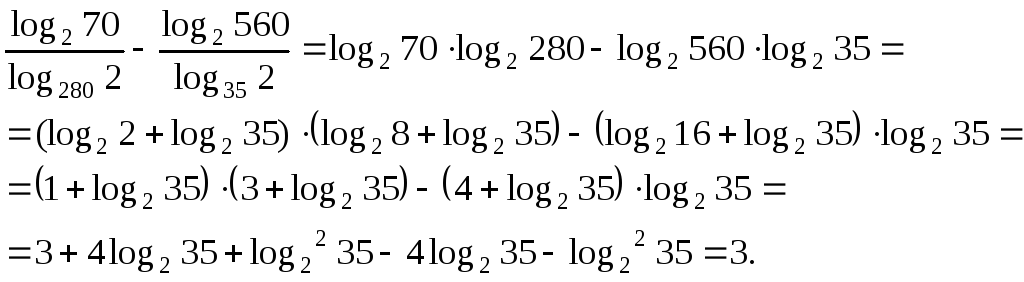§4. Рациональные неравенства. Метод интервалов.
В 9-м классе изучается метод интервалов прежде всего для многочленов. Он основан на том, что
а) двучлен `(x-a)` положителен при `x > a` и отрицателен при `x < a`, т. е. меняет знак при переходе через точку `a`,
б) квадрат двучлена `(x-a)^2` при переходе через точку `a` знак не меняет,
в) квадратный трёхчлен `x^2+px+q`, `p^2-4q < 0`, имеющий положительный коэффициент при `x^2` и отрицательный дискриминант, всегда положителен и может быть опущен при решении любого неравенства.
Заметим, что:
1) двучлен `(x-a)` в любой нечётной степени `(x-a)^(2n-1)`, n∈ℕ ninmathbb{N} ведёт себя так же, как и `(x-a)`,
2) двучлен `(x-a)` в любой чётной степени `(x-a)^(2n)`, n∈ℕ ninmathbb{N} ведёт себя так же, как и `(x-a)^2`,
Важно, что при переходе через точку `a`, может изменить знак только один множитель `(x-a)^(2k-1)`, а выражение `(x-b)^(2n-1)`, b≠a, bneq a, при переходе через `a` ни при каком `n` знак не меняет.
Прежде чем расставлять знаки, необходимо все многочлены записать правильно. Это значит, что во всех скобках коэффициенты при старшей степени переменной должны быть положительны, множители при произведениях в числителе и знаменателе тоже положительны – при больших `x` (когда `x` больше самого большого корня) многочлен всегда принимает положительные значения.
Итак, сформулируем
1. Проверяем, все ли множители записаны «правильно».
2. Находим корни числителя и знаменателя.
3. Представляем числитель и знаменатель в виде произведения неприводимых множителей, т. е. множителей вида `(x-a)^k` (все квадратные трёхчлены, имеющие отрицательный дискриминант, не записываем – их «опускаем»).
4. Наносим на числовую ось корни числителя (точками, если неравенство нестрогое, или «дырками», если неравенство строгое) и знаменателя (в любом неравенстве «дырками»).
5. Расставляем знаки дроби в промежутках между корнями, учитывая, что многочлен меняет знак при переходе через точку `a`, если в многочлене стоит `(x-a)^{2n-1}`, `ninN`
и не меняет знак, если в многочлене стоит `(x-a)^{2n}`, `ninN`.
6. Отмечаем прямоугольниками решение заданного неравенства и «снимаем» с рисунка ответ. При этом помним, что,
а) если неравенство строгое, то решением являются открытые промежутки;
б) если неравенство нестрогое, то к предыдущим решениям добавляются все «точки».
Когда говорим: Решим неравенство методом интервалов, – имеется в виду, что будут выполнены именно вышеприведённые действия.
Метод интервалов затем распространяется на рациональные функции.
Рациональной называется функция, которая может быть представлена в виде частного двух многочленов, т. е. в виде `{P(x)}/{Q(x)}`.
Например, функции `y=x-2`, `y={x^3-x+5}/{x+4}` – рациональные, а функция `y=sqrt(5x)` не является рациональной – она называется иррациональной.
Неравенства называются рациональными, если их правые и левые части являются рациональными функциями.
Рациональные неравенства чаще всего решаются сравнением с нулём, т. е. решаются неравенства вида `{P(x)}/{Q(x)}>0(<0)`.
Заметим, что дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель имеют одинаковые (противоположные) знаки, т. е.
`{P(x)}/{Q(x)}>0(<0)hArrP(x)Q(x)>0(<0)`,
поэтому метод интервалов применяется к дроби точно так же, как и к многочленам.
В школе принято писать для дроби ОДЗ: `Q(x)!=0`, но это является совершенно излишним. В самом алгоритме решения таких неравенств учитывается условие, что знаменатель не равен `0` – нули знаменателя отмечаются всегда кружочками («дырками»). Именно поэтому ОДЗ для рациональной дроби не пишут.
Некоторые учащиеся после нахождения ОДЗ даже «бросают» знаменатель. Они не понимают, что решение зависит не от того, равен или не равен `0` знаменатель, а от того, где знаменатель положителен, а где отрицателен.
При применении этого метода интервалов нет необходимости в рассмотрении «пробных» точек.
Найдите наименьшую длину промежутка, в котором расположены все решения неравенства 2-x54x+5≥0dfrac{displaystyledfrac{2-x}5}{4x+5}geq0.
Переписываем наше неравенство в правильном виде:
2-x54x+5≥0⇔x-2(x+54)≤0dfrac{displaystyledfrac{2-x}5}{4x+5}geq0Leftrightarrowdfrac{x-2}{(x+{displaystyledfrac54)}}leq0
и применяем метод интервалов – рис. 1.
| Рис. 1 |
C рисунка снимаем ответ.
`3,25`.
Заметим, что на нашей картинке нет никаких «змеек». Такой способ отмечать решение неравенства (который, с непривычки, некоторые отвергают, не попробовав) имеет преимущество, потому что он выделяет именно решение, а, кроме того, он даёт возможность «красиво» решать системы неравенств.
Решите систему неравенств
$$left{begin{array}{l}left(x-1right)left(x+dfrac14right)left(x+dfrac18right)geq0,\dfrac{left(x-2right)left(x-{displaystyledfrac{51}{50}}right)}{left(x+{displaystyledfrac3{16}}right)x}<0.end{array}right.$$
Здесь очень «плохие» пробные точки – дробные и близкие. Это сделано специально, чтобы привыкнуть их использовать.
Решаем сначала первое неравенство: наносим на числовую ось нули точками, т. к. неравенство нестрогое.
Теперь расставим знаки. Замечаем, что при больших `x` все множители положительны. При переходе через точку `x=1` функция меняет знак, т. к. `(x-1)` входит в нечётной (первой) степени. По этой же причине при переходе и через остальные точки функция опять меняет знак (рис. 2).
| Рис. 2 |
Теперь отметим «прямоугольниками» решение неравенства (рис. 3).
| Рис. 3 |
Теперь решаем второе: наносим на числовую ось нули и числителя, и знаменателя кружочками (дырками), т. к. неравенство строгое. Получаем рис. 4.
| Рис. 4 |
Теперь надо обе картинки поместить на одну ось. Надо ли соблюдать масштаб? А зачем? Не надо. Ведь нас интересует только взаимное расположение точек относительно друг друга, а расстояния между ними никакой роли не играют.
Теперь заштриховываем общие части прямоугольников – отлично виден ответ (рис. 5).
| Рис. 5 |
`x in(-3/16;-1/8]uu(51/50;2)`.
Найдите наименьшую длину промежутка, в котором расположены все решения неравенства
`(x-1)^2(x+1,5)^3(x-12)(x+2)^4(x-25)^8<=0`.
При решении неравенств, левая часть которых содержит чётные степени, можно поступать по-разному.
Первый способ
Левая часть уже записана правильно, корни видны сразу. Отмечаем их точками на числовой оси, а затем по вышеприведённым правилам расставляем знаки и отмечаем решение прямоугольниками – рис. 6.
| Рис. 6 |
С рисунка снимаем ответ, что `x in{-2;25}uu[-1,5;12]`. Отсюда следует, что наименьшая длина промежутка равна `25-(-2)=27`.
Второй способ
Можно заранее учесть, что бином `(x-a)^{2k}` принимает либо значение, равное `0`, либо положительно на всей числовой оси – поэтому можно записать в решение `x=a`, а бином «опустить», т. к. он не влияет на знак оставшегося выражения:
`(x-1)^2(x+1,5)^3(x-12)(x+2)^4(x-25)^8<=0 iff`
⇔x=1,x=-2,x=25,(x+1,5)(x-12)≤0⇔x∈-2;25∪-1,5;12.Leftrightarrowleft[begin{array}{l}begin{array}{c}x=1,\x=-2,\x=25,end{array}\(x+1,5)(x-12)leq0end{array}right.Leftrightarrow xinleft{-2;25right}cupleft[-1,5;12right].
`27`.
Решите неравенство `x<={8x-2}/{x+5}`.
`x<={8x-2}/{x-5}hArr{x^2-3x+2}/{x+5}<=0hArr{(x-1)(x-2)}/{x+5}<=0`
| Рис. 7 |
Из рис. 7 следует ответ
`(-oo;-5)uu[1;2]`.
Найти все пары целых чисел `x`, `y`, для которых верны неравенства
$$left{begin{array}{l}3y-2x<45,\x+y>24,\3x-y<3.end{array}right.$$
Запишем систему в стандартном виде (для сравнения с нулём)
$$left{begin{array}{l}3y-2x-45<0,\-x-y+24<0,\3x-y-3<0.end{array}right.$$
Заметим, что `y` входит в первое неравенство со знаком `« + »`, а во второе и третье со знаком `« – »`. Поэтому умножим сначала второе и третье неравенства на `3` (получились равносильные неравенства), а затем заменим второе и третье неравенства их суммами с первым – таким образом, мы исключим `y`. Итак,
$$left{begin{array}{l}3y-2x-45<0,\-x-y+24<0,\3x-y-3<0,end{array}right.Rightarrow$$
$$Rightarrowleft{begin{array}{l}3y-2x-45<0,\-3x-3y+72+3y-2x-45=-5x+27<0Leftrightarrow x>dfrac{27}5,\9x-3y-9+3y-2x-45=7x-54<0Leftrightarrow x<dfrac{54}7end{array}right.Rightarrow$$
(учтём, что мы ищем целые решения) ⇒x=6,7.Rightarrow x=left[begin{array}{l}6,\7.end{array}right.
Подставим последовательно найденные значения `x` в систему.
$$x=6Rightarrowleft{begin{array}{l}3y-57<0,\-y+18<0,\15-y<0end{array}right.Rightarrowvarnothing.$$
$$x=7Rightarrowleft{begin{array}{l}3y-59<0,\-y+17<0,Rightarrow y=19,\-y+18<0.end{array}right.$$
`(7,19)`.
Решаем первое двойное неравенство
Решаем второе неравенство.
Важно обратить внимание на первую скобку, в ней нет аргумента, но нужно посмотреть, больше или меньше она нуля.
внесем двойку и тройку под корни и увидим что √8-√9 <0 => (2√3-3)<0
Теперь смело отметаем эту скобку, но при решении 5x-3 помним, что знак нужно будет поменять.
И так вышли решения:
x<1; x>-0,5; x<0,6
Объединяем их и получаем:
Длинна интервала находится как разность правой и левой границы
Ответ: 1,1.
Неравенства. Логарифмы.
Логарифмические уравнения и
Неравенства
Показательная функция:
,
где
.
Свойства
показательной функции
1. Область
определения:
.
2. Область значений:
.
3. При
функция
монотонно возрастает, а при
– монотонно убывает.
4. График
функции
имеет вид
Логарифмом числа
по
основанию
,
называется
число
,
для которого
.
.
Основные
свойства логарифмов
1.
2.
.
3. Основное логарифмическое тождество:
,
.
4.
.
38
5.
.
6.
.
7.
8.
,
.
Логарифмическая
функция:
Свойства логарифмической
функции
1. Область определения: . 2. Область значений: . 3. При функция монотонно возрастает, а при – монотонно убывает. 4. График функции имеет вид
Показательные
уравнения
Решение показательных уравнений
основано на свойстве степеней: две
степени с одним и тем же положительным
и отличным от единицы основанием равны
тогда и только
39
тогда,
когда равны их показатели.
1.
.
2.
3.
.
4.
Уравнение вида
,
где
,
,
,
с помощью подстановки
сводится к квадратному уравнению
.
Логарифмические
уравнения
1.
Уравнение
,
где
,
равносильно
уравнению
.
2.
3.
Решение
простейших показательных и
логарифмических
неравенств основано
на свойствах монотонности показа-
тельной
и логарифмической функций:
при
:
40
при
:
Пример 1. Решить
уравнение:
.
Решение. Так
как
и

то исходное уравнение равносильно
уравнению
,
откуда
Ответ:
.
Пример
2. Решить уравнение:
.
Решение.
Ответ:.
Пример 3. Решить уравнение:
.
Решение.
Разделив обе части исходного уравнения
на
(
при всех
),
получим равносильное ему уравнение :
;
.
41
Обозначив
,
,
последнее уравнение запишем в виде
.
Корнями
этого уравнения являются
и
.
Учитывая, что
положительное
число, получим:
.
Тогда:
;.
Ответ:
.
Пример 4.
Вычислить
.
Решение.
,
.
Поэтому
.
Ответ:
1125.
Пример 5.
Вычислить
.
Решение.
Ответ:
3.
Пример 6.
Вычислить

42
Решение.
;
.
Следовательно,

Ответ: –
4.
Пример 7. Решить
уравнение:
Решение. Так
как
,
то исходное уравнение можно записать
в виде:
.
(1)
ОДЗ уравнения
(1) :
т. е.
(2)
На
ОДЗ (2) уравнение (1) равносильно уравнению
Корнями последнего уравнения являются
и
,
из которых
входит в ОДЗ (2), а
нет.
Поэтому единственным корнем исходного
уравнения является число 2.
Ответ
:
.
43
Пример
8. Решить
уравнение:
.
(3)
Решение.
ОДЗ уравнения (3):

Обозначим
.
Тогда
и
уравнение (3) принимает вид:
.
Корни
последнего уравнения:
и
.
Так как
,
то
.
Ответ:
.
Пример 9. Найти
сумму корней уравнения:
.
Решение. ОДЗ
уравнения:
.
Прологарифмируем обе части данного
уравнения по основанию 10 :
;
,
т.е.
.
Обозначив
,
получим квадратное уравнение
,
корни которого –
.
.
.
Ответ: 110.
Пример 10. Найти наименьшее целое
значение
,
удовлет-
воряющее неравенству
.
Решение. Поскольку
,
то данное не-
равенство равносильно
неравенству
. Обозначив
,
получим
.
Вернемся
к переменной
:
,
откуда
44
.
Наименьшее целое значение
из этого интерва-ла равно
.
Ответ:
.
Пример 11.
Найти число целых решений неравенства
.
Решение.
Поскольку
,
,
то данное неравенство равносильно
неравенству
.
Полученный интервал содержит целые
числа
.
Ответ:
4.
Пример
12. Найти
длину интервала решений неравенства:
.
(4)
Решение.
ОДЗ
неравенства (4):

(5)
На ОДЗ неравенство (4) равносильно
неравенству
.
Решая последнее неравенство методом
интервалов и учитывая ОДЗ (5) , получим,
что решением не-
равенства
(4) является интервал
.
Длина этого интер-
вала:
.
Ответ:
.
45
Пример
13. Найти
длину интервала решений неравенства
.
Решение.
ОДЗ неравенства:
.
Так как
,
то
исходное
неравенство можно записать в виде
,
откуда
.
Длина этого интервала:
.
Ответ:
.
Пример
14. Найти
область определения функции

Решение. Так
как
,
то область определения данной функции
состоит из
,
удовлетворяющих системе:

Ответ:
46
ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.
Решить уравнение:
а)
;
(Ответ: 10)
б)
;
(Ответ: 1)
в)
;
(Ответ: 5)
г)
;
(Ответ: 1)
д)
;
(Ответ: 1,5)
е)
;
(Ответ: 2)
ж)
(Ответ:
)
2.
Найти больший корень уравнения:
а)
;
(Ответ:
6)
б)
.
(Ответ: 3)
3.
Найти наибольшее целое значение
,
удовлетворяющее не-
равенству:
а);
(Ответ:
3)
б).
(Ответ:
–2)
4.
Найти наименьшее целое значение
,
удовлетворяющее
неравенству
а)
;
(Ответ: 2)
б)
;
(Ответ: –
2)
47
в)
.
(Ответ: 3)
5.
Найти число целых решений неравенства
.
(Ответ: 8)
6.
Вычислить:
а)
;
(Ответ: – 40)
б)
;
(Ответ: 19)
в)
;
(Ответ: 13)
г)
;
(Ответ: 1)
д)
;
(Ответ: 1)
е)
.
(Ответ: 4)
7.
Решить уравнение:
а)
;
(Ответ: 3)
б)
;
(Ответ: 1)
в)
;
(Ответ: 50)
г)
;
(Ответ:
)
д)
.
(Ответ: 4)
48
8.
Найти сумму корней уравнения:
.
(Ответ: 84)
9.
Найти больший корень уравнения:
а)
;
(Ответ:
625)
б).
(Ответ:
64)
10.
Найти наименьшее целое значение
,
удовлетворяющее
неравенству:
а)
;
(Ответ: 4)
б)
.
(Ответ: 2)
11.
Найти сумму целых решений неравенства:
а)
;
(Ответ: 6)
б)
;
(Ответ: 3)
в)
;
(Ответ: –1)
г)

(Ответ:
76)
12.
Найти наименьшее целое значение
из области определения функции
.
(Ответ: 512)
13.
Найти число целых значений
,
принадлежащих области определения
функции

(Ответ: 3)
49
14.
Найти длину интервала решений неравенства:
а)
;
(Ответ:
3,25)
б)
.
(Ответ: 1,5)
15.
Решить неравенство:
.
(Ответ:
)
16.
Найти наименьшее целое решение
неравенства:
.
(Ответ: 3)
50
Соседние файлы в папке MatSost (2) (1)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема урока. Введение
Напоминание: Мы решаем неравенство вида На прошлом уроке мы рассмотрели функцию
На примере подобной функции мы рассмотрели метод интервалов для решения рациональных неравенств и схематического построения графика функции.
Решение дробно-квадратичного неравенства
Вместо могут быть другие функции, например, дробно-линейные или дробно-квадратичные. Решение неравенств такого рода является нашей целью.
1. Решить неравенство
Это же неравенство может быть представлено в виде тогда нужно вначале разложить на множители числитель и знаменатель дроби.
1. Рассмотрим функцию
2. Область определения:
3. Найдем нули функции
4. Выделим интервалы знакопостоянства.
5. Находим знак функции на каждом интервале.
Можно проверить знаки по методу пробной точки. Например, на промежутке На остальных промежутках аналогично.(Рис.1)
Теперь возвращаемся к неравенству
Ответ:
Рассмотрим некоторые сопутствующие задачи.
Найти наименьшее решение неравенства.
Ответ:
Найти число натуральных решений неравенства
Ответ: 2.
Найти длину интервалов, составляющих множество решений неравенства.
Ответ:2.
Решение дробно-линейных неравенств
Мы рассмотрели метод интервалов на примере дробно-квадратичного рационального неравенства. Рекомендуется самостоятельно построить эскиз графика функции для данного примера.
2. Решить неравенство:
Эквивалентными преобразованиями приведем неравенство к нужному виду.
Множество решений этого неравенства совпадает со множеством решений исходного неравенства
Неравенство такого вида мы уже умеем решать методом интервалов.
1.
2. Область допустимых значений
3. Нули функции
4. Определяем интервалы знакопостоянства.
4 – выколотая точка, т.к. при функция не существует, изобразим это на графике пунктирной линией.
5. Расставим знаки на промежутках. Самостоятельно можно проверить знаки методом пробной точки (Рис.2).
Теперь можно вернуться к неравенству и выбрать интервалы, удовлетворяющие заданным условиям.
Ответ:
Мы привели исходное неравенство к дробно-линейному виду. Самостоятельно можно построить эскиз графика функции.
3. Решить неравенство
При решении данного неравенства может быть допущена грубая ошибка. Решать его методом умножения обеих частей на категорически нельзя, будет потеряно множество решений!
Можно умножить обе части неравенства на положительное число, тогда знак неравенства останется прежним. Можно умножить на отрицательное число, тогда знак неравенства поменяется. Но умножать на мы не можем, т.к. не знаем его знака.
Поэтому решаем неравенство методом эквивалентных преобразований.
1. Рассмотрим функцию
2. Область определения
3. Нули функции
4. Определим интервалы знакопостоянства.
Точка 0 выколотая, в ней функция не существует, отметим это на графике пунктирной линией.
5. Расставим знаки на интервалах (Рис. 3).
Возвращаемся к неравенству.
Ответ:
Вывод
Мы рассмотрели решение неравенств методом интервалов. В качестве функции выступала дробь, в числителе и знаменателе либо линейная, либо квадратичная функция.
Мы и дальше будем использовать метод интервалов при решении сложных рациональных неравенств.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. – М., 2011. – 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Портал Естественных Наук (Источник).
2. Портал Естественных Наук (Источник).
3. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).
4. Виртуальный репетитор (Источник).
5. Центр образования «Технология обучения» (Источник).
6. Раздел College.ru по математике (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 28(б,в); 29(б,в); 35(а,б); 37(б,в); 38(а).
Вопросец по неравенству
Мастер
(2384),
закрыт
14 лет назад
Аркадий Редько
Просветленный
(23856)
14 лет назад
1.Найдем область определения выражения:
x+18>0 x>-18; (x-2)(x+2) не равен 0, т. е. х не равен 2 или х не равен -2
2. навйдем ” нули” ,т. е. приравняем числитель к 0. Получим, что корень квадратный из х^2+5=5-x, возведем обе частив квадрат и получим корень х=2 Сделаем проверку, не посторонний ли это корень. Все в порядке.
3. Теперь все эти данные выставим на координатную прямую и получим интервалы
х>-18 x=2 x=-2 от -18 до -2 от -2 до 2 от 2 до плюс бесконечности.
В каждом интервале поставим знаки, которые соответствуют данному выражению.
В первом будет отрицательный, во втором положительный и в третьем положительный. Ваш ответ : ( -18; -2) . Под длиной, видимо, подразумевается разность координат, т. е. – 2 – ( -18)=-2+18 =16
Источник: личные знания