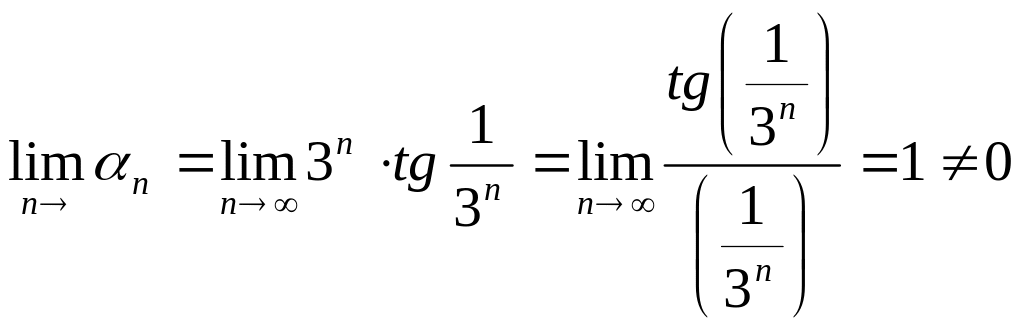Степенным
рядом называется функциональный ряд
вида
,
(10)
где
коэффициенты
–
действительные числа.
Основное
свойство степенных рядов состоит в том,
что если ряд (10) сходится при
,
то он сходится ( и притом абсолютно) при
всяком значении х, удовлетворяющем
неравенству
(теорема
Абеля). Следствием теоремы Абеля является
существование для всякого степенного
ряда (10) интервала сходимости
с центром в точке х=а,
внутри которого ряд (10) сходится абсолютно
; при
ряд (10) расходится. Радиус
сходимости R
(т.е. половина длины интервала сходимости)
может быть в частных случаях равен также
0 и ∞. В конечных точках
интервала сходимости возможна как
сходимость, так и расходимость ряда
(10). Интервал сходимости определяют
обычно с помощью признаков Даламбера
или Коши, применяя их к ряду, составленному
из абсолютных величин членов исходного
ряда . Но если
или
,
(11)
где
и
– коэффициенты соответственно n-го
и (n+1)-го
членов ряда (10), то радиус сходимости
ряда (10) определяется по формуле
.
Однако пользоваться формулами (11) следует
весьма осторожно. Если L=0,
то R=∞
и ряд (10) сходится при
.
Если L=∞,
то R=0
и ряд (10) расходится при любом х, кроме
х=0.
Пример
1. Найти
радиус и интервал сходимости
степенного
ряда
Решение.
Имеем коэффициенты ряда
.
Найдем число L
(см. формулы 11)
.
Следовательно, радиус сходимости R=5.
Интервал сходимости ряда
с центром в точке
или
есть
.
Исследуем поведение ряда в концевых
точках интервала:
При
х=8:
–
расходящийся гармонический ряд
При
х=-2:
– условно сходящийся (по Лейбницу).
Ответ:
R=5;
.
Пример
2. Исследовать
сходимость ряда
Решение.
Общий член
ряда имеет коэффициент
Находим
по формуле (11) число
.
Т.е.,
.
Значит, ряд расходится при
,
кроме х=0. В этом случае говорят, что ряд
всюду расходится.
Задание
14. Найти
область сходимости степенного ряда.
Задача
1.
Решение.
Имеем коэффициенты ряда
,
.
Находим число L
по одной из формул (11):
,
(т.к.
~
при бесконечно малых
).
Значит, радиус сходимости
,
интервал сходимости
с центром в точке
.
Откуда получаем
,
или
.
В концевых точках интервала (-8;-2) исследуем
поведение ряда: При х=-2 имеем ряд
– расходящийся, т.к.
.
При х=-8 имеем знакочередующийся ряд
,
который также расходится, ибо не выполнено
условие
.
Ответ:
Интервал сходимости (-8;-2), R=3.
Задача
2.
Решение.
Область
сходимости данного степенного ряда
будем находить по одной из формул (9),
т.к. этот ряд содержит члены только с
нечетными степенями (х-7) и пользоваться
напрямую формулами (11) нельзя, поэтому
что бесконечно много коэффициентов
обращается в ноль и пределы в правых
частях формул (11) не существуют. Имеем
.
Находим
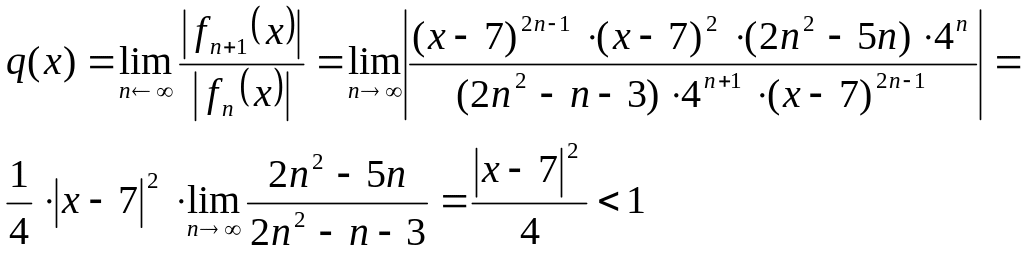
должно
быть для сходимости ряда по признаку
Даламбера.
Решая
неравенство
,
получаем
,
или
,
откуда интервал сходимости степенного
ряда
(5;9)
с центром в точке
и радиусом R=2.
Рассмотрим поведение ряда в концевых
точках: При х=9 получаем знакоположительный
числовой ряд
,
где общий член
~
и по второму (предельному) признаку
сравнения сходится, ибо сходится ряд
(p=2>1).
При
х=5 получаем ряд
с
общим членом
,
который также сходится.
Ответ:
Интервал сходимости
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
01.05.20221.51 Mб0Учебники 60167.doc
- #
01.05.20221.53 Mб0Учебники 60168.doc
- #
- #
- #
- #
- #
01.05.20221.56 Mб0Учебники 60172.doc
- #
- #
- #
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 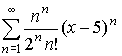
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Пример. 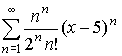
Решение.
Общий вид степенного ряда 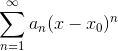
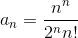
Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
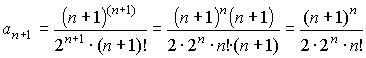
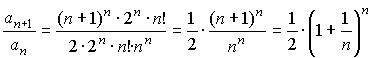
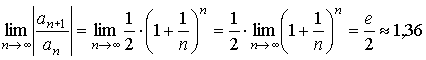
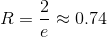
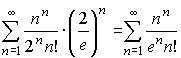
Для исследования сходимости этого ряда используем формулу Стирлинга 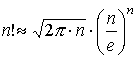
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при 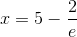
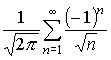
Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
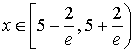
Как найти интервал сходимости
Степенной ряд – частный случай функционального ряда, члены которого – степенные функции. Их широкое распространение связано с тем, что при выполнении ряда условий они сходятся к заданным функциям и являются наиболее удобным аналитическим аппаратом для их представления.

Инструкция
Степенной ряд – это частный случай функционального ряда. Он имеет вид 0+c1(z-z0)+c2(z-z0)^2+…+cn(z-z0)^n+… . (1)Если сделать подстановку x=z-z0, то этот ряд примет вид c0+c1x+c2x^2+…+cn(x^n)+… . (2)
В данном случае ряды вида (2) более удобны для рассмотрения. Очевидно, что любой степенной ряд сходится при х=0. Множество точек, в которых ряд является сходящимся (область сходимости), можно найти опираясь на теорему Абеля. Из нее следует, что если ряд (2) является сходящимся в точке x0≠0, то он сходится для всех х, удовлетворяющих неравенству |x|
Соответственно, если в некоторой точке х1 ряд расходится, то это наблюдается при всех х, для которых |x1|>|b|. Иллюстрация рис.1, где х1 и х0 выбраны большими нуля, позволяет понять, что все х1>x0. Поэтому при их сближении неминуемо возникнет ситуация х0=х1. В этом случае ситуация со сходимостью, при прохождении слившихся точек (назовем их –R и R) меняется скачкообразно. Поскольку геометрически R длина, то число R≥0 называется радиусом сходимости степенного ряда (2). Интервал (-R,R) называется интервалом сходимости степенного ряда. Возможно и R=+∞. При x=±R ряд становится числовым и его анализ производится на основе сведений о числовых рядах.
Для определения R ряд исследуется на абсолютную сходимость. То есть составляется ряд из абсолютных величин членов исходного ряда. Исследования можно проводить на основе признаков Даламбера и Коши. При их применении отыскиваются пределы, которые сравниваются с единицей. Поэтому предел равный единице достигается при х=R. При решении по признаку Даламбера сначала отыскивается предел, представленный на рис. 2а. Положительное число х, при котором этот предел равен единице, будет являться радиусом R (см. рис. 2b). При исследовании ряда по радикальному признаку Коши формула для вычисления R примет вид (см. рис. 2c).
Формулы, представленные на рис. 2 применяются при условии, что рассматриваемые пределы существуют. Для степенного ряда (1) интервал сходимости записывается в виде (z0-R, z0+R).
Источники:
- Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов. Т.2. – М.: Наука, 1976. – 576 с.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Степенные ряды. Интервал сходимости
Определение:
степенным рядом называется функциональный ряд вида
, где
– постоянные
числа, называемые коэффициентами ряда.
Областью
сходимости степенного ряда всегда является некоторый интервал.
Теорема (Абеля):
1)
Если
степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно
сходится при всяком значении х, для которого
;
2)
Если
ряд расходится при некотором значении , то он расходится при всяком х, для
которого
Теорема:
Областью сходимости степенного ряда
является интервал с цетром в начале координат.
Определение:
Интервалом
сходимости степенного ряда называется интервал от –R
до +R, что для всякой точки х, лежащей внутри этого
интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд
расходится. Число R называется
радиусом сходимости степенного ряда.
На концах
интервала вопрос о сходимости ряда решается индивидуально для каждого конретного ряда.
Отметим , что у некоторых рядов интервал сходимости вырождается в
точку (R=0), у других охватывает всю ось ОХ (R=).
Радиус сходимости
степенного ряда определяется по формуле

или
Примеры:
Пример1:
Найти область
сходимости ряда
Решение.
Радиус
сходимости степенного ряда можно найти по формуле: 
Т.к.



Итак,
радиус сходимости ряда . Т.о. данный степенной ряд
расходится, при
.
Исследуем
сходимость ряда при .
Пусть. Подставим
в заданный
степенной ряд и получим ряд

Итак, областью
сходимости данного степенного ряда является значение .
Пример2:
Найти
область сходимости степенного ряда 
Решение.
Радиус
сходимости степенного ряда можно найти по формуле: 
Т.к.



Итак,
радиус сходимости ряда . Определим интервал сходимости данного степенного
ряда:
.
–
интервал сходимости степенного ряда. Исследуем сходимость ряда на концах
интервала сходимости.
Пусть
. Подставим
в заданный
степенной ряд и получим числовой ряд с положительными членами:
Получили расходящийся
обобщенный гармонический ряд.
Значит,
не принадлежит
области сходимости степенного ряда.
Пусть. Подставим
в заданный
степенной ряд и получим знакочередующийся ряд

Для
членов полученного ряда:
1)
2) , т.е.
В
соответствии с признаком Лейбница данный ряд сходится и принадлежит
области сходимости степенного ряда.
Итак, областью
сходимости данного степенного ряда является промежуток 
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
интервал:сходимости:sum_{n=0}^{infty}frac{x^{n}}{n!}
-
интервал:сходимости:sum_{n=1}^{infty}nx^{n}
-
интервал:сходимости:sum_{n=1}^{infty}frac{(x-3)^n}{n}
-
интервал:сходимости:sum_{n=0}^{infty}x^{n}
- Показать больше
Описание
Шаг за шагом найдите интервал сходимости степенного ряда
interval-of-convergence-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
The Art of Convergence Tests
Infinite series can be very useful for computation and problem solving but it is often one of the most difficult…
Read More
Введите Задачу
Сохранить в блокнот!
Войти