Вычисление длин кодов
Для
того чтобы закодировать сообщение нам
необходимо знать коды символов и их
длины. Как уже было отмечено в предыдущем
разделе, канонические коды вполне
определяются своими длинами. Таким
образом, наша главная задача заключается
в вычислении длин кодов.
Оказывается,
что эта задача, в подавляющем большинстве
случаев, не требует построения дерева
Хаффмана в явном виде. Более того,
алгоритмы использующие внутреннее (не
явное) представление дерева Хаффмана
оказываются гораздо эффективнее в
отношении скорости работы и затрат
памяти.
На
сегодняшний день существует множество
эффективных алгоритмов вычисления длин
кодов ([3],
[4]).
Мы ограничимся рассмотрением лишь
одного из них. Этот алгоритм достаточно
прост, но несмотря на это очень популярен.
Он используется в таких программах как
zip, gzip, pkzip, bzip2 и многих других.
Вернемся
к алгоритму построения дерева Хаффмана.
На каждой итерации мы производили
линейный поиск двух узлов с наименьшим
весом. Ясно, что для этой цели больше
подходит очередь приоритетов, такая
как пирамида (минимальная). Узел с
наименьшим весом при этом будет иметь
наивысший приоритет и находиться на
вершине пирамиды. Приведем этот алгоритм.
-
Включим
все кодируемые символы в пирамиду. -
Последовательно
извлечем из пирамиды 2 узла (это будут
два узла с наименьшим весом). -
Сформируем
новый узел и присоединим к нему, в
качестве дочерних, два узла взятых из
пирамиды. При этом вес сформированного
узла положим равным сумме весов дочерних
узлов. -
Включим
сформированный узел в пирамиду. -
Если
в пирамиде больше одного узла, то
повторить 2-5.
Будем
считать, что для каждого узла сохранен
указатель на его родителя. У корня дерева
этот указатель положим равным NULL. Выберем
теперь листовой узел (символ) и следуя
сохраненным указателям будем подниматься
вверх по дереву до тех пор, пока очередной
указатель не станет равен NULL. Последнее
условие означает, что мы добрались до
корня дерева. Ясно, что число переходов
с уровня на уровень равно глубине
листового узла (символа), а следовательно
и длине его кода. Обойдя таким образом
все узлы (символы), мы получим длины их
кодов.
Максимальная длина кода
Как
правило, при кодировании используется
так называемая кодовая
книга (CodeBook),
простая структура данных, по сути два
массива: один с длинами, другой с кодами.
Другими словами, код (как битовая строка)
хранится в ячейке памяти или регистре
фиксированного размера (чаще 16, 32 или
64). Для того чтобы не произошло переполнение,
мы должны быть уверены в том, что код
поместится в регистр.
Оказывается,
что на N-символьном алфавите максимальный
размер кода может достигать (N-1) бит в
длину. Иначе говоря, при N=256 (распространенный
вариант) мы можем получить код в 255 бит
длиной (правда для этого файл должен
быть очень велик: 2.292654130570773*10^53~=2^177.259)!
Ясно, что такой код в регистр не поместится
и с ним нужно что-то делать.
Для
начала выясним при каких условиях
возникает переполнение. Пусть частота
i-го символа равна i-му числу Фибоначчи.
Например: A-1,
B-1,
C-2,
D-3,
E-5,
F-8,
G-13,
H-21.
Построим соответствующее дерево
Хаффмана.
ROOT
/
/
/
/
H
/
/
/
G
/
/
/
F
/
/
/
E
/
/
/
D
/
/
/
C
/
/
A
B
Такое
дерево называется вырожденным.
Для того чтобы его получить частоты
символов должны расти как минимум как
числа Фибоначчи или еще быстрее. Хотя
на практике, на реальных данных, такое
дерево получить практически невозможно,
его очень легко сгенерировать искусственно.
В любом случае эту опасность нужно
учитывать.
Эту
проблему можно решить двумя приемлемыми
способами. Первый из них опирается на
одно из свойств канонических кодов.
Дело в том, что в каноническом коде
(битовой строке) не более [log2N]
младших бит могут быть ненулями. Другими
словами, все остальные биты можно вообще
не сохранять, т.к. они всегда равны нулю.
В случае N=256 нам достаточно от каждого
кода сохранять лишь младшие 8 битов,
подразумевая все остальные биты равными
нулю. Это решает проблему, но лишь
отчасти. Это значительно усложнит и
замедлит как кодирование, так и
декодирование. Поэтому этот способ
редко применяется на практике.
Второй
способ заключается в искусственном
ограничении длин кодов (либо во время
построения, либо после). Этот способ
является общепринятым, поэтому мы
остановимся на нем более подробно.
Существует
два типа алгоритмов ограничивающих
длины кодов. Эвристические (приблизительные)
и оптимальные. Алгоритмы второго типа
достаточно сложны в реализации и как
правило требуют больших затрат времени
и памяти, чем первые. Эффективность
эвристически-ограниченного кода
определяется его отклонением от
оптимально-ограниченного. Чем меньше
эта разница, тем лучше. Стоит отметить,
что для некоторых эвристических
алгоритмов эта разница очень мала ([6],
[7],
[8]),
к тому же они очень часто генерируют
оптимальный код (хотя и не гарантируют,
что так будет всегда). Более того, т.к.
на практике переполнение случается
крайне редко (если только не поставлено
очень жесткое ограничение на максимальную
длину кода), при небольшом размере
алфавита целесообразнее применять
простые и быстрые эвристические методы.
Мы
рассмотрим один достаточно простой и
очень популярный эвристический алгоритм.
Он нашел свое применение в таких
программах как zip, gzip, pkzip, bzip2 и многих
других.
Задача
ограничения максимальной длины кода
эквивалентна задаче ограничения высоты
дерева Хаффмана. Заметим, что по построению
любой нелистовой узел дерева Хаффмана
имеет ровно два потомка. На каждой
итерации нашего алгоритма будем уменьшать
высоту дерева на 1. Итак, пусть L –
максимальная длина кода (высота дерева)
и требуется ограничить ее до L/
< L. Пусть далее RNi
самый правый листовой узел на уровне
i, а LNi
– самый левый.
Начнем
работу с уровня L. Переместим узел RNL
на место своего родителя. Т.к. узлы идут
парами нам необходимо найти место и для
соседного с RNL
узла. Для этого найдем ближайший к L
уровень j, содержащий листовые узлы,
такой, что j < (L-1). На месте LNj
сформируем нелистовой узел и присоединим
к нему в качестве дочерних узел LNj
и оставшийся без пары узел с уровня L.
Ко всем оставшимся парам узлов на уровне
L применим такую же операцию. Ясно, что
перераспределив таким образом узлы, мы
уменьшили высоту нашего дерева на 1.
Теперь она равна (L-1). Если теперь L/
< (L-1), то проделаем то же самое с уровнем
(L-1) и т.д. до тех пор, пока требуемое
ограничение не будет достигнуто.
Вернемся
к нашему примеру, где L=5. Ограничим
максимальную длину кода до L/=4.
ROOT
/
/
/
/
H
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/ C
E
/
/
/
/
/
A
D
G
/
/
B
F
Видно,
что в нашем случае RNL=F,
j=3, LNj=C.
Сначала переместим узел RNL=F
на место своего родителя.
ROOT
/
/
/
/
H
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/ C
E
/
/
/
/
F
A
D
G
B
(непарный узел)
Теперь
на месте LNj=C
сформируем нелистовой узел.
ROOT
/
/
/
/
H
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/ / E
/
/ /
/
/ /
F
A
D
G
?
?
B
(непарный узел)
C
(непарный узел)
Присоединим
к сформированному узлу два непарных: B
и C.
ROOT
/
/
/
/
H
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/
/ / E
/
/ /
/
/ /
F
A
D
G
B
C
Таким
образом, мы ограничили максимальную
длину кода до 4. Ясно, что изменив длины
кодов, мы немного потеряли в эффективности.
Так сообщение S, закодированное при
помощи такого кода, будет иметь размер
92 бита, т.е. на 3 бита больше по сравнению
с минимально-избыточным кодом.
Ясно,
что чем сильнее мы ограничим максимальную
длину кода, тем менее эффективен будет
код. Выясним насколько можно ограничивать
максимальную длину кода. Очевидно что
не короче [log2N]
бит.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«Цель этого курса — подготовить вас к вашему техническому будущему.»
 Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 28 (из 30) глав. И ведем работу над изданием «в бумаге».
Теория кодирования — I
Рассмотрев компьютеры и принцип их работы, сейчас мы будем рассматривать вопрос представления информации: как компьютеры представляют информацию, которую мы хотим обработать. Значение любого символа может зависит от способа его обработки, у машины нет никакого определенного смысла у используемого бита. При обсуждении истории программного обеспечения 4 главе мы рассматривали некоторый синтетический язык программирования, в нём код инструкции останова совпадал с кодом других инструкций. Такая ситуация типична для большинства языков, смысл инструкции определяется соответствующей программой.
Для упрощения проблемы представления информации рассмотрим проблему передачи информации от точки к точке. Этот вопрос связан с вопросом сохранения информация. Проблемы передачи информации во времени и в пространстве идентичны. На рисунке 10.1 представлена стандартная модель передачи информации.
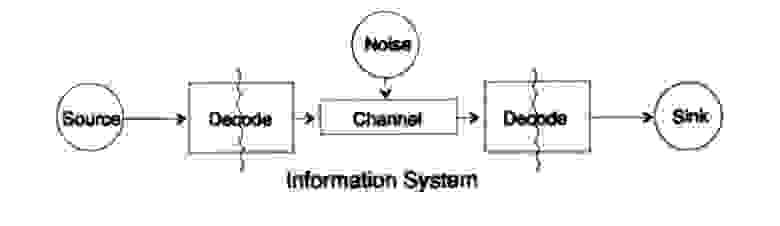
Рисунок 10.1
Слева на рисунке 10.1 находится источник информации. При рассмотрении модели нам неважна природа источника. Это может быть набор символов алфавита, чисел, математических формул, музыкальных нот, символов, которыми мы можем представить танцевальные движения — природа источника и значение хранящихся в нём символов не является частью модели передачи. Мы рассматриваем только источник информации, с таким ограничением получается мощная, общая теория, которую можно распространить на многие области. Она является абстракцией из многих приложений.
Когда в конце 1940 годов Шеннон создал теорию информации, считалось, что она должна была называться теорией связи, но он настоял на термине информация. Этот термин стал постоянной причиной как повышенного интереса, так и постоянных разочарований в теории. Следователи хотели строить целые «теории информации», они вырождались в теории о наборе символов. Возвращаясь к модели передачи, у нас есть источник данных, которые необходимо закодировать для передачи.
Кодер состоит из двух частей, первая часть называется кодер источника, точное название зависит от типа источника. Источникам разных типов данных соответствуют разные типы кодеров.
Вторая часть процесса кодирования называется кодирование канала и зависит от вида канала для передачи данных. Таким образом, вторая часть процесса кодирования согласована с типом канала передачи. Таким образом, при использовании стандартных интерфейсов данные из источника в начале кодируются согласно требованиям интерфейса, а потом согласно требованиям используемого канала передачи данных.
Согласно модели, на рисунке 10.1 канал передачи данных подвергается воздействию «дополнительного случайного шума». Весь шум в системе объединен в этой точке. Предполагается, что кодер принимает все символы без искажений, а декодер выполняет свою функцию без ошибок. Это некоторая идеализация, но для многих практических целей она близка к реальности.
Фаза декодирования также состоит из двух этапов: канал — стандарт, стандарт- приемник данных. В конце передачи данных передаются потребителю. И снова мы не рассматриваем вопрос, как потребитель трактует эти данные.
Как было отмечено ранее, система передачи данных, например, телефонных сообщений, радио, ТВ программ, представляет данные в виде набора чисел в регистрах вычислительной машины. Повторю снова, передача в пространстве не отличается от передачи во времени или сохранения информации. Есть ли у вас есть информация, которая потребуется через некоторое время, то ее необходимо закодировать и сохранить на источнике хранения данных. При необходимости информация декодируется. Если система кодирования и декодирования одинаковая, мы передаем данные через канал передачи без изменений.
Фундаментальная разница между представленной теорией и обычной теорией в физике — это предположение об отсутствии шума в источнике и приемнике. На самом деле, ошибки возникают в любом оборудовании. В квантовой механике шум возникает на любых этапах согласно принципу неопределённости, а не в качестве начального условия; в любом случае, понятие шума в теории информации не эквивалентно аналогичному понятию в квантовой механике.
Для определенности будем далее рассматривать бинарную форму представления данных в системе. Другие формы обрабатываются похожим образом, для упрощения не будем их рассматривать.
Начнем рассмотрение систем с закодированными символами переменной длины, как в классическом коде Морзе из точек и тире, в котором часто встречающиеся символы — короткие, а редкие — длинные. Такой подход позволяет достичь высокой эффективности кода, но стоит отметить, что код Морзе — тернарный, а не бинарный, так как в нём присутствует символ пробела между точками и тире. Если все символы в коде одинаковой длины, то такой код называется блочным.
Первое очевидное необходимое свойство кода — возможность однозначно декодировать сообщение при отсутствии шума, по крайней мере, это кажется желаемым свойством, хотя в некоторых ситуациях этим требованием можно пренебречь. Данные из канала передачи для приемника выглядят как поток символов из нулей и единичек.
Будем называть два смежных символа двойным расширением, три смежных символ тройным расширением, и в общем случае если мы пересылаем N символов приемник видит дополнения к базовому коду из N символов. Приемник, не зная значение N, должен разделить поток в транслируемые блоки. Или, другими словами, у приемника должна быть возможность выполнить декомпозицию потока единственным образом для того, чтобы восстановить исходное сообщение.
Рассмотрим алфавит из небольшого числа символов, обычно алфавиты намного больше. Алфавиты языков начинается от 16 до 36 символов, включая символы в верхнем и нижнем регистре, числа знаки, препинания. Например, в таблице ASCII 128 = 2^7 символов.
Рассмотрим специальный код, состоящий из 4 символов s1, s2, s3, s4
s1 = 0; s2 = 00; s3 = 01; s4 = 11.
Как приёмник должен трактовать следующее полученное выражение
0011?
Как s1s1s4 или как s2s4?
Вы не можете однозначно дать ответ на этот вопрос, этот код однозначно нет декодируется, следовательно, он неудовлетворительный. С другой стороны, код
s1 = 0; s2 = 10; s3 = 110; s4 = 111
декодирует сообщение уникальным способом. Возьмем произвольную строку и рассмотрим, как ее будет декодировать приемник. Вам необходимо построить дерево декодирования Согласно форме на рисунке 10.II. Строка
1101000010011011100010100110…
может быть разбита на блоки символов
110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110,…
согласно следующему правилу построения дерева декодирования:
Если вы находитесь в вершине дерева, то считываете следующий символ. Когда вы достигаете листа дерева, вы преобразовывает последовательность в символ и возвращайтесь назад на старт.
Причина существования такого дерева в том, что ни один символ не является префиксом другого, поэтому вы всегда знаете, когда необходимо вернуться в начало дерево декодирования.
Необходимо обратить внимание на следующее. Во-первых, декодирование строго поточный процесс, при котором каждый бит исследуется только однажды. Во-вторых, в протоколах обычно включаются символы, которые являются маркером окончания процесса декодирования и необходимы для обозначения конца сообщения.
Отказ от использования завершающего символа является частой ошибкой при дизайне кодов. Конечно же можно предусмотреть режим постоянного декодирования, в этом случае завершающая символ не нужен.
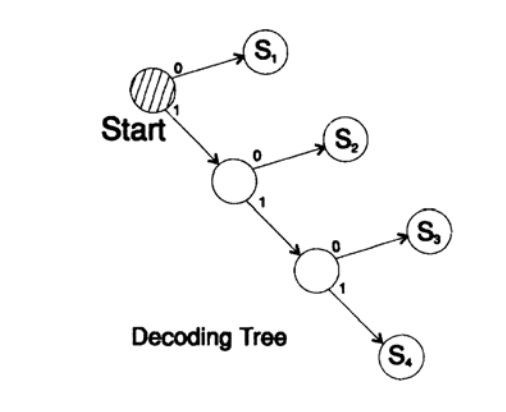
Рисунок 10.II
Следующий вопрос — это коды для поточного (мгновенного) декодирования. Рассмотрим код, который получается из предыдущего отображением символов
s1 = 0; s2 = 01; s3 = 011; s4 = 111.
Предположим мы получили последовательность 011111…111. Единственный способ, которым можно декодировать текст сообщения: группировать биты с конца по 3 в группе и выделять группы с ведущим нулем перед единичками, после этого можно декодировать. Такой код декодируемый единственным способом, но не мгновенным! Для декодирования необходимо дождаться окончания передачи! В практике такой подход нивелирует скорость декодирования (теорема Макмиллана), следовательно, необходимо поискать способы мгновенного декодирования.
Рассмотрим два способа кодирования одного и того же символа, Si:
s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,
Дерево декодирование этого способа представлено на рисунке 10.III.
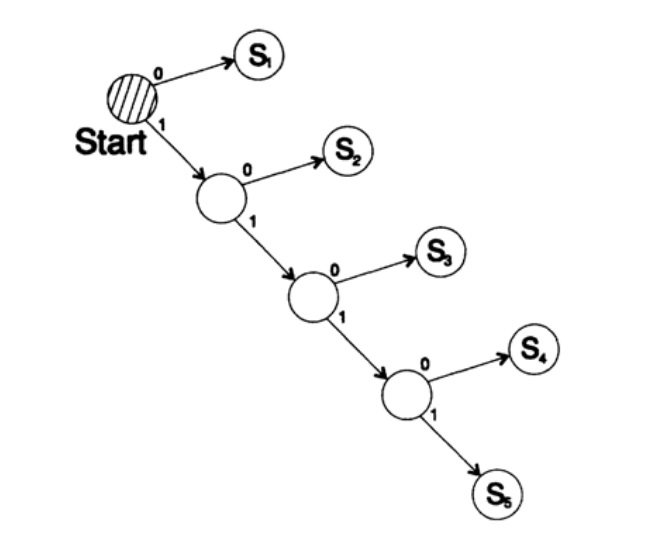
Рисунок 10.III
Второй способ
s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111,
Дерево декодирование это ухода представлены на рисунке 10.IV.
Наиболее очевидным способом измерения качество кода — это средняя длина для некоторого набора сообщений. Для этого необходимо вычислить длину кода каждого символа, помноженную на соответствующую вероятность появления pi. Таким образом получится длина всего кода. Формула средней длины L кода для алфавита из q символов выглядит следующим образом
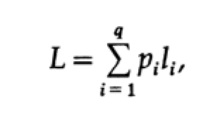
где pi — вероятность появления символа si, li — соответствующая длина закодированного символа. Для эффективного кода значение L должно быть как можно меньше. Если P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 и p5 = 1/16, тогда для кода #1 получаем значение длины кода
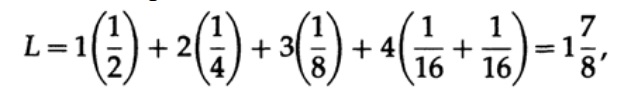
А для кода #2
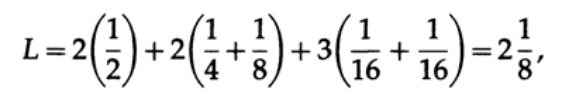
Полученные значения говорят о предпочтительности первого кода.
Если у всех слов в алфавите будет одинаковая вероятность возникновения, тогда более предпочтительным будет второй код. Например, при pi = 1/5 длина кода #1

а длина кода #2
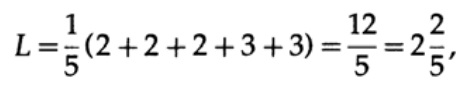
этот результат показывает предпочтительность 2 кода. Таким образом, при разработке «хорошего» кода необходимо учитывать вероятность возникновения символов.

Рисунок 10.IV

Рисунок 10.V
Рассмотрим неравенство Крафта, которое определяет предельное значение длины кода символа li. По базису 2 неравенство представляется в виде

Это неравенство говорит о том, что в алфавите не может быть слишком много коротких символов, в противном случае сумма будет довольно большой.
Для доказательства неравенства Крафта для любого быстрого уникального декодируемого кода построим дерево декодирования и применим метод математической индукции. Если у дерева есть один или два листа, как показано на рисунке 10.V, тогда без сомнения неравенство верно. Далее, в случае если у дерева есть более чем два листа, то разбиваем дерево длинный m на два поддерева. Согласно принципу индукции предполагаем, что неравенство верно для каждой ветви высотой m -1 или меньше. Согласно принципу индукции, применяя неравенство к каждой ветви. Обозначим длины кодов ветвей K’ и K”. При объединении двух ветвей дерева длина каждого возрастает на 1, следовательно, длина кода состоит из сумм K’/2 и K’’/2,
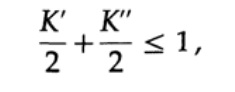
теорема доказана.
Рассмотрим доказательство теорема Макмиллана. Применим неравенство Крафта к непоточно декодируем кодам. Доказательство построено на том факте, что для любого числа K > 1 n-ая степень числа заведомо больше линейной функции от n, где n — довольно большое число. Возведем неравенство Крафта в n-ую степень и представим выражение в виде суммы
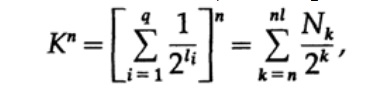
где Nk число символов длины k, суммирование начинаем с минимальной длины n-го представление символа и заканчиваем максимальной длины nl, где l — максимальная длина закодированного символа. Из требования уникального декодирования следует, что. Сумма представляется в виде

Если K > 1, тогда необходимо n установить довольно большим для того, чтобы неравенство стало ложным. Следовательно, k <= 1; теорема Макмиллана доказана.
Рассмотрим несколько примеров применения неравенство Крафта. Может ли существовать уникально декодируемый код с длинами 1, 3, 3, 3? Да, так как
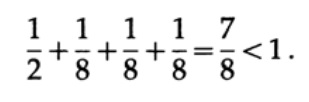
А что насчёт длин 1, 2, 2, 3? Рассчитаем согласно формуле
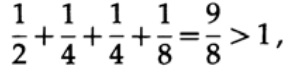
Неравенство нарушено! В этом коде слишком много коротких символов.
Точечные коды (comma codes) — это коды, которые состоят из символов 1, оканчивающиеся символом 0, за исключением последнего символа, состоящего из всех единичек. Одним из частных случаев служит код
s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5= 11111.
Для этого кода получаем выражение для неравенства Крафта

В этом случае достигаем равенство. Легко видеть, что для точечных кодов неравенство Крафта вырождается в равенство.
При построении кода необходимо обращать внимание на сумму Крафта. Если сумма Крафта начинает превышать 1, то это сигнал о необходимости включения символа другой длины для уменьшения средней длины кода.
Необходимо отметить, что неравенство Крафта говорит не о том, что этот код уникально декодируемый, а о том, что существует код с символами такой длины, которые уникальна декодируемый. Для построения уникальной декодируемого кода можно присвоить двоичным числом соответствующую длину в битах li. Например, для длин 2, 2, 3, 3, 4, 4, 4, 4 получаем неравенство Крафта
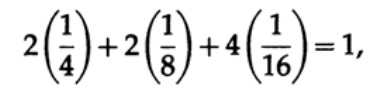
Следовательно, может существовать такой уникальный декодируемый поточной код.
s1 = 00; s2 = 01; s3 = 100; s4 = 101;
s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;
Хочу обратить внимание на то, что происходит на самом деле, когда мы обмениваемся идеями. Например, в этот момент времени я хочу передать идею из моей головы в вашу. Я произношу некоторые слова посредством которых, как я считаю, вы сможете понять (получить) эту идею.
Но когда чуть позже вы захотите передать эту идею своему другу, то почти наверняка произнесете совершенно другие слова. В действительности значение или смысл не заключены в рамках каких-то определённых слов. Я использовал одни слова, а вы можете использовать совершенно другие для передачи той же самой идеи. Таким образом, разные слова могут передавать одну и ту же информацию. Но, как только вы скажите своему собеседнику, что не понимаете сообщения, тогда как правило для передачи смысла собеседник подберёт другой набор слов, второй или даже третий. Таким образом, информация не заключена в наборе определенных слов. Как только вы получили те или иные слова, то производите большую работу при трансляции слов в идею, которую хочет до вас донести собеседник.
Мы учимся подбирать слова для того, чтобы подстроиться под собеседника. В некотором смысле мы выбираем слова согласовывая наши мысли и уровень шума в канале, хотя такое сравнение не точно отражает модель, который я использую для представления шумов в процессе декодирования. В больших организациях серьезной проблемой является неспособность собеседника слышать то, что сказано другим человеком. На высоких должностях сотрудники слышать то, «что хотят услышать». В некоторых случаях вам необходимо это помнить, когда вы будете продвигаться по карьерной лестнице. Представление информации в формальном виде является частичным отражением процессов из нашей жизни и нашло широкое применение далеко за границами формальных правил в компьютерных приложениях.
Продолжение следует…
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Содержание книги и переведенные главы
Предисловие
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) Перевод: Глава 1
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
- «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
- «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
- «Artificial Intelligence — Part I» (April 7, 1995) Глава 6. Искусственный интеллект — 1
- «Artificial Intelligence — Part II» (April 11, 1995) Глава 7. Искусственный интеллект — II
- «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
- «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) Глава 10. Теория кодирования — I
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995) Глава 11. Теория кодирования — II
- «Error-Correcting Codes» (April 21, 1995) Глава 12. Коды с коррекцией ошибок
- «Information Theory» (April 25, 1995) (пропал переводчик :((( )
- «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
- «Digital Filters, Part II» (April 28, 1995) Глава 15. Цифровые фильтры — 2
- «Digital Filters, Part III» (May 2, 1995) Глава 16. Цифровые фильтры — 3
- «Digital Filters, Part IV» (May 4, 1995) Глава 17. Цифровые фильтры — IV
- «Simulation, Part I» (May 5, 1995) Глава 18. Моделирование — I
- «Simulation, Part II» (May 9, 1995) Глава 19. Моделирование — II
- «Simulation, Part III» (May 11, 1995)
- «Fiber Optics» (May 12, 1995) Глава 21. Волоконная оптика
- «Computer Aided Instruction» (May 16, 1995) (пропал переводчик :((( )
- «Mathematics» (May 18, 1995) Глава 23. Математика
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) Глава 26. Эксперты
- «Unreliable Data» (May 26, 1995) Глава 27. Недостоверные данные
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
- «How Do We Know What We Know» (June 2, 1995) пропал переводчик :(((
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кодирование Хаффмана (часть 1 и 2)
| Редактировалось 10 янв 2018
Кодирование Хаффмана. Часть 1.
Вступление
Здравствуй, дорогой читатель! В данной статье будет рассмотрен один из способов сжатия данных. Этот способ является достаточно широко распространённым и заслуживает определённого внимания. Данный материал рассчитан по объёму на три статьи, первая из которых будет посвящена алгоритму сжатия, вторая – программной реализации алгоритма, а третья ― декомпрессии. Алгоритм сжатия будет написан на языке C++, алгоритм декомпрессии ― на языке Assembler.
Однако, перед тем, как приступить к самому алгоритму, следует включить в статью немного теории.
Немного теории
Компрессия (сжатие) ― способ уменьшения объёма данных с целью дальнейшей их передачи и хранения.
Декомпрессия ― это способ восстановления сжатых данных в исходные.
Компрессия и декомпрессия могут быть как без потери качества (когда передаваемая/хранимая информация в сжатом виде после декомпрессии абсолютно идентична исходной), так и с потерей качества (когда данные после декомпрессии отличаются от оригинальных). Например, текстовые документы, базы данных, программы могут быть сжаты только способом без потери качества, в то время как картинки, видеоролики и аудиофайлы сжимаются именно за счёт потери качества исходных данных (характерный пример алгоритмов ― JPEG, MPEG, ADPCM), при порой незаметной потере качества даже при сжатии 1:4 или 1:10.
Выделяются основные виды упаковки:
- Десятичная упаковка предназначена для упаковки символьных данных, состоящих только из чисел. Вместо используемых 8 бит под символ можно вполне рационально использовать всего лишь 4 бита для десятичных и шестнадцатеричных цифр, 3 бита для восьмеричных и так далее. При подобном подходе уже ощущается сжатие минимум 1:2.
- Относительное кодирование является кодированием с потерей качества. Оно основано на том, что последующий элемент данных отличается от предыдущего на величину, занимающую в памяти меньше места, чем сам элемент. Характерным примером является аудиосжатие ADPCM (Adaptive Differencial Pulse Code Modulation), широко применяемое в цифровой телефонии и позволяющее сжимать звуковые данные в соотношении 1:2 с практически незаметной потерей качества.
- Символьное подавление – способ сжатия информации, при котором длинные последовательности из идентичных данных заменяются более короткими.
- Статистическое кодирование основано на том, что не все элементы данных встречаются с одинаковой частотой (или вероятностью). При таком подходе коды выбираются так, чтобы наиболее часто встречающемуся элементу соответствовал код с наименьшей длиной, а наименее частому ― с наибольшей.
Кроме этого, коды подбираются таким образом, чтобы при декодировании можно было однозначно определить элемент исходных данных. При таком подходе возможно только бит-ориентированное кодирование, при котором выделяются разрешённые и запрещённые коды. Если при декодировании битовой последовательности код оказался запрещённым, то к нему необходимо добавить ещё один бит исходной последовательности и повторить операцию декодирования. Примерами такого кодирования являются алгоритмы Шеннона и Хаффмана, последний из которых мы и будем рассматривать.
Конкретнее об алгоритме
Как уже известно из предыдущего подраздела, алгоритм Хафмана основан на статистическом кодировании. Разберёмся поподробнее в его реализации.
Пусть имеется источник данных, который передаёт символы [math](a_1, a_2, …, a_n)[/math] с разной степенью вероятности, то есть каждому [math]a_i[/math] соответствует своя вероятность (или частота) [math]P_i(a_i)[/math], при чём существует хотя бы одна пара [math]a_i[/math] и [math]a_j[/math] ,[math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] не равны. Таким образом образуется набор частот [math]{P_1(a_1), P_2(a_2),…,P_n(a_n)}[/math], при чём [math]displaystyle sum_{i=1}^{n} P_i(a_i)=1[/math], так как передатчик не передаёт больше никаких символов кроме как [math]{a_1,a_2,…,a_n}[/math].
Наша задача ― подобрать такие кодовые символы [math]{b_1, b_2,…,b_n}[/math] с длинами [math]{L_1(b_1),L_2(b_2),…,L_n(b_n)}[/math], чтобы средняя длина кодового символа не превышала средней длины исходного символа. При этом нужно учитывать условие, что если [math]P_i(a_i)>P_j(a_j)[/math] и [math]ine j[/math], то [math]L_i(b_i)le L_j(b_j)[/math].
Хафман предложил строить дерево, в котором узлы с наибольшей вероятностью наименее удалены от корня. Отсюда и вытекает сам способ построения дерева:
1. Выбрать два символа [math]a_i[/math] и [math]a_j[/math], [math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] из всего списка [math]{P_1(a_1),P_2,…,P_n(a_n)}[/math] являются минимальными.
2. Свести ветки дерева от этих двух элементов в одну точку с вероятностью [math]P=P_i(a_i)+P_j(a_j)[/math], пометив одну ветку нулём, а другую ― единицей (по собственному усмотрению).
3. Повторить пункт 1 с учётом новой точки вместо [math]a_i[/math] и [math]a_j[/math], если количество получившихся точек больше единицы. В противном случае мы достигли корня дерева.
Теперь попробуем воспользоваться полученной теорией и закодировать информацию, передаваемую источником, на примере семи символов.
Разберём подробно первый цикл. На рисунке изображена таблица, в которой каждому символу [math]a_i[/math] соответствует своя вероятность (частота) [math]P_i(a_i)[/math]. Согласно пункту 1 мы выбираем два символа из таблицы с наименьшей вероятностью. В нашем случае это [math]a_1[/math] и [math]a_4[/math]. Согласно пункту 2 сводим ветки дерева от [math]a_1[/math] и [math]a_4[/math] в одну точку и помечаем ветку, ведущую к [math]a_1[/math], единицей, а ветку, ведущую к [math]a_4[/math],― нулём. Над новой точкой приписываем её вероятность (в данном случае ― 0.03) В дальнейшем действия повторяются уже с учётом новой точки и без учёта [math]a_1[/math] и [math]a_4[/math].
После многократного повторения изложенных действий выстраивается следующее дерево:
По построенному дереву можно определить значение кодов [math]{b_1,b_2,…,b_n}[/math], осуществляя спуск от корня к соответствующему элементу [math]a_i[/math], при этом приписывая к получаемой последовательности при прохождении каждой ветки ноль или единицу (в зависимости от того, как именуется конкретная ветка). Таким образом таблица кодов выглядит следующим образом:
i bi Li(bi) 1 011111 6 2 1 1 3 0110 4 4 011110 6 5 010 3 6 00 2 7 01110 5 Теперь попробуем закодировать последовательность из символов.
Пусть символу [math]a_i[/math] соответствует (в качестве примера) число [math]i[/math]. Пусть имеется последовательность 12672262. Нужно получить результирующий двоичный код.
Для кодирования можно использовать уже имеющуюся таблицу кодовых символов [math]b_i[/math] при учёте, что [math]b_i[/math] соответствует символу [math]a_i[/math]. В таком случае код для цифры 1 будет представлять собой последовательность 011111, для цифры 2 ― 1, а для цифры 6 ― 00. Таким образом, получаем следующий результат:
Данные 1 2 6 7 2 2 6 2 Длина кода Исходные 001 010 110 111 010 010 110 010 24 бит Кодированные 011111 1 00 01110 1 1 00 1 19 бит В результате кодирования мы выиграли 5 бит и записали последовательность 19 битами вместо 24.
Однако это не даёт полной оценки сжатия данных. Вернёмся к математике и оценим степень сжатия кода. Для этого понадобится энтропийная оценка.
Энтропия ― мера неопределённости ситуации (случайной величины) с конечным или с чётным числом исходов. Математически энтропия формулируется как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятых с обратным знаком:[math]H(X)=-displaystyle sum_{i=1}^{n}P_icdot log_d (P_i)[/math].Где [math]X[/math] ― дискретная случайная величина (в нашем случае ― кодовый символ), а [math]d[/math] ― произвольное основание, большее единицы. Выбор основания равносилен выбору определённой единицы измерения энтропии. Так как мы имеем дело с двоичными цифрами, то в качестве основания рационально выбрать [math]d=2[/math].
Таким образом, энтропию для нашего случая можно представить в виде:[math]H(b)=-displaystyle sum_{i=1}^{n}P_i(a_i)cdot log_2 (P_i(a_i))[/math].Энтропия обладает замечательным свойством: она равна минимальной допустимой средней длине кодового символа [math]overline{L_{min}}[/math] в битах. Сама же средняя длина кодового символа вычисляется по формуле
[math]overline{L(b)}=displaystyle sum_{i=1}^{n}P_i(a_i)cdot L_i(b_i)[/math].Подставляя значения в формулы [math]H(b)[/math] и [math]overline{L(b)}[/math], получаем следующий результат: [math]H(b)=2,048[/math], [math]overline{L(b)}=2,100[/math].
Величины [math]H(b)[/math] и [math]overline{L(b)}[/math] очень близки, что говорит о реальном выигрыше в выборе алгоритма. Теперь сравним среднюю длину исходного символа и среднюю длину кодового символа через отношение:[math]frac{overline{L_{src}}}{L(b)}=frac{3}{2,1}=1,429[/math].Таким образом, мы получили сжатие в соотношении 1:1,429, что очень неплохо.
И напоследок, решим последнюю задачу: дешифровка последовательности битов.
Пусть для нашей ситуации имеется последовательность битов:001101100001110001000111111Необходимо определить исходный код, то есть декодировать эту последовательность.
Конечно, в такой ситуации можно воспользоваться таблицей кодов, но это достаточно неудобно, так как длина кодовых символов непостоянна. Гораздо удобнее осуществить спуск по дереву (начиная с корня) по следующему правилу:
1. Исходная точка ― корень дерева.
2. Прочитать новый бит. Если он ноль, то пройти по ветке, помеченной нулём, в противном случае ― единицей.
3. Если точка, в которую мы попали, конечная, то мы определили кодовый символ, который следует записать и вернуться к пункту 1. В противном случае следует повторить пункт 2.
Рассмотрим пример декодирования первого символа. Мы находимся в точке с вероятностью 1,00 (корень дерева), считываем первый бит последовательности и отправляемся по ветке, помеченной нулём, в точку с вероятностью 0,60. Так как эта точка не является конечной в дереве, то считываем следующий бит, который тоже равен нулю, и отправляемся по ветке, помеченной нулём, в точку [math]a_6[/math], которая является конечной. Мы дешифровали символ ― это число 6. Записываем его и возвращаемся в исходное состояние (перемещаемся в корень).
Таким образом декодированная последовательность принимает вид.
Данные 001101100001110001000111111 Длина кода Кодированные 00 1 1 0110 00 01110 00 1 00 011111 1 27 бит Исходные 6 2 2 3 6 7 6 2 6 1 2 33 бит В данном случае выигрыш составил 6 бит при достаточно небольшой длине последовательности.
Вывод напрашивается сам собой: алгоритм прост. Однако следует сделать замечание: данный алгоритм хорош для сжатия текстовой информации (действительно, реально мы используем при набивке текста примерно 60 символов из доступных 256, то есть вероятность встретить иные символы близка к нулю), но достаточно плох для сжатия программ (так как в программе все символы практически равновероятны). Так что эффективность алгоритма очень сильно зависит от типа сжимаемых данных.
Постскриптум
В этой статье мы рассмотрели алгоритм кодирования по методу Хаффмана, который базируется на неравномерном кодировании. Он позволяет уменьшить размер передаваемых или хранимых данных. Алгоритм прост для понимания и может давать реальный выигрыш. Кроме этого, он обладает ещё одним замечательным свойством: возможность кодировать и декодировать информацию “на лету” при условии того, что вероятности кодовых слов правильно определены. Хотя существует модификация алгоритма, позволяющая изменять структуру дерева в реальном времени.
В следующей части статьи мы рассмотрим байт-ориентированное сжатие файлов с использованием алгоритма Хаффмана, реализованное на C++.
Кодирование Хаффмана. Часть 2
Вступление
В прошлой части мы рассмотрели алгоритм кодирования, описали его математическую модель, произвели кодирование и декодирование на конкретном примере, рассчитали среднюю длину кодового слова, а также определили коэффициент сжатия. Кроме этого, были сделаны выводы о преимуществах и недостатках данного алгоритма.
Однако, помимо этого неразрешёнными остались ещё два вопроса: реализация программы, сжимающей файл данных, и программы, распаковывающей сжатый файл. Первому вопросу и посвящена настоящая статья. Поэтому следует заняться проектированием.
Проектирование
Первым делом необходимо посчитать частоты вхождения символов в файл. Для этого опишем следующую структуру:
Эта структура будет описывать каждый символ из 256. ch ― сам ASCII-символ, freq ― количество вхождений символа в файл. Поле table ― указатель на структуру:
Как видно, TTable ― это описатель узла с разветвлением по нулю и единице. При помощи этих структур в дальнейшем и будет осуществляться построение дерева компрессии. Теперь объявим для каждого символа свою частоту и свой узел:
Попробуем разобраться, каким образом будет осуществляться построение дерева. На начальной стадии программа должна осуществить проход по всему файлу и подсчитать количество вхождений символов в него. Помимо этого, для каждого найденного символа программа должна создать описатель узла. После этого из созданных узлов с учётом частоты символов программа строит дерево, размещая узлы в определённом порядке и устанавливая между ними связи.
Построенное дерево хорошо для декодирования файла. Но для кодирования файла оно неудобно, потому что неизвестно, в каком направлении следует идти от корня, чтобы добраться до необходимого символа. Для этого удобнее построить таблицу преобразования символов в код. Поэтому определим ещё одну структуру:
Здесь opcode ― кодовая комбинация символа, а len – её длина (в битах). И объявим таблицу из 256 таких структур:
Зная кодируемый символ, можно определить его кодовое слово по таблице. Теперь перейдём непосредственно к подсчёту частот символов (и не только).
Подсчёт частот символов
В принципе, это действие не составляет труда. Достаточно открыть файл и подсчитать в нём число символов, заполнив соответствующие структуры. Посмотрим реализацию этого действия.
Для этого объявим глобальные дескрипторы файлов:in ― файл, из которого осуществляется чтение несжатых данных.
out ― файл, в который осуществляется запись сжатых данных.
assemb ― файл, в который будет сохранено дерево в удобном для распаковки виде. Так как распаковщик будет написан на ассемблере, то вполне рационально дерево сделать частью распаковщика, то есть представить его в виде инструкций на Ассемблере.
Первым делом необходимо проинициализировать все структуры нулевыми значениями:
После этого мы подсчитываем число вхождений символа в файл и размер файла (конечно, не самым идеальным способом, но в примере нужна наглядность):
Так как код неравномерный, то распаковщику будет проблематично узнать число считываемых символов. Поэтому в таблице распаковки необходимо зафиксировать его размер:
После этого все используемые символы смещаются в начало массива, а неиспользуемые затираются (путём перестановок).
И только после такой “сортировки” выделяется память под узлы (для некоторой экономии).
Таким образом, мы написали функцию первоначальной иницализации системы, или, если смотреть на алгоритм в первой части статьи, “записали используемые символы в столбик и приписали к ним вероятности”, а также для каждого символа создали “отправную точку” ― узел ― и проинициализировали её. В поля left и right записали нули. Таким образом, если узел будет в дереве последним, то это будет легко увидеть по left и right, равным нулю.
Создание дерева
Итак, в предыдущем разделе мы “записали используемые символы в столбик и приписали к ним вероятности”. На самом деле, мы приписали к ним не вероятности, а числители дроби (то есть количество вхождений символов в файл). Теперь надо построить дерево. Но для того, чтобы это сделать, необходимо найти минимальный элемент в списке. Для этого вводим функцию, в которую передаём два параметра ― количество элементов в списке и элемент, который следует исключить (потому что искать будем парами, и будет очень неприятно, если мы от функции дважды получим один и тот же элемент):
Поиск реализован несложно: сначала выбираем “минимальный” элемент массива. Если исключаемый элемент ― 0, то берём в качестве минимума первый элемент, в противном случае минимумом считаем нулевой. По мере прохождения по массиву сравниваем текущий элемент с “минимальным”, и если он окажется меньше, то его помечаем как минимальный.
Теперь, собственно говоря, сама функция построения дерева:
Таблица кодовых символов
Итак, дерево в памяти мы построили: попарно брали два узла, создавали новый узел, в который записывали на них указатели, после чего второй узел удаляли из списка, а вместо первого узла писали новый с разветвлением.
Теперь возникает ещё одна проблема: кодировать по дереву неудобно, потому что необходимо точно знать, по какому пути находится тот или иной символ. Однако проблема решается довольно просто: создаётся ещё одна таблица ― таблица кодовых символов ― в неё и записываются битовые комбинации всех используемых символов. Для этого достаточно однократно рекурсивно обойти дерево. Заодно, чтобы повторно его не обходить, можно в функцию обхода добавить генерацию ассемблерного файла для дальнейшего декодирования сжатых данных (см. раздел “Проектирование“).
Собственно, сама функция не сложна. Она должна приписывать к кодовой комбинации 0 или 1, если узел не конечный, в противном случае добавить кодовый символ в таблицу. Помимо всего этого, сгенерировать ассемблерный файл. Рассмотрим эту функцию:
Помимо всего прочего, после прохождения узла функция удаляет его (освобождает указатель). Теперь разберёмся, что за параметры передаются в функцию.
- tbl ― узел, который надо обойти.
- opcode ― текущее кодовое слово. Старший бит должен быть всегда свободен.
- len ― длина кодового слова.
В принципе, функция не сложнее “классического факториала” и не должна вызывать трудностей.
Битовый вывод
Вот мы и добрались до не самой приятной части нашего архиватора, а именно ― до вывода кодовых символов в файл. Проблема состоит в том, что кодовые символы имеют неравномерную длину и вывод приходится осуществлять побитовый. В этом поможет функция PutCode. Но для начала объявим две переменные ― счётчик битов в байте и выводимый байт:OutBits увеличивается на один при каждом выводе бита, OutBits==8 сигнализирует о том, что OutChar следует сохранить в файл.
Помимо этого, нужно организовать что-то вроде “fflush”, то есть после вывода последнего кодового слова OutChar не поместится в выходной файл, так как OutBits!=8. Отсюда появляется ещё одна небольшая функция:
Вызываем помощников
Все рассмотренные ранее функции не являются основными. Но с их помощью можно проиллюстрировать простой порядок действий:
1. Выписать все элементы в столбик и приписать вероятности.
2. Построить дерево по полученному столбику.
3. Записать кодовую таблицу символов.
4. По кодовой таблице закодировать исходные данные.
Собственно говоря, вот и функция, которая выполняет эти действия:
Мейн
Всё, все функции готовы. Осталось только реализовать функцию main. Необходимо определить, какие она должна получить аргументы. А всё очень просто ― имя исходного файла, имя закодированного файла, а также имя файла, в который будет помещена таблица. Лично я всю операцию по открытию/закрытию файлов решил возложить на main. И вот как это выглядит:
Постскриптум
Вот и эта статья подошла к своему логическому завершению. В принципе, здесь представлен вполне рабочий код. Однако стоит заметить, что этот код не всегда способен работать. Например, если частоты символов обладают следующей закономерностью: 0.5, 0.25, 0.125, 0.0625, то есть у каждого символа вероятность его появления обратнопропорциональна степени двойки. В таком случае максимальная длина символа составит 255 бит, что никак не поместится в переменную типа DWORD. Поэтому для таких особых случаев придётся немного поднапрячься и усложнить генерацию кодовой таблицы.
Да, чуть не забыл. Провёл бенчмарк, сжав эту статью. Получил отношение 1:1.41, что довольно-таки неплохо.
P.P.S.
Позволю себе немного пофилософствовать. Сначала я не знал C++ и говорил: “C++ это – язык программирования”. Потом, когда стал его изучать, я всячески его хвалил: “он может то, может это, а вот это – вообще класс, это супер язык”. Но помере набора опыта С++ стал для меня “просто языком программирования”. Почувствуйте разницу между этими тремя утверждениями.
Скачать исходный код к статье
SadKo
Владимир Садовников
- Регистрация:
- 4 июн 2007
- Публикаций:
- 8

Кодирование Хаффмана является
простым алгоритмом для построения кодов переменной длины, имеющих минимальную
среднюю длину. Этот весьма популярный алгоритм служит основой многих
компьютерных программ сжатия текстовой и графической информации. Некоторые из
них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве
одной из ступеней многоуровневого процесса сжатия. Метод Хаффмана [Huffman 52] производит идеальное сжатие
(то есть, сжимает данные до их энтропии), если вероятности символов точно равны
отрицательным степеням числа 2. Алгоритм начинает строить кодовое дерево снизу
вверх, затем скользит вниз по дереву, чтобы построить каждый индивидуальный код
справа налево (от самого младшего бита к самому старшему). Начиная с работ
Д.Хаффмана 1952 года, этот алгоритм являлся предметом многих исследований.
(Последнее утверждение из § 3.8.1 показывает, что наилучший код переменной
длины можно иногда получить без этого алгоритма.)
Алгоритм начинается составлением
списка символов алфавита в порядке убывания их вероятностей. Затем от корня
строится дерево, листьями которого служат эти символы. Это делается по шагам,
причем на каждом шаге выбираются два символа с наименьшими вероятностями, добавляются
наверх частичного дерева, удаляются из списка и заменяются вспомогательным
символом, представляющим эти два символа. Вспомогательному символу
приписывается вероятность, равная сумме вероятностей, выбранных на этом шаге
символов. Когда список сокращается до одного вспомогательного символа,
представляющего весь алфавит, дерево объявляется построенным. Завершается
алгоритм спуском по дереву и построением кодов всех символов.
Лучше всего проиллюстрировать
этот алгоритм на простом примере. Имеется пять символов с вероятностями,
заданными на рис. 1.3а.

Рис. 1.3. Коды Хаффмана.
Символы
объединяются в пары в следующем порядке:
1.![]()
объединяется с ![]() ,
,
и оба заменяются комбинированным символом ![]() с вероятностью 0.2;
с вероятностью 0.2;
2.
Осталось четыре символа, ![]() с вероятностью 0.4, а также
с вероятностью 0.4, а также ![]() и
и ![]() с вероятностями по 0.2.
с вероятностями по 0.2.
Произвольно выбираем ![]() и
и
![]() , объединяем
, объединяем
их и заменяем вспомогательным символом ![]() с вероятностью 0.4;
с вероятностью 0.4;
3.
Теперь имеется три символа ![]() и
и ![]() с вероятностями 0.4, 0.2 и 0.4,
с вероятностями 0.4, 0.2 и 0.4,
соответственно. Выбираем и объединяем символы ![]() и
и ![]() во вспомогательный символ
во вспомогательный символ ![]() с вероятностью 0.6;
с вероятностью 0.6;
4.
Наконец, объединяем два оставшихся символа ![]() и
и ![]() и заменяем на
и заменяем на ![]() с вероятностью 1.
с вероятностью 1.
Дерево построено. Оно изображено
на рис. 1.3а, «лежа на боку», с корнем справа и пятью листьями слева. Для
назначения кодов мы произвольно приписываем бит 1 верхней ветке и бит 0 нижней
ветке дерева для каждой пары. В результате получаем следующие коды: 0, 10, 111,
1101 и 1100. Распределение битов по краям – произвольное.
Средняя длина этого кода равна ![]() бит/символ. Очень
бит/символ. Очень
важно то, что кодов Хаффмана бывает много. Некоторые шаги алгоритма выбирались
произвольным образом, поскольку было больше символов с минимальной
вероятностью. На рис. 1.3b показано, как можно объединить
символы по-другому и получить иной код Хаффмана (11, 01, 00, 101 и 100).
Средняя длина равна ![]() бит/символ
бит/символ
как и у предыдущего кода.
Пример: Дано 8 символов А, В, С, D, Е, F, G и H с вероятностями 1/30, 1/30,
1/30, 2/30, 3/30, 5/30, 5/30 и 12/30. На рис. 1.4а,b,с изображены три дерева кодов Хаффмана высоты 5 и 6
для этого алфавита.

Рис. 1.4. Три дерева Хаффмана для
восьми символов.
Средняя
длина этих кодов (в битах на символ) равна
![]() ,
,
![]() ,
,
![]() .
.
Пример: На рис. 1.4d показано другое дерево высоты 4
для восьми символов из предыдущего примера. Следующий анализ показывает, что
соответствующий ему код переменной длины плохой, хотя его длина меньше 4.
(Анализ.)
После объединения символов А, В, С, D, Е, F и G остаются символы ABEF (с вероятностью 10/30), CDG (с вероятностью 8/30) и H (с вероятностью 12/30). Символы ABEF и CDG имеют наименьшую вероятность,
поэтому их необходимо было слить в один, но вместо этого были объединены
символы CDG и H. Полученное дерево не является
деревом Хаффмана.
Таким образом, некоторый произвол
в построении дерева позволяет получать разные коды Хаффмана с одинаковой
средней длиной. Напрашивается вопрос: «Какой код Хаффмана, построенный для
данного алфавита, является наилучшим?» Ответ будет простым, хотя и неочевидным:
лучшим будет код с наименьшей дисперсией.
Дисперсия показывает насколько
сильно отклоняются длины индивидуальных кодов от их средней величины (это
понятие разъясняется в любом учебнике по статистике). Дисперсия кода 1.3а равна
![]() , а для кода
, а для кода
1.3b ![]() .
.
Код 1.3b является более предпочтительным (это будет
объяснено ниже). Внимательный взгляд на деревья показывает, как выбрать одно,
нужное нам. На дереве рис. 1.3а символ ![]() сливается с символом
сливается с символом ![]() , в то время как на рис. 1.3b он сливается с
, в то время как на рис. 1.3b он сливается с ![]() . Правило будет такое:
. Правило будет такое:
когда на дереве имеется более двух узлов с наименьшей вероятностью, следует
объединять символы с наибольшей и наименьшей вероятностью; это сокращает общую
дисперсию кода.
Если кодер просто записывает
сжатый файл на диск, то дисперсия кода не имеет значения. Коды Хаффмана с малой
дисперсией более предпочтительны только в случае, если кодер будет передавать
этот сжатый файл по линиям связи. В этом случае, код с большой дисперсией заставляет
кодер генерировать биты с переменной скоростью. Обычно данные передаются по
каналам связи с постоянной скоростью, поэтому кодер будет использовать буфер.
Биты сжатого файла помещаются в буфер по мере их генерации и подаются в канал с
постоянной скоростью для передачи. Легко видеть, что код с нулевой дисперсией
будет подаваться в буфер с постоянной скоростью, поэтому понадобится короткий
буфер, а большая дисперсия кода потребует использование длинного буфера.
Следующее утверждение можно
иногда найти в литературе по сжатию информации: длина кода Хаффмана символа ![]() с вероятностью
с вероятностью ![]() всегда не превосходит
всегда не превосходит ![]() . На самом деле, не
. На самом деле, не
смотря на справедливость этого утверждения во многих примерах, в общем случае
оно не верно. Я весьма признателен Гаю Блелоку, который указал мне на это
обстоятельство и сообщил пример кода, приведенного в табл. 1.5. Во второй
строке этой таблицы стоит символ с кодом длины 3 бита, в то время как ![]() .
.
|
|
Код |
|
|
|
0.01 |
000 |
6.644 |
7 |
|
0.30 |
001 |
1.737 |
2 |
|
0.34 |
01 |
1.556 |
2 |
|
0.35 |
1 |
1.515 |
2 |
Табл. 1.5. Пример кода Хаффмана.
Длина кода символа ![]() , конечно, зависит от
, конечно, зависит от
его вероятности ![]() .
.
Однако она также неявно зависит от размера алфавита. В большом алфавите
вероятности символов малы, поэтому коды Хаффмана имеют большую длину. В
маленьком алфавите наблюдается обратная картина. Интуитивно это понятно,
поскольку для малого алфавита требуется всего несколько кодов, поэтому все они
коротки, а большому алфавиту необходимо много кодов и некоторые из них должны
быть длинными.

Рис. 1.6. Код Хаффмана для
английского алфавита.
На рис. 1.6 показан код Хаффмана
для всех 26 букв английского алфавита.
Случай алфавита, в котором
символы равновероятны, особенно интересен. На рис. 1.7 приведены коды Хаффмана
для алфавита с 5, 6, 7 и 8 равновероятными символами. Если размер алфавита ![]() является степенью 2,
является степенью 2,
то получаются просто коды фиксированной длины. В других случаях коды весьма
близки к кодам с фиксированной длиной. Это означает, что использование кодов
переменной длины не дает никаких преимуществ. В табл. 1.8 приведены коды, их
средние длины и дисперсии.

Рис. 1.7. Коды Хаффмана с равными
вероятностями.
Тот факт, что данные с
равновероятными символами не сжимаются методом Хаффмана может означать, что
строки таких символов являются совершенно случайными. Однако, есть примеры
строк, в которых все символы равновероятны, но не являются случайными, и их
можно сжимать. Хорошим примером является последовательность ![]() , в которой каждый
, в которой каждый
символ встречается длинными сериями. Такую строку можно сжать методом RLE, но не методом Хаффмана.
(Буквосочетание RLE означает «run-length encoding», т.е. «кодирование длин серий».
Этот простой метод сам по себе мало эффективен, но его можно использовать в
алгоритмах сжатия со многими этапами, см. [Salomon, 2000).)
Табл.
1.8. Коды Хаффмана для 5 8 символов.
|
|
|
|
|
|
|
|
|
|
|
Ср.длина |
Дисперсия |
|
5 |
0.200 |
111 |
110 |
101 |
100 |
0 |
2.6 |
0.64 |
|||
|
6 |
0.167 |
111 |
110 |
101 |
100 |
01 |
00 |
2.672 |
0.2227 |
||
|
7 |
0.143 |
111 |
110 |
101 |
100 |
011 |
010 |
00 |
2.86 |
0.1226 |
|
|
8 |
0.125 |
111 |
110 |
101 |
100 |
011 |
010 |
001 |
000 |
3 |
0 |
Заметим, что метод Хаффмана не
работает в случае двухсимвольного алфавита. В таком алфавите одному символу
придется присвоить код 0, а другому 1. Метод Хаффмана не может присвоить одному
символу код короче одного бита. Если исходные данные (источник) состоят из
индивидуальных битов, как в случае двухуровневого (монохромного) изображения,
то возможно представление нескольких бит (4 или 8) в виде одного символа нового
недвоичного алфавита (из 16 или 256 символов). Проблема при таком подходе
заключается в том, что исходные битовые данные могли иметь определенные
статистические корреляционные свойства, которые могли быть утеряны при
объединении битов в символы. При сканировании монохромного рисунка или
диаграммы по строкам пикселы будут чаще встречаться длинными
последовательностями одного цвета, а не быстрым чередованием черных и белых. В
итоге получится файл, начинающийся с 1 или 0 (с вероятностью 1/2). За нулем с
большой вероятностью следует нуль, а за единицей единица. На рис. 1.9 изображен
конечный автомат, иллюстрирующий эту ситуацию. Если биты объединять в группы,
скажем, по 8 разрядов, то биты внутри группы будут коррелированы, но сами
группы не будут иметь корреляцию с исходными пикселами. Если входной файл
содержит, например, две соседние группы 00011100 и 00001110, то они будут
кодироваться независимо, игнорируя корреляцию последних нулей первой группы и
начальных нулей второй. Выбор длинных групп улучшает положение, но увеличивает
число возможных групп, что влечет за собой увеличение памяти для хранения
таблицы кодов и удлиняет время создания этой таблицы. (Напомним, что если
группа длины ![]() увеличивается
увеличивается
до длины ![]() , то
, то
число групп растет экспоненциально с ![]() до
до ![]() ).
).

Рис. 1.9. Конечный автомат.
Более сложный подход к сжатию
изображений с помощью кодов Хаффмана основан на создании нескольких полных
множеств кодов Хаффмана. Например, если длина группы равна 8 бит, то
порождается несколько семейств кодов размера 256. Когда необходимо закодировать
символ ![]() ,
,
выбирается одно семейство кодов, и ![]() кодируется из этого семейства.
кодируется из этого семейства.
Давид Хаффман (1925-1999)
Давид начал свою научную карьеру
студентом в Массачусетсом технологическом институте (MIT), где построил
свои коды в начале пятидесятых годов прошлого века.
Он поступил на факультет MIT в 1953 году.
В 1967 году Хаффман перешел в университет Санта Круз на факультет
компьютерных наук. Он играл заметную роль в развитии академической программы
факультета и в подборе преподавателей, возглавляя его с 1970 по 1973 года.
Выйдя на пенсию в 1994 году, Давид Хаффман продолжил свою научную
деятельность в качестве заслуженного профессора в отставке, читая курсы по
теории информации и по анализу сигналов. Он умер в 1999 году в возрасте 74
лет.
Хаффман сделал важный вклад во многих
областях науки, включая теорию информации и теорию кодирования. Он много
занимался прикладными задачами, например, проектированием сигналов для
радаров, разработкой процедур для асинхронных цепей и другими
коммуникационными проблемами. Побочным результатом его работы по
математическим свойствам поверхностей «нулевой кривизны» стало развитие им
оригинальной техники свертывания из бумаги необычных скульптурных форм (Grafica 96).
Пример: Представим себе изображение из
8-и битовых пикселов, в котором половина пикселов равна 127, а другая половина
имеет значение 128. Проанализируем эффективность метода RLE для индивидуальных битовых
областей по сравнению с кодированием Хаффмана.
(Анализ.) Двоичная запись 127
равна 01111111, а 128 – 10000000. Половина пикселов поверхности будет нулем, а
вторая половина единицей. В самом плохом случае область будет походить на
шахматную доску, то есть, иметь много серий длины 1. В этом случае каждая серия
требует кода в 1 бит, что ведет к одному кодовому биту на пиксел на область,
или 8 кодовых битов на пиксел для всего изображения. Это приводит к полному
отсутствию сжатия. А коду Хаффмана для такого изображения понадобится всего два
кода (поскольку имеется всего два разных пиксела), и они могут быть длины 1.
Это приводит к одному кодовому биту на пиксел, то есть к восьмикратному сжатию.
Равномерное алфавитное двоичное кодирование. Байтовый код
В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное %%I(А) = log_2 N%%. Формировать признак конца знака не требуется, поэтому для определения длины кода можно воспользоваться формулой %%K(A,2) > log_2 N%%. Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при этом недопустимы сбои, например, пропуск (непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи или иными способами, о которых пойдет речь далее. С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.
Примером равномерного алфавитного кодирования является телеграфный код Бодо, пришедший на смену азбуке Морзе. Исходный алфавит должен содержать не более 32-х символов; тогда %%К(А,2) = log_2 32 = 5%%, т.е. каждый знак первичного алфавита содержит 5 бит информации и кодируется цепочкой из 5 двоичных знаков. Условие %%N ≤ 32%%, очевидно, выполняется для языков, основанных на латинском алфавите (%%T = 27 = 26 + «пробел»%%), однако в русском алфавите 34 буквы (с пробелом) – именно по этой причине пришлось «сжать» алфавит (как в коде Хаффмана) и объединить в один знак «е» и «ё», а также «ь» и «ъ», что видно из табл. 3.1. После такого сжатия %%N = 32%%, однако, не остается свободных кодов для знаков препинания, поэтому в телеграммах они отсутствуют или заменяются буквенными аббревиатурами; это не является заметным ограничением, поскольку, как указывалось выше, избыточность языка позволяет легко восстановить информационное содержание сообщения. Избыточность кода Бодо для русского языка %%Q(r,2) = 0,148%%, для английского %%Q(e,2) = 0,239%%.
Другим важным для нас примером использования равномерного алфавитного кодирования является представление символьной (знаковой) информации в компьютере. Чтобы определить длину кода, необходимо начать с установления количество знаков в первичном алфавите. Компьютерный алфавит должен включать:
- 26 х 2 = 52 букв латинского алфавита (с учетом прописных и строчных);
- 33 х 2 = 66 букв русского алфавита;
- цифры 0.. .9 – всего 10;
- знаки математических операций, знаки препинания, спецсимволы %%≈ 20%.
Получаем, что общее число символов %%N ≈ 148%%. Теперь можно оценить длину кодовой цепочки: %%K(c,2) ≥ log_2 148 ≥ 7,21%%. Поскольку длина кода выражается целым числом, очевидно, К(с,2) = 8. Именно такой способ кодирования принят в компьютерных системах: любому символу ставится в соответствие код из 8 двоичных разрядов (8 бит). Эта последовательность сохраняется и обрабатывается как единое целое (т.е. отсутствует доступ к отдельному биту) – по этой причине разрядность устройств компьютера, предназначенных для хранения или обработки информации, кратна 8. Совокупность восьми связанных бит получила название байт, а представление таким образом символов – байтовым кодированием.
Байт наряду с битом может использоваться как единица измерения количества информации в сообщении. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным. Пусть имеется некоторое сообщение (последовательность знаков); оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона (2.17)) дает %%I_{вер}%%, а объемная мера пусть равна %%I_{об}%%; соотношение между этими величинами вытекает из (2.7):
%%I_{вер} leqslant I_{об}%%;
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:
- 1 Кбайт = %%2^{10}%% байт = 1024 байт
- 1 Мбайт = %%2^{20}%% байт = 1024 Кбайт
- 1 Гбайт = %%2^{30}%% байт = 1024 Мбайт
- 1 Тбайт = %%2^{40}%% байт = 1024 Гбайт
Использование 8-битных цепочек позволяет закодировать %%2^8=256%% символов, что превышает оцененное выше %%N%% и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Однако недостаточно только условиться об определенной длине кода. Ясно, что способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьмибитных цепочек, очень много. По этой причине для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов. Подобное согласование осуществляется в форме стандартизации кодовых таблиц.
Первым таким международным стандартом, который применялся на больших вычислительных машинах, был EBCDIC (Extended Binary Coded Decimal Interchange Code) – «расширенная двоичная кодировка десятичного кода обмена». В персональных компьютерах и телекоммуникационных системах применяется международный байтовый код ASCII (American Standard Code for Information Interchange – «американский стандартный код обмена информацией»).
Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0). В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31), вырабатываемые при использовании клавиатуры. Ниже приведены некоторые ASC-коды:
| Клавиша | Двоичный код | Десятичный код |
|---|---|---|
| A(лат) | 01000001 | 65 |
| Z | 01011010 | 90 |
| [Esc] | 00011011 | 27 |
Вторая часть кодовой таблицы – она считается расширением основной – охватывает коды в интервале от 128 до 255 (первый бит всех кодов 1). Она используется для представления символов национальных алфавитов (например, русского), а также символов псевдографики. Для этой части также имеются стандарты, например, для символов русского языка это КОИ-8, КОИ-7 и др.
Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их лексикографическому порядку (т.е. порядку следования в алфавите) – это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.
В настоящее время появился и находит все более широкое применение еще один международный стандарт кодировки -Unicode. Его особенность в том, что в нем использовано 16-битное кодирование, т.е. для представления каждого символа отводится 2 байта. Такая длина кода обеспечивает включения в первичный алфавит 65536 знаков. Это, в свою очередь, позволяет создать и использовать единую для всех распространенных алфавитов кодовую таблицу.
