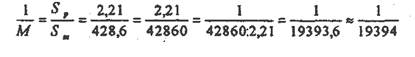Для измерения длины кривой линии имеются специальные приборы, которые называются Курвиметр. Чаще всего он используется для измерения на картах длины кривых линий (рек, дорог и так далее). Тогда он называется Картометр. На конце курвиметра имеется колесико. Это колесико проводят вдоль кривой линии. Колесико при этом вращается. Число оборотов колесика регистрируется счетчиком. Стрелка показывает длину измеренной линии.
Можно измерить длину кривой линии и циркулем. Но надо установить небольшой раствор циркуля, несколько мм. Длина такого шага зависит от степени извилистости измеряемой линии. Поворачивая циркуль последовательно вокруг иглы, движутся (шагают) по маршруту. Естественно, что длина кривой линии будет равна числу шагов циркуля, умноженному на шаг циркуля в масштабе карты. Плюс небольшой оставшийся остаток, который можно измерить обычной линейкой.
Если кривая линия не длинная, то можно взять узкую полоску бумаги, поставить ее на ребро и совместить с измеряемой линией. Затем по обычной линейке измерить длину бумажной полоски.
Можно измерить длину кривой линии и с помощью так называемого лонгометра. Он представляет собой сетку маленьких квадратов (как миллиметровая бумага), построенную (нарисованную) на прозрачном материале. Лучше, если вы нанесете на прозрачную пленку 2 сетки квадратов. Они пересекаются под углом 30°. Надо подсчитать число сторон квадратов , пересекаемых измеряемой линией, по сетке одного из цветов, а затем по сетке другого цвета. Берем среднее арифметическое по двум сеткам. Утроенное значение и даст нам длину измеряемой линии в масштабе карты.
Приветствую Вас, уважаемые Читатели! Согласитесь, найти точное значение наикратчайшего расстояния между двумя точками, да еще и на плоскости может каждый. Для этого придуманы всевозможные измерительные инструменты, а на координатной плоскости можно просто воспользоваться теоремой Пифагор . Но что, если речь идёт о поиске длины кривой линии? Как её найти?
Естественно, математикой уже давно найдено решение этой проблемы. Давайте придем к нему самостоятельно. Итак, поехали!
Найдем длину сегмента кривой, заданной уравнением y=f(x), разделив его на множество сегментов равной ширины и соединив получившиеся отрезки.
Теперь нужно найти каждый из отрезков, получился из-за нашей “нарезки”. Немного укрупнимся:
Мы использовали теорему Пифагора в первой строке, а во второй воспользовались теоремой Лагранжа о среднем значении (очень похожую на определение дифференциала).
Длина сегмента кривой АB при всё большем и большем количестве делений всё ближе и ближе становится к сумме длин отрезков, а значит с учетом непрерывности функции, задающей кривую, можно перейти от суммирования к интегрированию:
А теперь давайте отработаем простое применение этой формулы, вычислив длину окружности, заданной уравнением:
Пользуясь симметрией окружности, сначала вычислим длину четверти окружности, а затем умножим на 4:
- Спасибо за внимание! Надеюсь, материал понравился, ставьте “Нравится”!
- TELEGRAM и Вконтакте– там я публикую не только интересные статьи, но и математический юмор и многое другое.
Download Article
Download Article
You can measure the length of a vertical or horizontal line on a coordinate plane by simply counting coordinates; however, measuring the length of a diagonal line is trickier. You can use the Distance Formula to find the length of such a line. This formula is basically the Pythagorean Theorem, which you can see if you imagine the given line segment as the hypotenuse of a right triangle.[1]
By using a basic geometric formula, measuring lines on a coordinate path becomes a relatively easy task.
-
1
Set up the Distance Formula. The formula states that
, where
equals the distance of the line,
equal the coordinates of the first endpoint of the line segment, and
equal the coordinates of the second endpoint of the line segment.[2]
-
2
Find the coordinates of the line segment’s endpoints. These might already be given. If not, count along the x-axis and y-axis to find the coordinates.[3]
Advertisement
-
3
Plug the coordinates into the Distance Formula. Be careful to substitute the values for the correct variables. The two
coordinates should be inside the first set of parentheses, and the two
coordinates should be inside the second set of parentheses.[4]
Advertisement
-
1
Calculate the subtraction in parentheses. By using the order of operations, any calculations in parentheses must be completed first.[5]
-
2
Square the value in parentheses. The order of operations states that exponents should be addressed next.[6]
-
3
Add the numbers under the radical sign. You do this calculation as if you were working with whole numbers.[7]
-
4
Solve for
. To reach your final answer, find the square root of the sum under the radical sign.[8]
Advertisement
Add New Question
-
Question
What do we call points that are on same line?
Points on the same straight line are said to be “collinear” or “colinear.”
-
Question
How do I simplify the square root?
Look for a perfect square inside the radical sign, find its square root, and put that square root out in front of the radical sign, indicating that it’s to be multiplied by the radical. For example: √50 = √(2 x 25) = 5√2.
-
Question
The rise is 4 inches. The angle is 90 degrees from the height to the base. What is the slope?
To find the slope, you have to know the horizontal distance over which the rise occurs. The 90° angle is not relevant.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Remember the order of operations when calculating your answer. Subtract first, then square the differences, then add, and then find the square root.
-
Do not confuse this formula with others, like the Midpoint Formula, Slope Formula, Equation of a Line or Line Formula.
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
To use the distance formula to find the length of a line, start by finding the coordinates of the line segment’s endpoints. Then, plug the coordinates into the distance formula. Next, subtract the numbers in parenthesis and then square the differences. Once you’ve done that, just add the numbers that are under the radical sign and solve for d. To learn how to set up the distance formula, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 499,265 times.
Did this article help you?
Содержание
- Практическая работа №1 Решение задач на масштабы
- МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
- Практическая работа №1
Практическая работа №1 Решение задач на масштабы
Масштаб — это отношение длины линии на карте, плане (чертеже) Sp к длине горизонтального приложения соответствующей линии в натуре (на местности) Sm.
Численный масштаб — 1/ М, правильная дробь, у которой числитель равен 1, а знаменатель М показывает во сколько раз уменьшены линии местности по сравнению с планом.
Например, масштаб 1:10000 означает, что все линии местности уменьшены в 10000 раз, т.е. 1 см плана соответствует 10000 см на местности
или 1 см плана = 100 м на местности,
или 1 мм плана = 10 м на местности.
Следовательно, зная длину отрезка Sp плана по формуле Sm=Sp*M можно вычислить длину линии на местности или по формуле Sp= Sm:M определить длину отрезка на плане.
Например, длина линии на местности 252 м; масштаб плана 1:10000. Тогда длина линии на плане Бр=252м : 10000=0,0252м = 25,2мм.
И обратно, длина отрезка на плане равна 8,5 мм; масштаб плана 1:5000. Требуется определить длину линии местности. Она будет 8,5 мм * 5000 = 42,5м.
Задача №1 Вычислите длину линии на местности Sm, для данных, приведенных в таблице 1. Результаты запишите в соответствующую графу таблицы 1.
| Таблица 1. | |||||
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:10000 | 62,5 | 1:1000 | |||
| 1:25000 | 20,2 | 1:500 | |||
| 1:5000 | 12,5 | 1:2000 | |||
| 1:50000 | 6,2 | 1:5000 |
| Таблица 2. | |||||
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:2000 | 80,4 | 1:50000 | |||
| 1:5000 | 380,5 | 1:1000 | |||
| 1:10000 | 1:500 | ||||
| 1:25000 | 1:2000 |
Часто в геодезической практике приходится определять масштабы аэроснимков. Для этого измеряют длину отрезка на аэроснимке и длину горизонтального проложения этой линии на местности. Затем, используя определение масштаба, вычисляют масштаб.
Например: длина отрезка на аэроснимке 2.21 см.; длина горизонтального проложения этой линии на местности 428,6 м.
Тогда, согласно определению:
Задача №2Определите масштабы аэроснимков, по данным приведенным в таблице 3. результаты записать в соответствующую графу таблицы 3
| №п/п | Длина горизонтального приложения на местности м | Длина отрезка на аэроснимке | Отношение в соответствующих единицах | Масштаб аэроснимка |
| 625 м | 62,5 мм | 62,5 мм /625000мм | 1:10000 | |
| 525 м | 5,25 см | |||
| 125,5 м | 2,51 см | |||
| 62,2 м | 31,1 см |
Длины линий на местности, соответствующие 0,1 мм карты (плана) называется точностью масштаба — tm. Это величина, характеризующая точность определения длин линий по карте (плану). Например: точность масштаба 1:25000 равна 2,5 м.
Расчет можно вести следующим образом:
или to =0,1мм* 25000=2,5 м.
Задача №3
а) Определите точность масштабов:
б) Точность масштаба карты (плана) равна:
tm1=0,5м; t2=0,05M; t3=___ ___; t4=_______;
Определите масштаб карты (плана) .
1/М1=______; 1/М2=_______; 1 /МЗ=_______; 1/М4=_______;
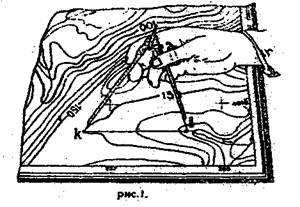
Задача №4 На карте масштаба 1:10000 (рис. 1) показан раствор измерителя, равный расстоянию между двумя точками карты KL. Используя приведенный ниже график линейного масштаба (рис.2), определите длины горизонтальных приложений линий местности для всех вариантов.
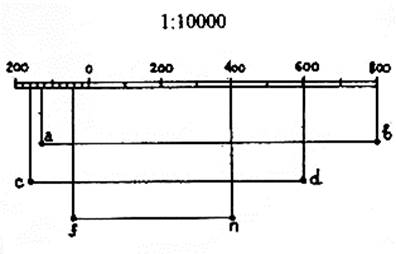
Задача №5 На графике поперечного масштаба (рис.3) с основанием равным 2 см., утолщенными линиями с номерами, обозначен раствор измерителя, равный расстоянию между двумя точками карты
Определите длины горизонтальных проложений линий местности для следующих вариантов:
| I вариант, масштаб 1:10000 | II вариант, масштаб 1:5000 |
| S1= | S1= |
| S2= | S2= |
| S5= | S5= |
| S= | S= |
| Ш вариант, масштаб 1:2000 S1= | IV вариант, масштаб 1: S1= |
| S2= | S2 = |
| S5= | S5 = |
| S= | S= |
Указание: в начале определите расстояния на местности (в соответствующем масштабе) для отрезков 0-2; а1в1; а2в2; аЗвЗ.
Задача №6 Постройте диаграмму масштаба 1:2000 на чертежной бумаге с основанием 2,5 см; число делений по основанию и по высоте принять равным 10 (n=m=10). Подпишите деления по основанию и высоте (через одно). Диаграмму приклеить, на оставленное ниже место.
Поделиться с друзьями:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.009 сек. —>
Источник
МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
РЕШЕНИЕ ГЕОДЕЗИЧЕСКИХ ЗАДАЧ
НА ТОПОГРАФИЧЕСКИХ ПЛАНАХ И КАРТАХ
Приведены основные геодезические задачи, решаемые на топографических картах и планах. Решение типовых задач дано с подробными пояснениями.
Вариантный подбор задач дает возможность проводить проверку знаний студентов. Ответы на большинство задач даны в конце методических указаний.
Предназначены для студентов специальностей СЖД, МТ, ВиВ, ПГС, ПТ и УПП всех форм обучения.
МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
При изображении участков земной поверхности на плане их размеры уменьшают в некоторое число раз. Отношение длины линии на плане к длине горизонтальной проекции соответствующей линии местности называют масштабом плана. Масштаб, выраженный дробью, у которой числитель равен единице, а знаменатель показывает, во сколько раз уменьшены горизонтальные расстояния местности при нанесении их на план, называется численным, например 
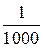
Чем больше знаменатель численного масштаба, тем масштаб мельче, чем знаменатель меньше, тем масштаб крупнее.
Масштаб 1 : 2 000 показывает, что 1 см на плане соответствует 20 м на местности (так как 2 000 см = 20 м).
С применением масштабов можно решать различные задачи.
Задача № 1. На плане масштаба 1 : 500 измерено расстояние а = = 56,5 мм. Определить длину d горизонтального проложения данной линии на местности.
Решение. Вычисление производится по формуле
где М – знаменатель численного масштаба.
Находим d = 56,5 · 500 = 28 250 мм = 28,25 м.
Задача № 2. Дано горизонтальное проложение линии на местности d = 214 м. Определить длину соответствующего отрезка на плане масштаба 1 : 2 000.
Решение. Используя формулу, приведенную в предыдущей задаче, получим:
а = d/М = 214/2 000 = 0,107 м = 10,7 см.
Задача № 3. Определить масштаб карты в пять раз крупнее масштаба 1 : 25 000.
Решение. Зная, что чем меньше знаменатель численного масштаба, тем масштаб крупнее, разделим знаменатель заданного масштаба на 5 и получим масштаб карты 1 : 5000.
Следующие задачи предлагается решить самостоятельно (ответы приведены в конце методических указаний).
Задача № 4. На плане масштаба 1 : 2 000 измерен отрезок длиной 4,3 см. Определить длину горизонтального проложения данного отрезка на местности.
Задача № 5. Какой отрезок следует отложить на плане масштаба 1 : 5 000, если горизонтальное расстояние на местности равно 850 м?
Задача № 6. Определить масштаб карты в два раза мельче масштаба 1 : 25 000.
При определении горизонтального проложения между двумя точками вначале необходимо измерить это расстояние на карте, а потом, используя численный масштаб карты, вычислить значение горизонтального проложения на местности. Чтобы не делать вычислений, связанных с использованием численного масштаба, под южной рамкой карты помещен графический (линейный) масштаб. В раствор циркуля берут с карты определяемое расстояние, прикладывают его к линейному масштабу и читают, какому расстоянию на местности оно соответствует. На рис. 1 изображен линейный масштаб для численного 1 : 10 000 и показаны расстояния 500 и 540 м.
Рис. 1. Определение расстояния по линейному масштабу
Задача № 7. Определить с помощью линейного масштаба на карте У-34-37-В-в-4 (см. приложение) расстояние между точкой с отметкой 151,8 м (квадрат 65×13) и точкой с отметкой 140,9 м (квадрат 65×13).
Для более точного измерения и откладывания расстояний на карте используют поперечный масштаб, который обычно выгравирован на металлических линейках, называемых масштабными.
Для построения поперечного масштаба на горизонтальной прямой откладывают несколько раз одинаковый отрезок, называемый основанием масштаба (рис. 2). Левое основание делят на 10 равных частей (малые деления). Из всех полученных точек восставляют перпендикуляры. На перпендикулярах также откладывают по 10 равных частей и через точки отложения проводят линии, параллельные основанию. Затем через деления левого основания проводят наклонные линии, как показано на рис. 2.
Рис. 2. Определение расстояний по поперечному масштабу
Из подобия треугольников BDE и Bde следует Вd/ВD = de/DE, или de = Bd · DE/BD. Но DE =АВ/10, поэтому Bd = ВD/10. Следовательно, de = АВ/100, т. е. наименьшее деление поперечного масштаба равно 0,01 основания. Эта величина называется предельной графической точностью поперечного масштаба.
Если основание масштаба равно 2 см, то поперечный масштаб носит название нормального поперечного масштаба.
Для определения расстояния между двумя точками на карте берут это расстояние в раствор циркуля-измерителя и переносят его на нижнюю линию поперечного масштаба. Если между иглами измерителя вмещается целое число оснований и малых делений, то отсчитывают расстояние. Если же левая игла измерителя попадает между двумя наклонными линиями малого деления, то измеритель перемещают вверх, параллельно основанию, пока левая игла не будет точно лежать на наклонной линии. Правая игла при этом должна располагаться на одной из вертикальных линий поперечного масштаба.
Задача № 8. Определить по схеме нормального поперечного масштаба (рис. 2) длину отрезка 1, измеренного на карте масштаба 1 : 10 000.
Решение. По численному масштабу карты определяем, что основанию (AB)поперечного масштаба 2 см соответствует расстояние на местности, равное 200 м. Левое основание разделено на 10 равных делений. Следовательно, малому делению (DE) соответствует расстояние в 20 м. Наименьшее деление поперечного масштаба (de),т. е. предельная графическая точность масштаба, составит 0,1 малого деления и равна 2 м. При определении длины отрезка 1 имеем: 2 · 200м + 6 · 20 м + 3 · 2 м = 526 м.
Задача № 9.Определить по нормальному поперечному масштабу на рис. 2 длину отрезка 2, измеренного на плане масштаба 1 : 2 000.
Решение. По численному масштабу плана определяем: основанию 2 см соответствует 40 м; малому делению – 4 м; наименьшему делению – 0,4 м. Искомая длина составит (см. рис. 2): вправо от B одно основание, то есть 40 м; влево от B три малых деления по 4 м, то есть 12 м; вверх по наклонной линии поднялись на 5 наименьших делений по 0,4 м каждое, чему соответствует 2 м. Получаем: 40 + 12 + 2 = 54 м.
Задача № 10. Определить по схеме нормального поперечного масштаба длины отрезков 1 и 3 для карты масштаба 1 : 25 000.
Задача № 11. Определить по схеме нормального поперечного масштаба длины отрезков 2 и 4 для плана масштаба 1 : 5 000.

Для измерения расстояния по извилистым дорогам, рекам и другим кривым линиям существуют специальные приборы, которые называют курвиметрами (рис. 3). В основании курвиметр имеет колесико, длина окружности которого известна. Колесиком прибора проводят по измеряемой линии. Вращение колесика передается на стрелку, указывающую на шкале циферблата измеренное расстояние. Для приближенного определения длины кривой линии (при отсутствии курвиметра) можно разбить ее на ряд отрезков, близких к прямым, и измерить ее как сумму прямых отрезков.
Рис. 3. Курвиметр
Задача № 13. Определить криволинейное расстояние по улучшенной грунтовой дороге (карта У-34-37-В-в-4) от населенного пункта Михалино до пересечения ее с шоссе (отметка 144,0 м, квадрат 65×14).
Источник
Практическая работа №1
на тему: «Масштабы топографических карт и планов»
ТЕМА: Масштабы топографических карт, планов и чертежей.
ЦЕЛЬ: Изучить масштаб и формы его выражения. Научиться измерять и откладывать длины отрезков на картах и планах. Получить навыки решения задач на масштабы.
В результате изучения темы студент должен:
- формы записи масштаба на карте, плане;
- определение масштаба;
- пользоваться графическим масштабом;
- выполнять метрические и угловые измерения на карте.
- Дать определение плана.
- Дать определение карты.
- Дать определение масштаба.
- Виды масштаба: численный, линейный и поперечный.
- Дать определение точности масштаба.
Задание 1. Вычислите длину линии на местности Sm, для данных, приведенных в таблице 1. Результаты запишите в соответствующую графу таблицы 1.
| Масштаб карты | Длина отрезка на карте (Sp), мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане Sp, мм | Длина линии на местности Sm, м |
| 1: 10000 | 62, 5 | 1: 1000 | |||
| 1: 25000 | 20, 2 | 1: 500 | |||
| 1: 5000 | 12, 5 | 1: 2000 | |||
| 1: 50000 | 6, 2 | 1: 5000 |
Задание 2.Вычислите длину линии на плане Sр для данных, приведенных в таблице 2. Результаты запишите в соответствующую графу таблицы 2.
| Масштаб карты | Длина отрезка на карте (Sp), мм | Длина линии на местности (Sm), м | Масштаб карты | Длина отрезка на плане (Sp), мм | Длина линии на местности (Sm), м |
| 1: 2000 | 80, 4 | 1: 50000 | |||
| 1: 5000 | 380, 5 | 1: 1000 | |||
| 1: 10000 | 1: 500 | ||||
| 1: 25000 | 1: 2000 |
Задание 3.Определите масштабы аэроснимков, по данным, приведенным в таблице 3. Результаты запишите в соответствующую графу таблицы 3.
| №п/п | Длина горизонтального проложения на местности (Sm), м | Длина отрезка на аэроснимке (Sp) | Отношение в соответствующих единицах | Масштаб аэроснимка |
| 625 м | 62, 5 мм | 62, 5 мм /625000мм | 1: 10000 | |
| 525 м | 5, 25 см | |||
| 125, 5 м | 2, 51 см | |||
| 62, 2 м | 31, 1 см |
Задание 4.Определите точность масштабов:
Задание 5. Используя приведенный ниже график линейного масштаба (рис.1), определите длины горизонтальных приложений линий местности для всех вариантов.
Рисунок 1 – Линейный масштаб
Задание 6. На графике поперечного масштаба с основанием равным 2 см утолщенными линиями с номерами, обозначен раствор измерителя, равный расстоянию между двумя точками карты. Определить длину линий для масштабов указанных ниже.
1 — масштаб 1: 10000 2 — масштаб 1: 5000
3 — масштаб 1: 2000 4 — масштаб 1:
Подпись студента_______ Подпись преподавателя____________
Источник
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:
В более общем случае, если у нас задана функция
в декартовых координатах и стоит задача найти длину дуги этой кривой между точками
и
,
нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение
означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.