Как найти длину кривой на поверхности

Как найти длину кривой на поверхности

Кривую 2 на поверхности с векторным уравнением можно задать следующим образом.

Пусть функции параметра t, Тогда векторная функция

определяет кривую, расположенную на поверхности

Это позволяет рассматривать соотношения

как уравнения кривой на поверхности

Пусть — гладкая кривая на поверхности Вычислим длину этой кривой между точками Так как векторное уравнение кривой то дифференциал дуги этой кривой можно выразить так:

откуда

или, более подробно,

Источник

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

1. Найти длину дуги на поверхности:
begin{equation*}
s=intlimits_{t_1}^{t_2}|vec{r’}(t)dt|=intlimits_{P_1}^{P_2}|dvec{r}(u,v)|=intlimits_{P_1}^{P_2}sqrt{I_1}.
end{equation*}
begin{equation*}
s=intlimits_{t_1}^{t_2}sqrt{Eleft(frac{du}{dt}right)^2+2Ffrac{du}{dt}frac{dv}{dt}+Gleft(frac{dv}{dt}right)^2}dt.
end{equation*}

2. Найти угол между двумя линиями на поверхности в точке их пересечения:

Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле:
begin{gather*}
mbox{cos},varphi = displaystylefrac{I_1(d,delta)}{sqrt{I_1(d)}cdotsqrt{I_1(delta)}} \
mbox{cos},varphi = displaystylefrac{E,du,delta u+F,(du,delta v+delta u,dv)+G,dv,delta v}{sqrt{E,du^2+2F,du,dv+G,dv^2}cdotsqrt{E,delta u^2+2F,delta u,delta v+G,delta v^2}}.
end{gather*}
Говорим, что кривая на поверхности $vec{r}=vec{r}(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec{r}=vec{r}_udu+vec{r}_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности:
begin{equation*}
S = iintlimits_{D}sqrt{EG-F^2}du,dv,
end{equation*}
где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2u,dv^2
end{equation*}
между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

begin{equation*}
E=1, ,, F=0,,, G=frac19,mbox{sh}^2u.
end{equation*}
begin{equation*}
v=3u ,, Rightarrow ,,dv=3du.
end{equation*}
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2ucdot9,du^2=(1+mbox{sh}^2u)du^2=mbox{ch}^2u,du^2.
end{equation*}
begin{equation*}
s=left|intlimits_{u_1}^{u_2} mbox{ch},u,duright| = |mbox{sh},u_2-mbox{sh},u_1|.
end{equation*}

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии
$$ u+v=a, ,, u-v=a,$$
лежащие на поверхности:
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=au.
end{equation*}

Решение задачи 2

Первая квадратичная форма данной поверхности:
begin{equation*}
I_1=(1+a^2),du^2+u^2,dv^2.
end{equation*}

Данные линии пересекаются в точке:
begin{equation*}
left{
begin{aligned}
u+v&=a,\
u-v&=a.
end{aligned}
right. quad Rightarrow quad P(u=a,v=0).
end{equation*}

Направления данных линий:
begin{equation*}
du+dv=0, ,, delta u-delta v=0,, Rightarrow
end{equation*}
begin{equation*}
du = -dv, ,, delta u = delta v.
end{equation*}

Подставляем всё в формулу:
begin{gather*}
mbox{cos},varphi = displaystylefrac{(1+a^2),du,delta u + u^2,dv,delta v}{sqrt{(1+a^2),du^2+u^2,dv^2}cdotsqrt{(1+a^2),delta u^2+u^2,delta v^2}} = \
= left( dv = -du, ,, delta v = delta u right) = \
= displaystylefrac{(1+a^2- u^2),du,delta u}{sqrt{(1+a^2+u^2)^2,du,delta u}}= frac{1+a^2-u^2}{1+a^2+u^2}=\
= left(P(u=a,v=0)right) = \
= frac{1}{1+2a^2}.
end{gather*}

Задача 3

Дана поверхность:
$$z=axy.$$
Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$.
Запишем коэффициенты первой квадратичной формы:
begin{align*}
&E=1+(z_x)^2=1+a^2y^2,\
&F=z_xz_y=a^2xy, \
&G=1+(z_y)^2=1+a^2x^2.
end{align*}

Направления координатных линий:
begin{align*}
&x=x_0 ,, Rightarrow dx=0,\
&y=y_0 ,, Rightarrow delta y=0.
end{align*}

Угол между линиями $x=x_0$, $y=y_0$ в точке $(x_0,y_0)$:
begin{align*}
&mbox{cos}, varphi = displaystylefrac{E,dx,delta x + F(dxdelta y+delta xdy)+Gdydelta y}{sqrt{Edx^2+2Fdxdy+Gdy^2}cdotsqrt{Edelta x^2+2Fdelta xdelta y+Gdelta y^2}}=\
&= displaystylefrac{Fdelta xdy}{sqrt{Gdy^2}cdotsqrt{Edelta x^2}}=displaystylefrac{(a^2x_0y_0)delta xdy}{sqrt{(1+a^2x_0^2)dy^2}cdotsqrt{(1+a^2y_0^2)delta x^2}}=\
& = displaystylefrac{a^2x_0y_0}{sqrt{(1+a^2x_0^2) }cdotsqrt{(1+a^2y_0^2) }}.
end{align*}

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

begin{equation*}
mbox{cos}, varphi = displaystylefrac{F}{sqrt{EG}}.
end{equation*}

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

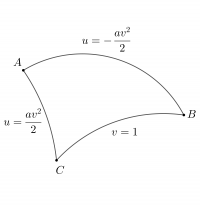
Задача 5 (Феденко 683)

Найти периметр и внутренние углы криволинейного треугольника
$$ u=pm av^2/2,,, v=1,$$
расположенного на поверхности
$$I_1=du^2+(u^2+a^2)dv^2.$$


Вершины треугольника:
begin{align*}
&A(u=0,, v=0),\
&B(u=-frac{a}{2},, v=1), \
&C(u=frac{a}{2},, v=1).
end{align*}

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника:
begin{align*}
&s_1 = |BC| = a,\
&s_2 = |AC| = frac76 a,\
&s_3 = |BC| = frac76 a,\
&P_{triangle ABC}=s_1+s_2+s_3=frac{10}{3}a.
end{align*}
begin{align*}
&mbox{cos},A = 1, ,, mbox{cos},B=mbox{cos},C=frac23.
end{align*}

Источник

Вопросы к экзамену по векторному и
тензорному анализу

2. Формулы Френе для плоской кривой

3. Кривизна кривой. Длина кривой

В дифференциальной геометрии, кривизна́
— собирательное название ряда
количественных характеристик (скалярных,
векторных, тензорных), описывающих
отклонение того или иного геометрического
«объекта» (кривой, поверхности, риманова
пространства и т. д.) от соответствующих
«плоских» объектов (прямая, плоскость,
евклидово пространство и т. д.).

Длина кривой (или, что то же, длина дуги
кривой) в метрическом пространстве —
числовая характеристика протяжённости
этой кривой.

Для евклидова пространства длина отрезка
кривой определяется как точная верхняя
грань длин вписанных в кривую ломаных.

Пусть непрерывная кривая γ задана
параметрически:

(1)

Где

Рассмотрим всевозможные разбиения
интервала значений параметра [a,b] на m
отрезков:

Соединив точки кривой

отрезками прямых, мы получим ломаную
линию. Тогда длина отрезка кривой
определяется как точная верхняя грань
суммарных длин всех таких ломаных.

Всякая непрерывная кривая имеет длину,
конечную или бесконечную. Если все
функции в (1) являются функциями
ограниченной вариации, то длина кривой
существует и конечна. В математическом
анализе выводится формула для вычисления
длины s отрезка кривой, заданной
уравнениями (1), при условии, что все три
функции непрерывно дифференцируемы:

4. Простые поверхности в евклидовом пространстве

Поверхности определяется как множество
точек, координаты которых удовлетворяют
определённому виду уравнений:

Если функция F(x,y,z)
непрерывна в некоторой точке и имеет в
ней непрерывные частные производные,
по крайней мере одна из которых не
обращается в нуль, то в окрестности этой
точки поверхность, заданная уравнением
(1), будет правильной поверхностью.

Помимо указанного выше неявного способа
задания поверхность может быть определена
явно, если одну из переменных, например
z, можно выразить через остальные:

Также существует параметрический способ
задания. В этом случае поверхность
определяется системой уравнений:

5. Касательная плоскость

Пусть имеется поверхность, заданная
уравнением F(x,y,z)=0.
Плоскость, в которой расположены все
касательные прямые к линиям на поверхности,
проходящим через данную точку

называется касательной плоскостью к
поверхности в точке M0

Если поверхность задана уравнением
F(x,y,z)=0
то уравнение касательной плоскости к
этой поверхности в точке М0:

Уравнение нормали в этой точке:

6. Длина кривой, заданной на поверхности

7. Первая квадратичная форма поверхности

Первая квадратичная форма или метрический
тензор поверхности ― квадратичная
форма от дифференциалов координат на
поверхности, которая определяет
внутреннюю геометрию поверхности в
окрестности данной точки. Знание первой
квадратичной формы достаточно для
вычисления длин дуг, углов между кривыми,
площади областей на поверхности.

Пусть поверхность задана уравнением

r = r(u,v),

где u и v ― внутренние координаты на
поверхности;

dr = rudu + rvdv

― дифференциал радиус-вектора r вдоль
выбранного направления смещения из
точки M в бесконечно близкую точку M’.
Квадрат главной липшицевой части
приращения длины | MM’ | выражается
квадратом дифференциала dr:

и называется первой основной квадратичной
формой поверхности. Коэффициенты первой
квадратичной формы обычно обозначают
через

или в тензорных символах

dr2
= g1,1du2 + 2g1,2dudv + g2,2dv2.

Тензор gi,j называется основным, или
метрическим, тензором поверхности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Приближение длины дуги эллипса с помощью ломаных

Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).

Определение[править | править код]

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.

Например, пусть непрерывная кривая gamma в трёхмерном пространстве задана параметрически:

x=x(t),quad y=y(t),quad z=z(t) (1)

Приближение кривой ломаными

где {displaystyle aleqslant tleqslant b}, все три функции непрерывны и нет кратных точек, то есть разным значениям t соответствуют разные точки кривой. Построим всевозможные разбиения параметрического интервала [a,b] на m отрезков: {displaystyle a=t_{0}<t_{1}<dots <t_{m}=b}. Соединение точек кривой {displaystyle gamma (t_{0}),dots ,gamma (t_{m})} отрезками прямых даёт ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных[2].

Длина дуги циклоиды (s) в зависимости от её параметра (θ)

Связанные определения[править | править код]

  • Всякая кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая. Снежинка Коха — классический пример ограниченной, но неспрямляемой кривой; более того, любая, сколь угодно малая её дуга неспрямляема[3].
  • Параметризация кривой длиной её дуги называется естественной.
  • Кривая есть частный случай функции из отрезка в пространство. Вариация функции, определяемая в математическом анализе, является обобщением длины кривой (см. ниже).

Свойства[править | править код]

  • Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна.
  • В математическом анализе выводится формула для вычисления длины s отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:
s=int limits _{a}^{b}{sqrt {{x'}^{2}(t)+{y'}^{2}(t)+{z'}^{2}(t)}},dt (2)
Формула подразумевает, что aleqslant b и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.
В n-мерном случае вместо (2) имеем аналогичную формулу:

s=int limits _{a}^{b}{sqrt {sum limits _{{k=1}}^{n}{f'_{k}}^{2}(t)}},dt.
{displaystyle s=int limits _{a}^{b}{sqrt {1+(f'(x))^{2}}},dx.}
В полярных координатах (r,varphi ):

s=int limits _{a}^{b}{sqrt {r^{2}+left({frac {dr}{dvarphi }}right)^{2}}},dvarphi .
  • Формула Крофтона позволяет связать длину кривой на плоскости и интеграл числа её пересечений с прямыми по естественной мере на пространстве прямых.

История[править | править код]

Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»[4][5].

Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина арки циклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.

Вариации и обобщения[править | править код]

Риманово пространство[править | править код]

В n-мерном римановом пространстве с координатами x^{1}cdots x^{n} кривая задаётся параметрическими уравнениями:

x^{i}=x^{i}(t)qquad qquad , ((3))

Длина кривой в римановом пространстве задаётся формулой:

s=int limits _{a}^{b}{sqrt {g_{{ij}}{dx^{i} over dt}{dx^{j} over dt}}},dt,

где : g_{ij} — метрический тензор.
Пример: кривая на поверхности в mathbb {R} ^{3}.

Общее метрическое пространство[править | править код]

В более общем случае произвольного метрического пространства (X,rho) длиной S кривой называется вариация задающего кривую отображения, то есть длина кривой gamma :[a,b]to X определяется согласно формуле:

s=sup sum limits _{{k=0}}^{m}rho (gamma (x_{{k+1}}),gamma (x_{k})),

где верхняя грань берётся, как и ранее, по всем разбиениям a=x_{0}<x_{1}<dots <x_{m}=b отрезка [a,b].

См. также[править | править код]

  • Дифференциальная геометрия кривых
  • Объём
  • Определённый интеграл
  • Площадь
  • Дуга окружности
  • Кривая Пеано

Примечания[править | править код]

  1. ↑ Длина // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
  2. ↑ Шибинский, 2007, с. 199.
  3. ↑ Шибинский, 2007, с. 201—202.
  4. ↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — С. 49. — 297 с. — (Классики естествознания).
  5. ↑ Оригинал цитаты на французском языке: «la proportion qui est entre les droites et les courbes n’étant pas connue, et même, je crois, ne le pouvant être par les hommes», см. Descartes, René. Discours de la méthode…. — 1637. — С. 340.

Литература[править | править код]

  • Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
  • Мерзон Г. А., Ященко И. В. Длина, площадь, объем. — МЦНМО, 2011. — ISBN 9785940577409.
  • Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966.
  • Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — 543 с. — ISBN 978-5-06-005774-4.
Источник

Добавить комментарий