Как найти и чему будет равна длина окружности
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Определение окружности
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Чтобы посчитать периметр круга, необходимо знать его диаметр (D) или радиус (R), который равняется D, деленному на 2.
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
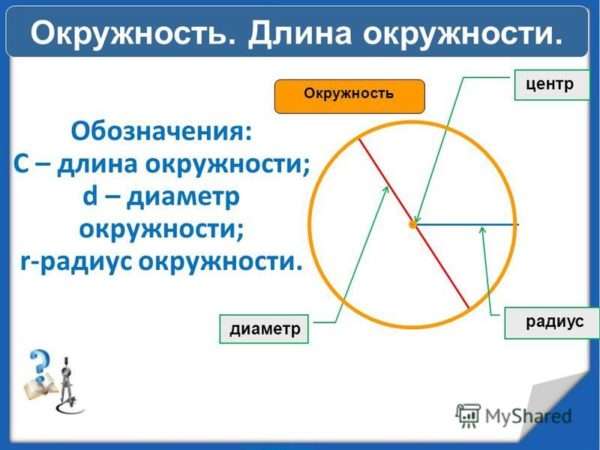Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана площадь круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR,
- через диаметр – L = πD,
- через площадь круга – L = 2√(Sπ).
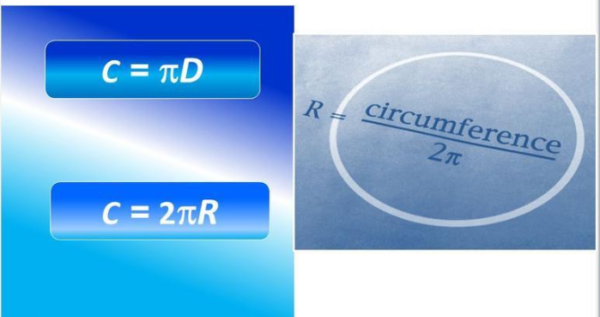Формулы
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Это интересно! Урок геометрии: как найти по формуле периметр треугольника
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг радиус, диаметр, длина окружности
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Длина окружности. Площадь круга (Вольфсон Г.И.)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке вы вспомните, что такое окружность и круг, а также некоторые их элементы. Кроме того, вы познакомитесь с числом и двумя новыми формулами: формулой длины окружности и формулой площади круга, научитесь применять их при решении задач.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Точность и округление»
[spoiler title=”источники:”]
http://poschitat.online/dlina-okruzhnosti
http://interneturok.ru/lesson/matematika/6-klass/otnosheniya-i-proporcii/dlina-okruzhnosti-ploschad-kruga
[/spoiler]
Содержание:
- § 1 История измерения длины окружности
- § 2 Формула длины окружности
§ 1 История измерения длины окружности
В этом уроке познакомимся с формулой длины окружности.
Одним из великих изобретений человечества является колесо. Историки утверждают, что колесо появилось еще в V веке до нашей эры. Сначала оно было глиняным, затем стало деревянным, а потом у колеса появились железные спицы и ободок.
Математической моделью колеса является окружность, поэтому геометрия колеса основана на геометрии окружности.
Окружность – это геометрическая фигура на плоскости, все точки которой равноудалены от ее центра. Вспомним, отрезок соединяющий центр окружности с любой точкой, лежащей на окружности, называется радиусом. Отрезок, соединящий две точки окружности и проходящий через ее центр – это диаметр.
Чтобы у телеги все четыре колеса были одинаковыми, требовалось измерять их диаметр или радиус. Окружности с одинаковыми диаметрами или радиусами при наложении совпадают.
Деревянные колеса быстро стирались, и тогда придумали обивать их железным ободком. Но как узнать длину железной полоски, которая станет ободком? Для этого нужно измерить длину окружности колеса. Можно взять веревочку, приложить ее по внешней стороне колеса, потом измерить длину веревки, вот и получится длина окружности.
Сравнивая длину окружности колеса и его диаметр, заметили, что соотношение данных измерений всегда приблизительно одинаковое.
Сначала считали, что длина окружности в 3 раза больше ее диаметра.
Математики Древней Греции стали обозначать соотношение длины окружности и ее диаметра буквой.
Было доказано, что число, обозначаемое этой буквой, относится к числам, точное значение которых невозможно записать в виде обыкновенной или десятичной дроби.
Необычность этого числа в том, что его нет ни среди целых, ни среди дробных чисел. Поэтому в математике его округляют.
Например, округленное число пи до разряда стомиллиардных: 3,14159265359.
Нам для решения задач достаточно округлить это число до сотых, т.е.
А на компьютере для более точных расчетов можно вычислить значение числа πи практически с любой точностью.
§ 2 Формула длины окружности
Выяснив, что соотношение длины окружности и ее диаметра равно числу π, можно найти длину окружности колеса.
Для этого нужно найти произведение диаметра окружности и числа π.
Обозначив длину окружности буквой С, а диаметр – буквой D, запишем формулу: C = πD
Часто в задачах даны размеры радиуса, а не диаметра.
Вспомним диаметр – это удвоенный радиус.
Тогда длину окружности можно найти по формуле C = 2πR, где R – радиус окружности.
Перейдем к практической части.
Дана окружность, диаметр которой равен 6,3 см.
Найдите длину этой окружности.
Выпишем данные: D = 6.3 см, π≈3,14, нужно найти С.
Подставим данные в формулу C = πD, получим С = π∙6,3; π≈3,14.
Значит С = 3,14 ∙ 6,3 = 19,782 см.
Итак, на этом уроке Вы познакомились с формулой длины окружности и научились ее применять при решении задач.
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина. Мнемозина. 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для общеобразовательных учреждений/Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др./ под редакцией Г.В. Дорофеева, И.Ф. Шарыгина; Рос.акад.наук, Рос.акад.образования, М.: Просвещение, 2010.
- Математика. 6 класс: учеб. для общеобразоват. учреждений/Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
- Математика. 6 кл.: учебник/Г.К. Муравин, О.В. Муравина. – М.: Дрофа, 2014.
Использованные изображения:
-
Log in
-
Join
Watch in our app
Open in app
Видеоурок как найти длину окружности
Длина окружности. Математика 6 класс.
Математика 6 Окружность Длина окружности
