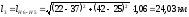На расстоянии, равном λ/4 от этой точки, ситуация обратная, т. е. напряжение равно нулю, а ток максимален. Это означает, что в этой точке сопротивление $Z_x=frac=frac<0>=0$. Введение короткозамыкателя в этой точке не приведет к изменению распределения тока и напряжения в линии. Распределение тока и напряжения вдоль разомкнутой на конце линяя не изменится при укорочении или удлинении линия на nλ/2 .
В общем случае сопротивление в точке питания А длинной линии А—В зависит как от длины линии, так и от характера нагрузки в точке В . В случае, когда длина линии равна $l=nfrac<lambda><2>$, сопротивление в точке А равно сопротивлению в точке В , т. е. Z 1 = Z 2 .
В случае, когда длина линии $l=frac<lambda(2n+1)><4>$, происходит трансформация сопротивления. Так, например, если Z2=∞ (линия разомкнута), то входное сопротивление Z1=0, и наоборот, если Z2=0 (линия коротко замкнута), то Z1=∞.
Еще раз подчеркнем, что входное сопротивление линии зависит как от характера нагрузки, так и от электрической длины линии, которая является функцией длины волны Так как с этими закономерностями приходится сталкиваться достаточно часто при проектировании линий питания и элементов фазирования антенных систем, авторы рекомендуют их тщательно изучить и запомнить. В какой-то мере читателю в этом помогут рис. 2.35 и 2.36, на которых представлен характер изменения входного сопротивления разомкнутой и коротко замкнутой линий при изменении их длины.
Входное сопротивление линии
В общем случае нагрузка линии может носить комплексный характер, т. е. $Z_2=R_2+iX_2$ . Тогда входное сопротивление такой линии согласно [2] $$beginZ_1=Z_0frac>>endtag<2.82>$$
Формула (2.82) справедлива для линий без потерь.
Введем теперь отношение волнового сопротивления линии к сопротивлению нагрузки Z 2 и обозначим эту величину через $$begins=fracendtag<2.83а>$$
Формулой (2.83а) следует пользоваться, если $$|Z_0|geqslant<|Z_2|>$$ Если же $$|Z_2geqslant<|Z_0|>$$ , то тогда $$begins=fracendlabel<2.83б>$$
Теперь, используя введенное соотношение, формулу (2.82) можно записать в виде $$beginZ_1=Z_0,frac<cos+i,ssin>+isin>endtag<2.84>$$
Эти трудные на первый взгляд формулы достаточно просты для конкретных расчетов. Применим их на конкретном примере.
Пример. На рис. 2.37 приведена линия длиной l=2 м, имеющая волновое сопротивление Z0=300 Ом. Эта линия нагружена на последовательно включенные емкость С=20 пФ и сопротивление R2=200 Ом. Рассчитаем входное сопротивление Z1 этой линии для волны λ = 10 м (f=30 МГц).
2. Сопротивление нагрузки $Z_2=R_2-i,X_C=(200-i,265);Ом$.
4. Входное сопротивление линии, рассчитываемое по формуле (2.82), $Z_1=300,frac<(200-i,265)+i,300,tg72^circ><300+i,(200-i,265),tg72^circ>=(116<,>2+i,113<,>1);Ом$
Таким образом, сопротивление нагрузки $Z_2=(200-i,265);Ом$, обусловленное последовательно включенными емкостью и сопротивлением, трансформируется с помощью двухметровой линии, работающей на частоте 30 МГц, во входную нагрузку $Z_1=(116<,>2+i,113<,>1);Ом$, которая соответствует последовательно включенным сопротивлению (другой величины) и индуктивности L . Поэтому на рис. 2.37 между рассчитываемой линией и ее эквивалентом был по ставлен знак тождества. Индуктивность, сопротивление которой на частоте 30 МГц составляет 113,1 Ом, $L=frac<113<,>1><2pi>cdot<30>cdot<10^6>=0<,>602;мкГн$.
Для облегчения расчетов величин X L и Х C можно воспользоваться номограммами, приведенными на рис. 2.38.
Особо рассмотрим один частный случай, вытекающий из общей формулы (2.82), а именно длина линии l =λ/4 . В этом случае формула (2.82) значительно упрощается и принимает вид $$beginZ_1=fracendtag<2.87>$$
Эту формулу следует запомнить, так как она достаточно часто будет встречаться на практике. Сейчас применим эту формулу для конкретных примеров.
Пример 1. Требуется рассчитать входное сопротивление линии с волновым сопротивлением Z0=300 Ом, нагруженной на антенну с Z2=600 Ом, если длина линии l = λ/4 . Получаем $Z_1=frac<300^2><605>=150;Ом$.
Пример 2. Требуется рассчитать волновое сопротивление четвертьволновой линии, согласующей два коаксиальных кабеля с сопротивлениями Z1=50 Ом и Z2=75 Ом. Расчет проведем по формуле $Z_0=sqrt$.Подставляя в эту формулу исходные значения, получим, что Z0=61,2 Ом.
При проведении подобных расчетов удобно пользоваться номограммой, приведенной на рис. 2.39.
Нагруженные длинные линии могут быть рассмотрены как резонансные контура. Характер изменения нагрузки в таком контуре при изменении длины линии приведен на рис. 2.36. Резонанс в линии наступает, если длина линии l = n λ/4 . Для других длин, отличных от n λ/4 , линия представляет собой или индуктивность, или емкость.
Если длина короткозамкнутой на конце линии l λ/4 , то ее сопротивление носит индуктивный характер и определяется по формуле $$beginX_L=Z_0tgendtag<2.88>$$
В частном случае при l = λ/8 имеем: $klapproxfrac<pi><4>=45^circ$ и $tg=l$. Следовательно, X L = Z 0 . Другими словами, короткозамкнутая линия длиной l = λ/8 является индуктивностью, значение которой $L=frac<omega>$.
Если длина разомкнутой линии l λ/4 , то ее сопротивление носит емкостный характер и определяется по формуле $$beginX_C=Z_0tgendtag<2.89>$$
В частном случае, когда l = λ/8 , линия представляет собой емкость, значение которой $C=frac<1><omega>$.
В согласующих устройствах отрезки длинной линии часто используются в качестве индуктивности или емкости. Для удобства расчета можно пользоваться графиками, приведенными на рис. 2.40.
Пример. Требуется найти входное сопротивление короткозамкнутой линии длиной l=15 см, имеющей коэффициент укорочения K=0,905 и волновое сопротивление Z0=300 Ом для длины волны λ=2 м (150 МГц).
1. Электрическая длина линии определяется по формуле (2.12): l э =l / K= 15/0,905=16,6 см=0,166 м .
2. Фазовый сдвиг вдоль линии определяется по формуле (2.14): kl =2π l /λ=2π·0,166/2=0,52 рад или kl =2π l /λ=360°·0,083=29,9° .
3. Сопротивление X L= Z 0 tg 29,9°=300·0,577= 173 Ом .
4. Индуктивность Z = X L/ ω = 173/2π·150·10 6 =0,183 мкГн.
5. Та же самая линия, только разомкнутая, имеет сопротивление X C =Z 0ctg 29,9°=300·1,73=520 Ом , что эквивалентно емкости С=1/ω Х C=2,04 пф .
При проведении подобных расчетов удобно пользоваться графиками, приведенными на рис. 2.40.Так, например, для фазового сдвига kl= 30° по графикам на рис. 2.40 определяем, что X L /Z 0 = 0,57 и X C/ Z 0=1,75 . Следовательно, X L = 300·0,57=171 Ом и X C=300·1,75=525 Ом . Тогда, пользуясь графиками, приведенными на рис. 2.38, находим, что L =0,19 мкГн и С =2,1 пФ . Эти результаты отличаются (с малой погрешностью) от приведенных расчетных данных. Однако полученная точность определения параметров L и С является достаточной для целей практики.
Отметим еще одно обстоятельство, вытекающее из ранее приведенных рассуждений о различном характере разомкнутой и замкнутой линий. Речь идет о способе измерения волнового сопротивления линии. Для этого достаточно определить эквивалентные индуктивности и емкости при короткозамкнутой и разомкнутой линиях. Эти измерения, как известно, провести нетрудно. Тогда, зная значения измеренных L и С , можно вычислить волновое сопротивление линии: $$beginZ_0=sqrt=sqrt<frac>endtag<2.90>$$
В реальных линиях всегда присутствуют потери. Это обстоятельство, как было показано ранее [см. формулу (2.35)], приводит к изменению значения волнового сопротивления линии. Кроме того, наличие потерь приводит к изменению характера распределения вдоль линии падающей, а также отраженной волны. На рис. 2.41 показано влияние затухания на характер распределения напряжения вдоль длинной линии.
Длинная линия как резонансный контур
В диапазоне УКВ длинная линия может быть использована в качестве резонансного контура. Добротность такого контура (при малом уровне потерь) [19] $$beginQ=frac<2pi>=frac<2alpha>endtag<2.91>$$ где k — волновое число; α — затухание.
Для коаксиальной линии, как это было показано ранее, минимальные потери соответствуют условию D / d= 3,6 , т. е. волновому сопротивлению Z 0=77 Ом . На рис. 2.42 приведены графики добротности как функции внешнего диаметра коаксиального кабеля и частоты. Эти графики построены для коаксиальной линии, выполненной из меди и имеющей воздушную изоляцию.
Целесообразно обратить внимание на следующую информацию:
1. Входное сопротивление четвертьволновой линии без потерь или линии, длина которой кратна (2 n +1)λ/4 , имеет следующие значения: для короткозамкнутой Z1=∞ (параллельный резонансный контур), для разомкнутой Z1=0 (последовательный резонансный контур).
2. Для линии с потерями входное сопротивление четвертьволновой линии определяется по следующим формулам: для последовательного резонансного контура $$beginZ_1=Z_0(2n+1)frac<pi><4>Qapprox>endtag<2.92>$$ для параллельного резонансного контура $$beginZ_1=frac<4,Z_0Q><2n+1>piapproxfrac<alpha>endtag<2.93>$$
3. Частотная характеристика четвертьволновой линии вблизи резонансной частоты очень похожа на обычную частотную зависимость при резонансе контура с добротностью Q . Однако следует иметь в виду, что входное сопротивление длинной линии в этой области изменяется несколько иным образом, чем сопротивление резонансного контура, образованного сосредоточенными индуктивностью и емкостью.
При небольшом отклонении частоты Δf от резонансной частоты f рез появляется дополнительный фазовый сдвиг $$begindelta=frac<(2n+1)pi><4>-frac<2piDeltal>endtag<2.94>$$
Изменение входного сопротивления при небольшом отклонении частоты Δf от резонансной зависит как от длины линии l и ее затухания α , так и от дополнительного фазового сдвига δ . Для последовательного резонансного контура входное сопротивление $$beginZ_<вх>approxsqrt<(alpha)^2+delta^2>=alphaZ_0sqrt<1+left(frac<delta><alpha>right)^2>endtag<2.95>$$ для параллельного резонансного контура $$beginZ_<вх>approxleft[(alpha)^2+delta^2right]^<-frac<1><2>>=frac<alphasqrt<1+left(frac<delta><alpha>right)^2>>endtag<2.96>$$
Из анализа этих формул следует, что при условии $alpha=delta$ входное сопротивление линии, соответствующее последовательному резонансному контуру, в 1,4 раза больше, чем значение Z 1 , рассчитанное по формуле (2.92). Более полную информацию по данному вопросу можно найти в [19, 20].
Источник
Определение длин лэп
Для варианта №1
Рис 2.
Схема соединения. Вариант № 1
L∑
= 245,76
км
Для
варианта №2
Рис 3.
Схема соединения. Вариант № 2
L∑
= 246,18 км
Для
варианта №3
Рис 4.
Схема соединения. Вариант № 3
L∑
= 253,76 км
Для
варианта №4
Рис 5.
Схема соединения. Вариант № 4
L∑
= 303,8 км
Для
варианта №5
Рис 6.
Схема соединения. Вариант № 5
L∑
= 258,27 км
Для
варианта №6
Рис 7.
Схема соединения. Вариант № 6
L∑
= 327,28 км
Для
варианта №7
Рис 8.
Схема соединения. Вариант № 7
L∑
= 354,23 км
Для
варианта №8
Рис 9.
Схема соединения. Вариант № 8
L∑
= 285,98 км
Для
варианта №9
Рис 10.
Схема соединения. Вариант № 9
L∑
= 290,01 км
Для
варианта №10
Рис 11.
Схема соединения. Вариант № 10
L∑
= 309,47 км
Таблица № 2
Сравнение вариантов конфигурации сети
|
№ варианта |
L |
Примечания |
|
1 |
245,76 |
Схема |
|
2 |
246,18 |
Схема |
|
3 |
253,76 |
Схема |
|
4 |
303,8 |
Схема |
|
5 |
258,27 |
Схема |
|
6 |
327,28 |
Схема |
|
7 |
354,23 |
Схема |
|
8 |
285,98 |
Схема |
|
9 |
290,01 |
Схема |
|
10 |
309,47 |
Схема |
Выбраны варианты
№№ 1,2,3 – по минимальной длине и простоте
конфигурации сети.
После
расчета задачи ПРАМ, выбора U
ном, расчета токов нормального и
максимального режимов и выбора марок
проводов для вариантов 1,2,3 выяснилась:
необходимость введения в них двухцепных
линии (после проверки выбранных марок
проводов по условиях I
дд. ), в результате L
∑ выбранных
вариантов изменились. См.
Таблицу №
2
Таблица №2
продолжение
|
№ варианта |
L |
Введенные |
Полученная |
|
1 |
245,76 |
245,76 |
|
|
2 |
246,18 |
246,18 |
|
|
3 |
253,76 |
253,76 |
По условию
минимальной суммарной длины линий,
наиболее выгодным вариантом является
вариант № 10. Вариант № 2, является более
простыми по взаимному расположению
источников питания и нагрузок.
Соседние файлы в папке курсач docx180
- #
- #
- #
07.08.2013337.18 Кб72puanson_kursach.docx
- #
- #
- #
- #
- #
- #
- #
- #
Для расчта установившихся режимов ЛЭП расчитывают схемы замещения линии электропередачи. При расчете последних принимают допущение, что для линий электропередач небольшой длины (при частоте 50 Гц границей можно считать длину 300 км) распределёность параметров можно не учитывать и можно использовать более простое представление в виде схемы замещения с сосредоточенными параметрами. В данной статье рассмотрен расчет длинной линии электропередачи, которая моделируется как несколько последовательно включенных ЛЭП, длиной менее 300 км.
Содержание
- 1 Постановка задачи
- 1.1 Расчёт параметров схемы замещения ЛЭП
- 1.2 Расчёт УРов в ПК RastrWin
- 1.3 Построение графиков
- 2 Файлы для скачивания
Постановка задачи
Требуется:
- Рассчитать возможные допустимые УРы при [math] displaystyle L=1000,1500,2000 text{ км}[/math] и различных мощностях нагрузки [math](displaystyle Р=0…1000 text{ МВт ; }displaystyle Q=0…500 text{ Мвар});[/math]
- Построить семейства [math] displaystyle U=f(L)[/math] для каждой мощности нагрузки S.
Расчёт параметров схемы замещения ЛЭП
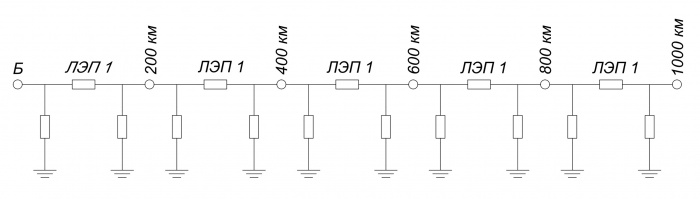
Схемы для расчета УР линий длиной 1000, 1500 и 2000 км представлены соответственно на рисунках 1, 2 и 3.
Рисунок 1. Схема замещения ЛЭП длиной 1000 км.
Рисунок 2. Схема замещения ЛЭП длиной 1500 км.
Рисунок 3. Схема замещения ЛЭП длиной 2000 км.
Справочные данные для расчёта параметров ЛЭП приведены здесь.
Описание схемы замещения ЛЭП приведено здесь.
- ЛЭП 1
- [math]displaystyle L=200[/math] км — протяженность линии;
- [math]displaystyle N=1[/math] — количество цепей;
- [math]displaystyle m=3[/math] — число проводов в фазе;
- [math]displaystyle R_{0}=2.9[/math] Ом/100км;
- [math]displaystyle X_{0}=30.8[/math] Ом/100км;
- [math]displaystyle ΔP_{к}=9000[/math] МВт;
- [math]displaystyle G_{0}=frac{ΔP_{к}}{U^2} = frac{9000}{250000} = 3.6cdot10^{-8}[/math] Cм/км;
- [math]displaystyle B_{0}= 360cdot10^{-6}[/math] См/км;
- [math]displaystyle R_{1}=R_{0}cdot frac{L}{100cdot {N}} = 2.9cdot frac{200}{100} = 5.8[/math] Ом;
- [math]displaystyle X_{1}=X_{0}cdotfrac{L}{100cdot {N}} = 30.8cdot frac{200}{100} = 61.6[/math] Ом;
- [math]displaystyle B_{1}=B_{0}cdot{L}cdot{N} = 7.2cdot{10^{-4}}[/math] См;
- [math]displaystyle G_{1}=G_{0}cdot{L}cdot{N} = 7.2cdot{10^{-6}}[/math] См;
- ЛЭП 2
- [math]displaystyle L=100[/math] км — протяженность линии;
- [math]displaystyle N=1[/math] — количество цепей;
- [math]displaystyle R_{2}=R_{0}cdot frac{L}{100cdot {N}} = 2.9cdot frac{100}{100} = 2.9[/math] Ом;
- [math]displaystyle X_{2}=X_{0}cdotfrac{L}{100cdot {N}} = 30.8cdot frac{100}{100} = 30.8[/math] Ом;
- [math]displaystyle B_{2}=B_{0}cdot{L}cdot{N} = 3.6cdot{10^{-4}}[/math] См;
- [math]displaystyle G_{2}=G_{0}cdot{L}cdot{N} = 3.6cdot{10^{-6}}[/math] См;
Расчёт УРов в ПК RastrWin
Результаты расчетов представлены в таблицах 1, 2 и 3.
| Длина линии, км | U, кВ | |||||||
|---|---|---|---|---|---|---|---|---|
| S=0 | S=50+j25 | S=100+j50 | S=150+j75 | S=200+j100 | S=250+j125 | S=350+j175 | S=500+j250 | |
| 0 | 500 | 500 | 500 | 500 | 500 | 500 | 500 | 500 |
| 200 | 671.43 | 666.77 | 661.22 | 656.22 | 650.12 | 643.44 | 631.85 | 589.48 |
| 400 | 813.93 | 805.13 | 795.63 | 785.31 | 773.88 | 761.38 | 739.31 | 660.24 |
| 600 | 920.67 | 908.28 | 894.93 | 880.47 | 864.52 | 847.09 | 815.9 | 706.48 |
| 800 | 986.72 | 971.37 | 954.87 | 937.06 | 917.45 | 896.08 | 857.45 | 713.72 |
| 1000 | 1009.08 | 991.47 | 972.62 | 952.33 | 930.07 | 905.86 | 861.73 | 724.8 |
| Длина линии, км | U, кВ | ||||||
|---|---|---|---|---|---|---|---|
| S=600+j300 | S=700+j350 | S=800+j400 | S=900+j450 | S=1000+j500 | S=1100+j550 | S=1200+j600 | |
| 0 | 500 | 500 | 500 | 500 | 500 | 500 | 500 |
| 200 | 532.15 | 540.23 | 548.68 | 557.48 | 566.65 | 576.24 | 586.28 |
| 400 | 553.52 | 573.28 | 594.22 | 616.29 | 639.52 | 664 | 689.77 |
| 600 | 561.03 | 594.17 | 629.26 | 666.18 | 704.93 | 745.61 | 788.27 |
| 800 | 553.22 | 599.86 | 648.92 | 700.22 | 753.76 | 809.64 | 867.93 |
| 1000 | 530.17 | 589.03 | 650.43 | 714.19 | 780.34 | 848.99 | 920.27 |
| 1200 | 493.44 | 561.99 | 632.9 | 706.06 | 781.57 | 859.59 | 940.33 |
| 1400 | 446.29 | 520.67 | 597.18 | 675.75 | 756.57 | 839.86 | 925.89 |
| 1500 | 420.52 | 495.91 | 573.39 | 652.9 | 734.65 | 818.87 | 905.83 |
| Длина линии, км | U, кВ | |||
|---|---|---|---|---|
| S=600+j300 | S=700+j350 | S=800+j400 | S=900+j450 | |
| 0 | 500 | 500 | 500 | 500 |
| 200 | 557.08 | 553.47 | 548.01 | 539.58 |
| 400 | 603.37 | 600.89 | 595.76 | 586.36 |
| 600 | 633.15 | 635.29 | 634.91 | 630.49 |
| 800 | 643.03 | 652.3 | 659.78 | 664.53 |
| 1000 | 631.5 | 649.6 | 666.95 | 683.47 |
| 1200 | 598.98 | 626.71 | 654.95 | 684.45 |
| 1400 | 547.29 | 584.88 | 624.11 | 666.52 |
| 1600 | 480.39 | 527.27 | 576.57 | 630.57 |
| 1800 | 404.82 | 459.29 | 516.52 | 579.41 |
| 2000 | 331.52 | 389.69 | 450.76 | 518.05 |
Построение графиков
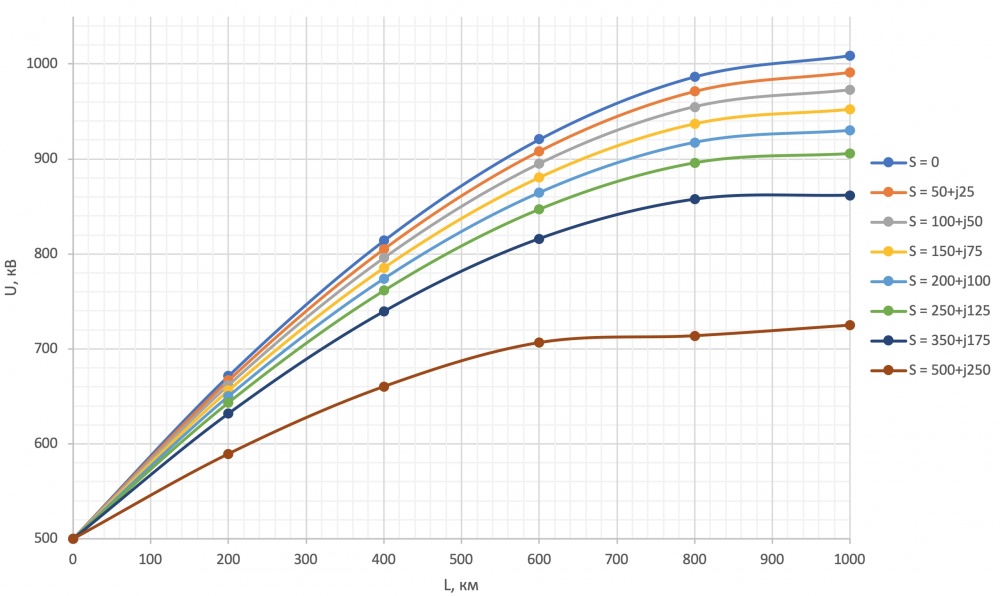
- Рисунок 4 – Семейство кривых [math] displaystyle U=f(L)[/math] для каждой мощности S при [math] displaystyle L=0…1000 text{ км}[/math]
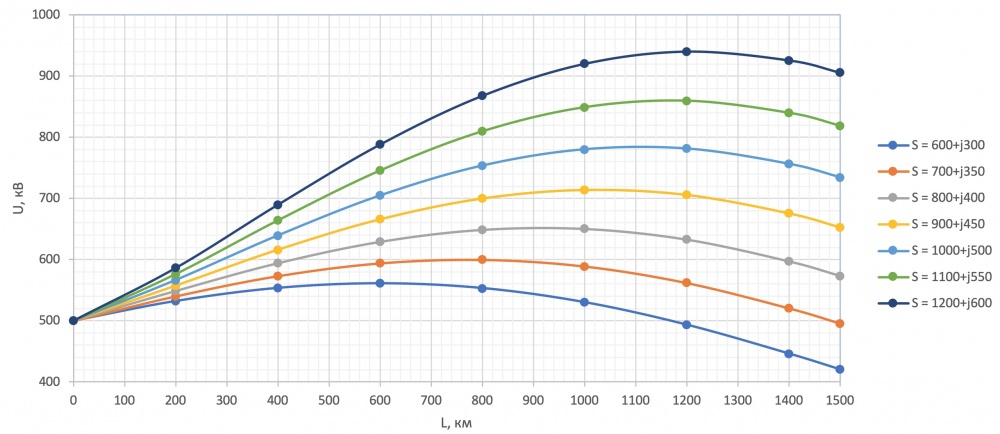
- Рисунок 5 – Семейство кривых [math] displaystyle U=f(L)[/math] для каждой мощности S при [math] displaystyle L=0…1500 text{ км}[/math]
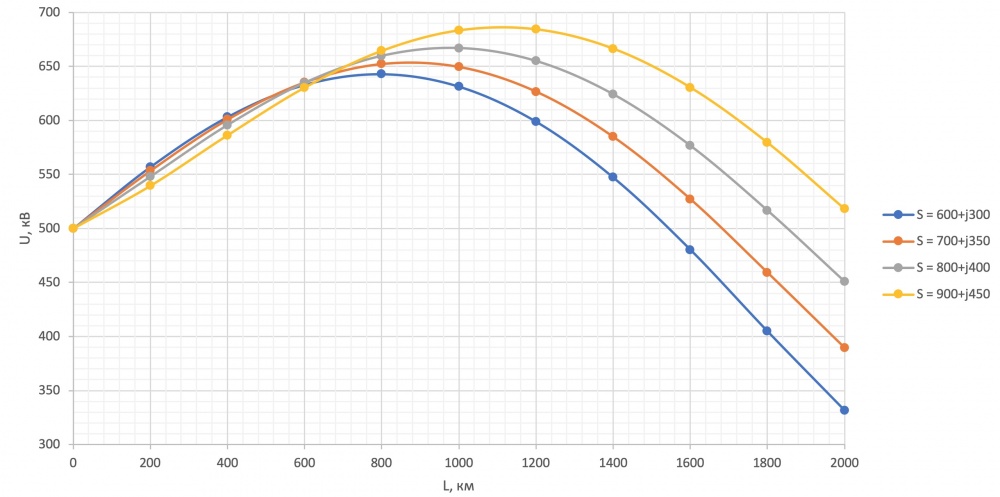
- Рисунок 6 – Семейство кривых [math] displaystyle U=f(L)[/math] для каждой мощности S при [math] displaystyle L=0…2000 text{ км}[/math]
Файлы для скачивания
Файл:Длинные ЛЭП.zip
ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ:
|
№№ ПС |
Нагрузка при напряжении |
tg |
Состав нагрузки по |
Tмах,ч |
Напряжение на шинах ПС – А, кВ |
||||||
|
6-10 кВ |
110 кВ |
I |
II |
III |
Uнб |
Uнм |
|||||
|
Pнб, МВт |
Pнм, МВт |
Pнб, МВт |
Pнм, МВт |
||||||||
|
А |
1,050 |
1,060 |
|||||||||
|
9 |
0 |
0 |
1,6 |
0,8 |
0,4 |
0 |
70 |
30 |
4300 |
||
|
10 |
0 |
0 |
1,3 |
0,7 |
0,38 |
0 |
75 |
25 |
4700 |
||
|
11 |
6,5 |
3,2 |
1,5 |
0,8 |
0,37 |
20 |
65 |
15 |
6000 |
||
|
12 |
0 |
0 |
1,3 |
0,7 |
0,39 |
0 |
65 |
35 |
5200 |
Климатический район по
гололеду: _________4_____________
Коэффициент приведения
цен: ______________________
Стоимость потерь
электроэнергии: _____________ руб./кВт·ч
Принципиальные схемы
соединения подстанций:
|
Вариант 1 |
Вариант 2 |
|
|
|
ГЛАВА 1. РАСЧЕТ ДЛИНЫ ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ ПО ИЗВЕСТНЫМ
КООРДИНАТАМ УЗЛОВ НАГРУЗКИ
Расчет длины
трасс воздушных линий электропередач (ВЛ) производится по выражению:
|
|
(1.1) |
где i, j – номера подстанций, связанных воздушной
линией электропередачи ;
xk,
yk – координаты k-й подстанции;
1,3 –
коэффициент, учитывающий отклонения трассы ВЛ от прямой.
Дальнейший
расчёт длины линий приведён в виде таблиц 1.1 и 1.2. Структурные схемы
сравниваемых вариантов в масштабе 1:2000000 приведены на рисунках 1.1,1.2.
|
Таблица 1.1 Определение длины |
|||||||||
|
ПС |
Координаты ПС |
ПС |
Длины трасс ВЛ (по формуле |
||||||
|
x |
y |
9 |
10 |
11 |
12 |
0 |
|||
|
А |
7,5 |
20,5 |
А |
11,7 |
– |
– |
– |
– |
|
|
9 |
7,5 |
11,5 |
9 |
– |
5,6 |
9,8 |
– |
||
|
10 |
11,2 |
2,5 |
10 |
– |
– |
– |
– |
||
|
11 |
3,5 |
7,5 |
11 |
– |
– |
– |
– |
||
|
12 |
3,5 |
2,5 |
12 |
– |
– |
– |
|||
|
0 |
5,9 |
7,9 |
0 |
– |
7,5 |
– |
– |
|
Таблица 1.2 Определение длины |
||||||||
|
ПС |
Координаты ПС |
ПС |
Длины трасс ВЛ (по формуле |
|||||
|
x |
y |
9 |
10 |
11 |
12 |
|||
|
А |
7,5 |
20,5 |
А |
11,7 |
– |
– |
– |
|
|
9 |
7,5 |
11,5 |
9 |
9,7 |
5,6 |
– |
||
|
10 |
11,2 |
2,5 |
10 |
– |
9,1 |
7,7 |
||
|
11 |
3,5 |
7,5 |
11 |
– |
– |
– |
||
|
12 |
3,5 |
2,5 |
12 |
– |
– |
– |
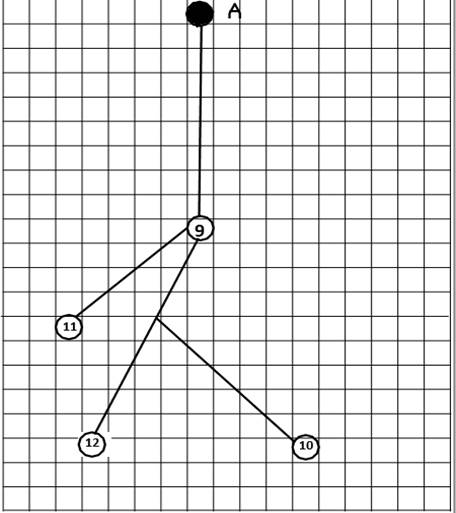
Рисунок 1.1 – Структурная
схема сравниваемого варианта электрической сети (вариант1- радиальная схема)
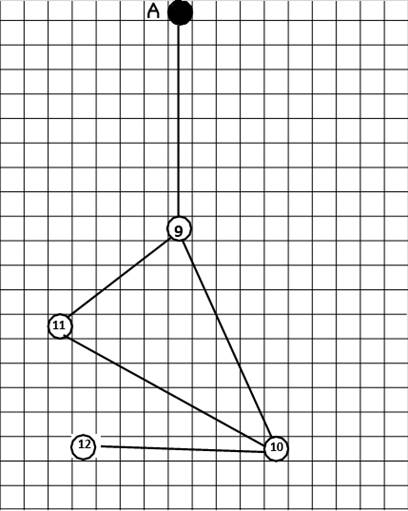
Рисунок
1.2 – Структурная схема сравниваемого варианта электрической сети
(вариант2-кольцевая схема)
2. ОЦЕНОЧНЫЙ
РАСЧЕТ ПОТОКОРАСПРЕДЕЛЕНИЯ АКТИВНОЙ И РЕАКТИВНОЙ МОЩНОСТИ
Вычисление
потокораспределения начинаем с составления расчетной схемы, на которую
нанесены:
– источник питания сети –
центр питания А;
– понижающие подстанции – узлы
подключения нагрузок.
meraBOT
Мастер
(1138)
10 лет назад
климатический район, ветровые нагрузки, расположение (повороты, разница стрел провеса) напрямую влияют на длину пролета, также работают экономические соображения
Бывший студентГуру (2653)
10 лет назад
А как с их помощью узнать точную длину пролета? ПУЭ перелистал, не смог найти.
meraBOT
Мастер
(1138)
тебе для курсового? есть стандартная длина пролета, если ветренный район (например степь) то провода будут схлестываться, если район гололедный то на длинных пролетах провода могут оборваться и тд. может тебе это для рассчета нах и не надо тк я проектировал по учебе только контактную сеть жд.
смотри кароче тут. может поможет
http://energoproekt.blogspot.ru/2009/04/prolety-vozdushnyh-liniy.html
http://www.energetik-ltd.ru/statii/pue/25
тут еще метода какаята, угощайся:
http://window.edu.ru/resource/718/29718/files/amursu013.pdf