Как найти длину линии геодезия

При вычислении
длин линий в результат измерения вводят
поправки, которые исключают влияние
система­тических погрешностей.

Поправка
∆D_к
за
компарирование мерного прибора.
При измерении линий фактическая длина
мерного при­бора отличается от номинала
на величину поправки за компарирование

l
= l₀
+ ∆l_к.
Оцифровка мерного при­бора соответствует
номиналу, поэтому результат измере­ния
остатка обозначим через r₀.
В этом случае фактиче­ская длина
остатка r
за счет
поправки за компарирование изменится
на величину, пропорциональную длине
остат­ка, т. е.

r
= r₀
+ (∆_к/l₀)r₀

(26.1)

Аналогичное
равенства можно записать для отрезка,
чья длина кратна номинальной длине
ленты l₀

D
= n(l₀
+ ∆l_к),
(26.2)

где n
– число целых мерных лент, отложенных
в процессе измерения отрезка.

Полная длина линии
запишется как сумма (24.1) и (24.2)

D
= n(l₀
+ ∆l_к)
+ (r₀
+

r₀).
(26.3)

Раскроем скобки
и перепишем формулу (24.3) в несколько
ином виде

D
= (nl₀
+ r₀)
+

_к.
(26.4)

Величина (nl₀
+ r₀)
– эта длина линии, вычисленная с
номинальным значением длины мерного
прибора. Обозначив ее через D₀,
запишем

D
= D₀
+ (D₀/l₀)∆l_к
.

Величину

∆D_к
= D
– D₀
= (D₀/l₀)∆l_к

называют поправкой
в длину мерного прибора за компарирование.

Поправка
∆D
_t за
температуру
мерного
прибора.
При измерении линий температура мерного
прибора t
обычно
отличается от температуры компарирования
t₀.
В этом случае длина мерного прибора
равна

l
= l₀
+ α(t
– t₀)l₀

где α
–
коэффициент
линейного расширения материала мерного
прибора (для стали α
= 12,5.10^-6).

Соответственно
изменится длина остатка

r
= r₀
+ α(t –
t₀)r₀.

С учетом предыдущего
соотношения получим уравнение, учитывающее
поправку за температурное расширение
прибора.

D
= (nl₀
+ r₀)
+ α (t –
t₀)
(nl₀
+ r₀),

но nl₀
+ r₀
=D₀,
тогда

D
= D₀
+ α (t
– t₀)
D₀.

Величину

∆D_t
= D
– D₀
= α(t
– t₀)D₀.

называют поправкой
в длину линии за температуру мер­ного
прибора.

Если при измерении
линий для создания топографиче­ских
планов разность температур по абсолютной
величине не превышает 8º, то поправку
за температуру не учиты­вают. При
учете поправок обычно измеряют температуру
воздуха, а не мерного прибора. Возникающая
при этом погрешность мала и не влияет
на точность измерений.

При измерении длин
линий на конструкциях зданий и сооружений
дополнительно учитывают температурные
расширения конструкций. Если температуру
конструкций при эксплуатации обозначить
через t_э,
то поправку за температуру можно
вычислить по формуле

∆D_t
= ∆α(t_ср–
t_э)D₀
+ ∆tα_срD₀,
(26.5)

где α_ср,
t_ср
– средние
значения соответственно коэффи­циентов
линейного расширения и температур
конструк­ций и мерного прибора; ∆α,
∆t
– разности
коэффициентов линейного расширения и
температур конструкций мерного прибора.

Поправку по формуле
(26.5) учитывают при выполнении высокоточных
линейных измерений на конструкциях
уникальных сооружений.

На объектах массовой
застройки из сборных железо­бетонных
конструкций разность коэффициентов
линейного расширения ∆α.
близка к
нулю (0,5.10^-6),
поэтому пер­вый член правой части
равенства (26.5) мал. Тогда

∆D_t
= ∆tα_срD₀.

Наибольшие
затруднения при измерениях вызывает
определение температуры конструкций,
так как для этого приходится в них делать
лунки. Поэтому поправки по формуле
(26.5) учитывают только при возведении
зданий повышенной этажности и промышленных
сооружений с пролетами между опорами
более 6м.

На типовых зданиях
массовой застройки для упро­щения
вычислений и измерений значения поправок
метро­вых делений прибора приводят
к значениям температуры эксплуатации
здания, что позволяет обойтись без учета
температуры.

Поправка
∆D_ν,h
за приведение линии к горизонту.
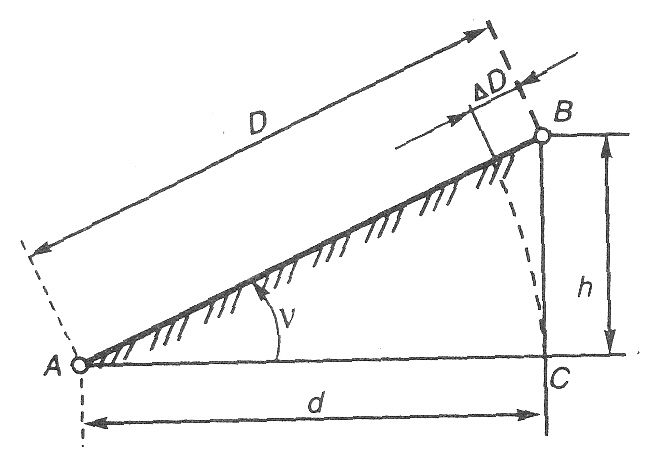
Горизонтальное положение d
наклонной
линии D
находят по углу наклона v
или по превышению h
(рис. 31).

Если известен угол
наклона, то из прямоугольного треугольника
АВС имеем

d
= D
cos ν.

Рис.
31. Поправка за приведение линии к
горизонту

При вычислениях
горизонтальных проложений исполь­зуют
микрокалькуляторы. При отсутствии
микрокальку­лятора для упрощения
вычислений в результаты измере­ний
вводят поправку

∆ D_ν
= d
– D
= – D(1
– cosν)
= –2D
sin(ν/2)

Поправка за
приведение линий к горизонту всегда
отрицательна,, так как горизонтальное
проложение всегда меньше длины наклонной
линии.

При углах наклона
менее 10º синус изменяется про­порционально
значениям угла. Поэтому sin (v/2)≈
0,5 sin
v.
Тогда

∆D_ν
= –0,5sin²ν

Если известно
превышение концов измеряемой линии, то
по теореме Пифагора (рис. 31)
имеем

D²
= d²
+h²;
h²
= D²
– d²
=
(D
– d)
(D
+ d).

При вычислениях
поправки обычно удерживают две­–три
значащие цифры, поэтому можно принять
d≈D.
Если учесть, что ∆D_h
= d
– D,
то

∆D_h
= – h²/2D

(24.6)

Если линия имеет
перегибы ската, то поправки за приведение
к горизонту вычисляют по частям. При
этом линию разбивают на отрезки с
равномерными скатами, а поправку для
каждого отрезка вычисляют раздельно
по формуле (24.6).

Окончательно
горизонтальное проложение линии с
уче­том всех поправок вычисляют по
формуле

d
= D₀
+ ∆D_к
+ ∆D_t
+ ∆D_ν,h.

При измерении
линий могут быть допущены промахи и
грубые погрешности. Один вид промахов
(оцифровку делений) был отмечен выше.
Существует еще целый ряд погрешностей,
влияние которых на суммарный результат
измере­ний можно существенно уменьшить.
Эти погрешности носят си­стематический
характер по влиянию на результат, но
случайны по величине. Чтобы уменьшить
их величины, необходимо учиты­вать
следующее.

1. Отклонение концов
рулетки от створа измерений всегда
увеличивает измеряемую длину. Чем меньше
отклоняются концы от створа, тем меньше
погрешность измерения. При измерениях
для многих целей укладку мерных приборов
в створ производят с использованием
оптических труб. К такому приему прибегают
в тех случаях, когда хотят получить
результат с относительной погрешностью
менее 1:3000 от измеряемой длины. Отклонения
от створа концов 30 и 50-метровых рулеток
более чем на 0,15м
недопустимы.

2. Большую погрешность
в измеряемую длину может внести разное
натяжение прибора при эталонировании
и практической работе. Следует избегать
избыточного натяжения, так как тонкое
полотно рулеток растягивается, при этом
часто не восстанавли­вая начальную
длину. Достаточно точно (до ± 100 Н) можно
вы­держать натяжение, используя для
этого ручные приборы – ди­намометры
типа ПН-2 или пружинные бытовые весы.

3. Недопустимо
ослаблять внимание при отсчитывании
по кон­цам мерного прибора или его
фиксации. Достигнутая точность может
быть утрачена при неодновременном
снятии отсчетов, под­вижке мерного
прибора во время фиксации его концов.
Поэтому не следует пренебрегать
возможностью дважды или даже трижды
взять отсчеты по концам мерного прибора
и сравнить разности от­счетов по
переднему и заднему концам (П – 3).
Разность отсчетов (для одного пролета
измерений) при работе рулетками не
должна превышать 2мм, а при измерении
мерными лентами – 1см.

4. Необходимо
следить не только за превышением концов
мер­ного прибора, но и за его изгибом
в вертикальной плоскости. Точ­ность
определения поправки за наклон зависит
от точности опре­деления превышений:
чем короче линия, тем точнее надо знать
превышение. Как правило, достаточно его
знать с погрешностью до 1,0…1,5 см на 100м
длины.

5. При введении
поправок за отличие температуры, данной
в урав­нении рулетки (+20С^º),
и температуры измерений следует помнить,
что измеряют температуру воздуха, а
поправку вводят за изменение температуры
металлического полотна мерного прибора.
Поэтому при прямом солнечном облучении
мерного прибора термометр подкла­дывают
под его полотно и держат 3…5 мин. с тем,
чтобы точнее определить температуру
мерного полотна. Разность температуры
воз­духа и мерного прибора измеряют
с погрешностью не грубее 5 С^º.

6. Существенно
исказить результат измерения может
плохое за­крепление точек, между
которыми ведется измерение. Вязкая
поч­ва, зыбко забитые кол, штырь или
шпилька, изменяющие свое положение от
случайных ударов, приводят к появлению
недопу­стимых погрешностей в измеряемой
длине. Назад

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  12.03.20156.3 Mб35Краткий курс аналитической геометрии.pdf

• #
• #
• #
• #
• #
• #

8.1. Измерение длин линий мерными лентами и рулетками

Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.

Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.

Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.

Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.

Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.

Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.

Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:

l = l₀ + Dl + a l₀ (t– t₀). (8.1)

Здесь l – длина ленты при температуре t; l₀ – номинальная длина; Dl – поправка к номинальной длине при температуре компарирования t₀ ; a – температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.

Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.

Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане).

Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D – вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D₁, то есть в створ точек C и B. Затем из точки С веху переносят в точку С₁ и так далее до тех пор, когда обе вехи окажутся в створе AB.

Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n – число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).

Длину измеряют дважды – в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях – 1/1000). За окончательное значение принимают среднее.

Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.

Поправка за компарирование определяется по формуле

D_k = n Dl ,

где Dl – отличие длины ленты от 20 м и n – число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.

Поправка за температуру определяется по формуле

D_t = aD(t–t₀)

где a – термический коэффициент расширения (для стали a = 0,0000125); t и t₀ – температура ленты во время измерений и при компарировании. Поправку D_t учитывают, если ½t–t₀½>10°.

Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D

d = D cosn , (8.2)

где n – угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где

D_n = d – D = D (cosn – 1) = -2D sin² . (8.3)

По формуле (8.3) составляют таблицы, облегчающие вычисления.

Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.

Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.

Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.

Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами – глазным 1 и предметным 4.

Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона

Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 – 30¢.

Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.

Точность измерений лентой в разных условиях различна и зависит от многих причин – неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.

Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.

Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта d_i определяют по формуле

d_i = П – З,

где П и З – передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).

Если линия имеет наклон, необходимо учесть поправку

,

где h – превышение между концами пролёта, измеряемое нивелиром.

Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 – 1:10000.

ЛАБОРАТОРНАЯ
РАБОТА №1

«Измерение
длин прямых и извилистых линий по карте»

Цель
работы: научиться измерять прямые и извилистые
линии на карте с помощью циркуля измерителя, курвиметра, поперечного масштаба.

Прямые
линии измеряют обычно линейкой. Извилистые и ломаные
линии измеряют по частям, циркулем – измерителем. Для этого устанавливают по линейке
или линейному масштабу раствор циркуля, соответствующий какому – нибудь целому
числу километров или сотен метров, и таким “шагом” проходят вдоль
измеряемой линии, ведя счёт перестановок ножек. Порядок измерений показан на
рис. 2, где AF – измеряемая линия, A, B, C, D, E – места постановки ножек, EF –
остаток, измеряемый по линейке (линейному масштабу). Стрелками показано
направление перемещения ножек.

Рис.1 Измерение линий
“шагом” циркуля.

Величину
“шага” выбирают в зависимости от извилистости линий: от 4-5 см – при
измерении кривых с плавными закруглениями до 1-2 см – при измерении линий с
большим числом резких поворотов.
Для измерения кривых и извилистых линий используют также специальный
прибор – курвиметр (рис. 2). Механизм этого прибора состоит из измерительного
колёсика, соединённого системой зубчатых передач со стрелкой, которая движется
по циферблату. При движении колёсика вдоль измеряемой по карте линии стрелка
передвигается по циферблату и указывает пройденное колёсиком расстояние в см.
Для измерения расстояния следует предварительно вращением колёсика установить
стрелку курвиметра в начальное положение, т.е. на отсчёт “0”, а затем
прокатить его вдоль измеряемой линии, следя за тем, чтобы стрелка двигалась по
циферблату в направлении чисел 10, 20, 30 и т.д. Умножив величину масштаба
карты на показания стрелки курвиметра, получают расстояние на местности.

Для
более точного измерения и откладывания расстояний по карте, применяют поперечный
масштаб – специальный график, награвированный на металлической линейке
(рис. 3) и выполненный под карту масштаба 1:50 000, т.к. цифры указывают
непосредственно расстояния на местности в км, сотнях и десятках м.
соответственно.

Рис. 3 поперечный масштаб на
транспортире

Рис.4 Поперечный масштаб.

Пользование
поперечным масштабом показано на рис. 4а. Пусть требуется определить расстояние
на местности, соответствующее отрезку de на карте масштаба 1:25 000. Раствор
циркуля, равный этому отрезку, устанавливают на поперечном масштабе так, чтобы,
во-первых, обе ножки оказались на одной горизонтальной линии и, во – вторых,
правая ножка находилась на одном из перпендикуляров к основанию (точка e), а
левая – на одной из наклонных линий (точка d). Для 1:25 000 карты основание
масштаба соответствует 500 м, десятая доля основания – 50 м, сотая – 5 м. По
цифровым обозначениям линий видно, что этот от-резок равен:

500*1 +
50*3 + 5*6 = 680 м.

Опытным
путём установлено, что с помощью циркуля измерение прямолинейных отрезков на
карте и других чертежах не могут быть выполнены точнее, чем 0,2 мм. Расстояние
на местности, соответствующее 0,2 мм на карте, называется предельной точностью
масштаба карты. Однако точность определения расстояний по карте зависит не
только от точности измерений, но и от погрешностей самой карты, неизбежных при
её составлении и печатании, которые могут достигать 0,5 мм, а на картах горных
районов – 0,75 мм. Источниками ошибок измерений являются также помятость и
деформация бумаги. С учётом этого фактическая точность измерения прямых линий
на карте, как показывает практика, колеблется в пределах 0,5 – 1,0 мм, что в
масштабе 1:25 000 на местности составляет: 12-25 м, в масштабе 1:50 000 – 25-50
м, 1:100 000 – 50-100 м.

Измеренное по карте расстояние получается всегда несколько короче
действительного. Одна из причин этого состоит в том, что по карте измеряются
горизонтальные проложения, в то время как соответствующие им линии на местности
наклонные, т.е. длиннее своих горизонтальных проложений. Длина маршрута,
измеренная по карте, бывает короче действительной не только вследствие влияния
рассмотренной выше причины, но и потому, что в масштабе карты не всегда
возможно изобразить все извилины дорог. При составлении карт дороги, как правило,
спрямляются, и тем больше, чем мельче масштаб карты. Это особенно заметно на
картах горной и холмистой местности.

Задание1.
На предложенной преподавателем топографической карте
измерить расстояние между двумя пунктами. Определите вероятнейшее значение.

Методические
указания:

Иголки
йиркуля измерителя устанавливают в центры условных знаков, обозначающих
географические объекты. Разные условные знаки по разному центрируются (рис 5)

Прежде чем производить измере­ние, необходимо выяснить, сколько
мет­ров или километров на местности содер­жится в основании масштаба вашей
карты и какова точность карты, то есть скольким метрам соответствует наи­меньшее
деление левой части линейного масштаба (1/10 часть основания). Рас­твор
циркуля, равный расстоянию меж­ду заданными пунктами, прикладывают к линейному
масштабу. При этом правая игла циркуля должна находиться точно на одном из
штрихов линейного масшта­ба справа от нуля, а левая — в пределах левой от нуля
части линейного масшта­ба. Отсчет делают по левой игле измери­теля и суммируют
с отсчетом, сделан­ным по правой игле (рис.6).

Задание 2. На предложенной преподавателем топографиче­ской карте, пользуясь
данным на ней линейным масштабом, из­мерьте расстояние по дороге между двумя
пунктами.

Методические указания. При измерении ломаных линий
про­изводится измерение составляющих ее прямых отрезков способом, описанным в
задании 1. Результаты измерений всех прямых отрез­ков данной ломаной линии
суммируют. Это и будет расстояние ме­жду заданными пунктами по дороге.

Задание 3. По предложенной преподавателем топографиче­ской карте измерьте
длину отрезка реки. Измерения произвести двумя способами: а) циркулем-измерителем;
б) курвиметром. Ре­зультаты сравните. Сделайте выводы.

Методические указания. Измерение
извилистых линий произ­водится малым раствором циркуля-измерителя (1,0 мм, 2,0
мм, 4,0 мм). При выборе раствора циркуля руководствуются извилисто­стью измеряемой
линии. Для более извилистых линий следует вы­бирать меньший раствор

циркуля-измерителя. Раствор измерителя нужно устанавливать очень
тщательно по поперечному масштабу. При этом лучше пользоваться микро
измерителем (рис.7).

Выбрав и установив раствор микро измерителя, им «шагают» по
извилистой линии, считая

число пройденных «шагов». Зная, какой длине на местности
соответствует раствор циркуля, и ум­ножив ее на число «пройденных» по отрезку
реки шагов, определяют общую длину заданного от­резка реки (см. рис.7).
Измерения производят не менее двух раз и вычисляют среднее значение.

Такой способ при всей его
трудоемкости не дает истинных длин линий, особенно если изме­рения проводились
по средне масштабной карте, так как в результате генерализации извилистые линии
на карте укорочены по сравнению с действительными рас­стояниями. Кроме того,
перемещая циркуль-измеритель по извили­стой линии, измеряют не сами извилины, а
стягивающие их хорды (см. рис. 7.10). При уменьшении же раствора придется
сделать большее число «шагов», что приведет к увеличению систематиче­ской
ошибки измерений. Поэтому измерения извилистых линий проводят двумя разными
растворами. Тогда истинная длина изви­листой линии может быть вычислена по
формуле

L₀=L₁+(L₁–L₂)- k(L₁–L₂),

где L₁ и L₂ — длины, измеренные двумя разными растворами циркуля-измерителя d₁, и d₂. При этом d₁ > d₂; коэффициент k  рассчитывается из соотношения

k=

При измерении этого же отрезка реки курви­метром отсчет по нему
следует делать с точно­стью до 0,1 деления. Измерения так же, как и в первом
способе, следует проводить не менее двух раз.

Для измерения линии курвиметром находя­щееся  в  нижней  част 
прибора    колесика деление циферблата соответствует пути, пройденному
колесиком в 1 см. Пройденный путь в сантиметрах считывают по циферблату.
Измеренную по карте длину переводят в действительную (на мест­ности) величину,
умножив ее на основание масштаба карты, по ко­торой производились измерения.

Задание 4. По физической карте школьного атласа определи­те суммарную длину
всех рек в бассейне реки, указанной в одном из вариантов таблицы.

Варианты к заданию 10

Методические указания. Описанный в задании 3 способ
пооче­редного промера каждой отдельной линии делает такие измерения весьма
трудоемкими. В этом случае прибегают к косвенному изме­рению, основанному на
статистических закономерностях. Доказа­но, что если на группу произвольно
ориентированных на карте линий наложить сетку квадратов со стороной d, то число пересече­ний т извилистых линий со сторонами квадратов
будет пропорцио­нальным их суммарной длине ΣD_L:

ΣD_L= dm.

Таким образом, для подсчета суммарной длины извилистых линий на
некотором участке карты достаточно наложить на них прозрачную палетку с сеткой
квадратов и подсчитать число пересе­чений каждой линии со сторонами квадратов
(рис.8). Погреш­ность таких косвенных измерений

составляет 3%-5%.

Точность определения суммарной длины извили­стых линий возрастет,
если измерения произвести при разных положениях палетки. Тогда при N произведенных
измерений (числе наложений палетки) суммарная длина извилистых линий вычисля­ется
по формуле

ΣD_L= dm.

Поскольку точность из­мерений зависит от парамет­ра палетки d, числа наложе­ний N, плотности самих линий и их
взаимной ориен­тировки, следует внимательно подойти к выбору параметра палетки.
При этом также важен вы­бор масштаба карты. Очень мелкий масштаб карты дает
изображение речного бассейна в сильно обобщенном виде. На та­ких картах
присутствуют лишь притоки первого порядка (и то за­частую не все), и вследствие
этого суммарная длина рек бассейна заведомо меньше истинной. На картах более
крупного масштаба для проведения подобных  измерений потребуются значительные
по площади палетки. Кроме того, крупномасштабные карты не ото­бражают всего
бассейна больших рек.

Задание выполняют в тетради. Описывают последовательно все
действия. Полученные данные сравнивают с данными справоч­ных изданий. Вычисляют
погрешность косвенных измерений.

Необходимые принадлежности: Циркуль – измеритель, топографические карты, курвиметр.

Содержание отчета:

·        
Номер и название работы;

·        
Цель работы;

·        
Необходимые принадлежности;

·        
Результаты выполнения заданий;

·        
Ответы на контрольные вопросы.

Контрольные вопросы:

1.Как определить суммарную длину линий измеренных с помощью
палетки.

2.Как  можно измерить длину извилистой линии с помощью масштаба:

а) линейного;

б) поперечного.

Литература:

1. Е.А.Чурилова, Н.Н.Колосова «Картография с основами топографии»,
Дрофа 2010 г. (практикум).

2.Л.А.Фокина «Картография с основами топографии» (практикум),
М.,ИЛЕКСА 2009 г.

3.Н.Ф.Самолетов «Руководство по выполнению лабораторных и
практических работ по геодезии», Федеральная служба России по гидрометеорологии
и мониторингу окружающей среды, 1998 год.

Обновлено: 18.05.2023

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

ЛЕКЦИЯ № 5

Приборы для непосредственного измерения линий. Компарирование мерных приборов. Вешение линий. Порядок измерения линий .

Целью линейных измерений является определение горизонтальных расстояний (проложений) между точками местности .

Непосредственный способ основан на непосредственном измерении линий местности механическими линейными приборами, к которым относятся мерные ленты, рулетки и проволоки. Процесс измерения длин линий непосредственным способом состоит в последовательном откладывании мерного прибора в створе линии.

Измерения линий на местности могут выполняться непосредственно, путем откладывания мерного прибора в створе измеряемой линии, с помощью специальных приборов дальномеров и косвенно. Косвенным методом измеряют вспомогательные параметры (углы, базисы), а длину вычисляют по формулам.

Приборы для непосредственного измерения линий

Для измерения длин линий посредством откладывания мерного прибора используют стальные мерные ленты, которые обычно изготавливают из ленточной углеродистой стали. В геодезической практике чаще всего применяются штриховые и шкаловые ленты.

Штриховые ленты имеют длину 20 и 24 м, ширину 15 – 20 мм и толщину 0,3 – 0,4 мм.

На ленте нанесены метровые деления, обозначенные прикрепленными бляшками, и дециметровые деления, обозначенные отверстиями. Метровые деления на обеих сторонах оцифрованы. Счет оцифровки делений ведется на одной стороне от одного конца ленты, а на другом – от другого конца. За длину ленты принимают расстояние между штрихами, нанесенными на крюках у концов ленты. К крюкам приделаны ручки. К ленте прилагается 6 или 11 шпилек на кольце. Шпильки сделаны из стальной проволоки диаметром 5 – 6 мм и длиной 30 – 40 см в нерабочем положении ленту наматывают на кольцо

Для измерения небольших расстояний применяют стальные и тесьмяные рулетки длиной 5, 10, 20, 50 м. Деления на рулетках нанесены на одной стороне через 1см и редко через 1 мм. Свернутая рулетка помещается в металлический или пластмассовый корпус.

Компарирование мерных приборов.

Мерные ленты и рулетки перед измерением ими линий должны быть проверены. Данная проверка называется компарированием и состоит в установлении действительной длины мерного прибора путем его сравнения с образцовым прибором, длина которого точно известна.

Для компарирования штриховых лент за образцовый мерный прибор принимают одну из лент, имеющихся на производстве, длину которой выверяют в лаборатории Государственного надзора за стандартами и измерительной техникой Государственного комитета стандартов РФ и пользуются ею при сравнении с рабочими лентами. Компарирование шкаловых лент производят на специальных приборах, называемых стационарными компараторами.

Простейший способ компарирования штриховых лент состоит в следующем. На горизонтальной поверхности, например, на полу, укладывают образцовую ленту. Рядом с ней кладут проверяемую ленту так, чтобы их края касались друг друга, а нулевые штрихи совмещались. Жестко закрепив концы с нулевыми штрихами, ленты натягивают с одинаковой силой и измеряют миллиметровой линейкой величину несовпадения конечных штрихов на других концах лент. Данная величина показывает на сколько миллиметров рабочая лента короче или длиннее образцовой и называется поправкой за компарирование Δℓ.

Длина проверяемой 20-метровой ленты не должна отличаться от длины образцовой ленты более чем на ±2 мм. В противном случае в результаты измерения линий вводят поправки. При этом, выполняя измерения линий рабочей лентой, полагают, что её длина равняется 20 м. Поправки определяют по формуле

где D – длина измеренной линии.

Поправку вычитают из результатов измерения, когда рабочая лента короче образцовой, и прибавляют, когда она длиннее.

Вешение линий

Прямую линию на местности обычно обозначают двумя вехами, установленными на её концах. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то с целью удобства и повышения точности измерения её длины используют дополнительные вехи. Их устанавливают в воображаемой отвесной плоскости, проходящей через данную линию. Эту плоскость называют створом линии. Установка вех в створ данной линии называется вешением

Порядок измерения линий .

Измерение линий на местности штриховыми лентами производят двое рабочих. По направлению измерения один из них считается задним, второй – передним. Ленту аккуратно разматывают с кольца. Её оцифровка должна возрастать по ходу измерения. Для закрепления мерной ленты в створе линии используется 6 шпилек. Перед началом измерения 5 шпилек берет передний мерщик и одну – задний. Задний мерщик совмещает с началом линии нулевой штрих ленты. Используя прорезь в ленте, закрепляет шпилькой её конец рядом с колышком, обозначающим начальную точку линии

Передний мерщик, имея в руке 5 шпилек, по указанию заднего мерщика, встряхнув ленту, натягивает её в створе линии и фиксирует первой шпилькой передний конец ленты. Затем задний мерщик вынимает свою шпильку из земли, вешает её на кольцо, и оба мерщика переносят ленту вперед вдоль линии. Дойдя до воткнутой в землю передним мерщиком шпильки, задний мерщик закрепляет на ней свой конец ленты, а передний, натянув ленту, закрепляет её передний конец следующей шпилькой (рис.). В таком порядке мерщики укладывают ленту в створе линии 5 раз.

После того как передний мерщик зафиксирует пятой шпилькой свой конец ленты, задний мерщик передает ему кольцо с пятью шпильками, которые он собрал в процессе измерения (рис.). Число таких передач (т.е. отрезков по 100 м при длине ленты в 20 м) записывают в журнале измерений. Последний измеряемый остаток линии обычно меньше полной длины ленты. При определении его длины метры и дециметры отсчитывают по ленте, а сантиметры оценивают на глаз (рис.).

Измеренная длина линии D вычисляется по формуле :

D = 100 · a + 20 · b + c,

где a – число передач шпилек;

b – число шпилек у заднего мерщика на кольце;

Для контроля линию измеряют вторично 24-метровой или той же 20-метровой в обратном направлении. За окончательный результат принимают среднее арифметическое из двух измерений, если их расхождение не превышает:

– 1/3000 части от длины линии при благоприятных условиях измерений;

– 1/2000 – средних условиях измерений;

– 1/1000 – неблагоприятных условиях измерений.

Ослабление влияния данных факторов на точность измерений достигается более тщательным вешением линий, использованием динамометров для натяжения лент, введением поправок в измеренные длины, проведением контрольных измерений и т. п.

На точность измерения длин мерной лентой большое влияние оказывают условия местности, характер грунта и растительного покрова. Поэтому в зависимости от рельефа и условий измерений условно различают три класса местности:

I класс – местность, благоприятная для измерений (ровная поверхность с твердым грунтом);

II класс – местность со средними условиями для измерений (холмистая поверхность со слабым грунтом);

III класс – местность, неблагоприятная для измерений (сильно пересеченная, заросшая кустарником местность с кочками и выемками, с песчаной или заболоченной почвой).

Практикой установлено, что относительные погрешности измерения линий штриховыми мерными лентами не должны превышать: на местности I класса – 1:3000, II класса – 1:2 000 и
III класса – 1:1 000.

Длинномер

Длинномер относят к подвесным мерным приборам. В длинномере стальную проволоку натягивают между двумя фиксированными на местности точками. По проволоке в процессе измерения прокатывают устройство, основными элементами которого являются мерный диск и счетный механизм, позволяющий установить количество оборотов диска на прокатываемом отрезке проволоки

Схема измерения расстояния длинномером.
1 – длинномер; 2 – проволока; 3 – шкалы; 4 – динамометр; 5 – груз; 6 – стремя;
7 – штативы; 8 – раздвижные стойки-упоры; 9 – оптический центрир

Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.

Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.

Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.

Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.

Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.

Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.

Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:

Здесь l – длина ленты при температуре t; l₀ – номинальная длина; Dl – поправка к номинальной длине при температуре компарирования t₀ ; a – температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.

Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D – вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D₁, то есть в створ точек C и B. Затем из точки С веху переносят в точку С₁ и так далее до тех пор, когда обе вехи окажутся в створе AB.

Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n – число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).

Длину измеряют дважды – в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях – 1/1000). За окончательное значение принимают среднее.

Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.

Поправка за компарирование определяется по формуле

где Dl – отличие длины ленты от 20 м и n – число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.

Поправка за температуру определяется по формуле

где a – термический коэффициент расширения (для стали a = 0,0000125); t и t₀ – температура ленты во время измерений и при компарировании. Поправку D_t учитывают, если ½t–t₀½>10°.

Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D

где n – угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где

D_n = d – D = D (cosn – 1) = -2D sin 2 . (8.3)

По формуле (8.3) составляют таблицы, облегчающие вычисления.

Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.

Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.

Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.

Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами – глазным 1 и предметным 4.

Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона

Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 – 30¢.

Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.

Точность измерений лентой в разных условиях различна и зависит от многих причин – неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.

Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.

Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта d_i определяют по формуле

где П и З – передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).

Если линия имеет наклон, необходимо учесть поправку

,

где h – превышение между концами пролёта, измеряемое нивелиром.

Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 – 1:10000.

Одним из основных видов измерений в геодезическом производстве считаются линейные измерения. Измеряют в пространстве и на плоскости, на физической поверхности и в ее недрах. Меряют всевозможные линейные размеры:

• длины и ширины предметов и конструкций;
• глубины и высоты подземных и наземных сооружений;
• пролеты внутри объектов и сечения горных выработок;
• межосевые размеры и отклонения от них;
• всевозможные геометрические параметры.

Также замеряют расстояния:

• между известными и неизвестными точками;
• конкретной точкой и плоскостью;
• двумя плоскостями;
• линией и плоскостью;
• разными линиями.

В геодезической области линейные измерения осуществляют при выполнении:

• измерения высоты инструмента на точке стояния прибора;
• определения горизонтальных проложений и длин линий между геодезическими пунктами и измеряемыми предметами;
• построения и сгущения геодезических сетей опорного и съемочного обоснований;
• подготовки исходных данных во всевозможных геодезических разбивочных работах в строительстве;
• и выверке монтажного и технологического оборудования;
• геодезического контроля и исполнительных съемок;
• всех видов геодезических съемок и других работ, связанных с геометрией пространства.

Способы и приборы в геодезических измерениях расстояний

Все линейные измерения в геодезии исполняют двумя способами:

• прямым методом, заключающимся в непосредственном определении (снятии отсчетов) измеряемого размера или расстояния;
• косвенным методом, представляющим нахождение измеряемой величины через функциональные зависимости по формулам.

Небольшие расстояния измеряют металлическими рулетками и лентами разной длины, лазерными и оптическими дальномерами.

Расстояния значительной длины измеряют с использованием современных приборов таких, как радиодальномеры, электронные тахеометры, лазерные свето-дальномеры, способные измерять километровые расстояния.

Мерные ленты и рулетки

Для выполнения линейных измерений, так же как и для угловых, нормативными документами для различного вида съемок или работ предусматриваются определенные требования. Этими требованиями всегда являются измеряемая точность приборов и относительные погрешности измерений. В зависимости от них и выбираются инструменты по измерению длин линий.

Мерные ленты и рулетки применяются при непосредственном измерении расстояний. Рулетки бывают разной длины (3, 5, 10, 30, 50 метров) и изготовлены из разных материалов:

• тесьмяные;
• углеродистой стали;
• нержавеющей стали;
• фиберглассовые;
• стальные с нейлоновым покрытием.

Тесьмяные рулетки используют для мало точных измерений для замеров объемов выполненных работ рулеточными замерами подземных коммуникаций, проведения открытых и подземных горных выработок, их сечений. Такая рулетка состоит из измерительной тканевой ленты с пропиткой и вплетенными в нее металлическими нитями. Она изготавливается в пластмассовом корпусе с намотанной на ось лентой.

Рулетки металлические, с нержавеющей стали или стальными каркасами с полимерным покрытием применяют при непосредственных измерениях расстояний. Они при профессиональном использовании должны быть прокомпарированны, то есть сравнимы с официальным эталоном определенной длины компаратором. После прохождения этой поверки по каждой рулетке составляется паспорт, в котором указываются истинные значения отрезков и длины рулетки, а так же поправок, подлежащих обязательному введению в результаты измерений длин. Согласно, государственных стандартов отклонение при взятии отсчетов в стальных рулетках должно быть не более 2 мм и точность в измерениях ими имеет относительную погрешность в пределах от одной двухтысячной (1/2000) до одной десяти тысячной (1/10000) от соответствующих значений длины. В комплекте с рулетками при измерительном процессе используют специальные приборы – пружинные динамометры. Они позволяют каждый раз производить снятие отсчетов по шкале рулетки при одинаковом ее натяжении, равном усилию порядка десяти килограмм.

Мерные ленты в настоящее время на практике используются, наверное, очень редко. Они бывают со шкалами на концах ленты и без них, и имеют маркировку ЛШЗ (лента шкаловая землемерная), и ЛЗ (лента земельная). В их комплект входят:

• собственно сама лента, намотанная на стальное кольцо и с ручками по краям, длина лент бывает различная, 20, 24 и 50 метров;
• и наборы по шесть или одиннадцать штук шпилек, представляющие собой металлические стержни (длиной 300-400 мм, диаметром 5-6 мм) с загнутым с одной стороны кольцом диаметром 70-80 мм.

Базисный прибор и длиномеры

Для некоторых высокоточных линейных измерений применяли приборы, состоящие не из металлической полосы или ленты, а из проволоки специального металлического сплава. К таким приборам, безусловно, относится так называемый базисный прибор. Ранее, в геодезическом и маркшейдерском производстве использовались также автоматические проволочные длиномеры. Каждый из них использовался для конкретных видов работ.

• двадцати четырех метровые отрезки инварной проволоки, в количестве от трех до восьми штук, в зависимости от марки прибора (БП-1, БП-2, БП-3);
• два блока с грузами, в виде десяти килограммовых гирь, через которые подвешивается и натягивается мерная проволока;
• штативы с целью фиксации инварной проволоки в измеряемом створе;
• трегеры с оптическими центрирами, теодолиты, нивелиры, термометры и другое вспомогательное оборудование.

В маркшейдерской практике для измерения глубины вертикальных шахтных стволов применялись автоматические длиномеры ДА-2, состоящие:

• из единого корпуса, со встроенной лебедкой, через которую опускается в шахтный ствол мерная проволока;
• и мерного диска со счетчиком оборотов и шкалой на реборде.

В поверхностной полигонометрии использовались автоматические длиномеры марки АД-1м. В их состав входили: проволока, проходящая через длиномер с мерным диском, со считываемым устройством, направляющими роликами и тормозным механизмом.

Оптический дальномер

Применению оптического способа определения расстояний между прибором и точками измерений способствовали конструктивные особенности оптических теодолитов и тахеометров. Известный всем геодезистам и маркшейдерам способ определения расстояния нитяным дальномером с постоянным параллактическим углом основан на тригонометрической зависимости:

где b – измеряемый переменный базис (длина);

φ – постоянный параллактический угол;

L – измеряемая длина.

Технически механизм этого метода выглядит в снятии отсчетов по дальномерным нитям сетки нитей, наблюдаемым в поле зрения зрительной трубы, с соответствующей шкалы на поверхности нивелирных реек. Относительная ошибка измерений линий таким способом составляет в районе одной четырехсотой (1/400) длины. Его используют при выполнении, как одиночных определений расстояния, так и при популярной тахеометрической съемке.

Электронные тахеометры, свето-дальномеры и лазерные рулетки

В основе измерения расстояний профессиональными лазерными рулетками, свето-дальномерами, которые применяются и в современных конструкциях электронных тахеометров, заложены три принципа:

• импульсный;
• фазовый;
• комбинированный (импульсно-фазовый).

Импульсный метод состоит в определении измеряемой длины через нахождение времени прохождения сигналов инфракрасного лазерного излучения от источника импульса до объекта и обратно. В фазовом методе длины сторон измеряются через определение разности фаз переданного и получаемого сигналов. Оба этих принципа дают достаточно высокую точность на разных расстояниях от приборов.

В современных тахеометрах используется также комбинированный метод, заключающийся в фазовом способе определения временного промежутка при импульсном излучении сигнала. Нахождения расстояний с их помощью может осуществляться в трех режимах:

• безотражательном;
• на светоотражательную пленку;
• на стандартные призмы.

Для безотражательного способа нахождения длин (горизонтальных проложений) и с применением светоотражательных пленок для расстояний от 0,3 м до 500 м электронные тахеометры дают паспортную точность ± 2-3 мм. При наведении на отражательные конструкции призм на расстояния до пяти километров точность определения увеличивается дополнительно до 2ppm на каждый дополнительный километр измерений.

Лазерные рулетки с такой высокой точностью позволяют очень разнообразно использовать их в строительных и отделочных работах, с учетом наличия в них дополнительных опций по определению площадей, объемов и других.

Радиодальномеры

Радиодальномеры, которые применяются в геодезии, имеют практически одну принципиальную схему. Отличаются они между собой только конструкцией исполнения. В них используется принцип приема передачи ультракоротких волн на разных частотах от геодезического прибора на одной несущей частоте до приемо-передатчика и в обратном направлении на другой измерительной частоте. Расстояние между прибором и приемочной станцией определяется по разностям фаз, измеряемых на нескольких различных фиксированных частотах. Достоинствами такого способа измерений считаются значительная дальность применения и возможность работы при любой непогоде независимо от видимости. К недостаткам можно отнести громоздкость и тяжесть измеряемого оборудования и сравнительно большая и постоянная составляющая погрешности измерений (20-30 мм).

Целью линейных измерений является определение горизонтальных расстояний (проложений) между точками местности. Длины линий местности в геодезии измеряют непосредственным либо косвенным способами; каждому из этих способов присущи свои приборы и методы измерений.

Непосредственный способ основан на непосредственном измерении линий местности механическими линейными приборами, к которым относятся мерные ленты, рулетки и проволоки. Процесс измерения длин линий непосредственным способом состоит в последовательном откладывании мерного прибора в створе линии.

При косвенном способе длина линии определяется как функция установленных геометрических или физических соотношений. Геометрические соотношения используют для аналитических вычислений искомых расстояний по измеренным базисам и углам, а также в оптических дальномерах. Физические соотношения для измерения расстояний положены в основу конструкции электрофизических приборов – светодальномеров и радиодальномеров.

Для непосредственного измерения линий применяются следующие приборы: мерные ленты длиной 20 и 24, реже 50 и 100 м. Мерные ленты изготавливают из стали или инвара (сплав 64 % железа, 35,5 % никеля и 0,5 % различных добавок, обладающего малым температурным коэффициентом линейного расширения). По конструкции различают штриховые и шкаловые ленты.

– Штриховая лента представляет собой стальную полосу длиной 20 или 24 м, шириной 15-20 мм и толщиной 0,3-0,4 мм. За длину ленты принимается расстояние между штрихами, нанесенными напротив середины закруглений специальных вырезов, в которые вставляются металлические заостренные шпильки для фиксации концов ленты на земной поверхности в процессе измерений (рисунок 14).

– 20-метровая штриховая лента разделена на метры, полуметры и дециметры. Метровые деления отмечены с обеих сторон полотна овальными пластинками, на которых выдавлены порядковые номера метров; дециметровые деления обозначены отверстиями в полотне ленты, а полуметры – круглыми заклепками с шайбами. Отрезки линий менее дециметра оцениваются по ленте на глаз с точностью до 1 см. В нерабочем положении лента наматывается на специальную металлическую кольцевую оправу и закрепляется винтом. К ленте прилагается комплект из 6 или 11 шпилек на проволочном кольце.

Рисунок 14 – Штриховая мерная лента

– Шкаловая лента,представляет собой сплошную полосу, на концах которой имеются шкалы длиной по 10 см с миллиметровыми делениями (рисунок 15) разбивка на метровые и дециметровые отрезки на ленте отсутствует. За длину ленты принимается расстояние между нулевыми делениями шкал.

Механические приборы для непосредственного измерения

Способы измерения длин линий

Измерение длины линий оптическими дальномерами.

Определение горизонтальныхпроложений наклонных линий.

Вешение и измерение линий мерной лентой, точность измерения.

Способы измерения длин линий.

ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ

3.2 Механические приборы для непосредственного измерения линий, их

3.6 Косвенные способы измерения расстояний.

Целью линейных измерений является определение горизонтальных расстояний (проложений) между точками местности. Длины линий местности в геодезии измеряют непосредственным либо косвенным способами; каждому из этих способов присущи свои приборы и методы измерений.

Непосредственный способ основан на непосредственном измерении линий местности механическими линейными приборами, к которым относятся мерные ленты, рулетки и проволоки. Процесс измерения длин линий непосредственным способом состоит в последовательном откладывании мерного прибора в створе линии.

При косвенном способе длина линии определяется как функция установленных геометрических или физических соотношений. Геометрические соотношения используют для аналитических вычислений искомых расстояний по измеренным базисам и углам, а также в оптических дальномерах. Физические соотношения для измерения расстояний положены в основу конструкции электрофизических приборов – светодальномеров и радиодальномеров.

Для непосредственного измерения линий применяются следующие приборы: мерные ленты длиной 20 и 24, реже 50 и 100 м. Мерные ленты изготавливают из стали или инвара (сплав 64 % железа, 35,5 % никеля и 0,5 % различных добавок, обладающего малым температурным коэффициентом линейного расширения). По конструкции различают штриховые и шкаловые ленты.

– Штриховая лента представляет собой стальную полосу длиной 20 или 24 м, шириной 15-20 мм и толщиной 0,3-0,4 мм. За длину ленты принимается расстояние между штрихами, нанесенными напротив середины закруглений специальных вырезов, в которые вставляются металлические заостренные шпильки для фиксации концов ленты на земной поверхности в процессе измерений (рисунок 14).

– 20-метровая штриховая лента разделена на метры, полуметры и дециметры. Метровые деления отмечены с обеих сторон полотна овальными пластинками, на которых выдавлены порядковые номера метров; дециметровые деления обозначены отверстиями в полотне ленты, а полуметры – круглыми заклепками с шайбами. Отрезки линий менее дециметра оцениваются по ленте на глаз с точностью до 1 см. В нерабочем положении лента наматывается на специальную металлическую кольцевую оправу и закрепляется винтом. К ленте прилагается комплект из 6 или 11 шпилек на проволочном кольце.

Рисунок 14 – Штриховая мерная лента

– Шкаловая лента,представляет собой сплошную полосу, на концах которой имеются шкалы длиной по 10 см с миллиметровыми делениями (рисунок 15) разбивка на метровые и дециметровые отрезки на ленте отсутствует. За длину ленты принимается расстояние между нулевыми делениями шкал.

Читайте также:

  

• Орфоэпические нормы русского языка кратко таблица

  

• Уравнение времени это кратко

  

• Преобразование географической среды кратко

  

• Классификация чувствительных элементов средств обнаружения кратко

  

• Мясковский 6 симфония кратко