Содержание
- Практическая работа №1 Решение задач на масштабы
- МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
- Практическая работа №1
Практическая работа №1 Решение задач на масштабы
Масштаб — это отношение длины линии на карте, плане (чертеже) Sp к длине горизонтального приложения соответствующей линии в натуре (на местности) Sm.
Численный масштаб — 1/ М, правильная дробь, у которой числитель равен 1, а знаменатель М показывает во сколько раз уменьшены линии местности по сравнению с планом.
Например, масштаб 1:10000 означает, что все линии местности уменьшены в 10000 раз, т.е. 1 см плана соответствует 10000 см на местности
или 1 см плана = 100 м на местности,
или 1 мм плана = 10 м на местности.
Следовательно, зная длину отрезка Sp плана по формуле Sm=Sp*M можно вычислить длину линии на местности или по формуле Sp= Sm:M определить длину отрезка на плане.
Например, длина линии на местности 252 м; масштаб плана 1:10000. Тогда длина линии на плане Бр=252м : 10000=0,0252м = 25,2мм.
И обратно, длина отрезка на плане равна 8,5 мм; масштаб плана 1:5000. Требуется определить длину линии местности. Она будет 8,5 мм * 5000 = 42,5м.
Задача №1 Вычислите длину линии на местности Sm, для данных, приведенных в таблице 1. Результаты запишите в соответствующую графу таблицы 1.
| Таблица 1. | |||||
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:10000 | 62,5 | 1:1000 | |||
| 1:25000 | 20,2 | 1:500 | |||
| 1:5000 | 12,5 | 1:2000 | |||
| 1:50000 | 6,2 | 1:5000 |
| Таблица 2. | |||||
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:2000 | 80,4 | 1:50000 | |||
| 1:5000 | 380,5 | 1:1000 | |||
| 1:10000 | 1:500 | ||||
| 1:25000 | 1:2000 |
Часто в геодезической практике приходится определять масштабы аэроснимков. Для этого измеряют длину отрезка на аэроснимке и длину горизонтального проложения этой линии на местности. Затем, используя определение масштаба, вычисляют масштаб.
Например: длина отрезка на аэроснимке 2.21 см.; длина горизонтального проложения этой линии на местности 428,6 м.
Тогда, согласно определению:
Задача №2Определите масштабы аэроснимков, по данным приведенным в таблице 3. результаты записать в соответствующую графу таблицы 3
| №п/п | Длина горизонтального приложения на местности м | Длина отрезка на аэроснимке | Отношение в соответствующих единицах | Масштаб аэроснимка |
| 625 м | 62,5 мм | 62,5 мм /625000мм | 1:10000 | |
| 525 м | 5,25 см | |||
| 125,5 м | 2,51 см | |||
| 62,2 м | 31,1 см |
Длины линий на местности, соответствующие 0,1 мм карты (плана) называется точностью масштаба — tm. Это величина, характеризующая точность определения длин линий по карте (плану). Например: точность масштаба 1:25000 равна 2,5 м.
Расчет можно вести следующим образом:
или to =0,1мм* 25000=2,5 м.
Задача №3
а) Определите точность масштабов:
б) Точность масштаба карты (плана) равна:
tm1=0,5м; t2=0,05M; t3=___ ___; t4=_______;
Определите масштаб карты (плана) .
1/М1=______; 1/М2=_______; 1 /МЗ=_______; 1/М4=_______;
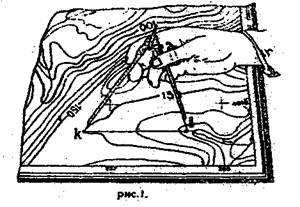
Задача №4 На карте масштаба 1:10000 (рис. 1) показан раствор измерителя, равный расстоянию между двумя точками карты KL. Используя приведенный ниже график линейного масштаба (рис.2), определите длины горизонтальных приложений линий местности для всех вариантов.
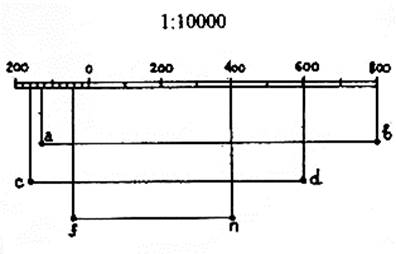
Задача №5 На графике поперечного масштаба (рис.3) с основанием равным 2 см., утолщенными линиями с номерами, обозначен раствор измерителя, равный расстоянию между двумя точками карты
Определите длины горизонтальных проложений линий местности для следующих вариантов:
| I вариант, масштаб 1:10000 | II вариант, масштаб 1:5000 |
| S1= | S1= |
| S2= | S2= |
| S5= | S5= |
| S= | S= |
| Ш вариант, масштаб 1:2000 S1= | IV вариант, масштаб 1: S1= |
| S2= | S2 = |
| S5= | S5 = |
| S= | S= |
Указание: в начале определите расстояния на местности (в соответствующем масштабе) для отрезков 0-2; а1в1; а2в2; аЗвЗ.
Задача №6 Постройте диаграмму масштаба 1:2000 на чертежной бумаге с основанием 2,5 см; число делений по основанию и по высоте принять равным 10 (n=m=10). Подпишите деления по основанию и высоте (через одно). Диаграмму приклеить, на оставленное ниже место.
Поделиться с друзьями:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.009 сек. —>
Источник
МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
РЕШЕНИЕ ГЕОДЕЗИЧЕСКИХ ЗАДАЧ
НА ТОПОГРАФИЧЕСКИХ ПЛАНАХ И КАРТАХ
Приведены основные геодезические задачи, решаемые на топографических картах и планах. Решение типовых задач дано с подробными пояснениями.
Вариантный подбор задач дает возможность проводить проверку знаний студентов. Ответы на большинство задач даны в конце методических указаний.
Предназначены для студентов специальностей СЖД, МТ, ВиВ, ПГС, ПТ и УПП всех форм обучения.
МАСШТАБЫ. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ НА КАРТЕ
При изображении участков земной поверхности на плане их размеры уменьшают в некоторое число раз. Отношение длины линии на плане к длине горизонтальной проекции соответствующей линии местности называют масштабом плана. Масштаб, выраженный дробью, у которой числитель равен единице, а знаменатель показывает, во сколько раз уменьшены горизонтальные расстояния местности при нанесении их на план, называется численным, например 
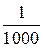
Чем больше знаменатель численного масштаба, тем масштаб мельче, чем знаменатель меньше, тем масштаб крупнее.
Масштаб 1 : 2 000 показывает, что 1 см на плане соответствует 20 м на местности (так как 2 000 см = 20 м).
С применением масштабов можно решать различные задачи.
Задача № 1. На плане масштаба 1 : 500 измерено расстояние а = = 56,5 мм. Определить длину d горизонтального проложения данной линии на местности.
Решение. Вычисление производится по формуле
где М – знаменатель численного масштаба.
Находим d = 56,5 · 500 = 28 250 мм = 28,25 м.
Задача № 2. Дано горизонтальное проложение линии на местности d = 214 м. Определить длину соответствующего отрезка на плане масштаба 1 : 2 000.
Решение. Используя формулу, приведенную в предыдущей задаче, получим:
а = d/М = 214/2 000 = 0,107 м = 10,7 см.
Задача № 3. Определить масштаб карты в пять раз крупнее масштаба 1 : 25 000.
Решение. Зная, что чем меньше знаменатель численного масштаба, тем масштаб крупнее, разделим знаменатель заданного масштаба на 5 и получим масштаб карты 1 : 5000.
Следующие задачи предлагается решить самостоятельно (ответы приведены в конце методических указаний).
Задача № 4. На плане масштаба 1 : 2 000 измерен отрезок длиной 4,3 см. Определить длину горизонтального проложения данного отрезка на местности.
Задача № 5. Какой отрезок следует отложить на плане масштаба 1 : 5 000, если горизонтальное расстояние на местности равно 850 м?
Задача № 6. Определить масштаб карты в два раза мельче масштаба 1 : 25 000.
При определении горизонтального проложения между двумя точками вначале необходимо измерить это расстояние на карте, а потом, используя численный масштаб карты, вычислить значение горизонтального проложения на местности. Чтобы не делать вычислений, связанных с использованием численного масштаба, под южной рамкой карты помещен графический (линейный) масштаб. В раствор циркуля берут с карты определяемое расстояние, прикладывают его к линейному масштабу и читают, какому расстоянию на местности оно соответствует. На рис. 1 изображен линейный масштаб для численного 1 : 10 000 и показаны расстояния 500 и 540 м.
Рис. 1. Определение расстояния по линейному масштабу
Задача № 7. Определить с помощью линейного масштаба на карте У-34-37-В-в-4 (см. приложение) расстояние между точкой с отметкой 151,8 м (квадрат 65×13) и точкой с отметкой 140,9 м (квадрат 65×13).
Для более точного измерения и откладывания расстояний на карте используют поперечный масштаб, который обычно выгравирован на металлических линейках, называемых масштабными.
Для построения поперечного масштаба на горизонтальной прямой откладывают несколько раз одинаковый отрезок, называемый основанием масштаба (рис. 2). Левое основание делят на 10 равных частей (малые деления). Из всех полученных точек восставляют перпендикуляры. На перпендикулярах также откладывают по 10 равных частей и через точки отложения проводят линии, параллельные основанию. Затем через деления левого основания проводят наклонные линии, как показано на рис. 2.
Рис. 2. Определение расстояний по поперечному масштабу
Из подобия треугольников BDE и Bde следует Вd/ВD = de/DE, или de = Bd · DE/BD. Но DE =АВ/10, поэтому Bd = ВD/10. Следовательно, de = АВ/100, т. е. наименьшее деление поперечного масштаба равно 0,01 основания. Эта величина называется предельной графической точностью поперечного масштаба.
Если основание масштаба равно 2 см, то поперечный масштаб носит название нормального поперечного масштаба.
Для определения расстояния между двумя точками на карте берут это расстояние в раствор циркуля-измерителя и переносят его на нижнюю линию поперечного масштаба. Если между иглами измерителя вмещается целое число оснований и малых делений, то отсчитывают расстояние. Если же левая игла измерителя попадает между двумя наклонными линиями малого деления, то измеритель перемещают вверх, параллельно основанию, пока левая игла не будет точно лежать на наклонной линии. Правая игла при этом должна располагаться на одной из вертикальных линий поперечного масштаба.
Задача № 8. Определить по схеме нормального поперечного масштаба (рис. 2) длину отрезка 1, измеренного на карте масштаба 1 : 10 000.
Решение. По численному масштабу карты определяем, что основанию (AB)поперечного масштаба 2 см соответствует расстояние на местности, равное 200 м. Левое основание разделено на 10 равных делений. Следовательно, малому делению (DE) соответствует расстояние в 20 м. Наименьшее деление поперечного масштаба (de),т. е. предельная графическая точность масштаба, составит 0,1 малого деления и равна 2 м. При определении длины отрезка 1 имеем: 2 · 200м + 6 · 20 м + 3 · 2 м = 526 м.
Задача № 9.Определить по нормальному поперечному масштабу на рис. 2 длину отрезка 2, измеренного на плане масштаба 1 : 2 000.
Решение. По численному масштабу плана определяем: основанию 2 см соответствует 40 м; малому делению – 4 м; наименьшему делению – 0,4 м. Искомая длина составит (см. рис. 2): вправо от B одно основание, то есть 40 м; влево от B три малых деления по 4 м, то есть 12 м; вверх по наклонной линии поднялись на 5 наименьших делений по 0,4 м каждое, чему соответствует 2 м. Получаем: 40 + 12 + 2 = 54 м.
Задача № 10. Определить по схеме нормального поперечного масштаба длины отрезков 1 и 3 для карты масштаба 1 : 25 000.
Задача № 11. Определить по схеме нормального поперечного масштаба длины отрезков 2 и 4 для плана масштаба 1 : 5 000.

Для измерения расстояния по извилистым дорогам, рекам и другим кривым линиям существуют специальные приборы, которые называют курвиметрами (рис. 3). В основании курвиметр имеет колесико, длина окружности которого известна. Колесиком прибора проводят по измеряемой линии. Вращение колесика передается на стрелку, указывающую на шкале циферблата измеренное расстояние. Для приближенного определения длины кривой линии (при отсутствии курвиметра) можно разбить ее на ряд отрезков, близких к прямым, и измерить ее как сумму прямых отрезков.
Рис. 3. Курвиметр
Задача № 13. Определить криволинейное расстояние по улучшенной грунтовой дороге (карта У-34-37-В-в-4) от населенного пункта Михалино до пересечения ее с шоссе (отметка 144,0 м, квадрат 65×14).
Источник
Практическая работа №1
на тему: «Масштабы топографических карт и планов»
ТЕМА: Масштабы топографических карт, планов и чертежей.
ЦЕЛЬ: Изучить масштаб и формы его выражения. Научиться измерять и откладывать длины отрезков на картах и планах. Получить навыки решения задач на масштабы.
В результате изучения темы студент должен:
- формы записи масштаба на карте, плане;
- определение масштаба;
- пользоваться графическим масштабом;
- выполнять метрические и угловые измерения на карте.
- Дать определение плана.
- Дать определение карты.
- Дать определение масштаба.
- Виды масштаба: численный, линейный и поперечный.
- Дать определение точности масштаба.
Задание 1. Вычислите длину линии на местности Sm, для данных, приведенных в таблице 1. Результаты запишите в соответствующую графу таблицы 1.
| Масштаб карты | Длина отрезка на карте (Sp), мм | Длина линии на местности Sm, м | Масштаб карты | Длина отрезка на плане Sp, мм | Длина линии на местности Sm, м |
| 1: 10000 | 62, 5 | 1: 1000 | |||
| 1: 25000 | 20, 2 | 1: 500 | |||
| 1: 5000 | 12, 5 | 1: 2000 | |||
| 1: 50000 | 6, 2 | 1: 5000 |
Задание 2.Вычислите длину линии на плане Sр для данных, приведенных в таблице 2. Результаты запишите в соответствующую графу таблицы 2.
| Масштаб карты | Длина отрезка на карте (Sp), мм | Длина линии на местности (Sm), м | Масштаб карты | Длина отрезка на плане (Sp), мм | Длина линии на местности (Sm), м |
| 1: 2000 | 80, 4 | 1: 50000 | |||
| 1: 5000 | 380, 5 | 1: 1000 | |||
| 1: 10000 | 1: 500 | ||||
| 1: 25000 | 1: 2000 |
Задание 3.Определите масштабы аэроснимков, по данным, приведенным в таблице 3. Результаты запишите в соответствующую графу таблицы 3.
| №п/п | Длина горизонтального проложения на местности (Sm), м | Длина отрезка на аэроснимке (Sp) | Отношение в соответствующих единицах | Масштаб аэроснимка |
| 625 м | 62, 5 мм | 62, 5 мм /625000мм | 1: 10000 | |
| 525 м | 5, 25 см | |||
| 125, 5 м | 2, 51 см | |||
| 62, 2 м | 31, 1 см |
Задание 4.Определите точность масштабов:
Задание 5. Используя приведенный ниже график линейного масштаба (рис.1), определите длины горизонтальных приложений линий местности для всех вариантов.
Рисунок 1 – Линейный масштаб
Задание 6. На графике поперечного масштаба с основанием равным 2 см утолщенными линиями с номерами, обозначен раствор измерителя, равный расстоянию между двумя точками карты. Определить длину линий для масштабов указанных ниже.
1 — масштаб 1: 10000 2 — масштаб 1: 5000
3 — масштаб 1: 2000 4 — масштаб 1:
Подпись студента_______ Подпись преподавателя____________
Источник
Лабораторная работа №1
Тема: Построение линейного масштаба.
Цель: научить студентов строить линейный масштаб.
Методическое обеспечение: масштабные линейки, циркуль-измеритель, чертежные принадлежности и лист формата А4, учебные геодезические карты масштабов 1:50000; 1:25000; 1:10000.
Задание
Задание 1. Работа с численными масштабами:
А). Вычислить длины линий на плане в сантиметрах, по их длинам на местности в метрах.
Б). При помощи калькулятора вычислить длины линий на местности в метрах.
Задание 2. Построение графических масштабов:
Построить линейный масштаб с основанием l = 2 см(5см), т = 10.
Задание 3. По данным задания 1, пользуясь построенными графическими масштабами и измерителем, отложить на бумаге длины линий на линейном масштабе.
Ход работы:
1.Входящий контроль:
1.1. Численный масштаб 1:100. Сколько метров в 1 см?
1.2. Численный масштаб 1:2000. Сколько метров в 10 см?
1.3. Численный масштаб 1:5000. Сколько метров в 1 мм?
2.Последовательность выполнения практической работы:
Работа с численными масштабами
2.1. Вычислить длины линий на плане в сантиметрах, по их длинам на местности в метрах. Исходные данные см. таблицу №1.
Таблица №1
|
№ варианта |
Длина линии на местности, м |
Масштабы планов 1: М |
|
1 |
128,4 |
1:2 000 |
|
2 |
24,8 |
1:2 000 |
|
3 |
47,8 |
1:2 000 |
|
4 |
2456,5 |
1:50 000 |
|
5 |
84,0 |
1:5 000 |
|
6 |
49,5 |
1:5 000 |
|
7 |
850,0 |
1:25 000 |
|
8 |
1277,5 |
1:50 000 |
|
9 |
425,0 |
1:25 000 |
|
10 |
683,7 |
1:10 000 |
|
11 |
234,0 |
1:5 000 |
|
12 |
343,8 |
1:10 000 |
|
13 |
193,4 |
1:5 000 |
|
14 |
146,2 |
1:2 000 |
|
15 |
286,9 |
1:2 000 |
|
16 |
43,4 |
1:500 |
|
17 |
722,9 |
1:1 000 |
|
18 |
11,1 |
1:200 |
|
19 |
18,3 |
1:100 |
|
20 |
75,65 |
1:500 |
|
21 |
65,1 |
1:1 000 |
|
22 |
108,4 |
1:2 000 |
|
23 |
171,5 |
1:5 000 |
|
24 |
327,0 |
1:10 000 |
|
25 |
521,7 |
1:5 000 |
Чтобы получить длину линии на плане в сантиметрах, надо ее длину на местности в метрах разделить на знаменатель численного масштаба плана М, уменьшенный в 100 раз.
П р и мер.
Длина линии на местности d = 456,5 м, масштаб плана 1:5000. Длина этой линии на плане равна:
2.2. При помощи калькулятора вычислить длины линий на местности в метрах. Исходные данные см. таблицу №2.
Таблица №2
|
№ варианта |
Длина линий на плане, см |
Масштабы планов 1: М |
|
1 |
7,28 |
1:5 000 |
|
2 |
5,25 |
1:5 000 |
|
3 |
8,45 |
1:1 000 |
|
4 |
14,52 |
1:500 |
|
5 |
12,43 |
1:1 000 |
|
6 |
3,51 |
1:2 000 |
|
7 |
10,6 |
1:2 000 |
|
8 |
6,2 |
1:5 000 |
|
9 |
10,7 |
1: 200 |
|
10 |
10,4 |
1:5 000 |
|
11 |
7,54 |
1:10 000 |
|
12 |
5,9 |
1:25 000 |
|
13 |
1,8 |
1:50 000 |
|
14 |
2,5 |
1:5 000 |
|
15 |
4,7 |
1:5 000 |
|
16 |
14,1 |
1:1 000 |
|
17 |
9,9 |
1:100 |
|
18 |
11,1 |
1:2 000 |
|
19 |
8,3 |
1:25 000 |
|
20 |
15,65 |
1:5 000 |
|
21 |
8,34 |
1:2 000 |
|
22 |
11,32 |
1:25 000 |
|
23 |
5,83 |
1:2 000 |
|
24 |
6,2 |
1:1 000 |
|
25 |
9,7 |
1:2 000 |
Чтобы получить длину линии на местности в метрах, нужно ее длину на плане в сантиметрах умножить на знаменатель масштаба плана и результат разделить на 100 (отделить запятой два знака справа налево).
Пример.
l = 17,28 см, масштаб 1:2000. Длина этой линии на местности равна:
d = (l*М) : 100 = 17,28 * 2000 : 100 =345,60 м.
Построение графических масштабов:
2.3. Построить линейный масштаб с основанием l = 2 см (четные варианты) и l =5см (нечетные варианты), т = 10.
Пример.
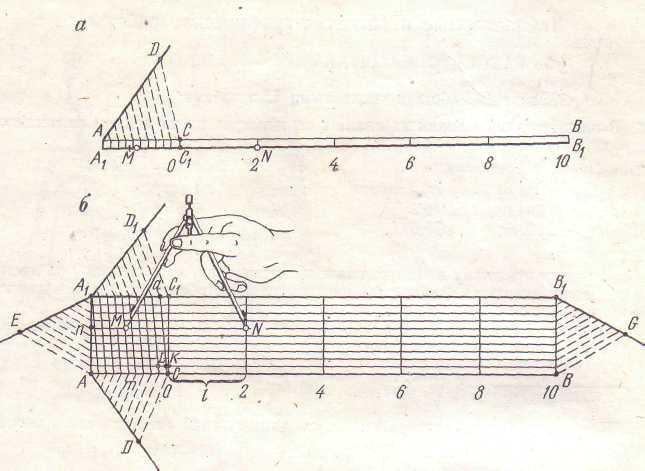
На листе чертежной бумаги (рис. 1, а) прочерчены две параллельные прямые (для наглядности), на которых измерителем отложено 6 отрезков, равных по длине заданному основанию l = 2 см. Эти отрезки называют большими делениями масштаба. Левое основание (большое деление) АС разделено на 10 малых делений длиной по 2 мм.
Для большей точности разделения использован способ проведения параллельных линий при помощи треугольника и линейки. Под произвольным углом к линии АС проводят линию АD, на ней последовательно от точки А откладывают 10 равных отрезков длиною несколько более 2 мм, отмечая полученные точки уколом. Треугольник одним катетом прикладывают к линии DС, к другому его катету прикладывают линейку. Треугольник перемещают вдоль линейки и, проводя линии через отмеченные течки на отрезке АD, получают соответствующие точки на АС. Масштаб вычерчен тушью.
Рис. 1. Построение графических масштабов:
а — линейного
П р и м е р. На плане масштаба I : 2000 отложить линию длиной 52,4 м.
2.4. По линейному масштабу (см. рис. 1, а) расстояние между иголками измерителя MN равно одному большому и 5,6 малого деления, при этом 0,6 малого деления взято на глаз.
3.Выходящий контроль:
3.1. Дать понятие численного масштаба.
3.2. Дать понятие линейного масштаба.
3.3. Что называется точностью масштаба.
4.Защита работы: отчет и контрольные вопросы.
Литература
-
Поклад Г.Г. Геодезия / Г.Г.Поклад. – М.: Недра,1988. – с. 33.
4
8.1. Измерение длин линий мерными лентами и рулетками
Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.
Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.
Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.
Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.
Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.
Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.
Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:
l = l0 + Dl + a l0 (t– t0). (8.1)
Здесь l – длина ленты при температуре t; l0 – номинальная длина; Dl – поправка к номинальной длине при температуре компарирования t0 ; a – температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.
Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.
|
|
Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане). |
Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D – вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D1, то есть в створ точек C и B. Затем из точки С веху переносят в точку С1 и так далее до тех пор, когда обе вехи окажутся в створе AB.
Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n – число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).
Длину измеряют дважды – в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях – 1/1000). За окончательное значение принимают среднее.
Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.
Поправка за компарирование определяется по формуле
Dk = n Dl ,
где Dl – отличие длины ленты от 20 м и n – число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.
Поправка за температуру определяется по формуле
Dt = aD(t–t0)
где a – термический коэффициент расширения (для стали a = 0,0000125); t и t0 – температура ленты во время измерений и при компарировании. Поправку Dt учитывают, если ½t–t0½>10°.
Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D
d = D cosn , (8.2)
где n – угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где
Dn = d – D = D (cosn – 1) = -2D sin2 . (8.3)
По формуле (8.3) составляют таблицы, облегчающие вычисления.
Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.
Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.
Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.
Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами – глазным 1 и предметным 4.
|
|
|
Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона
Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 – 30¢.
Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.
Точность измерений лентой в разных условиях различна и зависит от многих причин – неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.
Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта di определяют по формуле
di = П – З,
где П и З – передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).
Если линия имеет наклон, необходимо учесть поправку
,
где h – превышение между концами пролёта, измеряемое нивелиром.
Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 – 1:10000.
Практическое
занятие № 1 Определение расстояний по картам с применением числового и
линейного масштабов
Цель
занятия
– научиться определять расстояний по картам с применением числового, линейного,
поперечного масштабов
Дидактическое
оснащение: карта
местности, линейка, калькулятор.
Задание:
рассчитать
длину линии на местности и длину отрезка на плане.
Краткие теоретические сведения
Масштаб – это отношение длины линии на карте, плане
(чертеже) Sp к длине горизонтального приложения соответствующей линии в
натуре (на местности) Sm.
Численный масштаб – 1/ М, правильная дробь, у которой
числитель равен 1, а знаменатель М показывает во сколько раз уменьшены линии
местности по сравнению с планом.
Например, масштаб 1:10000 означает, что все линии местности
уменьшены в 10000 раз, т.е. 1 см плана соответствует 10000 см на местности
или 1 см плана = 100 м на местности,
или 1 мм плана = 10 м на местности.
Следовательно, зная длину отрезка Sp плана по
формуле Sm=Sp*M можно вычислить длину линии на местности или по формуле Sp= Sm:M определить длину
отрезка на плане.
Например, длина линии на местности 252 м; масштаб плана
1:10000. Тогда длина линии на плане Sр=252м : 10000=0,0252м = 25,2мм.
И обратно, длина отрезка на плане равна 8,5 мм; масштаб
плана 1:5000. Требуется определить длину линии местности. Она будет 8,5 мм *
5000 = 42,5м.
Порядок
работы:
1.
Вычислите длину линии на местности Sm, длину
отрезка на плане Sp для данных, приведенных в таблице 1. Результаты запишите в
соответствующую графу таблицы.
2.
Замерить линейкой длину отрезка на плане Sp между городами, используя карту.
Определить длину линии на местности Sm для данных. Результаты запишите в
соответствующую графу таблицы.
Таблица
1
|
Масштаб |
Длина |
Длина |
Масштаб |
Длина |
Длина |
|
1:2000 |
80,4 |
1:10000 |
62,5 |
||
|
1:5000 |
380,5 |
1:25000 |
20,2 |
||
|
1:10000 |
536 |
1:5000 |
12,5 |
||
|
1:25000 |
625 |
1:50000 |
6,2 |
||
Содержание отчета: укажите номер практической работы, тему, цель, оборудование,
выполните задания методических указаний, сформулируйте и запишите вывод.
Контрольные вопросы
1. Виды масштабов, их практическое значение
для картографии.
2. Дайте понятие графические
масштабы.
Основой
решения задачи является масштаб карты
и линии координатной сетки. График
ориентирных углов, с выписанными на нем
сближением меридианов и склонением магнитной стрелки.
Схема
решения задачи следующая. По карте
измеряют линейкой (с применением
циркуля-измерителя) в мм длину линии и
по формуле численного масштаба вычисляют
в метрах на местности. На карте через
начальную точку заданного направления
проводят линию, параллельную вертикальной
линии координатной сетки (рис.3.3).
Транспортиром
измеряют острый угол от ближайшего
конца проведенной вертикальной линии
до заданного направления (дирекционный
румб направления линии). Составляют
график ориентирных углов, на котором
показывают заданное направление,
измеренный дирекционный румб, сближение
меридианов и склонение магнитной стрелки
(рис3.4) . По формулам связи вычисляют
дирекционный угол и истинный и магнитный
азимуты. Правильность вычислений
приближенно проверить графически по
графику ориентирных углов.
Рис.
3.3. Схема определения направления линииРис 3.4 График
ориентирных углов
Пример по данным рис.3.1
Результаты измерений: длина линии АВ
(горизонтальное проложение) на карте
130.0 мм, на местности d
= 1300 м. Дирекционный румб направления
АВ r=ЮЗ:130.
Дирекционный угол
= 1930.
Истинный азимут АИСТ
= 1900 38′.
Магнитный азимут АМ
=1840
26′.
-
Решение прямой и обратной геодезической задачи
Решение
прямой геодезической задачи.
Схема решения задачи следующая. Составить
расчетную схему по образцу рис.3.5.
Вычислить на микрокалькуляторе приращения
координат и по ним вычислить координаты
заданной точки.
Приращения координат можно вычислить
на микрокалькуляторе через дирекционные
румбы, определив знаки приращений по
названию румба. Можно вычислить приращения
координат через радианы, разделив
градусы на 57.29578. Например, угол в градусной
мере 34045, в
радианах будет равен (34+45/60)/57.29578=0.6065019.
Для контроля рекомендуется вычисления
вести дважды, по двум независимым
формулам.
Пример
По
измеренным по карте координатам точки
А, дирекционному углу и длине линии АВ
вычислены координаты точки В.
На
рис. 3.5 приведена расчетная схема, на
которую выписана исходная информация.
Дано:
ХА=6065675,
УА=
-188030 м, r=ЮЗ:130,
=1930,
d=1300 м. Определить: ХВ,
УВ.
х
отрицательное, у
– отрицательное.
Вычисление
приращений координат на микрокалькуляторе
по румбам через градусы. Программа
DEG:х=
d
Cos
r
= “13” “Cos”
“x”
“1300 “= 1267 м.; y=d
Sin
r
= ” 13″ “Sin”
“x”
“1300 = 292 м.
Координаты
точки В: X
B
= XA
± x
= 6065675 – 1267=6064408 м, УB
= УA
± у
= – 188030 – 292 = – 188322 м, (с учетом названия
румба).
Вычисление
координат точки В по дирекционным
углам через градусы:
XВ=XА+dСоs=”193”
“Cos” “x” “1300” “+” “6065675” =6064408 м.;
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
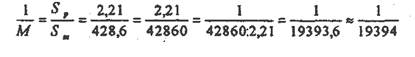






![inj_geo_1-245.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-245.jpg)
![inj_geo_1-247.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-247.jpg)
![inj_geo_1-248.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-248.jpg)



