Сфера, шар, сегмент и сектор. Формулы и свойства сферы
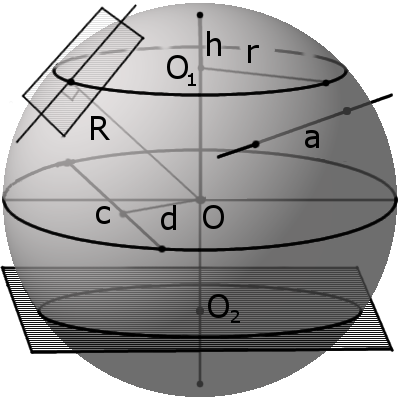
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
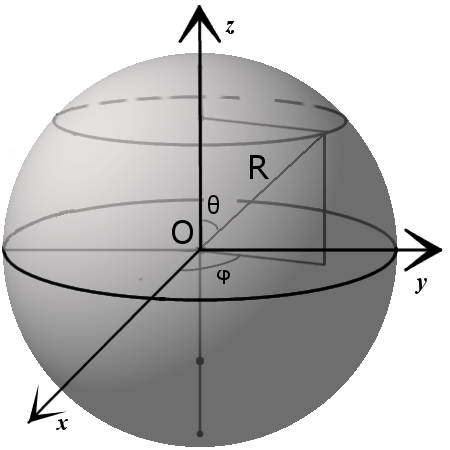
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
Основные свойства сферы и шара
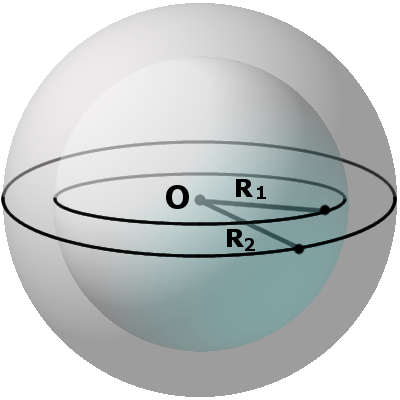
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
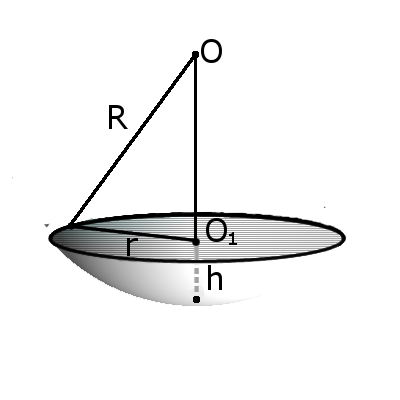
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R – h 2 )
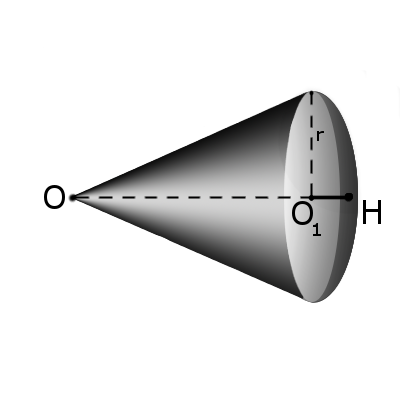
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Формула длины окружности через радиус или диаметр
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности – отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности – отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса
r – радиус окружности
D – диаметр окружности
Формула длины окружности через радиус или диаметр, (L):
Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-21-06-49-57
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
[/spoiler]
Ответ
Ответ:
L = 80π см.
Объяснение:
Сечение сферы – окружность, радиус которой найдем по Пифагору из треугольника, образованного перпендикуляром из центра сферы до плоскости (катет = 9 см), радиусом сферы (гипотенуза) и искомым радиусом сечения (второй катет).
Rc = √(41² – 9²) = 40 см.
Длина линии сечения – длина окружности – равна 2*π*R или
L = 2π*40 = 80π см.

Ответы и объяснения
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 68595 Сфера, радиусом 15см, пересечена…
Условие
![]()
63cf77d914bf592bc0291e7e
24.01.2023 09:18:41
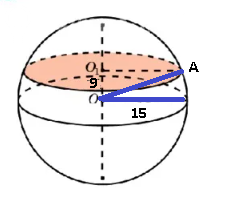
Сфера, радиусом 15см, пересечена плоскостью, проходящей на расстоянии 9см от центра сферы. Найти длину линии пересечения сферы и плоскости.
математика
1841
Решение
![]()
5f3ea7e3faf909182968ddd9
24.01.2023 10:15:17
★
R_(сферы)=15
ОО_(1)=9
r_(сечения)=O_(1)A
O_(1)A^2=OA^2-O_(1)O^2=15^2-9^2=(15-9)(15+9)=6*24
O_(1)A=12
r=12
C=2π*r=2π*12=[b]24π[/b]
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Учеба и наука
Вопрос задан анонимно
ноябрь 7, 2014 г.
-
Всего ответов: 1
-
 плоскость пересекает сферу по окружности диаметром 2 корня из 2 m, длина окружности =pi *2 *корень из 2 m
плоскость пересекает сферу по окружности диаметром 2 корня из 2 m, длина окружности =pi *2 *корень из 2 mЛучший ответ по мнению автора
Похожие вопросы
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
![]()
3
Найдите длину линии сечения
1 ответ:
![]()
0
0
Ответ:
L = 80π см.
Объяснение:
Сечение сферы – окружность, радиус которой найдем по Пифагору из треугольника, образованного перпендикуляром из центра сферы до плоскости (катет = 9 см), радиусом сферы (гипотенуза) и искомым радиусом сечения (второй катет).
Rc = √(41² – 9²) = 40 см.
Длина линии сечения – длина окружности – равна 2*π*R или
L = 2π*40 = 80π см.
Читайте также
![]()
И.к. АМ=МС => треугольник АВС равнобедренный
Угол С = 180-(70/2+90) = 180-125 = 55 градусов
Угол А= угол С = 55 градусов
![]()
Надо использовать свойство:
В параллельных плоскостях линии сечения параллельны.
Для примера приведен один из вариантов.
Остальные есть попроще, в других находить линии пересечения по аналогии с приведенным примером.
![]()
Надо было см перевести в мм и все ьы пооучилось
![]()
R=a^2/корень квадратный из(2*а)^2=25/корень квадратный из(2*5)^2-6^2=25/корень квадратный из 10^2-6^2=25/корень квадратный из(10-6)(10+6)=25/корень квадратный из100+60-60-36=25/8=3,125 как то так,если что то не понятно обращайся.
![]()
<span>В результате вращения треугольника образуется 2 конуса с общим основанием, растояние между вершинами у которого будет равно 4√3. Угол при основании (не у вершин) равен 120 градусов. Так как треугольник равнобедренный то можно найти радиус. В прямоугольном треугольнике(надеюсь вы его найдете) углы будут равны 90,60,30,а сторона напротив угла 30 градусов равна половине гипотинузы, т.е. √3-это радиус основания конусов. Длина окружности равна 2* π *r (r-радиус).Длина окружности равна 2√3* π . Площадь поверхности равна ФИГУРЫ равна 2* π *√3*2* π *√3=12* π ^2.(На 2 умножаем потому что конуса 2). Ответ: 12π^2/</span>
