Как найти длину ломаной формула

Ломаная линия

• Замкнутая и незамкнутая ломаная
• Самопересекающаяся ломаная
• Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки  AB,  BC,  CD  и  DE  — это звенья ломаной. Точки  A,  B,  C,  D  и  E  — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная  ABCDE  или ломаная  EDCBA.

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная  ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная  ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки  F,  T,  K  — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник  ABCDE.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Математика, 2 класс. Урок №13.

Длина ломаной. Закрепление

Перечень вопросов, рассматриваемых в теме:

– Как найти длину ломаной?

Глоссарий по теме:

Ломаная – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.

Звенья – отрезки, из которых состоит ломаная.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина ломаной – это сумма длин всех её звеньев.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35

2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 – с.20, 21

3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 – с.20, 21, 25

Теоретический материал для самостоятельного изучения

На рисунке мы видим ломаную линию, состоящую из трёх звеньев.

Как найти длину ломаной линии? Это можно сделать двумя способами.

Первый способ. Сначала узнаем длину каждого звена с помощью линейки

Длина первого звена 4 см.

Длина второго звена 6 см.

Длина третьего звена 5 см.

Найдем сумму этих длин.

4+6+5=15 (см)

Найдем длину ломаной вторым способом.

Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.

Накладываем циркуль на второй отрезок, переносим его на прямую.

Накладываем циркуль на третий отрезок, переносим его на прямую.

Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.

Выводы: длину ломаной можно находить двумя способами.

Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.

Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.

Тренировочные задания.

1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см

Варианты ответов:

10 см 8 см 7 см

Правильный вариант:

10 см 8 см 7 см

2. Расположите ломаные линии по порядку: от самой короткой до самой длинной

Правильный вариант: Найдем длину каждой ломаной

6 + 2 + 2 = 10 см

7 + 5 = 12 см

2 + 1 + 3 +2 = 8 см

3 + 1 + 5 = 9 см

Расставим в порядке возрастания:

2 + 1 + 3 + 2 = 8 см

3 + 1 + 5 = 9 см

6 + 2 + 2 = 10 см

7 + 5 = 12 см

Вчера (или позавчера) поступило предложение разобрать задание для «поступления в школу “СУНЦ МГУ”, которая попадается под 4-ым номером»:

Есть две параллельные прямые, расстояние между ними пусть будет L. Даны точки A и B на первой и второй прямой соответственно, пусть расстояние между их проекциями на одну из прямых равно a. Найти минимальную длину ломаной APQB, где P лежит на второй прямой, а Q – на первой.

Оказалось, не просто, поэтому мнение экспертов в комментариях как никогда «важнО и нужнО». Это #геометрия, а значит — очень интересно! Пробуем?

Расстояние

Начнём с простого, но, как оказалось, не очевидного. Понятия расстояния. Под одним из решений в комментариях (теперь уже удален), читательница высказала мнение, что расстояние – не обязательно кратчайший путь, только когда это оговаривается условием. Так вот…

Три вида расстояний:

1. Расстояние между точками A и B – отрезок AB;
2. Расстояние между точкой A и прямой BC – перпендикуляр, проведенный из точки A к прямой BC;
3. Расстояние между параллельными прямыми AB и CD – перпендикуляр, проведённый из любой точки принадлежащей прямой AB к прямой CD.

Эти три расстояния никогда не оговариваются условием, как «кратчайшие».

Расстояние между точками

Проверьте, насколько Вам понятно понятие расстояния между точками, найдите расстояние между точками A и B на рисунке ниже, проверьте свои ответы пролистав галерею:

Вывод

Неважно, как две точки располагаются на плоскости – расстояние между ними, это всегда отрезок, началом и концом которого будут данные точки (хоть на двух прямых эти точки, хотя на одной, хоть на отрезках).

Расстояние между тремя точками. Ломаная

Усложним, добавим ещё одну точку. Точку C. Как найти расстояние между тремя точками? А как найти кратчайшее расстояние между тремя точками?

Тут всё зависит от взаимного расположения. Сразу оговоримся, что точки совпадать не могут. Тогда:

1. Три точки располагаются на одной прямой;
2. Три точки НЕ располагаются на одной прямой.

В первом случае: это отрезок началом и концом которого будут две точки, а третья принадлежит данному отрезку.

Во втором случае: взаимное расположение точек таково, что можно построить треугольник ∆ABC, а дальше всё зависит от условия. Но, так или иначе, это будет связано со сторонами треугольника ∆ABC и ломаной, которая будет образована двумя сторонами этого треугольника.

А что, если кратчайшее расстояние между тремя (не лежащими на одной прямой) точками нужно найти самостоятельно? Например, даны т. A и C – на первой параллельной прямой, а т. B – на второй. Точки A и C перемещать нельзя. Найти такое положение т. B, чтобы длина ломаной ABC была наименьшей.

Уверен, у Вас получилось найти такую ломаную… Но что, если Вы ошиблись? Как это проверить? А если не ошиблись и догадались верно, как доказать? Нарисуйте свой вариант и проделайте всё следующее.

Я ошибусь нарочно, построю ломаную ABC, как показано на рисунке:

Длина ломаной ABC – наименьшая? Проверим это, достроим т. D, симметричную т. C относительно второй прямой (содержащей т. B). И соединим т. B и D. Треугольник ∆CBD – равнобедренный (BE – срединный перпендикуляр).

Тогда, по свойству длины отрезков, очевидно:

AB + BC = AB + BD – этим выводом ниже еще воспользуемся.

Соединим т. A и D. Точку пересечения отрезка AD со второй прямой назовём т. K.

У меня получился ∆ABD, а у Вас? Если да, то Вы тоже ошиблись с выбором B. А если т. K и B совпали (треугольник не получился), то это и есть самый короткий путь от т. A к C, через т. B. В моём случае ломаная AKC будет иметь меньшую длину, чем ломаная ABC.

Почему? Благодаря теореме, которая называется неравенство треугольника:

Любая сторона в треугольнике всегда меньше суммы длин двух других.

А значит:

AD < AB + BD — неравенство треугольника ∆ABD;
AB + BD = AB + BC — доказывали выше;
AD = AK + KC — медиан CK в прямоугольном ∆ADC;

AK + KC < AB + BC — длина ломаной AKC меньше.

Конечно, возможны и другие способы это доказать.

Способ №1

Теорема Пифагора, но тут придётся проверять несколько вариантов, обобщать, как-то обосновать ответ.

Способ №2

Производные, но это ещё 9 класс. Так что в другой раз.

Способ №3 или «А при чём тут эллипс?»

Эллипс. Опять не по программе 9-го класса, но очень интересно.

Способ №4

Ваш способ, предложите его в комментариях. Нужно Ваше экспертное мнение.

Заключение

Наименьшая длина ломаной ABC (из трёх точек, не лежащих на одной прямой и не совпадающих) достигается, когда AB = BC.

Зигзаг. Ответ

На поставленный в самом начале вопрос.

Какой будет эта ломаная? И какой будет наименьшая длина ломаной?

Это будет зигзаг, т.е. какое-то количество равных прямоугольников с одной диагональю симметричных друг другу относительно оси (высоты). При этом количество точек (а значит и равных симметричных прямоугольников) на параллельных прямых не имеет значения.

На рисунке ниже буквой A обозначим данные точки, а буквой B – их проекции на другую прямую. Нечётные порядковые номера точек (A₁, A₃, A₅ и т.д.) на первой параллельной прямой, а чётные – на второй. A₁B₁A₂B₂ – прямоугольник с диагональю A₁A₂.

Если это прямоугольники, а ломаная – сумма одинаковых диагоналей прямоугольников, можно вывести формулу для нахождения наименьшей длины такой ломаной:

Ответ: 3 √(L² + a²/9)

Спасибо, что дочитали до конца. Надеюсь, что Вам понравилось. Ставьте лайк, оформляйте подписку, ну вот это вот всё 😂

Читайте также:

🔴Пропорциональные отрезки и площадь четырёхугольника

🔴Пропорциональные отрезки в треугольнике / Геометрия / ОГЭ

🔴Пропорциональные отрезки (и не только) в треугольнике. Часть 2

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA .

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Ломаная

Определение 1. Ломаной (ломаной линией) ( small A_1A_2. A_A_n ) называется геометрическая фигура, которая состоит из ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки( small [ A_A_ ]) и ( small [ A_A_ ]) при ( small k=1,2. n-2 ) не лежат на одной прямой.

Можно дать и другое определение ломаной:

Определение 2 . Если ( small A_1, A_2, . A_n ) различные точки, никакие проследовательные три из которых не лежат на одной прямой, то совокупность отрезков ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) называется ломаной или ломаной линией.

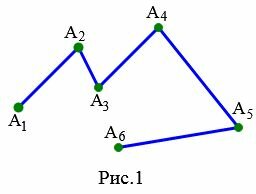
На рисунке 1 изображена ломаная состоящая из пяти отрезков ( small [ A_1A_2 ]) , ( small [ A_2A_3 ]), ( small [ A_3A_4 ]), ( small [ A_4A_5 ]), ( small [ A_5A_6 ]), которые последовательно соединены своими концами.

Невырожденная ломаная

Ломаная, описанная в определении 1 называется невырожденной ломаной.

На рисунке 1 ломаная ( small A_1A_2A_3A_4A_5A_6 ) является невырожденной поскольку отрезки ( small [ A_1A_2 ]) и ( small [ A_2A_3 ]), ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]), ( small [ A_3A_4 ]) и ( small [ A_4A_5 ]), ( small [ A_4A_5 ]) и ( small [ A_5A_6 ]) не лежат на одной прямой.

Вырожденная ломаная

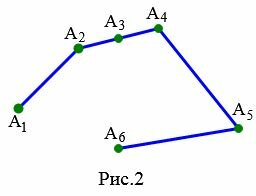
Определение 3 . Если ( small A_1, A_2, . A_n ) различные точки, и среди них существуют проследовательные три точки, лежащие на одной прямой, то совокупность отрезков ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) называется вырожденной ломаной или вырожденной ломаной линией.

На рисунке 2 изображена ломаная ( small A_1A_2A_3A_4A_5A_6 ). Эта ломаная является вырожденной поскольку отрезки ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]) лежат на одной прямой.

Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.

Звенья ломаной

Звеньями называют отрезки, из которых состоит ломаная.

Ломаная ( small A_1A_2A_3A_4A_5A_6 ), изображенная на рисунке 1 состоит из звеньев ( small [ A_1A_2 ]) , ( small [ A_2A_3 ]), ( small [ A_3A_4 ]), ( small [ A_4A_5 ]), ( small [ A_5A_6 ]).

Вершины ломаной

Конечные точки звеньев ломаной называются вершинами.

На рисунке 1 изображена ломаная ( small A_1A_2A_3A_4A_5A_6 ), состоящая из шести вершин: ( small A_1, A_2, A_3, A_4, A_5, A_6 ).

Смежные звенья ломаной

Смежные звенья ломаной − это звенья имеющие общую вершину.

На рисунке 3 смежными звеньями ломаной ( small A_1A_2A_3A_4A_5A_6 ) являются звенья: ( small [ A_1A_2 ]) и ( small [ A_2A_3 ]), ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]), ( small [ A_3A_4 ]) и ( small [ A_4A_5 ]), ( small [ A_4A_5 ]) и ( small [ A_5A_6 ]).

Смежные вершины ломаной

Смежными вершинами ломаной называют вершины одного звена ломаной.

На рисунке 3 смежными вершинами ломаной ( small A_1A_2A_3A_4A_5A_6 ) являются вершины: ( small A_1) и ( small A_2), ( small A_2) и ( small A_3), ( small A_3) и ( small A_4 ), ( small A_4) и ( small A_5), ( small A_5) и ( small A_6).

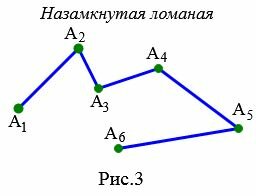
Незамкнутая ломанная

Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).

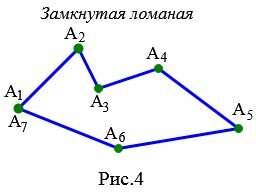
Замкнутая ломанная

Определение 4 . Замкнутым является ломаная ( small A_1A_2. A_A_n ), первая ( small A_1) и последняя ( small A_n ) точки которой совпадают друг с другом и отрезки ( small A_1A_2 ) и ( small A_A_n ) не лежат на одной прямой.

На рисунке 4 ломаная ( small A_1A_2A_3A_4A_5A_6A_7 ) является замкнутым, так как точки: ( small A_1) и ( small A_7) совпадают и отрезки ( small A_1A_2) и ( small A_6A_7) не лежат на одной прямой.

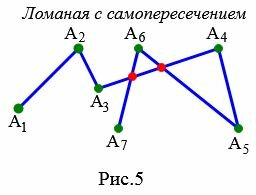
Ломаная с самопересечением

Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.

Ни рисунке 5 ломаная ( small A_1A_2A_3A_4A_5A_6A_7 ) имеет самопересечение, так как звенья ( small A_5A_6 ) и ( small A_6A_7 ) имеют общие точки со звеном ( small A_3A_4 ).

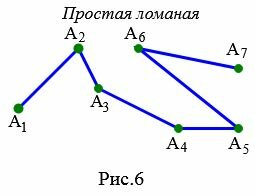
Простая ломаная

Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.

Длина ломаной

Длина ломаной равна сумме длин всех звеньев ломаной: ( small d= A_1A_2+A_2A_3+. +A_A_n, ) где ( small n ) − количество вершин ломаной.

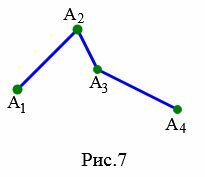
Теорема. Длина ломаной больше расстояния между первым и последним точками.

Доказательство. Для доказательства теоремы рассмотрим ломаную ( small A_1A_2A_3A_4 ) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины ( small A_1, A_2, A_3 ) не лежат на одной прямой. Тогда имеет место неравенство треугольников:

( small A_1A_2+A_2A_3 > A_1A_3 ).

(1)

Для точек ( small A_1, A_3, A_4 ) имеет место следующее нестрогое неравенство:

( small A_1A_3+A_3A_4 ≥ A_1A_4 ).

(2)

В выражении (2) мы не применяли строгое неравенство поскольку вершины ( small A_1, A_3, A_4 ) ломаной не являются соседними вершинами и могут лежать на одной прямой.

В неравенстве (2) вместо слагаемого ( small A_1 A_3) подставим сумму ( small A_1A_2+A_2A_3 ) из (1), которая больше, чем ( small A_1 A_3). Тогда получим:

( small A_1A_2+A_2A_3+A_3A_4 > A_1A_4 ).

Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.

Аналогично доказывается теорема для ломанной с любым количеством звеньев.

Ломаная

Концы ломаной — ее первая и последняя вершины A₁ и A₂.

Простая ломаная и с пересечением

Правило
Рис. 1

Рис. 2

Простая ломаная — ломаная без самопересечений.

Рис. 1 — простая ломаная.
Рис. 2 — ломаная с самопересечением в точке B.

Длина ломаной — сумма длин ее звеньев.

Теорема:

Замкнутая ломаная

Замкнутая ломаная — ломаная, концы которой совпадают.