18. Ломаная
Это надо знать
Ломаная – это геометрическая фигура, которая состоит из нескольких отрезков не лежащих на одной прямой, соединенных последовательно своими концами.
Отрезки называют звеньями ломаной, а точки — вершинами ломаной.
На рисунке ломаная ABCD. У этой ломаной 4 вершины: A, B, C, D и три звена: AB, BC, CD.
Если начальная и конечная точка ломаной совпадают, то такую ломаную называют замкнутой.
Ломаные ABCDE, NMLK – незамкнутые.
Ломаные FHG, ZVTP – замкнутые.
Длину ломаной определяет как сумму длин звеньев ломаной.
Найдем длину ломаной ABCDEF:
ABCDEF=AB+BC+CD+DE+EF=2+4+3+1+5=15 (см)
Домашнее задание
(на 25.09)
п. 2.7
№ 2.87, 2.88
Дополнительная задача
Муравей ползет по ребрам куба по выделенному маршруту из точки А в точку Р, поворачивая лишь в вершинах. Длина стороны куба равна 20 см.
1) сколько сантиметров прополз муравей?
2) найдите длину самого короткого маршрута из точки А в точку Р.

Математика, 2 класс. Урок №13.
Длина ломаной. Закрепление
Перечень вопросов, рассматриваемых в теме:
– Как найти длину ломаной?
Глоссарий по теме:
Ломаная – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.
Звенья – отрезки, из которых состоит ломаная.
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
Длина ломаной – это сумма длин всех её звеньев.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35
2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 – с.20, 21
3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 – с.20, 21, 25
Теоретический материал для самостоятельного изучения
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.

Как найти длину ломаной линии? Это можно сделать двумя способами.
Первый способ. Сначала узнаем длину каждого звена с помощью линейки

Длина первого звена 4 см.

Длина второго звена 6 см.

Длина третьего звена 5 см.
Найдем сумму этих длин.
4+6+5=15 (см)
Найдем длину ломаной вторым способом.
Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.


Накладываем циркуль на второй отрезок, переносим его на прямую.


Накладываем циркуль на третий отрезок, переносим его на прямую.

Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.

Выводы: длину ломаной можно находить двумя способами.
Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.
Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.


Тренировочные задания.
1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см
Варианты ответов:
10 см 8 см 7 см
Правильный вариант:
10 см 8 см 7 см
2. Расположите ломаные линии по порядку: от самой короткой до самой длинной




Правильный вариант: Найдем длину каждой ломаной
6 + 2 + 2 = 10 см
7 + 5 = 12 см
2 + 1 + 3 +2 = 8 см
3 + 1 + 5 = 9 см
Расставим в порядке возрастания:

2 + 1 + 3 + 2 = 8 см

3 + 1 + 5 = 9 см

6 + 2 + 2 = 10 см

7 + 5 = 12 см
Ломаная линия
- Замкнутая и незамкнутая ломаная
- Самопересекающаяся ломаная
- Длина ломаной
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE
или ломаная EDCBA
.
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCDE.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ответ: 17 см.
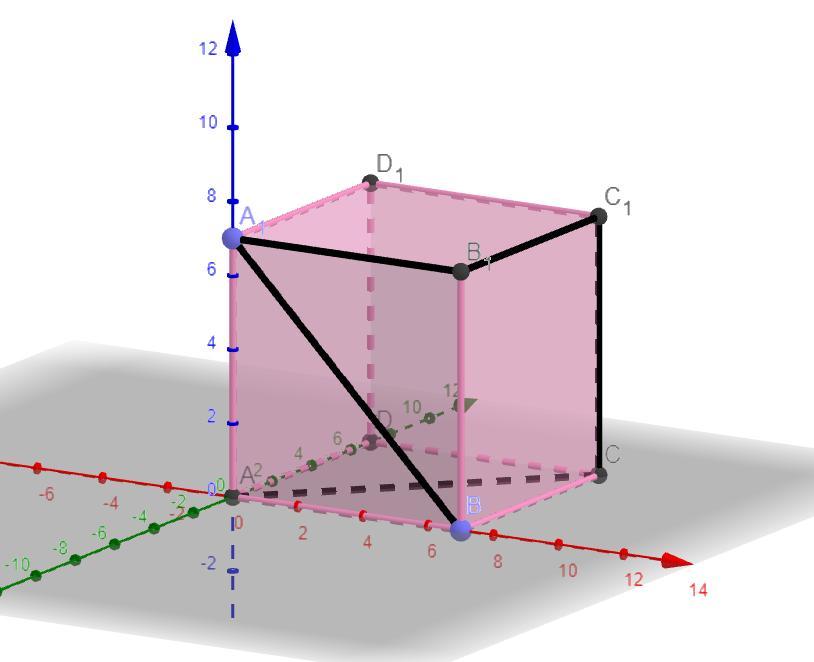
Ответ:
Объяснение: После построения куба видим, что ломаная состоит из 3 сторон квадрата и двух диагоналей квадрата.
Диагонали находим по теореме Пифагора:
Длина ломаной равна
Приложения:
Геометрия обладает особой выразительностью:
можно, посмотрев на иллюстрации, уловить
математический смысл текста.
Предмет геометрии составляют идеальные образы
– геометрические фигуры. В архитектуре же эти
идеальные образы получают материальное
воплощение, а вместе с ним и новое звучание.
С точки зрения математики в архитектурных
сооружениях всех времён царит единство числа и
фигуры. Но истинный зодчий так соединяет
геометрию “математическую” и геометрию
“архитектурную”, что никогда не удаётся до
конца раскрыть тайны очарования его творений.
Знаменитый зодчий ХХ века, француз Ле Корбюзье
писал: “Архитектура – это способность нашего
сознания закреплять в материальных формах
чувство эпохи”.
Что означают эти слова?
Какова она – эта красота?
И каково оно – “чувство эпохи”?
Как они связаны с геометрией?
И дворцы Востока, и древнерусские храмы, и
готические соборы – это часть каменной летописи
мира. Но для нас это не просто страницы истории –
это ещё и зримая геометрия Добра, Красоты,
Совершенства. И геометрия несёт свою долю
ответственности за наше совершенство, на каком
бы уровне строгости мы её не изучали.
Мы с вами продолжаем идти маленькими шагами к
Храму, который зовётся Геометрией.
ХОД УРОКА.
Рисунок 1.
Сравните первую и вторую геометрические
фигуры. Что общего между ними вы заметили?
Рисунок 2.
Отметьте все фигуры, которые устроены так же,
как фигуры на первом рисунке.
Разбейте их на группы.
Почему вы так распределили эти фигуры?
Как бы вы их назвали?
Итак, такие геометрические фигуры называются
ломаными линиями или просто – ломаными.
Какие ломаные вошли в первую группу? А во
вторую? А теперь изобразите отдельно все
оставшиеся ломаные. Почему они не вошли в группы?
Все ломаные состоят из отрезков, которые
называются звеньями ломаной.
Рисунок 3.
Это простые незамкнутые ломаные.
Рисунок 4.
Это простые замкнутые ломаные.
Рисунок 5.
Эти ломаные не являются простыми.
Крайние точки называются концами ломаной или
началом и концом ломаной.
Посмотрим ещё раз внимательно на
геометрические фигуры, изображённые на рис.4.
Можете ли вы выделить уже знакомые
геометрические фигуры?
Ученик: Ромб, квадрат, шестиугольник,
параллелограмм.
Учитель: “Посмотрите на них с точки зрения
ломаной”.
Ученик: “Это простые замкнутые ломаные”
Учитель: “Как ещё можно назвать эти
фигуры?”
Ученик: “Многоугольники”.
Учитель: “О каком понятии шла речь на
уроке?”
Ученик: “О ломаной”.
Учитель: “Сформулируем тему сегодняшнего
урока и его цель”.
На доске записывается тема урока, ребята пишут
в тетрадях.
А сейчас наступает момент, когда наша работа с
фигурами может стать особенно красивой. И
красота эта возникнет благодаря неожиданным,
оригинальным соединениям различных ломаных на
чертеже.
Рисунок 6.
Присмотритесь внимательно к работам мастеров.
Поучимся у них умению соединять геометрические
фигуры так, чтобы получилась бы настоящая
картина из фигур.
Чтобы легче было понять схемы, посмотрим на
каждый шаг построения.
Рисунок 7.
Разобравшись в схеме, выполните построение у
себя в тетрадях.
А теперь посмотрим на ломаную с другой стороны.
Изобразим куб у себя в тетрадях. (На доске –
изображение куба.)
Рисунок 8.
Можно ли из точки А попасть в точку А1,
двигаясь по рёбрам куба и побывав при этом во
всех вершинах куба ровно один раз? Покажите путь
и назовите получившуюся ломаную.
Ответ: АDD1C1BB1A1
А теперь решим такую задачу.
Задача 1.
Мы имеем стеклянный куб. На его поверхности
расположена ломаная с вершинами, совпадающими с
некоторыми вершинами куба.
Изобразите, как выглядит данная ломаная
спереди, сверху и слева.
Рисунок 9.
Как проходят звенья ломаной?
Ученик: “Звенья ломаной проходят по рёбрам
куба”.
Задача 2.
В этой задаче звенья ломаной идут не только по
рёбрам куба, но и по диагонали грани куба, а
вершины, как и прежде, находятся в некоторых
вершинах куба.
Изобразите вид спереди, вид сверху и вид слева
этой ломаной.
Рисунок 10.
При работе с конструкциями из кубиков
определять виды конструкции было легче, так как
соседние кубики имели общую грань. Здесь задача
посложнее. Чтобы представить себе виды ломаной,
приходится мысленно отпечатывать ломаную на
одну, другую, третью грани куба.
Итак, в центре всех наших размышлений,
разговоров и действий всегда находится
геометрическая фигура, какой бы она не была:
плоской или пространственной.
Итог урока.
- О чём шла речь на уроке?
- В каких задачах мы используем ломаную?
Домашнее задание.
Попытайтесь своим оригинальным способом
соединить ломаные и получить орнамент.
