Как найти длину маятника формула физика

Как найти длину маятника формула физика

Расчет длины маятника

Маятник — это тело или система тел, подвешенная в поле тяжести и совершающая механические колебания.

Формула расчета длины маятника:

L = (T / 2π) 2 * g, где

L — длина маятника в метрах;
T — период колебаний в секундах;
g — ускорение свободного падения в м/с 2 .

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета длины маятника по простой математической формуле в зависимости от периода колебаний и ускорения свободного падения. С помощью этой программы вы в один клик сможете рассчитать длину маятника.

Расчет длины нити математического маятника

Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле , где — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет секунды.

Решение задачи

В данном уроке показано, как грамотно рассчитать длину нити математического маятника. По условию задана формула , с помощью которой приблизительно вычисляются колебания маятника. — это период колебания маятника, который известен по условию задачи ( секунды), а – это длина нити маятника, которую и необходимо рассчитать. Для решения задачи достаточно преобразовать формулу (представленную в виде алгебраического выражение) и подставить в нее известные данные. Для этого из формулы выражается переменная , в процессе этого выполняются операции упрощения выражения. Далее, для получения окончательного ответа, вместо переменной подставляется его числовое значение. Ответ представлен в виде десятичной дроби

При подготовке к ОГЭ можно успешно воспользоваться решением этой задачи, в частности при решении задач типа ОГЭ 20.

Как найти длину нити

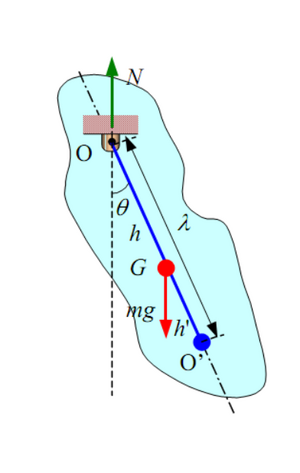
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол появляется касательная составляющая силы тяжести (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Если обозначить через линейное смещение маятника от положения равновесия по дуге окружности радиуса , то его угловое смещение будет равно . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению , а

Только в случае малых колебаний , когда приближенно можно заменить на математический маятник является гармоническим осциллятором , т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка ; при этом величина отличается от не более чем на . Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение маятника пропорционально его смещению , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника .

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс физического маятника находится ниже оси вращения на вертикали, проходящей через ось. При отклонении маятника на угол возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь – расстояние между осью вращения и центром масс .

Здесь – собственная частота малых колебаний физического маятника .

Более строгий вывод формул для и можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение есть вторая производная углового смещения по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции можно выразить через момент инерции относительно оси, проходящей через центр масс маятника и параллельной оси вращения:

Окончательно для круговой частоты свободных колебаний физического маятника получается выражение:

Источник

Физика 9 класс

Анонимный вопрос

1 июня 2018  · 8,0 K

ОтветитьУточнить

Ирина С.6,1 K

Книги, звери и еда – это хобби навсегда.  · 19 янв 2019

Формула для расчета периода математического маятника:

T=2*π*sqrt(l/g), где l-длина математического маятника, g-ускорение свободного падения. Из нее можно получить формулу для l:

l=(T^2*g)/(4*π^2)=(4^2*10)/(4*3.14^2)=4.06 м.

7,9 K

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Источник

Физическим
маятником
называется твердое тело, закрепленное
на неподвижной горизонтальной ocи (оси
подвеса), не проходящей через центр
тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести.

Вывод
периода:

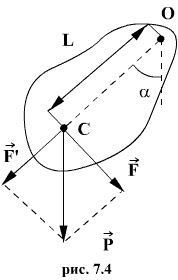
При небольших углах отклонения α (рис.
7.4) физический маятник так же совершает
гармонические колебания. Будем считать,
что вес физического маятника приложен
к его центру тяжести в точке С. Силой,
которая возвращает маятник в положение
равновесия, в данном случае будет
составляющая силы тяжести – сила F.

Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла α. С учетом малости угла α

.
Используем основное уравнение динамики
вращательного движения


 .
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид


.
Решение
этого уравнения

Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического маятника,
т.е. 
 или


.
Из этого соотношения определяем

.
Данная формула определяет приведенную
длину физического маятника, т.е. длину
такого математического маятника, период
колебаний которого равен периоду
колебаний данного физического маятника.

21.23.
Выведите уравнение колебательного
движения, являющегося суперпозицией
гармонических колебаний одного
направления с близкими частотами.
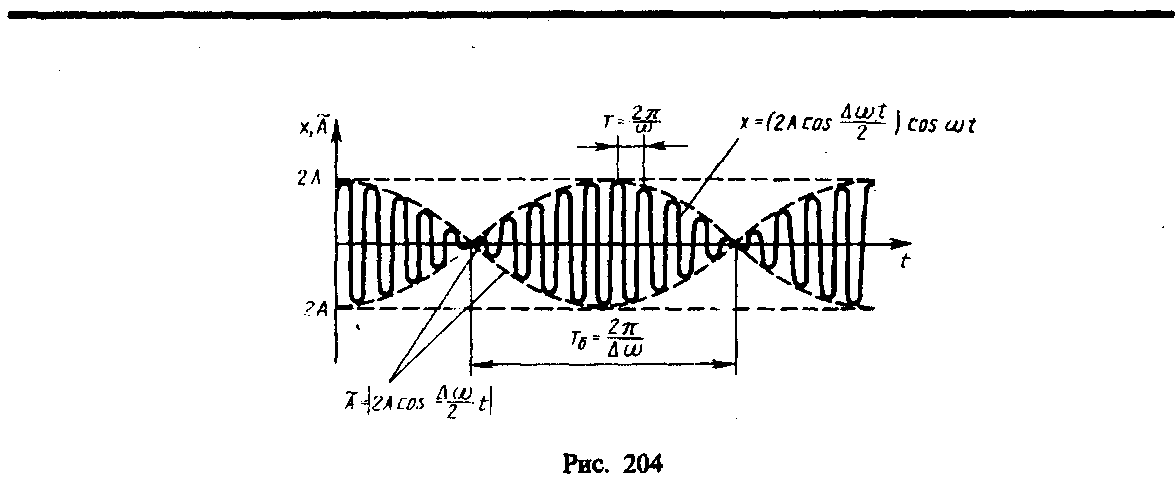
Изобразите результирующее колебание
на графике. Как называется такой вид
колебания?

Для
практики особый интерес представляет
случай, когда два складываемых
гар­монических колебания одинакового
направления мало отличаются по частоте.
В ре­зультате сложения этих колебаний
получаются колебания с периодически
изменяющей­ся амплитудой. Периодические
изменения амплитуды колебания, возникающие
при сложении двух гармонических колебаний
с близкими частотами, называются
биениями. Пусть амплитуды складываемых
колебаний равны А, а частоты равны 
и +,
причем <<.
Начало отсчета выберем так, чтобы
начальные фазы обоих колебаний были
равны нулю:

Складывая эти выражения и учитывая, что
во втором сомножителе /2<<,
найдем

(144.3).
Результирующее колебание (144.3) можно
рассматривать как гармоническое с
частотой ,
амплитуда Аб,
которого изменяется по следующему
периодическому закону:

(144.4).
Частота изменения Аб
в два раза больше частоты изменения
косинуса (так как берется по модулю),т.
Е. частота биений равна разности частот
складываемых колебаний:

Период биений

22.Сложение
взаимно-перпендикулярных гармонических
колебаний. Получите уравнение траектории
частицы, колеблющейся по осям х и у с
одинаковой частотой. Каковы траектории
при колебаниях по взаимно перпендикулярным
осям с кратными частотами?

Рассмотрим
результат сложения двух гармонических
колебаний одинаковой час­тоты ,
происходящих во взаимно перпендикулярных
направлениях вдоль осей х и у. Для
простоты начало отсчета выберем так,
чтобы начальная фаза первого колебания
была равна нулю, и запишем


(145.1),
где 
— разность фаз обоих колебаний, А и В —
амплитуды складываемых колебаний.
Уравнение траектории результирующего
колебания находится исключением из
выражений (145.1) параметра t.
Записывая складываемые колебания в
виде

и заменяя во втором уравнении cost
на х/А и sint
на

,
получим после несложных преобразований
уравнение эллипса, оси которого
ориентированы относите­льно координатных
осей произвольно:

(145.2)

Так
как траектория результирующего колебания
имеет форму эллипса, то такие колебания
называются эллиптически поляризованными.

25.
Какие силы называют квазиупругими?
Каков характер движения тела под
действием этих сил? Запишите дифференциальное
уравнение гармонических незатухающих
колебаний и его решение. Выведите формулу
для расчета периода.

КВАЗИУПРУГАЯ
СИЛА –
направленная к центру О сила. модуль
к-рой пропорционален расстоянию r от
центра О до точки приложения силы
(F=-cr),
где с –
постоянный коэф., численно равный силе,
действующей на единице расстояния. К.
с. является силой центральной и
потенциальной с силовой ф-цией U=-0,5cr2.
Примерами К. с. служат силы упругости,
возникающие при малых деформациях
упругих тел (отсюда и сам термин “К.
с.”). Приближённо К. с. можно также
считать касательную составляющую силы
тяжести, действующей на матем. маятник
при малых его отклонениях от вертикали.
Для материальной точки, находящейся
под действием К. с., центр О является
положением её устойчивого равновесия.
Выведенная из этого положения точка
будет в зависимости от нач. условий или
совершать около О прямолинейные гармонич.
колебания, или описывать эллипс (в
частности, окружность).

Линейное
неоднородное дифференциальное уравнение:


(147.5)
Применяем
впоследствии его решение для вынужденных
колебаний конкретной физической природы
(x0 в
случае механических колебаний
равно F0/m, в
случае электромагнитных — Um/L).

Решение
уравнения равно сумме общего решения


(146.5)
однородного урав­нения

и
частного решения неоднородного уравнения.
Частное решение найдем в комплексной
форме. Заменим правую часть уравнения
(147.5) на комплексную величину х0
:

(147.6). Частное
решение этого уравнения будем искать
в виде

Подставляя
выражение для s и
его производных 
 в
уравнение (147.6), получаем


 
(147.7). Так как это
равенство должно быть справедливым для
всех моментов времени, то время t из
него должно исключаться. Отсюда следует,
что h=w. Учитывая
это, из уравнения (147.7) найдем величину s0 и
умножим ее числитель и знаменатель на 


.
Это комплексное число удобно представить
в экспоненциальной форме:

,
где

(147.8);

(147.9)

Следовательно,
решение уравнения (147.6) в комплексной
форме примет вид

Его
вещественная часть, являющаяся решением
уравнения (147.5), равна

(147.10)

где А и j  задаются
соответственно формулами (147.8) и (147.9).

Таким
образом, частное решение неоднородного
уравнения (147.5) имеет вид

(147.11). Решение
уравнения (147.5) равно сумме общего решения
однородного уравнения

 
(147.12). (см. (146.5)) и частного решения
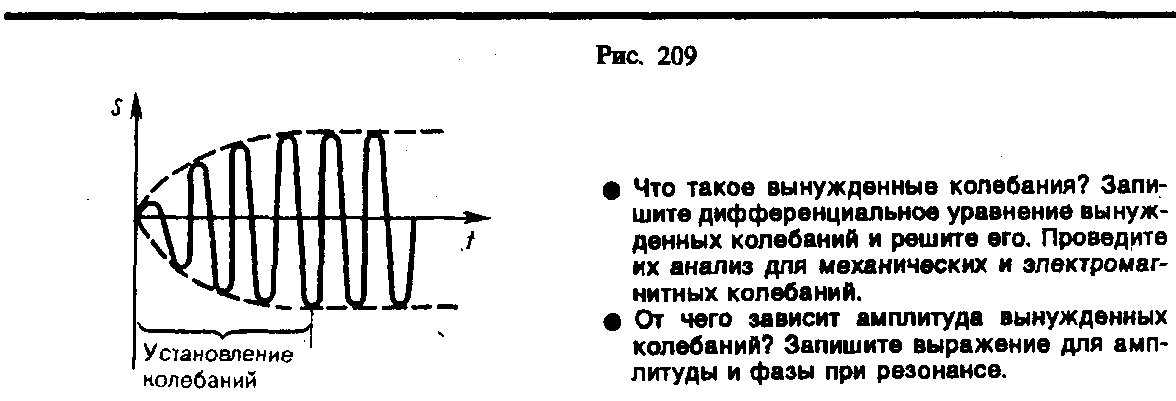
(147.11). Слагаемое (147.12) играет существенную
роль только в начальной стадии процесса
(при установлении колебаний) до тех пор,
пока амплитуда вынужденных колебаний
не достигнет значения, определяемого
равенством (147.8). Графически вынужденные
колебания представлены на рис. 209.
Следовательно, в установившемся режиме
вынужденные колебания происходят с
частотой w и
являются гармоническими; амплитуда и
фаза колебаний, определяемые выражениями
(147.8) и (147.9), также зависят от w.

Выведите
формулу для расчета периода: используем
соотношение F=-kx (квазиупругая сила) ,
где k — жесткость пружины. В вертикальном
положении на груз на пружине действуют
сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина
растягивается на х1,
а затем мы отклоняем его от этого
положения на х. Тогда согласно второму
закону Ньютона, учитывая знаки проекций,
получим: 
.
Но 
,
тогда: 
.

Или 
 –
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.

Выразим
ускорение:
.
Сравним полученное уравнение с уравнением
колебательного движения 
.
Видно, что 
 или 
 –
циклическая частота при колебаниях
пружинного маятника. Период
колебаний 
 или 
 (формула
Гюйгенса).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2022 года; проверки требует 1 правка.

Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Дифференциальное уравнение движения физического маятника[править | править код]

Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:

{displaystyle I=I_{0}+mh^{2}=mleft(r^{2}+h^{2}right)},

где I_0 — момент инерции относительно оси, проходящей через центр тяжести; r — эффективный радиус инерции относительно оси, проходящей через центр тяжести.

Динамическое уравнение произвольного вращения твёрдого тела:

{displaystyle I{frac {d^{2}theta }{dt^{2}}}=-M_{s}},

где M_s — суммарный момент сил, действующих на тело относительно оси вращения.

{displaystyle M_{s}=M+M_{f}},

где M — момент сил, вызванный силой тяжести; {displaystyle M_{f}} — момент сил, вызванный силами трения среды.

Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:

{displaystyle M=mghsin theta }.

Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:

I{frac {d^{2}theta }{dt^{2}}}=-mghsin theta .

Если разделить обе части уравнения на h и положить

{displaystyle lambda ={frac {r^{2}+h^{2}}{h}}={frac {r^{2}}{h}}+h},

получим:

{displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gsin theta }.

Такое уравнение аналогично уравнению колебаний математического маятника длиной lambda . Величина lambda называется приведённой длиной физического маятника.

Центр качания физического маятника. Теорема Гюйгенса[править | править код]

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии lambda от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен {displaystyle I=mlambda ^{2}}, а момент силы тяжести относительно той же оси {displaystyle -mglambda sin theta }. При этом уравнение движения не изменится.

Согласно теореме Гюйгенса,

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Вычислим приведённую длину для нового маятника:

{displaystyle lambda _{1}={frac {r^{2}}{r^{2}/h}}+{frac {r^{2}}{h}}=h+{frac {r^{2}}{h}}=lambda }.

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период колебаний физического маятника[править | править код]

Наиболее общий случай[править | править код]

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.

Для этого умножим левую {displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=lambda {frac {d}{dt}}left({frac {dtheta }{dt}}right)} и правую часть этого уравнения на dtheta. Тогда:

{displaystyle lambda {frac {dtheta }{dt}}dleft({frac {dtheta }{dt}}right)=-gsin theta ,dtheta }.

Интегрируя это уравнение, получаем:

{displaystyle lambda left({frac {dtheta }{dt}}right)^{2}=2gcos theta +C},

где C — произвольная постоянная. Её можно найти из условия, что в ситуациях, когда {displaystyle theta =pm alpha }, должно быть {displaystyle {frac {dtheta }{dt}}=0} (alpha — максимальный угол отклонения). Получаем:

{displaystyle C=-2gcos alpha .}

Подставляем и преобразовываем получившееся уравнение:

{displaystyle {frac {dtheta }{dt}}=2{sqrt {frac {g}{lambda }}}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}.}

Отделяем переменные и интегрируем это уравнение:

{displaystyle {sqrt {frac {g}{lambda }}}t=int limits _{0}^{frac {theta }{2}}{frac {dleft({frac {theta }{2}}right)}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}}}.

Удобно сделать замену переменной полагая sin {frac {theta }{2}}=sin {frac {alpha }{2}}sin varphi . Тогда искомое уравнение принимает вид:

{displaystyle t={sqrt {frac {lambda }{g}}}int limits _{0}^{varphi }{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}={sqrt {frac {lambda }{g}}}Fleft(varphi setminus alpha /2right).}

Здесь Fleft(varphi setminus alpha right) — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

{displaystyle T=4{sqrt {frac {lambda }{g}}},int limits _{0}^{pi /2}{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}=4{sqrt {frac {lambda }{g}}},Kleft(sin {frac {alpha }{2}}right).}

Здесь Kleft(sin {frac {alpha }{2}}right) — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:

{displaystyle T=2pi {sqrt {frac {lambda }{g}}}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {alpha }{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {alpha }{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {alpha }{2}}right)+dots right}.}

Период малых колебаний физического маятника[править | править код]

Если {displaystyle alpha ll 1} — случай малых максимальных угловых отклонений от равновесия {displaystyle |theta |<alpha } — то {displaystyle sin theta approx theta } так как разложение синуса в ряд Маклорена {displaystyle sin theta approx theta -theta ^{3}/3dots } и уравнения движения переходит в уравнение гармонического осциллятора без трения:

{displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gtheta .}

Период колебания маятника в этом случае:

{displaystyle T=2pi {sqrt {frac {lambda }{g}}}.}

В иной формулировке: если амплитуда колебаний alpha мала, то корень в знаменателе эллиптического интеграла приближённо равен единице. Такой интеграл легко берётся, и получается хорошо известная формула малых колебаний:

{displaystyle T=2pi {sqrt {frac {lambda }{g}}}=2pi {sqrt {frac {I}{mgh}}}.}

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.

Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):

{displaystyle Tapprox 2pi {sqrt {frac {lambda }{g}}}left(1+{frac {1}{4}}sin ^{2}left({frac {alpha }{2}}right)right)={frac {pi }{4}}{sqrt {frac {lambda }{g}}}left(9-cos {alpha }right).}

См. также[править | править код]

  • Математический маятник
  • Маятник Дубошинского

Ссылки[править | править код]

  • маятник — статья из Большой советской энциклопедии. 
Источник

1

габба­с
[215K]

4 года назад 

Если известен период колебаний математического маятника, то длину маятника можно подсчитать по известной формуле периода математического маятника Т=2*пи*корень квадратный из( L/g), где g=9,8 м/с2 – ускорение свободного падения на Земле (приблизительно). Оттуда длина маятника L = (Т^2*g)/(4*пи^2) = (1*9,8)/(4*3,14*3,14­) = 9,8/39,48 = 0,248 м или примерно 25 см.

Ответ: 25 см.

автор вопроса выбрал этот ответ лучшим

комментировать

в избранное

ссылка

отблагодарить

Источник

Добавить комментарий