Рассмотрим задачи, в которых требуется по рисунку на клетчатой бумаге найти длину медианы треугольника.
Задачи.
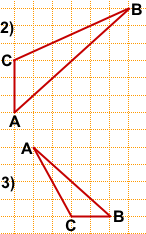
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
Решение:
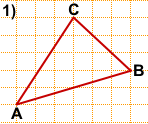
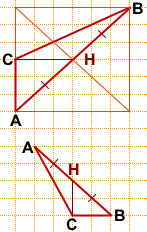
Следовательно, задачу начинаем с нахождения середины AB.
Как правило, сторона AB в таких задачах изображается не горизонтальным или вертикальным отрезком.
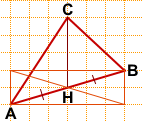
Длину медианы CH считаем по клеточкам — CH=4.
2) Аналогично предыдущей задаче, сначала найдём середину отрезка AB.
Можно достроить прямоугольник с диагональю AB, провести вторую диагональ и отметить точку H пересечения диагоналей.
Длину медианы CH находим по клеточкам:
CH=3.
3) Можно найти середину отрезка AB и без дополнительных построений.
Например, можно рассуждать так:
AH=BH как диагонали равных квадратов (со стороной 2 клетки), следовательно, точка H — середина AB, CH — медиана треугольника ABC.
CH=2.
Если медиана треугольника расположена не горизонтально либо вертикально, посчитать её длину по клеточкам не удастся.
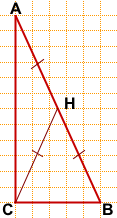
То есть для нахождения длины медианы нужно знать гипотенузу.
Длины катетов определяем по клеточкам: AC=12, BC=5.
По теореме Пифагора: AB²=AC²+BC²,
AB²=12²+5²=169, AB=13,
CH= 1/2 AB=6,5.
5) 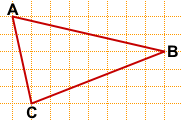
(достаточно провести вторую диагональ, прямоугольник можно не строить).
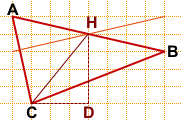
Достроим прямоугольный треугольник CHD с гипотенузой CH.
CD=3, HD=4.
CH находим по теореме Пифагора (можно также заметить, что CHD — египетский треугольник): CH=5.
Задания
Версия для печати и копирования в MS Word
Тип 18 № 311958
i
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
Спрятать решение
Решение.
Введем обозначения, как показано на рисунке и проведём медиану треугольника AH. В прямоугольном треугольнике ABC длины катетов равны 3 и 4, поэтому гипотенуза равна В прямоугольном треугольнике медиана, проведённая из прямого угла, равна половине гипотенузы, т. е. 5 : 2 = 2,5.
Ответ: 2,5.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
Чтобы найти длину медианы, выходящей из вершины B, нужно провести медиану из вершины B до середины стороны AC. Обозначим точку середины стороны AC как M. Тогда медиана, выходящая из вершины B, будет проходить через точку M и делить сторону AC пополам.
Чтобы найти координаты точки M, нужно найти среднее арифметическое координат точек A и C по каждой оси. Пусть координаты точки A равны (x₁, y₁), а координаты точки C равны (x₃, y₃). Тогда координаты точки M будут равны ((x₁+x₃)/2, (y₁+y₃)/2).
Зная координаты точки M, можно найти длину медианы, выходящей из вершины B, используя теорему Пифагора. Обозначим длину медианы, выходящей из вершины B, как MB, а длины отрезков AM и MC, как a и b соответственно. Тогда:
MB² = a² + b²
Таким образом, чтобы найти длину медианы, выходящей из вершины B, нужно найти длины отрезков AM и MC, используя формулы расстояния между точками, а затем подставить их в формулу для длины медианы.
Приведу пример нахождения длины медианы на конкретном треугольнике: пусть вершины треугольника АВС имеют координаты (0,0), (4,0) и (2,3) соответственно. Тогда середина стороны AC будет иметь координаты ((0+2)/2, (0+3)/2) = (1,5). Длина отрезка AM будет равна расстоянию между точками (0,0) и (1,5), которое можно найти с помощью формулы расстояния между точками:
a = √((1-0)² + (5-0)²) = √26/2
Аналогично, длина отрезка MC будет равна расстоянию между точками (2,3) и (1,5), которое можно найти также с помощью формулы расстояния между точками:
b = √((2-1)² + (3-5)²) = √5/2
Итак, мы нашли длины сторон треугольника: AB = 6, AC = 8 и BC = 10. Чтобы найти медиану, выходящую из вершины B, нужно найти середину стороны AC (точку M) и соединить её с вершиной B. Так как стороны треугольника параллельны осям координат на клетчатой бумаге, то точка M будет иметь координаты (5, 1). Также заметим, что точка B имеет координаты (3, 3).
Теперь мы можем найти длину медианы BM, используя теорему Пифагора для прямоугольного треугольника MBP, где P – точка пересечения медиан:
BM^2 = MP^2 + BP^2
Найдём длину MP, используя координаты точек M и B:
MP = sqrt((5-3)^2 + (1-3)^2) = sqrt(8)
Найдём длину BP, используя координаты точек B и середины стороны AC:
BP = sqrt((5-3)^2 + (3-1)^2) = sqrt(8)
Таким образом, получаем:
BM^2 = 8 + 8 = 16
BM = 4
Ответ: длина медианы, выходящей из вершины B, равна 4 клеткам.
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
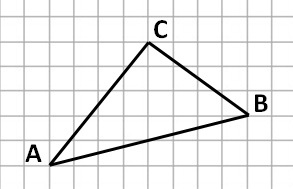
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник АВС. Найдите длину его медианы, проведенной из вершины С.
Решение:
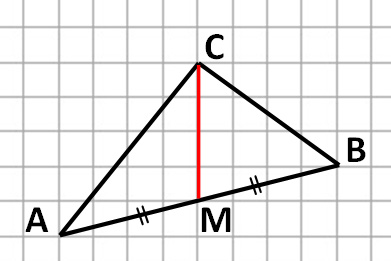
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Найдем середину стороны АВ и проведем отрезок СМ. Отрезок СМ – медиана треугольника АВС.
По клеточкам легко найти, что СМ = 4.
Ответ: 4
Понравилось? Нажмите
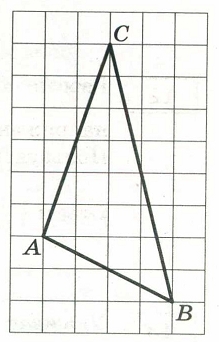
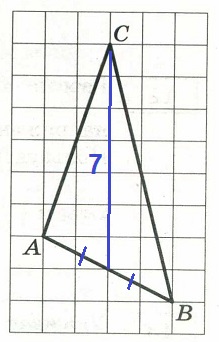
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Решение:
Медиана из вершины С будет делить противолежащую сторону АВ на две равные части:
Длинна её равна 7 клеток.
Ответ: 7.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 16
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.