Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.
Задача.
Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.
 Дано: ∆ ABC,
Дано: ∆ ABC,
BC=a, AC=b, AB=c,
сторона AC — наибольшая,
BO- медиана.
Найти: BO.
Решение:

1) На луче BO отложим отрезок OD, OD=BO.
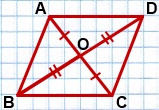
2) Проведем отрезки AD и CD.
3) Рассмотрим четырехугольник ABCD.
AO=CO (так как BO — медиана треугольника ABC по условию);
BO=DO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
4) По свойству диагоналей параллелограмма,
![]()
![]()
![]()
![]()
так как BO=1/2 BD (по построению),
![]()
Если ввести обозначение
![]()
формула для нахождения медианы треугольника по его сторонам примет вид:
![]()
Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.
Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.
Соответственно, формулы для нахождения длины медианы в этих случаях:
![]()
![]()
Приём, который применили для решения задачи — метод удвоения медианы.
Все формулы медианы треугольника
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

- Подробности
-
Автор: Administrator
-
Опубликовано: 08 октября 2011
-
Обновлено: 13 августа 2021
Медиана треугольника – это отрезок, проведенный из любой его вершины к противоположной стороне, при этом он делит ее на части равной длины. Максимальное число медиан в треугольнике – три, по количеству вершин и сторон. Зная длины всех трех сторон треугольника, можно найти его медианы. В частных случаях равнобедренного и равностороннего треугольника, очевидно, достаточно знания, соответственно, двух (не равных друг другу) и одной стороны треугольника. Медиану также можно найти и по другим данным. Вам понадобится: Длины сторон треугольника, углы между сторонами треугольника. ПОДРОБНО:
http://www.kakprosto.ru/kak-83920-kak-nayti-dlinu-mediany-v-treugolnike
Видео: http://www.uchportal.ru/video/vip/561/ogeh_gia_po_matematike/zadacha_9/podgotovka_k_ogeh_po_matematike_reshenie_zadachi_9_najdite_dlinu_mediany_treugolnika
.
Длина медианы треугольника
Медиана
Медиана — отрезок, проведенный из вершины треугольника на противоположную ей сторону и делящий ее пополам.
Медиану треугольника можно вычислить по трем его сторонам по формуле:
![]()
где M — медиана; a, b — стороны треугольника; c — третья, на которую проведена медиана.
Т.е. медиана треугольника равняется половине корня квадратного из удвоенной суммы квадратов двух сторон минус квадрат третьей стороны.
Если даны 2 стороны и угол между ними, воспользуемся формулой:
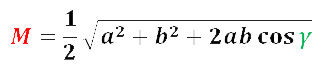
где M — медиана; a, b — стороны треугольника, γ — угол между ними.
Отсюда, медиана равна половине корня из суммы квадратов двух сторон плюс удвоенное произведение этих сторон на cos угла между ними.
Рассчитать длину медианы треугольника
Тегитреугольник
Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.
Для начала рассмотрим задачу в общем виде.
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.
AB=a, AC=b, BC=c.
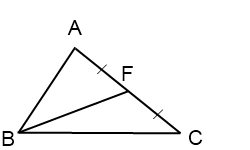
Решение.
На луче BF отложим отрезок FD, FD=BF.
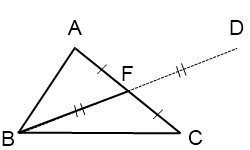
Соединим точку D с точками A и C.
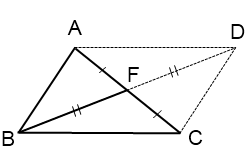
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.
Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),
BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,
![]()
Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:
![]()
Переходим к рассмотрению конкретной задачи.
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.
Решение:
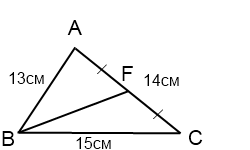
Применяя аналогичные рассуждения, получаем:
AC²+BD²=2(AB²+BC²).
Отсюда
14²+BD²=2(13²+15²)
BD²=2(169+225)-196=592
![]()
![]()
Ответ:
![]()
