Как найти длину медианы трапеции

In this tutorial video the author shows how to find the length of the median of a trapezoid. He starts to show that we first need to add the sum of the parallel sides of the trapezoid which are on the either side of the median. Now this obtained value is to be divided by two to get the length of the median. He explains that the length of the median of a trapezoid is nothing but the average of the lengths of the parallel sides of the trapezoid. If you want to learn how to find the length of the median of a trapezoid watch and learn from this tutorial.

Want to master Microsoft Excel and take your work-from-home job prospects to the next level? Jump-start your career with our Premium A-to-Z Microsoft Excel Training Bundle from the new Gadget Hacks Shop and get lifetime access to more than 40 hours of Basic to Advanced instruction on functions, formula, tools, and more.

Buy Now (97% off) >

Other worthwhile deals to check out:

• 97% off The Ultimate 2021 White Hat Hacker Certification Bundle
• 98% off The 2021 Accounting Mastery Bootcamp Bundle
• 99% off The 2021 All-in-One Data Scientist Mega Bundle
• 59% off XSplit VCam: Lifetime Subscription (Windows)
• 98% off The 2021 Premium Learn To Code Certification Bundle
• 62% off MindMaster Mind Mapping Software: Perpetual License
• 41% off NetSpot Home Wi-Fi Analyzer: Lifetime Upgrades

Диагонали трапеции

Свойства диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

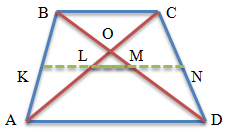
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM. 

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.

Данный отрезок параллелен основаниям трапеции.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD – BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

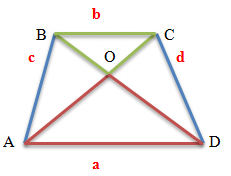
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции – являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными – они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны. 

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

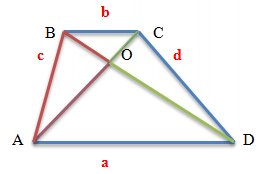
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это – треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

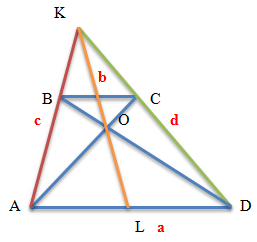
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований. 

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Свойства отрезка, соединяющего основания трапеции

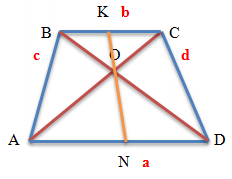
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

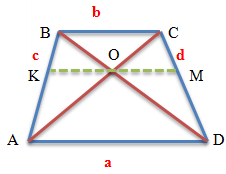
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Формулы для нахождения диагоналей трапеции

Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему “диагонали трапеции”

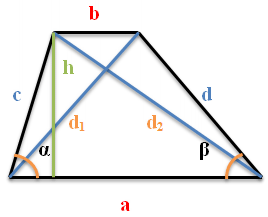
Далее, в формулах используются следующие обозначения:

a, b – основания трапеции

c, d – боковые стороны трапеции

d1 d2 – диагонали трапеции

α β – углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

 

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции,  одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

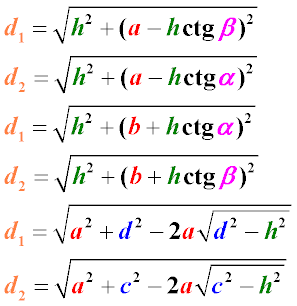
Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа – задайте вопрос на форуме.

Задача.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам – AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ: 16 см

Задача.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

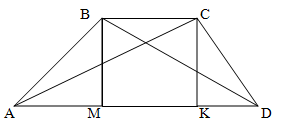
Решение.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая – то обозначим длину AM = a, длину  KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK – прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 – b

Треугольники DBM и ACK – прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

h² + (24 – a)² = (5√17)²

и

h² + (24 – b)² = 13²

Учтем, что a = 16 – b , тогда в первом уравнении

h² + (24 – 16 + b)² = 425

h²  = 425 – (8 + b)²

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 – (8 + b)² + (24 – b)²  = 169

-(64 + 16b + b)² + (24 – b)² = -256

-64 – 16b – b² + 576 – 48b + b²  = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h²  = 425 – (8 + b)² = 425 – (8 + 12)² = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

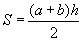, где a b – основания трапеции, h – высота трапеции

S = (24 + 8) * 5 / 2 = 80 см²

Ответ: площадь трапеции равна 80 см².

0
 

 Трапеция (задачи про основания) |

Описание курса

| Прямоугольная трапеция 

Центральная медиана трапеции Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	2D геометрия ↺
2D геометрия	Трапеция ↺
Трапеция	Центральная медиана трапеции ↺

Центральная медиана трапеции Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Длинное основание трапеции: 15 метр –> 15 метр Конверсия не требуется
Короткое основание трапеции: 5 метр –> 5 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

10 метр –> Конверсия не требуется

6 Центральная медиана трапеции Калькуляторы

3 Центральная медиана трапеции Калькуляторы

Центральная медиана трапеции формула

Центральная медиана трапеции = (Длинное основание трапеции+Короткое основание трапеции)/2

M = (B_Long+B_Short)/2

Что такое Трапеция?

Трапеция – это четырехугольник с одной парой противоположных и параллельных сторон. Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.

Неравносторонним трапеция представляет собой многоугольник с четырех сторон, два из которых расположены параллельно друг другу, и с четырьмя внутренними углами различных мер.

Ниже показан четырехугольник ABCD, где стороны AB и DC параллельны друг другу. Этого достаточно, чтобы получилась трапеция, но внутренние углы α, β, γ и δ различны, поэтому трапеция является разносторонней.

Рис. 1. Четырехугольник ABCD – трапеция по условию 1 и разносторонняя по условию 2. Источник: Ф. Сапата.

Элементы разносторонней трапеции

Вот наиболее характерные элементы:

– Основания и стороны: параллельные стороны трапеции являются ее основаниями, а две непараллельные стороны – сторонами.

У разносторонней трапеции основания бывают разной длины, в том числе и боковые. Однако разносторонняя трапеция может иметь боковую часть, равную по длине основанию.

-Средний: это сегмент, который соединяет середины боковых.

-Диагонали: диагональ трапеции – это отрезок, соединяющий две противоположные вершины. У трапеции, как и у любого четырехугольника, две диагонали. У разносторонней трапеции они разной длины.

Другие трапеции

Помимо разносторонней трапеции, есть и другие особые трапеции: правая трапеция и равнобедренная трапеция.

Трапеция – это прямоугольник, у которого один из углов прямой, а у равнобедренной трапеции стороны равной длины.

Трапециевидная форма имеет множество применений на уровне дизайна и промышленности, например, в конфигурации крыльев самолетов, форме повседневных предметов, таких как столы, спинки стульев, упаковка, кошельки, текстильные принты и многое другое.

Рис. 2. Трапециевидная форма часто встречается в конфигурации крыльев самолетов. Источник: Wikimedia Commons.

Свойства

Свойства разносторонней трапеции перечислены ниже, многие из которых распространяются на другие типы трапеций. В дальнейшем, когда говорится о «трапеции», это свойство будет применяться к любому типу, включая разносторонний.

1. Медиана трапеции, то есть отрезок, соединяющий середины ее непараллельных сторон, параллелен любому из оснований.

2.- Медиана трапеции имеет длину, которая является полусуммой длины ее оснований, и пересекает ее диагонали в средней точке.

3.- Диагонали трапеции пересекаются в точке, которая делит их на две части, пропорциональные частным оснований.

4.- Сумма квадратов диагоналей трапеции равна сумме квадратов ее сторон плюс двойное произведение ее оснований.

5.- Отрезок, соединяющий середины диагоналей, имеет длину, равную половине разности оснований.

6.- Углы, прилегающие к боковым, являются дополнительными.

7.- У разносторонней трапеции длина диагоналей разная.

8. Трапеция имеет вписанную окружность, только если сумма ее оснований равна сумме ее сторон.

9.- Если трапеция имеет вписанную окружность, то угол с вершиной в центре указанной окружности и сторонами, проходящими через концы стороны трапеции, является прямым.

10.- Разносторонняя трапеция не имеет описанной окружности, единственный тип трапеции – это равнобедренный.

Формулы и уравнения

Следующие соотношения разносторонней трапеции относятся к следующему рисунку.

1.- Если AE = ED и BF = FC → EF – AB и EF – DC.

2.- EF = (AB + DC) / 2, то есть: m = (a + c) / 2.

3. ДИ = IB = d ₁ /2 и АГ = ГХ = d ₂ /2.

4.- DJ / JB = (c / a) аналогично CJ / JA = (c / a).

Рис. 3. Медиана и диагонали разносторонней трапеции. Источник: Ф. Сапата.

5.- DB ² + AC ² = AD ² + BC ² + 2 AB ∙ DC

Эквивалентно:

d ₁ ² + d ₂ ² = d ² + b ² + 2 a ∙ c

6.- GI = (AB – DC) / 2

То есть:

п = (а – в) / 2

7.- α + δ = 180⁰ и β + γ = 180⁰

8.- Если α ≠ β ≠ γ ≠ δ, то d1 ≠ d2.

9.- На рис. 4 показана разносторонняя трапеция с вписанной окружностью, в этом случае верно следующее:

а + с = г + Ь

10.- В разносторонней трапеции ABCD с вписанной окружностью с центром O справедливо также следующее:

∡AOD = ∡BOC = 90⁰

Рис. 4. Если в трапеции проверено, что сумма ее оснований равна сумме боковых сторон, то в нее вписана окружность. Источник: Ф. Сапата.

Рост

Высота трапеции определяется как отрезок, идущий от точки основания перпендикулярно к противоположному основанию (или его продолжению).

Все высоты трапеции имеют одинаковое значение h, поэтому большую часть времени высота слова относится к ее измерению. Короче говоря, высота – это расстояние между основаниями.

Высоту h можно определить, зная длину одной стороны и одного из углов, прилегающих к этой стороне:

h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)

Медиана

Мера m медианы трапеции представляет собой полусумму оснований:

т = (а + б) / 2

Диагонали

d ₁ = √

d ₂ = √

Его также можно рассчитать, если известна только длина сторон трапеции:

d ₁ = √

d ₂ = √

периметр

Периметр – это общая длина контура, то есть сумма всех его сторон:

Р = а + б + с + г

Площадь

Площадь трапеции – это полусумма ее оснований, умноженная на ее высоту:

А = h ∙ (a + b) / 2

Его также можно вычислить, если известны медиана m и высота h:

А = м ∙ ч

Если известна только длина сторон трапеции, площадь можно определить с помощью формулы Герона для трапеции:

А = ∙ √

Где s – полупериметр: s = (a + b + c + d) / 2.

Другие соотношения для разносторонней трапеции

Пересечение медианы с диагоналями и параллели, проходящей через пересечение диагоналей, порождает другие отношения.

Рисунок 5. Другие соотношения для разносторонней трапеции. Источник: Ф. Сапата.

-Отношения для медианного EF

EF = (а + с) / 2; EG = IF = c / 2; EI = GF = a / 2

-Отношения для отрезка, параллельного основаниям KL, и проходящего через точку пересечения J диагоналей

Если KL – AB – DC с J ∈ KL, то KJ = JL = (a ∙ c) / (a ​​+ c)

Построение разносторонней трапеции с линейкой и циркулем

Для оснований длин a и c, где a> cy со сторонами длин b и d, где b> d, выполните следующие действия (см. Рисунок 6):

1.- Правилом рисуется отрезок большой AB.

2.- От A se и на AB отметьте точку P так, чтобы AP = c.

3.- С помощью циркуля с центром в P и радиусом d нарисована дуга.

4.- Центр создается в точке B с радиусом b, рисуя дугу, которая пересекает дугу, нарисованную на предыдущем шаге. Мы называем Q точкой пересечения.

Рис. 6. Построение разносторонней трапеции с учетом ее сторон. Источник: Ф. Сапата.

5.- С центром в точке A нарисуйте дугу радиуса d.

6.- С центром в Q нарисуйте дугу радиуса c, которая пересекает дугу, нарисованную на предыдущем шаге. Точку отсечки будем называть R.

7.- Отрезки BQ, QR и RA начертаны линейкой.

8.- Четырехугольник ABQR – разносторонняя трапеция, поскольку APQR – параллелограмм, что гарантирует, что AB – QR.

пример

В см указаны следующие значения длины: 7, 3, 4 и 6.

а) Определите, можно ли с их помощью построить разностороннюю трапецию, описывающую окружность.

б) Найдите периметр, площадь, длину диагоналей и высоту указанной трапеции, а также радиус вписанной окружности.

– Решение

Используя сегменты длиной 7 и 3 в качестве основания и сегменты длиной 4 и 6 в качестве сторон, можно построить разностороннюю трапецию, используя процедуру, описанную в предыдущем разделе.

Осталось проверить, есть ли у него вписанная окружность, но помня свойство (9):

Мы видим это эффективно:

7 + 3 = 4 + 6 = 10

Тогда условие существования вписанной окружности выполняется.

– Решение б

периметр

Периметр P получается сложением сторон. Так как баз в сумме дает 10, а также боковые, периметр равен:

P = 20 см

Площадь

Для определения площади, известной только ее стороны, применяется соотношение:

А = ∙ √

Где s – полупериметр:

s = (а + б + с + г) / 2.

В нашем случае полупериметр составляет s = 10 см. После подстановки соответствующих значений:

а = 7 см; б = 6 см; c = 3 см; d = 4 см

Остается:

A = √ = (5/2) √63 = 19,84 см².

Рост

Высота h связана с площадью A следующим выражением:

A = (a + c) ∙ h / 2, откуда можно получить высоту, очистив:

h = 2A / (a ​​+ c) = 2 * 19,84 / 10 = 3,988 см.

Радиус вписанной окружности

Радиус вписанной окружности равен половине высоты:

r = h / 2 = 1,984 см

Диагонали

Наконец, находим длину диагоналей:

d ₁ = √

d ₂ = √

Правильно подставляя значения, мы имеем:

d ₁ = √ = √ (36 + 21-7 (20) / 4) = √ (22)

d ₂ = √ = √ (16 + 21-7 (-20) / 4) = √ (72)

То есть: d ₁ = 4,69 см и d ₂ = 8,49 см.

Рис. 7. Чешуйчатая трапеция, отвечающая условию существования вписанной окружности. Источник: Ф. Сапата.

Упражнение решено

Определите внутренние углы трапеции с основаниями AB = a = 7, CD = c = 3 и боковыми углами BC = b = 6, DA = d = 4.

Решение

Теорема косинусов может применяться для определения углов. Например, угол ∠A = α определяется из треугольника ABD с AB = a = 7, BD = d2 = 8,49 и DA = d = 4.

Теорема косинусов, примененная к этому треугольнику, выглядит так:

d ₂ ² = a ² + d ² – 2 ∙ a ∙ d ∙ Cos (α), то есть:

72 = 49 + 16-56 ∙ Cos (α).

Решая для, получаем косинус угла α:

Cos (α) = -1/8

То есть α = ArcCos (-1/8) = 97,18⁰.

Остальные углы получаются таким же образом, их значения:

β = 41,41⁰; γ = 138,59⁰ и, наконец, δ = 82,82⁰.

Ссылки

1. CEA (2003). Элементы геометрии: с упражнениями и геометрией компаса. Медельинский университет.
2. Кампос, Ф., Сереседо, Ф.Дж. (2014). Математика 2. Grupo Editor Patria.
3. Фрид, К. (2007). Откройте для себя полигоны. Компания Benchmark Education.
4. Хендрик, В. (2013). Обобщенные многоугольники. Birkhäuser.
5. ИГЕР. (SF). Математика Первый семестр Такана. ИГЕР.
6. Геометрия младшего. (2014). Полигоны. Lulu Press, Inc.
7. Миллер, Херен и Хорнсби. (2006). Математика: рассуждение и приложения (десятое издание). Pearson Education.
8. Патиньо, М. (2006). Математика 5. Редакция Прогресо.
9. Wikipedia. Трапеция. Получено с: es.wikipedia.com

Пересечение медиан в трапеции – это точка P, в которой медианы AB и CD пересекаются. Она также является центром тяжести трапеции.

Для нахождения точки P и длины CP при заданных BC, AD и CD необходимо выполнить следующие действия:

1. Найдите среднее арифметическое BC и AD, используя формулу:

BA = (BC + AD) / 2

1. Найдите среднее арифметическое CD и AD, используя ту же формулу:

CD = (BC + AD) / 2

1. Найдите точку пересечения медиан, используя формулу:

P = (BA + CD) / 2

1. Найдите длину CP, используя формулу:

CP = √((x₂ - x₁)² + (y₂ - y₁)²)

где x₁, y₁ и x₂, y₂ – координаты точек C и P соответственно.

Пример:

Для трапеции ABCD с BC = 6, AD = 10 и CD = 8, найдите точку P и длину CP.

1. BA = (6 + 10) / 2 = 8
2. CD = (8 + 10) / 2 = 9
3. P = (8 + 9) / 2 = 8.5
4. Координаты точки C – (0,0), координаты точки P – (4.25, 4.5), поэтому

CP = √((4.25 - 0)² + (4.5 - 0)²) = √30,625 = 5,525

Таким образом, точка P равна (8.5, 4.5), а длина CP равна 5,525.